基于自适应旋转惯量的虚拟同步发电机控制策略

程启明，余德清，程尹曼，高 杰，张 宇，谭冯忍

(1. 上海电力学院 自动化工程学院，上海 200090；2. 上海电力公司 市北供电分公司，上海 200041)

0 引言

能源与环境问题的加剧，使得分布式发电DG(Distributed Generation)和微电网技术得到了广泛关注[1-3]。DG主要采用电力电子逆变器，与大电网同步发电机相比在外部有较大差异，其容量更小，输出阻抗更低，缺少系统惯性，且无法为含有DG的主动配电网提供一定质量的电压和频率支持[4-6]。

下垂控制是微电网中最常用的DG控制方法。它通过跟踪电压幅度和频率的参考信号，由逆变器调节下垂控制器的输出电压和频率，并合理分配有功和无功功率[7-9]。然而，在实施过程中下垂控制缺乏旋转惯性，使其难以提供必要的阻尼和频率支持。为了解决上述问题，虚拟同步发电机VSG(Virtual Synchronous Generator)可以模拟同步发电机的频率和电压的调节原理，以提高系统的稳定性。VSG结合了同步发电机和逆变器的特点，它非常适合用于微电网，且已被广泛接受[10 -11]。

目前VSG控制算法的研究受到广大学者的认可，但实际应用中仍然存在一些问题。在实现VSG时，它与下垂控制类似，使用有功和无功功率解耦控制，即有功功率-频率(P-f)和无功功率-电压(Q-V)下垂控制方法[12-13]。在此基础上，不少学者围绕VSG控制方法的准确性、稳定性和经济性等问题提出改进的控制方法。例如：文献[14]设计了级联的频率、相角和直流电压环控制策略，可以支持VSG在故障时为电网提供频率支撑，实现频率快速恢复，但没有考虑电压的影响；文献[15]在无功控制线路上引入了微分项，使VSG具有功率分配性能和环流抑制能力，但没有考虑微分带来的技术问题；文献[16]提出了一种虚拟电抗控制策略，通过减去虚拟的电压降，使得系统的阻抗得到改善，电抗和电阻的比值可以在一定程度上降低，但会使孤岛模式的输出电压下降；文献[17]将VSG的有功功率传输方程线性化，并引入线性控制理论，将阻尼因子与转角偏差解耦，以实现有功功率振荡抑制并保证频率稳定，但没有考虑电压的稳定性；文献[18]提出一种基于乒乓控制的转动惯量可调的VSG控制策略，可实现转动惯量对频率的动态实时跟踪，但其过程实现比较困难；文献[19]提出通过指令修正的方法以实现VSG输出电压恒定不变的控制目标，但该控制算法过程较长；文献[20]提出一种支持向量机SVM(Support Vector Machine)的转动惯量和阻尼系数自适应控制，在保证储能装置性能最好的同时，优化频率响应曲线，但该文将逆变器等效为电流源。

本文建立并研究了VSG控制的数学模型，并分析了完整的VSG有功、无功调节控制器。针对VSG中存在暂态过程长、电能质量差的缺点，提出了一种基于自适应旋转惯量的VSG技术。MATLAB/Simulink软件仿真和硬件实验的结果都验证了所提VSG控制策略的正确性与有效性。

1 传统VSG控制存在的问题

为了使DG系统具备同步发电机的特点，避免引入过多的同步发电机的瞬态变量，避免复杂的电磁耦合关系，本文采用同步发电机的经典二阶模型建立数学模型。其表达式为：

(1)

其中，J为同步电机的转动惯量；D为阻尼系数；ω0为电网同步角速度；Pm、Pe分别为机械功率、电磁功率；ω、θ分别为VSG 的角速度(即VSG的机械角速度)和虚拟功角。

图1为基于VSG的逆变器控制系统结构框图。图中，Lf为滤波电感；Cf为滤波电容；Z为负载阻抗；Zline为输电线路的阻抗；Pe、Q为计算功率；P、E分别为过程有功功率、电压；E0、Qref分别为额定电压、额定无功功率。系统主电路采用三相电压源逆变器，通过对逆变器输出接口采样获得输出功率、电压和电流。通过外环电源的作用，产生参考电压作为电流双闭环的控制信号电压。电压环路控制器采用比例积分(PI)控制以保证更好的电压跟踪。电流环采用比例(P)控制环，以电容电流作为受控变量。

图1 基于VSG的逆变器控制系统结构框图Fig.1 Structure diagram of inverter control system based on VSG

图1中的VSG算法包括虚拟调速器(频率控制器)、虚拟励磁控制器和VSG模型3个部分，分别模拟了同步发电机的调速器、励磁控制系统和同步发电机的机械特性与电气特性，通过3个控制部分的共同作用，达到模拟同步发电机运行特性的目的。其中VSG算法为该控制策略的核心，而虚拟原动机调节模块模拟了同步发电机的一次调频特性。

图2 VSG有功功率-频率控制框图Fig.2 Diagram of VSG P-f control

图2为VSG的频率控制器内部结构框图。它包括转子运动特性环节、下垂控制环节2个部分，可以输出参考电压的相位信息，使逆变器具有调频能力，从而模拟同步发电机的调速特性。

图2中有功功率-频率下垂控制的表达式为：

P=Pref+(ω0-ω)Kf

(2)

其中，Kf为有功功率下垂系数；Pref为有功功率的参考值。下垂系数的计算公式为：

(3)

其中，Pmax为分布式电源在频率下降时允许输出的最大有功功率；ωmin为微电源最大输出有功功率对应的最小频率。

当并网运行时，频率设定值与系统频率一致，下垂控制环节将失效，频率控制主要体现为转子运动特性。而当孤岛运行时，大电网不再为电网提供频率支撑，微电网频率通常会有一定的波动，此时下垂控制环节作用产生一个附加功率以减小频率波动。

图3为励磁控制器内部结构框图。图中，Kq为电压下垂控制系数；Kv为电压调节系数；Em、Eref分别为并网逆变器极端电压的真实值与指令值。励磁控制器内部结构等效于下垂控制算法中的无功功率控制回路。

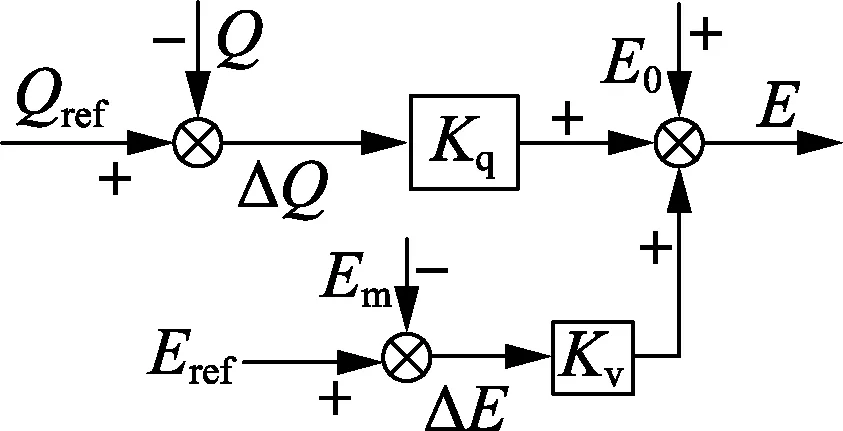
图3 VSG无功功率-电压控制框图Fig.3 Diagram of VSG Q-V control

图3中无功功率-电压控制的表达式为：

E=E0+(Qref-Q)Kq+(Eref-Em)Kv

(4)

激励控制器获得参考电压幅值信息。通过用信号合成振幅，可以产生指令电压作为电压环路的输入。在VSG控制模型虚拟励磁系统中，虚拟电动势E不仅受到无功功率调节的影响，还受到逆变器机端电压控制信号ΔE的影响。

逆变器机端电压控制信号ΔE可以等效为同步发电机的自动电压调节器AVR(Automatic Voltage Regulator)，具体表示为：

ΔE=(Eref-Em)Kv

(5)

2 基于旋转惯量的VSG自适应控制原理

VSG是在传统下垂控制的基础上加入了转子运行方程来模拟同步发电机的转子惯性与阻尼特性，相较于下垂控制，其最大的特点就是转子惯性。当进入孤岛运行模式时微电网的频率需由自身控制，此时的微电网是个独立的小系统，如果其惯性很小，那么轻微的功率波动就会引起系统显著的频率偏移，甚至可能导致整个系统的崩溃。旋转惯量J是转子惯量的代表性参数，与微电网的运行要求及微电源和储能装置的动态特性密切相关。但与同步发电机不同的是，VSG的J并非实际存在，不受硬件条件限制，取值相对灵活。

微电网在运行过程中常伴有负荷的扰动，J的取值不同，在频率动态调节过程中逆变电源将表现出不同的惯性。J的取值越小，微电网系统的惯性就越小，此时微小的负荷波动就可能引起频率的快速变化；J的取值越大，对微电网系统的频率支持作用越明显，当然，这也意味着系统的动态响应越慢，即频率到达稳定状态的时间更长。

为使VSG在给定功率变化时有更快的响应速度，结合虚拟转子惯量与功率振荡的关系，本文将频率的偏移量记为：

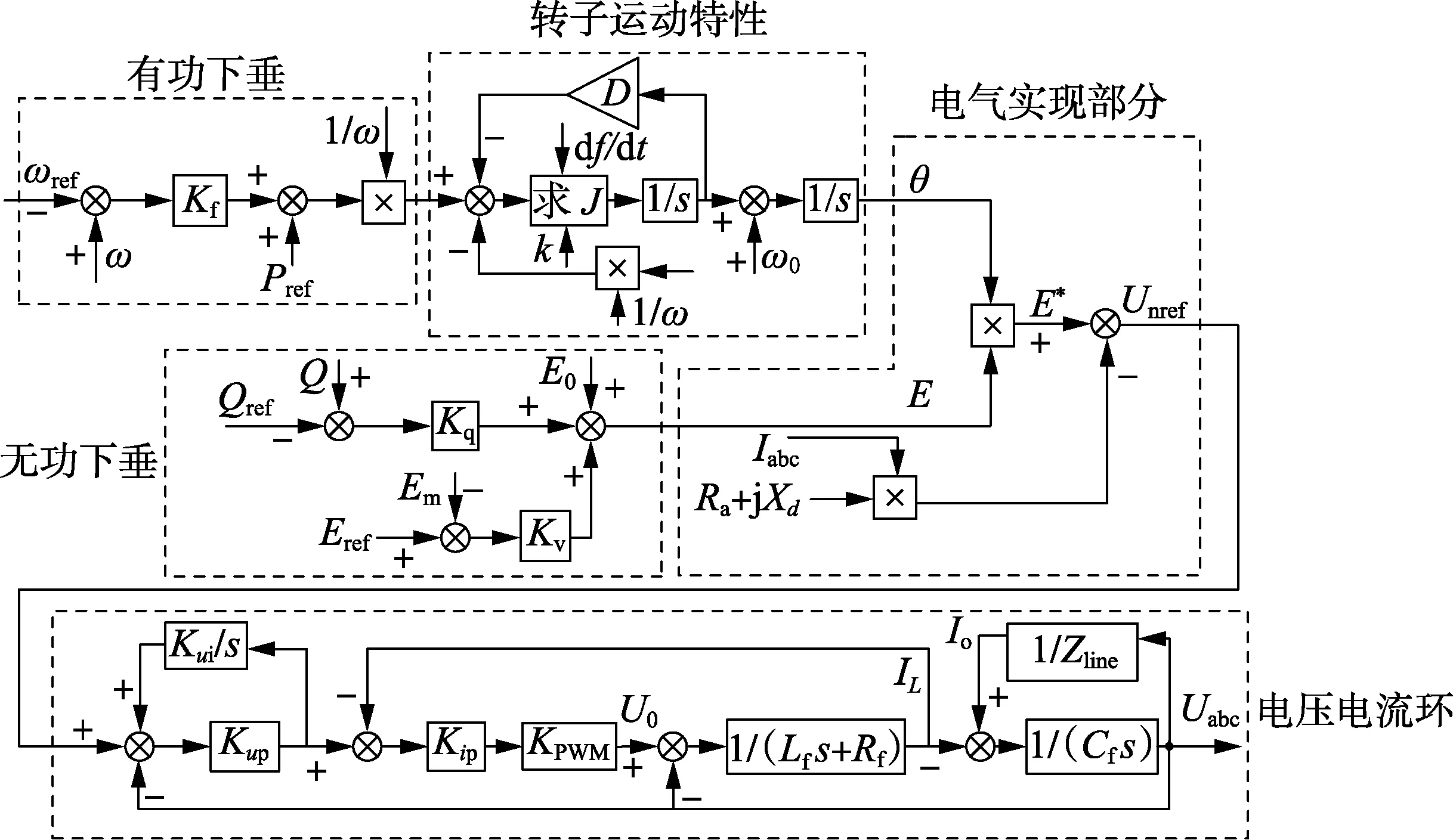
图4 基于旋转惯量的VSG控制器结构框图Fig.4 Structure diagram of VSG controller based on rotational inertia

(6)

将其作为变化量，可写出旋转惯量J的自适应函数式为：

(7)

其中，J0为VSG投入稳定运行的初始转动惯量；ωg为低通滤波器参数；k为频率变化量的限定数值，它的取值根据微电网质量要求的频率波动范围与实际运行情况决定；kf为频率跟踪系数，它决定频率误差反馈作用的强弱，即旋转惯量J跟随频率偏差变化的能力。kf的选取原则为：①当kf选取较大值时，能够根据虚拟转子频率变化率df/dt有效地改变旋转惯量J的大小，有助于减小暂态过程的超调量，但若kf取值过大，则J的值也较大，可能出现与直流侧储能装置动态特性不匹配的问题；②当kf的值选取得过小时，旋转惯量J对频率变化做出响应的能力不足，减缓频率变化的效果不佳。因此，在选取kf时，要综合考虑系统对于暂态响应超调和整体阻尼的要求。在实际工程中，kf的取值还要考虑直流侧储能装置和微电网响应特性等方面的要求。

由式(7)可知，J的自适应取值步骤为：首先判断频率的偏移量与设定数值k之间的关系，若Δf0时采用J0作为旋转惯量。

本文提出的这种新型的自适应旋转惯量方法具有以下的特点：

a. 当微电网稳定运行，系统中没有大的扰动时，采用传统的旋转惯量数值，VSG运行满足功率的要求；

b. 当系统中有较大负荷，微电源的投入或者切除时，系统的频率偏移大于设定数值，为了减少系统的频率变化带来的问题，采用新型的旋转惯量的方法；

c. 新的旋转惯量中引入了低通滤波器单元，能消除线路中的不确定因素，这种控制方法的优点是可以在负荷变化情况下保持系统频率稳定；

我省为争当农业现代化建设的排头兵，必须要建设更加完善的农业管理体系，深化农业科技体制的变革，开展高水准的农业经济管理工作可为我省农业综合改革提供动力，加快由农业大省向农业强省的转变。

d. 在新型VSG控制方法启动一定时间之后，系统趋于稳定，频率开始恢复到稳定数值，这时候频率的变化率可能发生反向变化，此时采用传统的VSG控制方法可以有效快速地使频率恢复到额定数值。

3 新型VSG控制器结构

根据前文所述，可以建立逆变器的新型VSG控制器的结构框图，如图4所示。图中，Unref和Uabc分别为定子端电压和负载电压；IL和Io分别为电感电流和负荷电流；KPWM表示逆变器的等效模型。电压外环采用PI控制器稳定负载电压，电流内环采用P控制器提高响应速度，其中Kup、Kui分别为电压环PI控制的比例系数、积分系数，Kip为电流环比例系数。新型VSG控制器包含有功下垂调节、无功下垂调节、转子运动特性、电气实现和电压电流双环控制5个模块。其中，电气实现部分包含合成电压部分和同步电机的2阶电压模型。

旋转惯量J的动态调节在转子运动特性环节中实现。在传统转子运动特性结构的基础上，本文提出的基于自适应旋转惯量的VSG控制器中增加了旋转惯量J的自适应调节控制，其具体实现过程为：① 动态获取频率的偏移量Δf和频率变化率df/dt；② 比较频率的偏移量Δf与设定值k的关系，若Δf0时，旋转惯量为J0。

同步电机的二阶模型中电压方程可以表示为：

E*=Unref+Isabc(Ra+jXd)

(8)

其中，E*、Isabc分别为励磁电动势、定子电流；Ra、Xd分别为定子电枢电阻、同步电抗。式(8)代表同步发电机定子的电气特性，与式(1)代表的转子机械特性相对应，两者综合即为同步发电机的二阶模型方程。

4 仿真分析

本文在MATLAB/Simulink软件平台上搭建了如图1所示VSG结构的仿真模型，并根据文中的分析，对自适应控制方法进行实现，由此验证本文所提VSG控制策略的正确性。仿真系统参数如下：Rf=0.1 Ω，Lf=1.5 mH，Cf=2 000F，Zline=0.1+j0.001 Ω，E0=311 V，Pset=20 kW，ω0=314 rad /s，Qset=10 kvar，ωg=3，D=20，Kup=10，Kui=100，Kip=5，fs=6 000 Hz，Kv=0.1，J0=0.5 kg·m2。

为了验证本文所提的自适应旋转惯量VSG控制策略的可行性与有效性，与传统VSG控制策略进行了仿真比较。

图5 2种控制方法下电压波形及其THDFig.5 Waveforms of voltage and THD under two control methods

图6 2种控制方法下功率波形Fig.6 Waveforms of power under two control methods

图5为传统VSG控制与自适应旋转惯量VSG控制的运行电压情况。

对比图5(a)与图5(c)可见，传统VSG控制方法的波形没有进入稳定状态下的波形失真严重，稳定以后的波峰附近亦有谐波；而自适应旋转惯量VSG控制方法整体要比传统方法更好一些，稳定状态以后的波形更接近正弦波。对比图5(b)与图5(d) 可见，传统VSG控制因采用恒定的旋转惯量存在较多的谐波，其电压总谐波畸变率THD(Total Harmonic Distortion)为7.95%，而本文提出的新型VSG控制算法的电压THD降低为4.81%。

图6为传统VSG控制与自适应旋转惯量VSG控制的有功与无功波形。由图可见，虽然改进前、后功率的稳定性都为有功40 kW、无功15 kvar，两者数值上无明显差异，但改进后的逆变器在0.04 s便进入了稳定状态，而传统的逆变器在0.08 s进入稳态，暂态时间过长。

图7为负荷阶跃变化时传统VSG控制和新型VSG控制方法下的频率波形。仿真时间为0.7 s，初始时负荷的有功功率为20 kW，无功功率为5 kvar，0.3 s后有功功率增至30 kW，无功功率增至10 kvar，0.6 s后有功功率恢复到20 kW，无功功率恢复到5 kvar。

图7 负荷阶跃变化时的频率波形对比Fig.7 Comparison of frequency under load step change

由图7可见，2种控制方法下负荷增加都会引起系统频率的下降，这与传统电网的特性相同。2种控制方法下VSG控制频率也存在差异，传统VSG控制方法下频率降为49.75 Hz，而新型VSG控制方法下系统可以更快速地进入稳定状态，在负荷增大的情况下可保证频率为49.9 Hz，更接近工频，有助于VSG的并网运行。因此，本文所提VSG控制方法在稳定系统频率方面更加表现突出，大幅提高了系统的稳定性与可靠性。

5 硬件实验

为了进一步验证本文所提VSG控制方法的正确性，在实验室现有设备的基础上制作了一台三相并网逆变器硬件样机，其控制策略分别采用本文所提的自适应旋转惯量VSG控制与传统VSG控制2种控制策略。

图8为并网逆变器的硬件结构框图。图中，主电路选用CM50MX-24A三菱IGBT模块，三相全桥逆变电路经LC滤波器接入母线；驱动电路采用HCPL-316J 驱动芯片；检测电路由电压、电流传感器和信号调理电路组成，它们主要采样逆变器的直流侧、输出侧的电压和电流、电网电压；DSP控制板中的控制芯片采用公司生产的芯片DSP28335，该芯片具有强大的事件管理能力和控制能力。

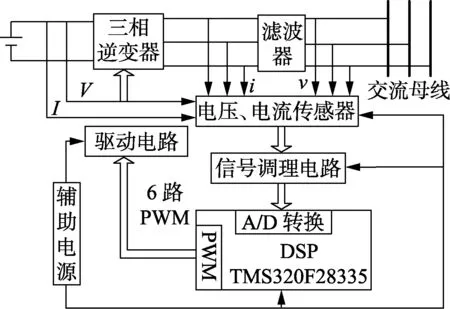
图8 并网逆变器的硬件结构框图Fig.8 Hardware structure of grid-connected inverter

硬件装置的相关参数与软件仿真数据基本一致。它们的取值分别为：直流侧电压Udc=450 V、电容Cdc=3 300F，交流滤波器的电感Lf=2 mH、电容Cf=25F，交流相电压幅值Ua=311 V，开关频率fs=6 kHz，调节周期为 0.1 ms，有功功率、无功功率的给定值分别为Pref=35 kW、Qref=0。

图9、图10分别为本文所提VSG控制和传统VSG控制方法的稳态实验波形。本文所提VSG控制的三相电流波形导入 MATLAB，通过快速傅里叶分析得到a、b、c三相电流的THD分别为2.2%、2.0%、 2.2%，功率因数为99.4%；传统VSG控制的a、b、c三相电流的THD分别为2.7%、2.3%、2.6%，功率因数为99.1%。两者稳态效果相差不多。由图可见，2种方法的波形类似，它们的三相电压和电流正弦度良好，THD为2.5%左右，功率波动不大，本文所提VSG控制指标要稍好于传统VSG控制。

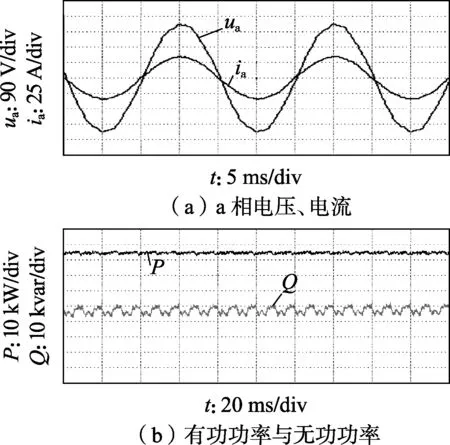
图9 本文所提VSG控制的稳态实验波形Fig.9 Steady-state experimental waveforms under proposed VSG control

图10 传统VSG控制的稳态实验波形Fig.10 Steady state experimental waveforms under traditional VSG control

图11、图12分别为有功功率给定变化时本文所提VSG控制、传统VSG控制方法的动态响应实验波形。有功功率给定由Pref=20 kW变为35 kW，无功功率给定Qref=0保持不变。由图可见，本文所提VSG控制基本无超调，但传统VSG控制存在超调，系统达到稳定的时间更长。

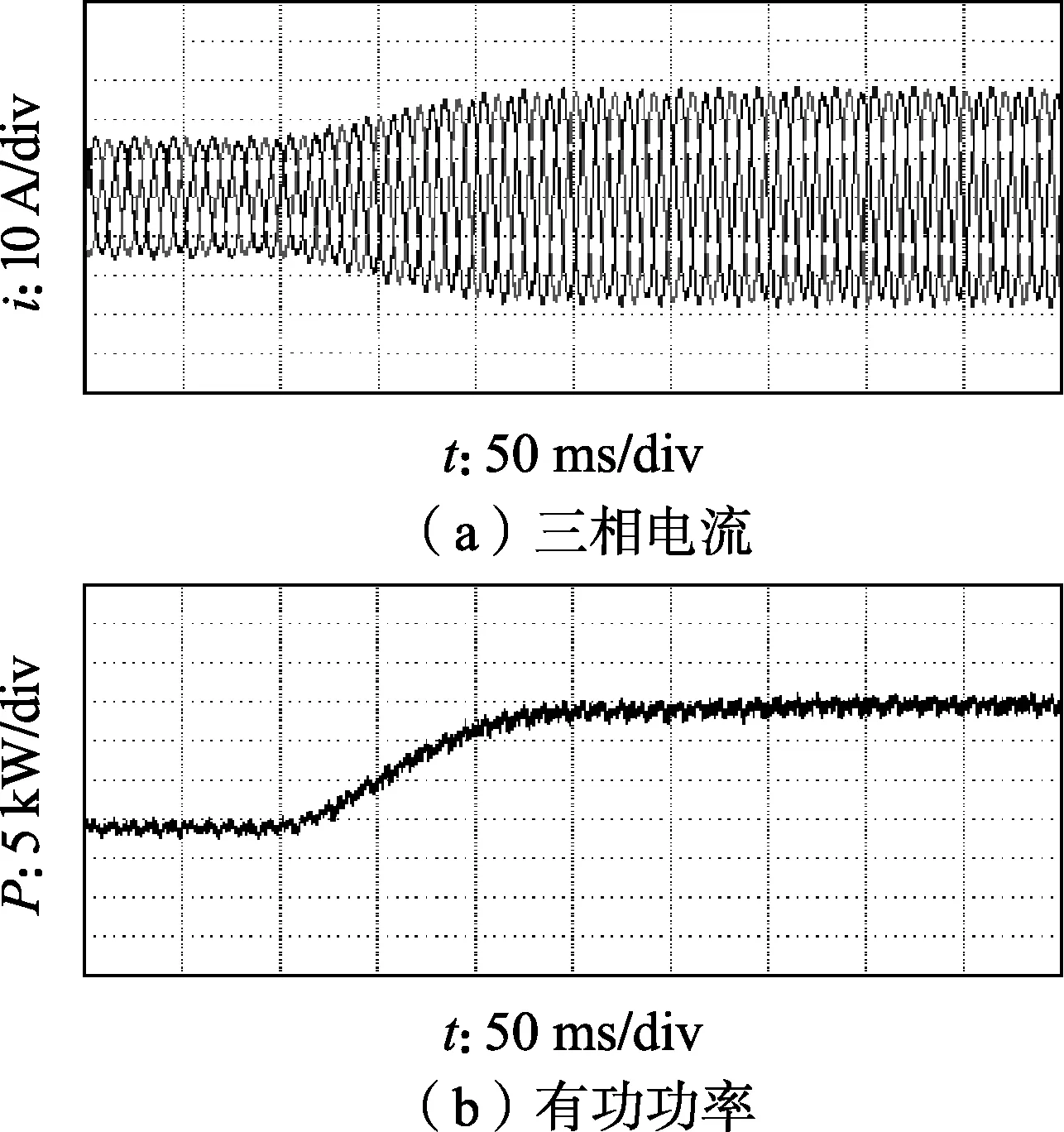
图11 有功功率给定变化时所提VSG控制的动态响应实验波形Fig.11 Experimental waveforms of dynamic response under proposed VSG control when given active power changes

图12 有功功率给定变化时传统VSG控制的动态响应实验波形Fig.12 Experimental waveforms of dynamic response under traditional VSG control when given active power changes

与有功变化情况类似，由无功变化时2种控制方法的动态响应实验波形(因篇幅限制略去)同样可见，本文所提VSG控制的超调小于传统VSG控制，且响应速度也稍快。

因此，硬件实验结果明了本文所提VSG控制的有效性和正确性。

6 结论

针对传统VSG控制中存在暂态过程长、电能质量差的缺点，本文提出了一种基于自适应旋转惯量的VSG控制策略。根据负载扰动引起的频率变化量实时动态调节旋转惯量，能够避免频率迅速上升和跌落，改善频率响应特性。当系统中有较大负荷的投入或者切除时，系统的频率偏移大于设定数值，采用新型旋转惯量控制方法可减少系统频率变化带来的问题。通过分析与实验可得出以下结论：

a. 相比于传统VSG方法，本文所提VSG控制方法缩短了系统暂态过程，系统达到稳定的时间更短；

b. 本文所提VSG控制方法抵消了系统中的大量谐波，改善了VSG的电能质量；

c. 本文所提VSG控制方法减小了输出频率下降的问题，在稳定系统频率方面表现更加突出，提高了系统频率的稳定性与可靠性。