发电机励磁与SVC的改进自适应反步无源协调控制

李啸骢，陈登义

(广西大学 广西电力系统最优化与节能技术重点实验室，广西 南宁 530004)

0 引言

目前，我国电网规模越来越庞大和复杂，输电系统已发展成大容量、远距离、超高压的输电形式。随之而来的问题是电力系统的稳定性，使用柔性交流输电(FACTS)装置是解决这个问题经济且有效的方法。其中，静止无功补偿器(SVC)具有明显的优势。其响应速度很快，损耗低，具有较好的动态和连续无功调节能力等[1]，是一种较好的FACTS装置。另外，SVC可以调节电网的无功功率，控制装设点的电压，提高电力系统的功角稳定性等[2]。发电机励磁系统作为一种传统的控制对象，在解决电网的稳定性问题中展现了突出的作用效果。因此，设计发电机励磁与SVC的协调控制器，极具研究价值。

针对发电机励磁与SVC的协调控制，国内外已取得了丰硕的成果[3-13]。文献[3]基于反馈线性化控制理论，设计了SVC与发电机励磁控制的间接自适应模糊控制器；文献[4]应用Hamilton函数方法，设计了发电机励磁与SVC的鲁棒协调控制器，可以有效地提高电力系统的暂态稳定性。除此之外，相关文献还采用了一些控制理论，包括：模糊控制[5]、自抗扰控制[6]、动态面控制[7]、人工免疫算法[8]、鲁棒控制[9]和反步法[10-13]等。由于电力系统本身就是一个非线性系统，采用非线性控制方法将最大程度地发挥其作用，因此，反步法作为一种简单且有效的非线性控制方法，已被广泛地应用于设计励磁与SVC的协调控制器中，并取得了较好的效果[10-13]。但是，“微分爆炸”问题是反步法本身存在的缺陷，已有的文献主要采用动态面控制解决这一问题。但是，动态面控制会使系统的跟踪误差只能指数收敛到有界集内，并不是全局渐近稳定的。文献[14]将反步法虚拟控制的导数看作不确定项，引入鲁棒项解决了“微分爆炸”问题，并且系统满足全局渐近稳定。因此，本文采用文献[14]的思想，引入非线性阻尼算法处理不确定项，该算法设计过程简单，而且鲁棒性强。

本文针对发电机励磁和SVC的四阶系统模型，考虑了阻尼系数的不确定，并基于自适应反步法和无源性理论，设计了一种自适应鲁棒协调控制器。对于阻尼系数的不确定性，采用浸入与不变(I & I)自适应控制，设计其自适应估计律，增强其自适应能力。并且，引入非线性阻尼算法对反步法进行改进，以解决“微分爆炸”问题。

1 无源性设计方法

针对非线性系统，有：

(1)

其中，x∈Rn；u∈Rm；f(x)、g(x)和h(x)为光滑函数向量。

对于已知的供给率s(u,y)，如果存在半正定的函数V(x)，在∀t≥0的情况下，有耗散不等式(2)成立，当供给率s(u,y)=yTu时，称非线性系统(式(1))为无源系统。

(2)

其中，V(x)为能量存储函数。

如果存在能量存储函数V(x)和正定函数D(x)，满足：

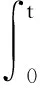
(3)

且对于所有的u∈Rm，当t≥0时式(3)都成立，则系统(式(1))是严格无源的。

根据文献[10]，当双输入单输出系统(u,y)的相对阶为1时，式(1)可转化为：

(4)

取式(4)的控制律为：

(5)

另外，系统的李雅普诺夫函数W(z)满足：

(6)

其中，σ(·)为K类函数。

取能量存储函数V(x)为：

V=W(z)+0.5y2

(7)

2 系统模型的建立

将电网等效为单机无穷大系统，在输电线路中安装SVC，如图1所示。

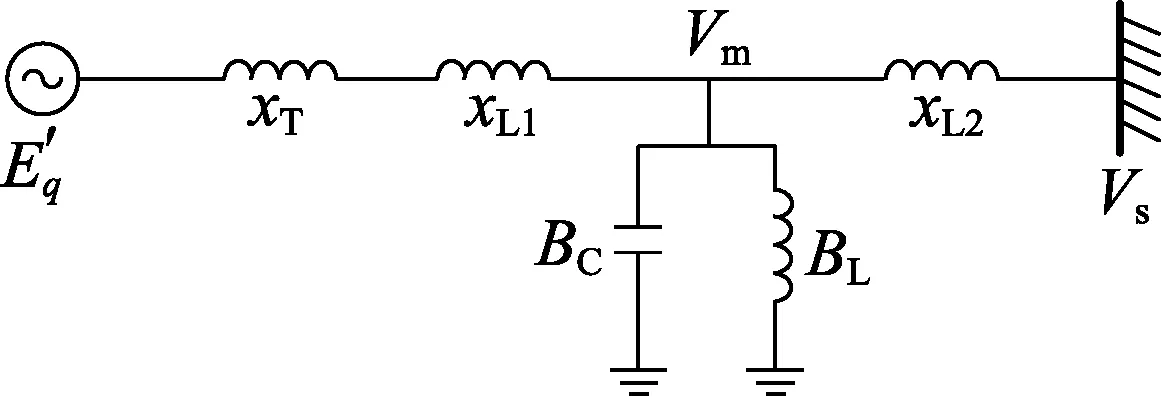
图1 含SVC的单机无穷大系统Fig.1 Single-machine infinite-bus system with SVC

对于发电机励磁系统，做如下假设：发电机选用隐极机，采用三阶模型；忽略调速器的作用；不考虑定子回路电阻和转子阻尼绕组的影响；SVC采用一阶惯性方程式表示。故图1中系统的状态方程为：

(8)

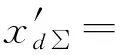
xd∑=x1∑+xL2+x1∑xL2(BL-BC)=x1∑+xL2+

x1∑xL2(ΔBL+BL0-BC)

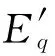
(9)

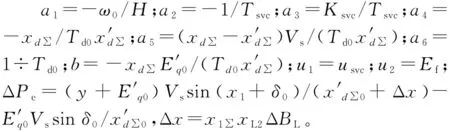
为了方便设计控制器，将式(9)表示为矩阵形式：

(10)

3 控制器的设计

发电机励磁与SVC协调控制器的设计过程主要如下：在无励磁控制的条件下，采用结合了I & I自适应控制和非线性阻尼算法的改进自适应反步法，设计SVC的控制律u1；应用无源性理论，设计励磁控制律u2。

3.1 设计SVC的控制律u1

由式(9)可知，无励磁控制的状态方程为：

(11)

首先，根据I & I自适应控制方法，设计自适应估计律，其过程如下。

取估计误差为：

(12)

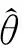
对式(12)求导，可得：

(13)

取参数θ的自适应估计律为：

(14)

将式(14)代入式(13)，可得：

(15)

根据文献[15]，取λ(x1,x2)为：

(16)

将式(16)代入式(15)，可得：

(17)

然后，采用改进反步法设计SVC的控制律，设计过程如下。

a. 定义e1=x1，e2=x2-x2d，其中x2d为虚拟控制量。

对e1求导，可得：

(18)

本文借鉴文献[14]的思想，将e2看作不确定项，并做假设1如下：令|e2|≤μ1，其中μ1为待设计的正常数。

应用非线性阻尼算法，设计x2d为：

(19)

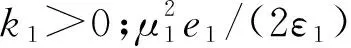
(20)

对V1求导，可得：

(21)

b. 对e2求导，可得：

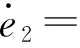
(22)

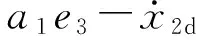
应用非线性阻尼算法，设计ΔPe1d为：

(23)

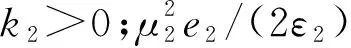
取式(11)前两阶的Lyapunov函数为：

(24)

对V2求导，可得：

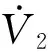
(25)

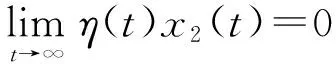
当满足|e2|≥2ε2/μ2时，有：

(26)

c. 定义e3=ΔPe1-ΔPe1d，其中ΔPe1d为虚拟控制量。

对e3求导，可得：

(27)

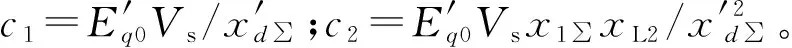
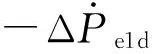
应用非线性阻尼算法，设计u1为：

(28)

取式(11)的全局Lyapunov函数为：

(29)

对V3求导，可得：

(30)

当满足|e3|≥2ε3/μ3时，有：

(31)

3.2 设计发电机励磁的控制律u2

令W(e)=V3，取整个系统的存储函数为：

V=W(e)+0.5y2

(32)

根据式(5)，设计u2为：

(33)

对V求导，可得：

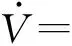
a4y2+vy≤vy

(34)

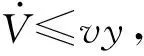
综上所述，发电机励磁与SVC协调控制器的控制律为：

(35)

因此，系统(式(9))的闭环误差系统为：

(36)

需要注意的是，参数θ的自适应估计律的设计和反步法是分开的，而且不用构造Lyapunov函数，引入了函数λ(x1,x2)，突破了确定性-等价性原则；与反步法相比，在控制器的设计过程中，本文的改进反步法没有了耦合项，一定程度上解决了“微分爆炸”问题。

4 仿真分析

4.1 小干扰情况下的仿真分析

t=0时，发电机功角偏离平衡点3°，转速ω、电磁功率Pe、SVC安装处电压Vm、机端电压Vt的仿真结果如图2所示。图中，实线为本文所提改进自适应反步无源协调IABPC(Improved Adaptive Backstepping Passive Coordinated)控制下的仿真结果，虚线为文献[9]采用的自适应反步无源协调ABPC(Adaptive Backstepping Passive Coordinated)控制下的仿真结果;电磁功率Pe、SVC安装处电压Vm、机端电压Vt均为标幺值，后同。

图2 小干扰时仿真结果Fig.2 Simulative results under small disturbance

由图2可以看出，当系统受到小干扰时，相比于ABPC控制方法，采用IABPC控制方法可以快速地平息功率振荡，恢复稳定的时间大约缩短了60%，证明了IABPC控制器具有较好的静态性能。

4.2 大干扰情况下的仿真分析

t=0.3 s时，变压器高压侧母线出口处发生三相短路，0.45 s时切除故障。仿真结果如图3所示。由图3可以看出，当系统受到大扰动时，采用IABPC控制方法可以快速地镇定受扰系统，使其回到稳定状态，收敛速度快，振荡范围和幅度都小，提高了系统的暂态稳定性，其效果优于ABPC控制方法。

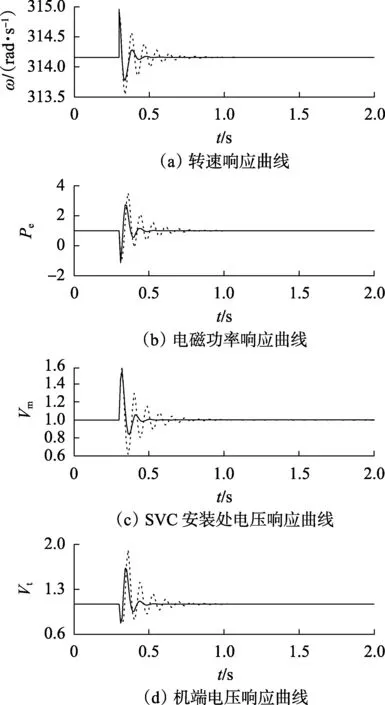
图3 大干扰时仿真结果Fig.3 Simulative results under large disturbance

图4 参数θ估计性能对比Fig.4 Comparison of estimation performance of parameter θ

为了验证本文所设计的控制器具有较强的自适应能力，将浸入与不变自适应反步I & IAB(Immersion and Invariant Adaptive Backstepping)法和自适应反步AB(Adaptive Backstepping)法进行对比分析，仿真结果如图4所示。在仿真中，取阻尼系数D=1，则参数θ=-0.143。由图4可知，相比于AB法，采用I & IAB法设计的自适应估计律更接近设定值，具有更强的自适应能力。

5 结论

本文针对含不确定参数的发电机励磁与SVC协调系统，采用I & I自适应控制、改进反步法和无源性理论，设计了一种改进自适应鲁棒协调控制器。将虚拟控制量的导数处理为不确定项，应用非线性阻尼算法，解决了反步法的“微分爆炸”问题。另外，自适应估计律的设计和反步法是独立的，并且无需构造Lyapunov函数，突破了确定性-等价性原则。基于MATLAB的仿真结果表明，本文的发电机励磁与SVC非线性协调控制器具有良好的暂态性能，改善了电力系统的稳定性。