由井-含水层系统对地震波的响应估计BKu系数

赵 頔，史浙明，王广才，周平根，孙小龙，丁 谋

(1.中国地质大学(北京)生物地质与环境地质国家重点实验室， 北京 100083；2.中国地质大学(北京)地下水循环与环境演化教育部重点实验室， 北京 100083；3.中国地质大学(北京)水资源与环境学院， 北京 100083；4.中国地质环境监测院， 北京 100081；5.中国地震局地壳应力研究所(地壳动力学重点实验室)， 北京 100085；6. 天津城建大学环境与市政工程学院， 天津 300384)

地震是一种极常见的自然地理灾害，多发于板块边缘和板块内部的构造活动带，由于能量积累而产生，可以改变地质构造和地下水的运动状态。地壳中普遍存在的地下水，形成于一定封闭条件承压含水层时，可以起到灵敏测压计的作用，能够放大井-含水层系统压力波动的影响，客观地反映地壳中应力应变状态的变化情况。一旦受到外力干扰，含水层孔隙的收缩和膨胀能够引起含水层孔隙压力ΔP的变化，并通过渗透水流传递静水压力以井水位动态表现。井水微动态的改变相对迅速，微小的应力应变改变都会在封闭性较好的承压含水层井孔位上清晰、明显地反应[1]。通过监测地震地下流体动态变化获得水文地质、物理应力应变和水化学等多方面的地球参数，对于地震的预报工作尤其对地壳活动特征、地壳内孔隙压力和体应力、偏应力等的应力分布、地下水径流以及含水层性质等方面的研究提供了非常重要的依据。对于许多地质工程应用来说，理解地震导致的地下水位变化机制对于地下水资源评价与管理，滑坡的稳定性评估，采矿设施的稳定性，评价水库诱发地震等方面至关重要[2]。

井水位对气压，固体潮和地震波的响应表明井-含水层系统对地壳应力具有灵敏的响应，同时这些响应隐含着含水层的重要信息，提供了获取含水层特性的方法[3～4]，因此很多学者利用地震波与水震波的关系估算岩石的水力性质。Cooper等探究了敞口自流井水位波动与地震波的幅频特征，从理论推导和频谱分析两方面研究含水层特性[5]；Kano研究了封闭井中水位对地震波响应的频率范围，提供了利用水震波与地震波关系估算Skempton常数的方法[1]；晏锐等分析了水位与体应变之间的变化关系，计算出水位与体应变之间的敏感系数[6]。在以往的研究中，许多地震工作者尝试应用线性孔隙弹性理论解释井-含水层系统中井水位与应力应变的相关关系，认为地震波通过时含水层的应力应变变化会导致孔隙压力改变，引起井-含水层间的水流运动，从而导致井水量发生变化，表现为井水位的升高或降低[1,7]。其中多数研究认为水位只响应于体应变[1,8]。众所周知，由于Rayleigh波和P波影响使得含水层扩张和收缩，然而最近研究表明由于岩石的各向异性，S和Love波对井水位也会产生影响[5,9～10]。前人实验研究成果表明，体应力和偏应力会对孔隙压力造成不同程度的影响[11～12]。因此，孔隙压力的影响因素及岩石线弹性系数BKu的计算方法有待进一步研究。

本文以线性孔隙弹性理论为基础，探究了井-含水层系统孔隙压力变化与体应变和偏应变之间的数学表达式，通过对2011年3月11日日本Mw9.0地震引起的昌平地下水观测井实测水位变化与曲线拟合得到的计算值对比，给出了一种求解岩石线弹性系数BKu的方法。与潮汐分析方法对比，验证了由地震方法推算的岩石弹性特性代表实际的含水层特征。

1 昌平井观测概况

北京昌平地震台位于北京市昌平县境内，处于北东走向的南口-山前活动断裂与北西走向的南口-孙河活动断裂交汇部位以东7.5 km处(图1)。地表为第四系沉积层，是新构造活动的复杂地带，同时也是前兆观测的灵敏点[13]。

昌平地下水观测井为中国地震局于1986年为了观测水位而设置的钻井，井孔柱状图见图1。0～14.3 m 深处井孔直径为170 mm，安装168 mm套管，14.3～90.1 m深度井孔直径为150 mm。昌平井含水层位于北京温榆河冲洪积平原含水层系统的下部，主要由雾迷山组白云质灰岩组成，主要含水层厚度为30 m，在观测井70～100 m深度钻核为碎片状态。观测井由黄褐色砂质黏土、残坡积灰岩和灰黑色致密坚硬块状硅化灰岩组成，硅化灰岩岩石破碎，节理发育，岩石中燧石条带明显。按施工设计，该井水位的变化为下部含水组的压力变化导致[6]。所取岩芯均为碎块，一般约为5 cm。岩层倾斜约45°，在43.35～44.41 m处有约1.06 m厚度溶洞，固结水泥，由超声波井下电视图可以观测到57.20～59.70 m处岩石完整，在70～101 m处节理裂隙及其发育。

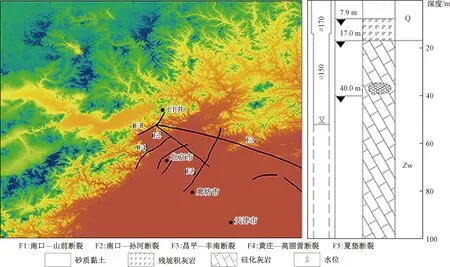
图1 昌平井构造环境及其井孔结构图Fig.1 Structural environment and well hole structure of the Changping well

2001年9月我国地震台网完成了数字化改造，水位观测采用数字化自动观测，实现了分钟值采样和数据自动传输的功能。2010年投入使用LN-3类型水位传感器观测昌平井水位，测量精度为±0.2%，稳定性±0.25%，仪器分辨率<1 mm，采集数据样品率50 Hz。

2 昌平井井储效应的校正

昌平地下水观测井成功记录到了由日本地震造成的水位波动，同时位于昌平井东部1.2 km的十三陵地震台由BBVS-120类型地震仪记录到了地震波波形的变化(图2)，震中距为2 283 km。本研究将水位数据与3个方向地震波波形数据进行对比分析，当P波和S波到达时，水位波动仅有轻微加强趋势，而Love和Rayleigh波作用阶段，水位波动强烈，因此日本地震引起的水位改变主要受到了面波的影响。地震波传播方向由东往西，意味着十三陵地震台记录到的地震波东西和垂直方向速度大于南北方向的传播速度[14]。

图2 2011-03-11 13:45～14:10 日本Mw9.0地震波速度与测量井水位响应(a)径向速度；(b)横向速度；(c)垂向速度；(d)水位变化Fig.2 compare of groundwater levels and three component seismic velocity waveforms recorded at SSL during the period from 13:45 to 14:10 (GMT+8:00) on 11 March 2011 to the Mw9.0 Tohoku earthquake. (a) Radial; (b) Transversal; (c) Vertical component of seismogram;(d) Groundwclter level changes recorded at the Changping well

地震波到达前13:45～13:50的水位和地震波形特征判断为非干扰阶段，P、S波(13:51～13:56)和Love、Rayleigh波(13:56～14:02)时间段作为干扰阶段。Love波相存在更大的横向速度，分散性较小，而Rayleigh波存在更大的径向和垂向速度并且有明显的发散，面波这一传播特点为此次研究提供了科学依据和重要参考[15]。本研究分析重点为地震波的体应力和偏应力对岩层孔隙压力造成不同程度的影响。由于P、S和Love、Rayleigh波相特征不同，因此体应力和偏应力可以分开研究。图2显示地震波速度和水位变化之间具有相似性。Shalev等人曾利用位于以色列死海断裂带的Meizar1(敞口井)和Meizar2(封闭井)对2015年Nepal地震引起的水位震荡进行对比研究[16]，两口井具有相同含水层条件，相距3 km，由水位的时间序列可以看出相对于同一条件下的封闭井，敞口井Meizar1的水位有明显的衰减，衰减因子为12，这种衰减是由于存在井孔储积效应而形成。本研究的目的是量化水位变化与地震波速度关系。由于昌平井为敞口自流井，因此孔隙压力受到井储效应的影响，首先校正井孔储积效应。Liu提供了校正井孔储积效应的方法[17]，Cooper也对井储进行了研究并提出了计算公式[18]：

He=Hw+3/8d

(1)

aw=rw(ωS/T)1/2

(2)

ωw=(g/He)1/2

(3)

式中：x0/h0——地震波的周期作用；

Ker、Kei——0阶Kelvin作用；

g——重力加速度；

He——井水有效高度；

Hw——上层含水层的水体高度；

d——含水层厚度；

rw——井孔半径;

aw——与井-含水层系统和地震波有关的参数；

S——储水系数；

T——导水系数；

ω——地震波周期。

昌平井的衰减因子为38.99，对水位数据校正，排除井储影响。校正井孔储积效应后可得到敞口井真实的水位变化与地震波速度关系的耦合。

3 孔隙压力与体应力、偏应力的耦合

井中水位响应于地震波的振幅取决于地震波特征，含水层特性和井孔的几何特性。本文从井-含水层系统对地震波的多孔性响应特征角度重点研究。Skempton认为偏应力也能影响孔隙压力[18]， Holtz和Kovacs阐释了三维空间内偏应力和孔隙压力的相关关系[19]：

(4)

式中：ΔPf——孔隙压力变化；

A和B——Skempton系数；

σm——平均应力；

σd——单轴偏应力且σ1=σ2[20]，对于地震波此应力应变关系应简化为二维空间关系：

(5)

式中：Ku——不排水条件下的体积模数；

εν——体应变；

N——剪应力耦合系数；

μ——剪力模数；

εd——偏应变。

3.1 潮汐分析估算BKu

封闭性良好的井-含水层系统中，外力导致含水层孔隙介质发生形变，井水位随之改变。在多孔介质中孔隙压力和体应变的关系可表达为：

p=BKuε

(6)

式中：p——孔隙压力；

BKu——潮汐系数；

ε——体应变。

井-含水层系统在潮汐应变周期性作用下，含水层中的孔隙压力会相应产生周期性的变化，由于含水层与井孔之间发生水量交换，使得井中水位产生与潮汐变化类似的状态：

p=ρgh

(7)

联立式(6)、(7)得到：

(8)

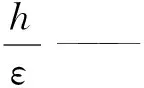
ρ——水的密度ρ=1 g/cm3；

BKu——潮汐系数，是表征岩石弹性大小的参数量。

B是基于孔弹性理论的重要参数，在0～1范围内，无量纲，与岩石岩性相关，由水位变化与张力关系计算，Ku为正值。

3.2 地震方法估算BKu

3.2.1面波应力组成

Love波和Rayleigh波在地球的表面传播，在径向和垂直方向上均有速度，横向应力εTT为0。

σzz=λeεv+2μeεzz+BKuαBεv=0

(9)

σRz=2μeεRZ=0

(10)

σTz=2μeεTZ=0

(11)

εv=εRR+εTT+εZZ

(12)

其中，λe、μe为有效Lame模数，αB为Biot系数。利用εTT=0，联立式(9)和(12)得：

(13)

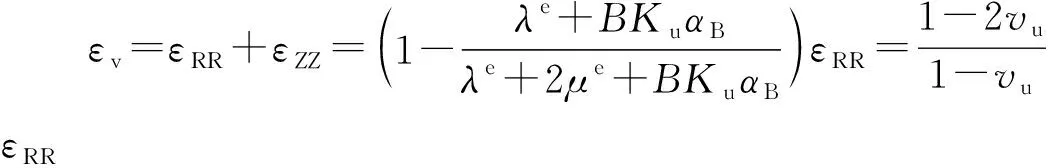
(14)

偏应力可由地震波速度表示：

(15)

(16)

εRT=εd

(17)

式中：uR和vR——地震波径向速度；

uT和vT——横向速度；

VR——Rayleigh波速度为3.5 km/s；

VL——Love波速度3 km/s。

将式(15)带入式(14)得：

(18)

联立式(5)、(16)、(17)、(18)可获得孔隙压力与体应力和偏应力的相关关系计算式：

(19)

当只考虑体应力对孔隙压力的影响时：

(20)

当只考虑偏应力对孔隙压力的影响时：

(21)

3.2.2体波应力组成

体应力可由地震波速度表示：

(22)

(23)

其中，VP,S为P波速2.5 km/s，S波速1.5 km/s。P、S波孔隙压力与体应力和偏应力的相关关系为：

(24)

4 结果讨论

4.1 潮汐分析

4.2 地震分析

4.2.1Love和Rayleigh波

选择Love波和Rayleigh波出现的时间段13:56～14:02作为研究对象，对日本地震引起的昌平地下水观测井校正井储效应后的实际水位变化与计算值曲线拟合，拟合结果见图3。

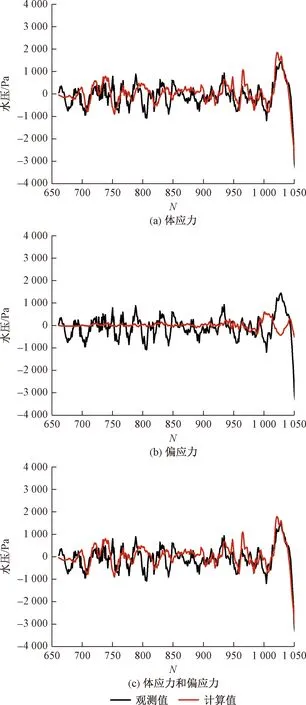
图3 体应力、偏应力、体应力和偏应力对孔隙压力的影响Fig.3 Assuming the volumetric strain(a), assuming only deviatoric stress(b) and assuming both volumetric strain and deviatoric stress(c)

4.2.2P和S波

同时考虑P和S波体应力和偏应力对孔隙压力的影响结果见图4。

图4 体波体应力和偏应力对孔隙压力的影响Fig.4 Assuming both volumetric strain and the deviatoric stress

4.3 潮汐分析与地震分析结果对比

潮汐分析得到BKu=6.42 GPa(地震前)及BKu=7.42 GPa(地震后)。地震分析中，综合考虑体应力和偏应力对孔隙压力的共同影响，利用Love和Rayleigh波为研究对象，得到BKu=3.32 GPa。潮汐分析与地震分析结果对比，肯定了由井-含水层系统对地震波的响应估计BKu系数方法的可行性。昌平井以灰岩为主，灰岩实验室参数测量结果进一步验证了地震方法的可行性[21]。

5 结论

本研究以线性孔隙弹性理论为基础，探究了井-含水层系统孔隙压力变化与体应变和偏应变之间的数学关系，通过对2011年3月11日日本Mw9.0地震引起的昌平地下水观测井实测水位变化与曲线拟合得到的计算值对比，得到以下几点认识：

(1)对于敞口井，井孔储积效应的存在会削弱水位和水压，导致测量结果偏小。在研究前校正井孔储积效应时，本文提供了一种较为科学的方法进行校正。

(2)当同时考虑体应力和偏应力对孔隙压力的影响时，相关系数最高，表明孔隙压力受到体应力和偏应力的共同影响。