Ratio Between Sensitive Strength to Light Information and Coupling Strength A ff ects Entrainment Range of Suprachiasmatic Nucleus∗
Chang-Gui Gu(顾长贵), Hui-Jie Yang(杨会杰),and Man Wang(王曼)
1Business School,University of Shanghai for Science and Technology,Shanghai 200093,China
2School of Foreign Languages and Literature,Shandong University,Jinan 250100,China
AbstractThe suprachiasmatic nucleus(SCN),an endogenous clock in the brain of the mammals,regulates the physiological and behavioral activities according to the natural 24 h light-darkness cycle.Animals can also entrain themselves to non 24 h light-darkness cycles.The range of the periods which the animal can entrain to is called entrainment range.Previous studies have found that the entrainment range depends on the coupling strength and the sensitive strength to the light for the SCN neurons.However,the effect of the interplay between these two strengths on the entrainment range has not been examined.In the present study,we examine the effect of the ratio of the sensitive strength to the coupling strength on the entrainment range.We find that there is a parabolic-like relationship between the entrainment range and the ratio,and the largest entrainment range is obtained with a suitable ratio.Interestingly,the value of this suitable ratio is related to the comparison in the intrinsic amplitudes between the light information sensitive neurons and the light information insensitive neurons.Our finding will shed light on the interplay between the sensitive strength to the light information and the coupling strength,and the understanding for the diversity of the entrainment range among various species.
Key words:biological rhythms,neuronal network,nonlinear dynamics,entrainment range
1 Introduction
The living beings on earth have evolved to be entrained to the natural 24 h light-dark cycle.The physiological or behavioral activities of the living beings are thus perfectly accustomed to the light-darkness cycle.[1−3]Interestingly,the living beings can also entrain themselves to the external cycles with artificial periods.For example,Rattus norvegicus can be entrained to external cycles with periods ranging from 23.5 h(lower limit of entrainment,LLE)to 28.5 h(higher limit of entrainment,HLE),Arivicanthis niloticus from 22.5 h to 25.5 h,and humans from 20.5 h to 29.0 h.[3−5]The range of the periods that the living beings can be entrained to,i.e.,from the LLE to the ULE,is called the entrainment range.The entrainment range is distinctive among species.
The entrainment of living beings is regulated by an endogenous clock,i.e.the suprachiasmatic nucleus(SCN),which is located above the optic chiasm in mammals.[1−3]The SCN is a network,which is composed of 20,000 selfoscillating neurons.[6−7]These neurons can be divided into two groups functionally and physically,including one named the ventrolateral part of the SCN(VL)and the other the dorsomedial part of the SCN(DM).The VL is composed of about 25%SCN neurons,and is sensitive to the light information from the retina;and the DM contains the rest 75%SCN neurons and is insensitive to the light information,which is coupled to the VL.[8−10]The VL and the DM are also distinctive in the neurotransmitters,such as vasoactive intestinal polypeptide(VIP)in the VL,arganine vasopressin(AVP)in the DMs.[11−13]These neurotransmitters play key roles in the coupling of the neurons within and between group.Additionally,there are debates about whether the amplitudes of the neurons are related to regions.The neurons of the VL and the DM are found to differ in the amplitudes,i.e.,the amplitudes of the VL neurons are smaller than the DM neurons.[14−16]However,recent findings showed that the amplitudes are not related to specific regions.[17−19]
A question is raised about that how the SCN network determines the entrainment range.Previous studies found that the entrainment range is in fluenced by the sensitivity to light information and the cellular coupling for the SCN neurons,respectively.[4,20−23]Specially,with the increase of the sensitivity strength,the entrainment range also increases.[20−21]Nevertheless,the relationship between the entrainment range and the coupling strength is not monotonous but is parabolic-like,and the largest entrainment range can be obtained with a suitable coupling strength.[22−23]So far,however,no study has taken into account the effects of the interplay between the sensitivity and the coupling strength on the entrainment range.
In this study,we will examine the effects of the interplay on the entrainment range of the SCN based on a Poincaré model.A key parameter is introduced to represent the interplay,i.e.,the ratio of the sensitivity strength to the coupling strength.The rest of this article is organized as follows.In Sec.2,the Poincaré model is introduced to mimic the SCN network.Then,the effect of the ratio on the entrainment range is examined by numerical simulations in Sec.3.In Sec.4,theoretical analysis is given to confirm the simulation results.Finally,in Sec.5,the conclusion and discussion are presented.
2 Description of the Poincaré Model
The Poincaré model is often used to mimic the coupled SCN oscillators when they are exposed to an artificial T light-dark cycle.[4,21−24]Each neuronal oscillator has two variables,x and y.The oscillators are coupled through a mean field F,which is the mean of x from all oscillators.In the present study,a key parameter ρ is introduced to describe the ratio between the sensitive strength Kfto light information and the cellular coupling strength g(ρ=Kf/g).The model composed of N oscillators is presented as follows:

where the parameters γ,ci,and τ represent the relaxation parameter,intrinsic amplitude,and intrinsic period of the individual oscillator,respectively.The neuronal oscillators are coupled through the mean field term gF.The parameter riis the amplitude of ithoscillator which reads:

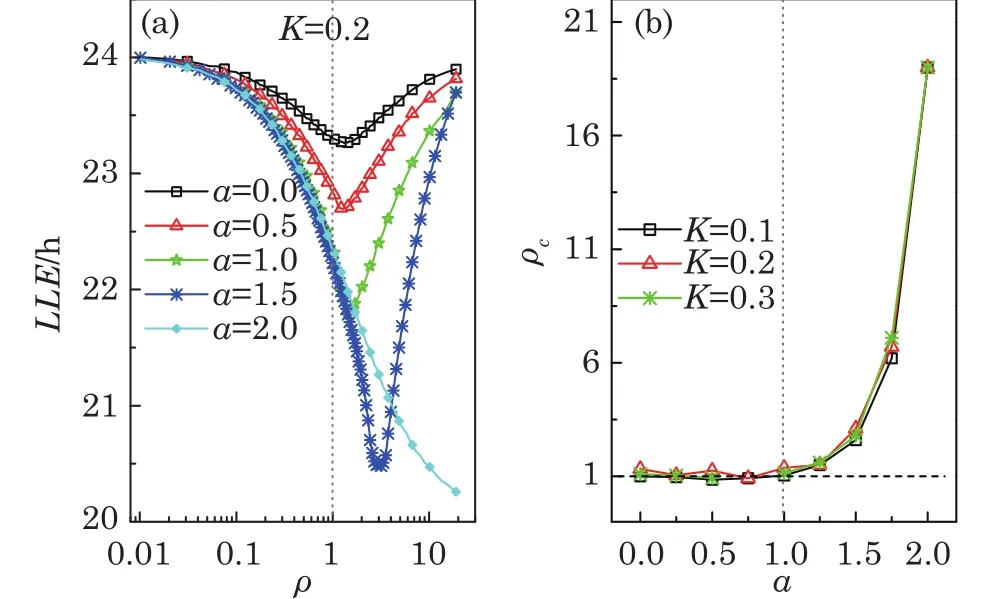
The parameters ciand Lirely on the location of the neurons.If the neuron i is situated in the VL region(i≤ pN),the parameters are ci=a and Li=Kfsin(Ωt),where the parameter p represents the ratio of the number of neurons sensitive to the light information;and if the neuron i is located in the DM region(pN The details for the numerical simulations are presented as follows.Without special statement,the values of parameters are set as γ =1,τ=24,p=0.5,K=0.2,N=2,and C=1 throughout the present article.[4]We use the fourth-order Runge-Kutta method with time increments of 0.01 h.The initial 2,000,000 time steps(2,000 h)were neglected in order to avoid the in fluence of transients.If the mean square deviation(MSE)between the periods of the SCN neurons and the period of the external cycle is less than 0.000,01 h,the SCN is assumed to be entrained to the external cycle. Figure 1 shows illustrative examples for the effect of the ratio ρ on the entrainment of the SCN to a 21 h external cycle with ρ =0.33(a), ρ =1.0(b),and ρ =9.0(c),when the intrinsic amplitude of the VL neurons is a=2.0.Because the phase differences of the VL neurons to the external cycle or/and the DM neurons to the external cycle are fluctuated over time,both the VL and the DM are not entrained to the external cycle,when the ratio is ρ=0.33 in(a)or when the ratio is ρ=1 in(b).When the ratio increases to ρ=9.0,the phase differences are altered to be stable in that both the VL and the DM are entrained to the external cycle(c).Therefore,the ratio ρ affects in the entrainment ability of the SCN to the external cycle. Next,the quantitative relationship of the entrainment range to the ratio ρ is examined for five typical intrinsic amplitudes a of the VL in Fig.2.In(a),the relationship is parabolic-like for the cases of a<2.0,and the relationship is monotonically decreasing for a=2.0.Nevertheless,there are difference in the positions of troughs(or the positions of the smallest value for the LLE)ρcamong these cases of a.In particular,ρcis around 1 in the cases of a ≤ 1.0,whereas ρcis around 3 and around 19 when the amplitude is a=1.5 and a=2.0,respectively.Hence,the value of ρcdepends on the intrinsic amplitude a.Consequently,we examine the relationship of ρcto a,where three values of the strength K are taken into account.It is visible that,for each K,the ρcis around a constant of 1 if the intrinsic amplitude is a≤1.0,and interestingly,the ρcincreases with the increase of a when the intrinsic amplitude is larger than 1(a>1.0).Therefore,ρ affects the entrainment range of the SCN,the largest entrainment range(the smallest LLE)is obtained when the ratio is ρ = ρcfor each case of a,where ρcdepends on the value of a. Fig.1 Exposed to a 21 h light-dark cycle,the distinct temporal evolutions of the SCN neurons with typical ratios r.The ratio is ρ=0.33,i.e.,Kf=0.05 and g=0.15(a),ρ =1.0,i.e.,Kf=0.1 and g=0.1(b),and ρ =9.0,i.e.,Kf=0.18 and g=0.02(c).The intrinsic amplitude of the VL and the DM are selected as a=2 and b=0 respectively.The gray(white)area corresponds to the darkness(light). Fig.2 The dependence of the LLE on the ratio ρ and the intrinsic amplitude a of the VL.The relationship of the LLE to the ratio ρ for typical amplitudes a in(a),and the relationship of rcto a in(b). Moreover,the quantitative relationship of the LLE to the ratio ρ is examined with p=0.5 and p=0.25,respectively,when the total number of SCN neurons is N=100 in Fig.2.We observe that the results are consistent with Fig.2 in both(a)and(b),in other words,the ratio ρ affects the entrainment range and the position of trough for the LLE(ρc)depends on the value of a.We also examine the case of nonidentical intrinsic periods of the neurons(Fig.4).The results are consistent with those shown in Fig.3.The parameters for Fig.4 are the same as Fig.3,except that a new parameter ηiis introduced. ηiis multiplied to τiin Eq.(1),which satisfies a normal distribution with a mean of 1 and a standard deviation ϵ. ϵ represents the degree of heterogeneity in the intrinsic neuronal period,whose value is selected as 0.02.If ϵ is 0,Fig.4 is reduced to Fig.3. Fig.3 The relationship of the LLE to the ratio ρ for five typical intrinsic amplitudes a of the VL neurons,when the ratio of light-sensitive neurons is p=0.50(a)and p=0.25(b).The total number of SCN neuronal oscillator and the strength is N=100 and K=0.2,respectively.This figure corresponds to Fig.2(a). Fig.4 The relationship of the LLE to the ratio ρ,when the intrinsic periods of the neurons are nonidentical.The ratio of light-sensitive neurons is p=0.50(a)and p=0.25(b).The value of parameters are the same as in Fig.3,except that the standard deviation ϵ is set as 0.02. In this section,we will present analytical results to explain the parabolic-like relationship between the LLE and ρ,and why ρcis close to 1 when the amplitude is a ≤ 1,and why ρcincreases with the increase of a if a>1.For simplicity,a model composed of two oscillators,i.e.,the VL and the DM,is presented as follows: where the VL and the DM is denoted by v and d,respectively,and the mean field F is the term(xv+xd)/2.For convenience,we transform Eq.(3)from Cartesian Coordinates to Polar Coordinates,and obtain xv=rvcosθv,yv=rvsinθv,xd=rdcosθd,yd=rdcosθd.Substituting them into Eq.(3),we obtain If all the oscillators are entrained to the external cycle,we obtain.Let the phases be θv= Ωt+ϕvand θd= Ωt+ϕd.Considering the averaging method developed by Krylov and Bogoliubov as used in Refs.[4,22,25],ϕ has a lower time scale than Ωt.Letting the phase difference bewe obtain The entrained frequencies Ω of the two oscillators are affected by the following terms besides the intrinsic frequencies.For the VL oscillator,the frequency Ω is affected by the light term L= −Kfcosϕv/2rvand the coupling term E1=(rd/4rv)g sinα;for the second oscillator,the frequency Ω is only affected by the coupling term E2= −(rv/4rd)g sinα.In order to obtain the lower limit of entrainment(LLE),i.e.,Ω reaches its largest value,both the light term L1and the coupling term E1should be the largest(cosϕvis close to−1 and sinα is close to 1),and the coupling term E2should also be the largest(sinα is close to−1),respectively.However,the signs of E1and E2are different,so E1and E2can not reach their largest values simultaneously and there is a balance between sinα and cosϕvfor the LLE.We will find the balance for the typical conditions of a≫b,a≈b,and a≪b. Additionally,there is a constraint relationship between sinα and cosϕv.From the second equation and last equation of Eq.(6),the relationship between sinα and cosϕvis found as When the intrinsic amplitude a is much larger than b,e.g.a=2 and b=0,the amplitude rvis also much larger than rd(see Fig.1),and g and Kfare small terms compared to a.Becauseis a small term,independent of the value of cosϕv,the condition−1≤ sinα≤ 1 can satisfy in Eq.(7).Hence,cosϕvcan be equal to −1 in order to obtain the LLE,and Eq.(7)is reduced to Submitting Eq.(8)to Eq.(6),we obtain where rv=a+g/4γ≈a is obtained from the third equation of Eq.(6).Therefore,we prove that there is a positive correlation between the LLE(ΩLLE)and ρ when a is much larger than b(e.g.a=2 and b=0)in Fig.2(a).Additionally,because the relationship is positive,ρccan be very large,e.g.ρc=19 in Figs.2(a)and 2(b). When the intrinsic amplitude a is close to b,e.g.a=1 and b=1,the amplitude rvis also close to rd,and Kfand g are small values compared to rvand rd.Hence,Eq.(7)is reduced to where the values of sinα and cosϕvdepend on ρ. If ρ is smaller than 1,cosϕ is−1 and sinα is−ρ in order to obtain the LLE.From the last equation of Eq.(6),we obtain ΩLLE= ω+ρg/4≈ ω+Kf/4≈ ρ.Therefore,we prove that the LLE(ΩLLE)increases with the increase of ρ if the ratio ρ is smaller than 1 with a ≈ b in Fig.2(a). If ρ is close to 1,both sinα and cosϕ are equal to −1 in order to obtain the LLEc.From the last equation of Eq.(6),we obtain ΩLLEc= ω +g/4. If ρ is larger than 1,sinα is−1 and cosϕ is−1/ρ in order to obtain the LLE.From the last equation of Eq.(6),we obtain ΩLLE= ω +g/4 ≈ 1/ρ.Therefore,we prove that the LLE decreases with the increase of ρ if the ratio ρ is larger than 1 with a≈ b in Fig.2(a). Taking these three cases of ρ into account,we have proved that the parabolic relationship between the LLE and ρ,and the LLEcis obtained with ρc≈ 1,when a is much smaller than b. When the intrinsic amplitude a is much smaller than b,e.g.a=0 and b=2,the amplitude rvis much smaller than rd,and g and Kfare small terms compared to rd.Hence,Eq.(7)is reduced to where the values of sinα and cosϕvdepend on ρ. If the ratio ρ is much smaller than 1,i.e.,g ≫ Kf,in order to obtain the LLE,Eq.(11)is altered to be cosϕv= −1,sinα = −ρ.From the third equation and first equation of Eq.(6),we obtain rd=b+g/4γ andrespectively.Hence,from√ the last equation of Eq.(6),we obtainρg=Kf∝ ρ.Therefore,we have proved that the LLE(ΩLLE)increases with the increase of ρ if the ratio ρ is much smaller than 1 with a≪b in Fig.2(a). If the ratio ρ is much larger than 1,i.e.,g ≪ Kf,in order to obtain the LLE,Eq.(11)is altered to be sinα = −1,cosϕv= −1/ρ.From the third equation and first equation of Eq.(6),we obtain rd=b+g/4γ ≈ b andrespectively.Hence,from the last equation of Eq.(6),we obtainTherefore,we prove that the LLE(ΩLLE)decreases with the increase of ρ if the ratio ρ is much than 1 with a ≪ b in Fig.2(a). If the ratio ρ is close to 1,i.e.,g ≈ Kf,in order to obtain the LLEc,Eq.(11)is altered to be sinα =cosϕv=−1.From the third equation and first equation of Eq.(6),we obtain rd=b+g/4γ ≈ b and rv=g/4γ,respectively.Hence,from the last equation of Eq.(6),we obtainΩLLEc=ω+grv/4rd= ω+g2/16γb. Taking these three cases of ρ into account,we have proved that there is a parabolic relationship between the LLE and ρ,and the maximal LLE is obtained with ρc≈ 1,when a is close to b. The entrainment range differs among various species.[3−5]Previous studies aimed to find answers for the diversity and found that the entrainment range is affected by the sensitivity to the light information and coupling strength of the SCN neurons,respectively.However,the effect of the interplay between these two key factors is yet unknown.In the present study,we examined whether the entrainment range is affected by the ratio between the sensitive strength and the coupling strength.We found that there is a parabolic-like relationship between the entrainment range and the largest entrainment range is obtained with a suitable ratio.Interestingly,the value of this suitable ratio depends on the comparison in the intrinsic amplitudes between the VL neurons and the DM neurons.If the former amplitudes are not larger than the latter,this value is a constant around 1;whereas if the former are larger than the latter,this value increases with the increase of the VL amplitudes. In the experiments,it has been observed that both the cellular coupling strength and sensitive strength are attenuated in the aging mice.[26−27]These attenuations lead to the decrease of the entrainment range of the mice.It is interesting to examine whether the ratio of these two strengths is altered during aging in future experiment.Our finding will shed light on the effects of the interplay between the sensitive strength and the coupling strength,as well as the understanding for the diversity of the entrainment range among species.3 The Effects of Ratio on the Entrainment Range



4 Analytical Results
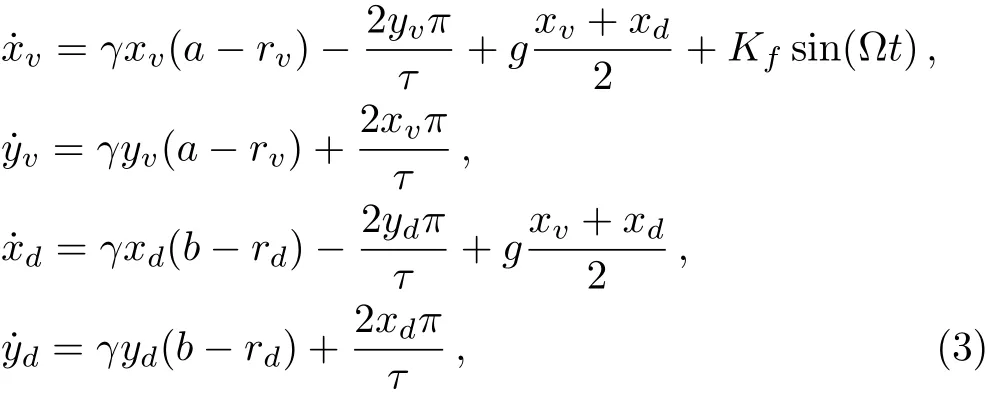


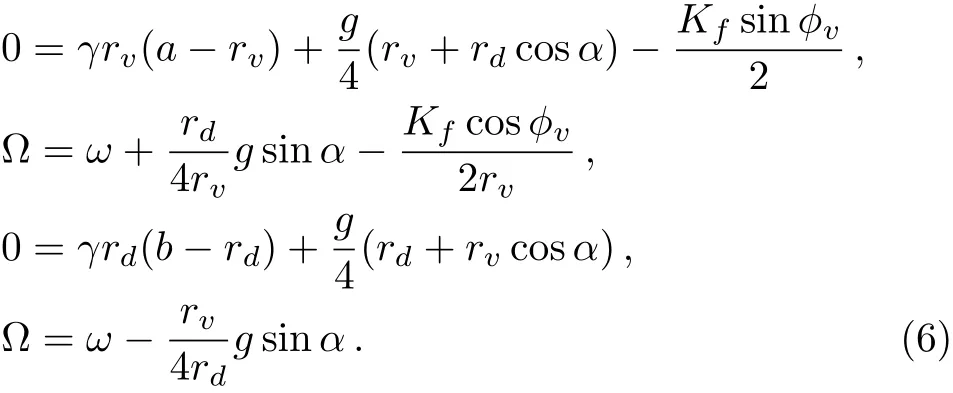
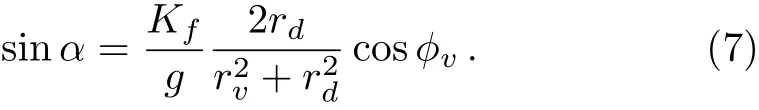
4.1 a is much larger than b
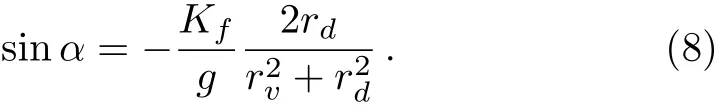

4.2 a is close to b
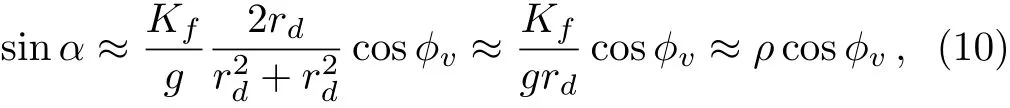
4.3 a is much smaller than b
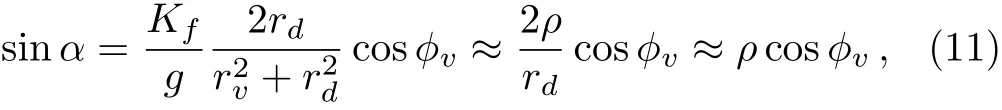
5 Conclusion and Discussion
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
- Communications in Theoretical Physics的其它文章
- Mixed Local-Nonlocal Vector Schrödinger Equations and Their Breather Solutions∗
- Circular Semi-Quantum Secret Sharing Using Single Particles∗
- Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation∗
- Runaway Directions in O’Raifeartaigh Models∗
- The 1/NcExpansion in Hadron Effective Field Theory∗
- Quasinormal Modes of the Planar Black Holes of a Particular Lovelock Theory∗
