The 1/NcExpansion in Hadron Effective Field Theory∗
Guo-Ying Chen(陈国英)
Department of Physics and Astronomy,Hubei University of Education,Wuhan 430205,China
Abstract We study the Ncscalings of pion-nucleon and nucleon-nucleon scatterings in hadron effective field theory.By assuming Witten’s counting rules are applied to matrix elements or scattering amplitudes,which use the relativistic normalization for the nucleons,we find that the nucleon axial coupling gAis of order N0c,and a consistent large Nc counting can be established for the pion-nucleon and nucleon-nucleon scatterings.We also justify the nonperturbative treatment of the low energy nucleon-nucleon interaction with the large Ncanalysis and find that the deuteron binding energy is of order 1/Nc.
Key words:large NcQCD,effective field theory,nucleon-nucleon interaction
In the seminal paper Ref.[1],’t Hooft showed that QCD has a hidden expansion parameter 1/Nc.With the 1/Ncexpansion the QCD coupling constant g is of order 1/,and gluons are denoted by double lines.By counting the number of interaction vertexes and closed color loops,one can figure out the Ncorder of a specific Feynman diagram.It is then found that in the large Nclimit,the leading contribution comes from planar diagrams with minimal quark loops.The idea to expand QCD in 1/Ncis very attractive,as it explains hadron phenomenology successfully,for instance the OZI suppression rule.The extension of the 1/Ncexpansion to baryons was first carried out by Witten.[2]The 1/Ncexpansion of baryons,which are bound states of Ncvalence quarks and have masses of order Nc,is more complicated than that of mesons.Using quarks and gluons as degrees of freedom,Witten showed that meson-baryon coupling is of order,meson-baryon scattering amplitude is of order,and baryon-baryon scattering amplitude is of order Nc(these results are called the large Nccounting rules of Witten in this manuscript).It is interesting to study whether a realistic hadron effective field theory using baryons and mesons as degrees of freedom can reproduce the large Nccounting rules of Witten.We will see in the following that this is not a clearly solved problem.
First of all,we consider the pion-nucleon scattering.The leading pion-nucleon scattering diagrams in chiral expansion are shown in Fig.1.In chiral theory,the pionnucleon vertex is proportional to the factor gA/fπ,where fπis the pion decay constant with order,and gAis the nucleon axial coupling constant,which is assumed to be of order Ncin both the nonrelativistic quark model.[3]and the skyrme model.[4]The nucleon propagator is of order.[5]Therefore,both amplitudes of Figs.1(a)and 1(b)are proportional to the factor(gA/fπ)2and are of order Nc,and Fig.1(c)is proportional to 1/and of order 1/Nc.Clearly these results contradict the large Nccounting rules of Witten.A solution to this puzzle has been proposed in Refs.[6–8],and we give a short review here for the convenience of further discussions.The axial vector current matrix element in the nucleon is of order Ncand can be written as[8]

where the Ncdependence has been explicitly factored out,so 〈N|Xia|N〉and g are of order one.The sum of the scattering amplitudes for the pole diagrams of πa(q)+N(P)→ πb(q′)+N(P′)reads
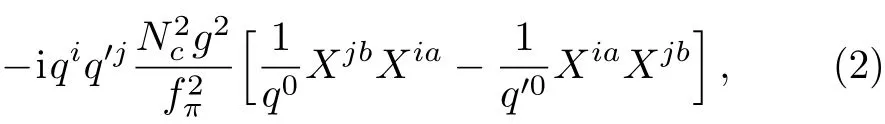
where the amplitude is written in the form of an operator acting on nucleon states,and q0=q′0as both initial and final nucleons are on-shell.One can see explicitly that the above amplitude is of order Ncand violates the unitarity.The solution to this puzzle is the commutation relation in the large Nclimit

which is usually called the large Ncconsistency condition.The solution of the large Ncconsistency condition requires to consider all the possible baryon states degenerate with the nucleon in the intermediate states of the scattering.For instance,besides the nucleon,∆should also be included as an intermediate state in the pion-nucleon scattering,and the coupling gπN∆can be determined in terms of gπNNusing the large Ncconsistency condition.The large Ncconsistency condition can be derived from the spin- flavor algebra.Consider the two- flavor case,the SU(4)generators Ji,Ia,and Giasatisfy the spin- flavor algebra

Rescaling the generator Giaby a factor of 1/Ncand taking the large Nclimit,

we can find that the commutation relation for[Gia,Gjb]turns into Eq.(3)in the large Nclimit,as the order of baryon matrix elements of J and I are at most of Nc.A careful study found that the commutator[Xia,Xjb]is of order 1/,[9]hence Eq.(2)is of order 1/Nc,which is the same as the amplitude of Fig.1(c).Since Witten’s counting rules suggest that the leading contribution should come from orderdiagrams in the 1/Ncexpansion,one may wonder why the pion-nucleon scattering amplitude is dominated by order 1/Ncdiagrams instead of orderdiagrams.
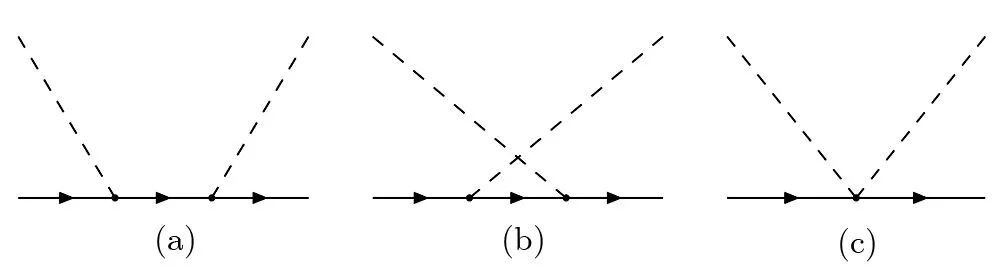
Fig.1 Pion-nucleon scattering diagrams in leading chiral expansion.
Secondly,there is difficulty in matching the Nccounting of the nucleon-nucleon potential calculated at the quark-gluon level to that calculated at the hadronic level.The dominant nucleon-nucleon interaction is generically of order Ncwith the analysis at the quark-gluon level.[2]This can be understood from the one-gluon exchange diagrams in Fig.2,where each gluon coupling has a factor 1/,and there areways to choose a pair of quarks.In studying the Nccounting of the nucleon-nucleon potential,Refs.[10–11]consider the kinematic region pfor the nucleon and assume that quark-line connected diagrams such as Fig.2 are of order Ncleads to a potential of order Nc.It should be note that the kinematic region is different from that was considered in Witten’s paper,where p∼Nc.[2]The reason is that,if p∼Nc,which is the same order as the nucleon mass,the nucleon is a relativistic particle,and this kinematic region is beyond the scope of the low energy hadron effective field theory.[12]At the hadronic level,it seems straightforward to see that the one-meson exchange potential is of order Nc,for example the one-pion exchange potential is proportional to the factor(gA/fπ)2and of order Nc.At the two-meson exchange level,diagrams(for instance,the crossed-box diagram)with four nucleon-meson vertexes are of orderand will contribute to the potential,but Ref.[12]shows that there is a cancelation of the retardation effect of the box graph against the contribution of the crossed-box diagram,therefore the dominant nucleon-nucleon potential remains to be of order Nc.Nevertheless,it is difficult to show that whether such cancelations will happen in all multi-meson exchange levels.Actually,it is found that at the three-and higher-meson exchange level the potential derived from the hadronic theory can be larger than that of the quark-gluon theory.[13]This problem is called the large Ncnuclear potential puzzle.
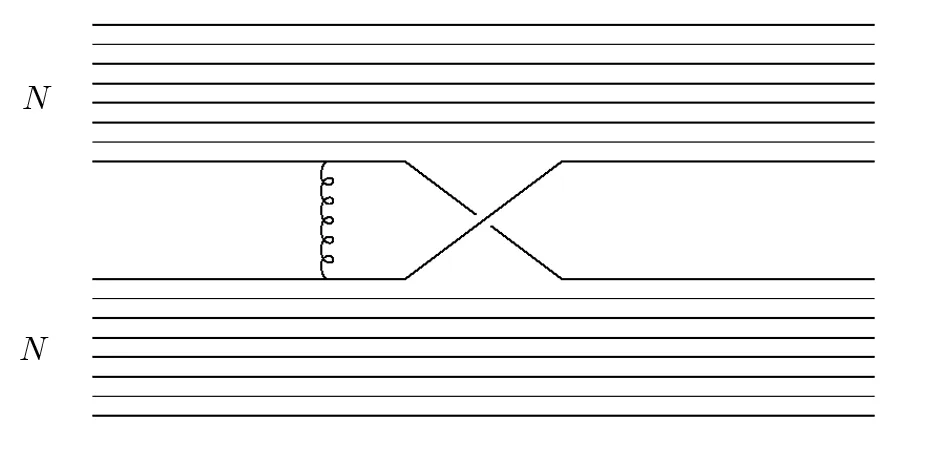
Fig.2 A typical diagram of order Nc,which contributes to the nucleon-nucleon interaction in large NcQCD.
Two possible resolutions to the large Ncnuclear potential puzzle are suggested in Ref.[13].One possibility is that necessary cancelations might happen if the hadroniclevel calculation is reorganized in some other way.A tentative study on this direction is done in Ref.[14],where the hadronic-level calculation is reorganized in the way that the potential is energy-independent.The other possibility is that the Ncscaling rule of the nucleon-nucleon potential proposed in Refs.[10–11]may be invalid.This can be plausible by noting that some nuclear phenomena may be difficult to understand if the nucleon potential is of order Nc,for example,the deuteron binding energy is a small number in reality,i.e.,B=2.2 MeV.Although it is generally believed that such small binding energy results from delicate cancellation,which occurs at Nc=3,[15−16]it will still be interesting to find an alternative solution,which does not rely on the fact that Nc=3 in the real world.In addition,since the nucleon kinetic energy is order,if the potential is order Ncnucleon matter forms a crystal in the large Nclimit.However,nuclear matter appears to be in liquid state rather than in crystal state in reality.Generally,nuclear phenomena seem to prefer a small potential value,and this observation motivates Refs.[17–18]to proposed a re fined quark model,which gives gA∼Nc0,thus the one-pion exchange potential is of order
From the above discussions,we can see that it is not clear how to reproduce the large Nccounting rules of Witten consistently in a realistic hadron effective field theory.In this paper we try to propose a simple way to resolve the above difficulties.We find that we can have a consistent large Nccounting in hadron effective field theory if we assume Witten’s counting rules are applied to matrix elements or scattering amplitudes,which use the relativistic normalization for the nucleons.Our work is organized as following:we first discuss the difference of Ncscalings between the relativistic and nonrelativistic normalizations.With the relativistic normalization,we then discuss the Ncscalings of pion-nucleon and nucleon-nucleon scatterings.We finally extend our study to the meson-meson scatterings and find that loosely-bound meson-meson molecular states may not exist in the large Nclimit.
The leading non-relativistic chiral Lagrangian for the pion-nucleon coupling reads
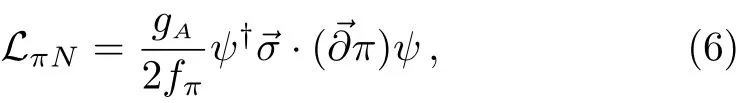
where ψ is the nucleon doublet and π = τiπi.If gAis of order Nc,the pion-nucleon coupling is proportional to gA/fπif gAas suggested in Refs.[17–18],the pion-nucleon coupling is of order,which seems to contradict the large Nccounting rules of Witten.One should note that in the above Nccounting Feynman rules for the external nucleon lines are assumed to be independent of Nc,or explicitly one use the nonrelativistic normalization for the nucleon and of order,which is just the result of Witten.But

However from the Dirac theory,we know that the Feynman rule for the external nucleon line is us(p),which reduces to(χsis the two-component spinor)in the nonrelativistic limit and obviously depends on Nc.Thus the relativistic normalization for the nucleon reads

where we have taken the nonrelativistic limit for the Dirac spinor us(p)to simplify the Nccounting in the low energy effective field theory.Scattering amplitudes,which use Eq.(8)as the normalization condition can be understood as the nonrelativistic reduction of the relativistic form.In this work,we will use the relativistic normalization for the scattering amplitudes,thus the relation between our defined scattering amplitude M(p1,p2→pf)and the S-matrix reads

where
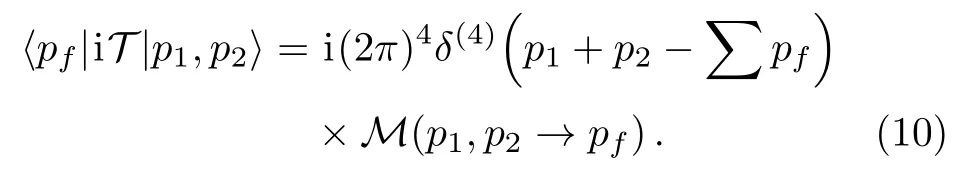
To obtain the scattering amplitudes with the nonrelativistic normalization MNR,one takes the limit→0 and drops factors of,which come from external nucleon spinor function us(p).For example,for the nonrelativistic nucleon-nucleon elastic scattering,we can have MNR=M/(2mN)2.One should note that we only discuss the nonrelativistic scattering in this work as the relativistic normalization reduce to the form in Eq.(8).We will find that Witten’s large Nccounting rules can be consistent,if one assumes that these rules are applied to matrix elements or scattering amplitudes,which use the relativistic normalization for the nucleon.
We now return back to the discussion of the pionnucleon coupling.With the normalization in Eq.(8),there is a factor offor each external nucleon line,and the pion-nucleon coupling is proportional to mN(gA/fπ).Our matching scheme is that we assume Witten’s counting rules are applied to matrix elements or scattering amplitudes,which use the relativistic normalization for the nucleon,we then find that gA∼as the pion-nucleon coupling is orderfrom Witten’s rules.Thus we have shown that if gAas suggested in Refs.[17–18],the Nccounting of the pion-nucleon coupling can be consistent with Witten’s result.In the following we will count gAas order,since it is the consequence of our assumption.
Now we come to discuss the Ncscaling of the pionnucleon scattering.The scattering amplitude for the pionnucleon scattering given in Eq.(2)is written with the nonrelativistic normalization.But noting that,while factors of,which come from the external nucleon lines are dropped in Eq.(2),such factor is kept for the baryon propagator.This can be obviously since the baryon propagator i/q0in Eq.(2)is obtained from the Dirac propagator by taking the nonrelativistic limit

where mBis the mass of intermediate baryon,vµis the four-velocity of the initial nucleon,i.e.,Pµ=mNvµ,and it is taken to bein the nonrelativistic limit.With the relativistic normalization,factors ofshould be restored for external nucleon lines in the scattering amplitudes,then the scattering amplitudes for Figs.1(a)and 1(b)are proportional to mN(gA/fπ)2,and the amplitude for Fig.1(c)is proportional to mN/,all of which are of orderand consistent with the large Nccounting rules of Witten.Actually what we have illustrated in the above is that if the assumption that Witten’s rules are applied to matrix elements or scattering amplitudes,which use the relativist normalization for the nucleon is adopted for the pion-nucleon coupling,the Ncscaling of the pion-nucleon scattering will be consistent with this assumption.
To have a consistent Nccounting with the nonrelativistic normalization,one can redefine the nucleon field by dividing a factor of,then factors ofare not needed in the Feynman rules for the external nucleon lines.Meanwhile,the nucleon propagator should be i/2mNq0instead of i/q0as the new defined nucleon field has the dimension one,and gAshould absorb a factor of 2MN,which is dimension one and of order Nc.With this convention the scattering amplitudes for Figs.1(a)and 1(b)are proportional to(gA/fπ)2(1/2mNq0),which is also of orderas gAis of the order Nc.Therefore,we can see that physical results do not depend on the normalization conventions as long as they are used consistently.The advantage of using the relativistic normalization is that gAis a dimensionless constant as usually defined in the text book.
It is worth to mention that,although with the relativistic normalization gAis of order,the commutation relation in Eq.(3)still holds in the large Nclimit.This can be shown by rewriting the axial current matrix element in Eq.(1)with the normalization in Eq.(8)

where〈N|Xia|N〉and g are of order one,and the product g〈N|Xia|N〉is different from that in Eq.(1)by an Ncindependent factor 2mN/Nc.Since the matrix element of Xiadefined in Eq.(12)is different from that in Eq.(1)by an Ncindependent factor,operators Xiadefined in Eq.(12)still satisfy the commutation relation in Eq.(3),i.e.,the large Ncconsistency condition.The commutation relation Eq.(3)arises because the axial vector current matrix element grows with Nc.With our normalization,gAis of order,but the axial vector current matrix element is still of order Nc,thus the commutation relation Eq.(3)still holds.Taking this contracted spin- flavor symmetry into account,we should also include∆particle in the intermediate state,then the contributions from pole diagrams Figs.1(a)and 1(b)vanish in the large Nclimit.
We then come to the nucleon-nucleon scatterings.As in the above,we assume Witten’s counting rules are applied to the nucleon-nucleon scattering amplitudes,which use the relativistic normalization.In this way,nucleonnucleon scattering amplitudes with the relativistic normalization are of order Nc.The order Ncscattering amplitude leads to a potential of order,as factors of be dropped in the scattering amplitude to obtain the nonrelativistic potential.Therefore our resolution to the nuclear potential puzzle corresponds to the second possibility suggested in Ref.[13],i.e.,the assumption that the dominant nucleon-nucleon potential is of order Ncis somewhat heuristic and may be invalid.We will take the pionexchange as an example to show explicitly how the large Ncnuclear potential puzzle can be resolved.The nucleonnucleon scattering amplitude for the one-pion exchange diagram is proportional to the factor(mN(gA/fπ))2,which is of order Ncand again consistent with our assumption.The amplitude of two-pion exchange crossed-box diagram is proportional to,which is of orderand thus is suppressed by 1/Nc.It is obvious that more-pion exchange diagrams,which are two-nucleon inreducible,will be suppressed by more powers of 1/Nc.Thus one can see that the nucleon-nucleon potential is at most of,which come from the external nucleon lines should orderand this large Nccounting rule will not be violated at the multi-pion exchange level.It is straightforward to see that similar conclusion can be obtained for other meson-exchange diagrams,in particularly the sigmaexchange potential is also of order
So far,we have shown that a consistent large Nccounting in hadron effective field theory can be established,if we assume Witten’s counting rules are applied to matrix elements or scattering amplitudes,which use the relativistic normalization for the nucleons.Nevertheless there are still two points in nucleon-nucleon scatterings need to be further investigated.The first point is that one may wonder whether the order Ncscattering amplitude violates the unitarity.We now show that this does not happen in the nucleon-nucleon scattering.To be specific,let us consider the single channel S-wave nucleon-nucleon scattering.The S-matrix for the S-wave nucleon-nucleon scattering can be written as S=1+i(p/8πmN)M,where p is the nucleon momentum and M is the scattering amplitude,which use the relativistic normalization.Unitary condition,i.e.SS†=1,requires that
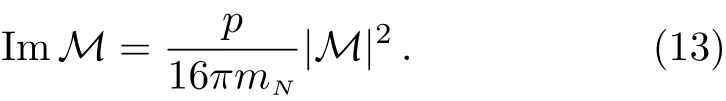
We consider the kinematic region p∼as in Ref.[11]and denote the Ncscaling of the amplitude as ReM∼,Im,M∼.The unitary condition in the large Nclimit can then be written as
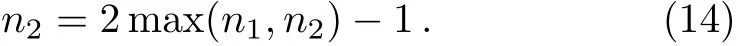
The solution to the above condition reads

Thus one can see that the unitary condition can be satisfied if the scattering amplitude is of order Nc.
The second point is that in hadron effective field theory deuteron corresponds to a bound state pole,which emerges from the non-perturbative summation of the nucleon-nucleon scattering amplitudes,hence it is interesting to investigate whether such non-perturbative summation is justified in the large Nclimit.Following,we will study this point in detail with a low energy pionless effective field theory.
Let us now consider the low energy pionless effective field theory in the3S1channel.[19−21]The leading order operator in the chiral expansion for nucleon-nucleon interactions reads
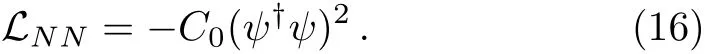
Feynman diagrams generated by this interaction vertex are shown in Fig.3.We can identify the order Ncquarkconnected diagrams,such as Fig.2,as the tree diagram in Fig.3,and identify the quark-disconnected diagrams,such as Fig.4,as the one-loop diagram in Fig.3.The amplitude for the tree diagram in Fig.3 reads
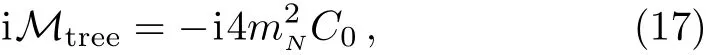
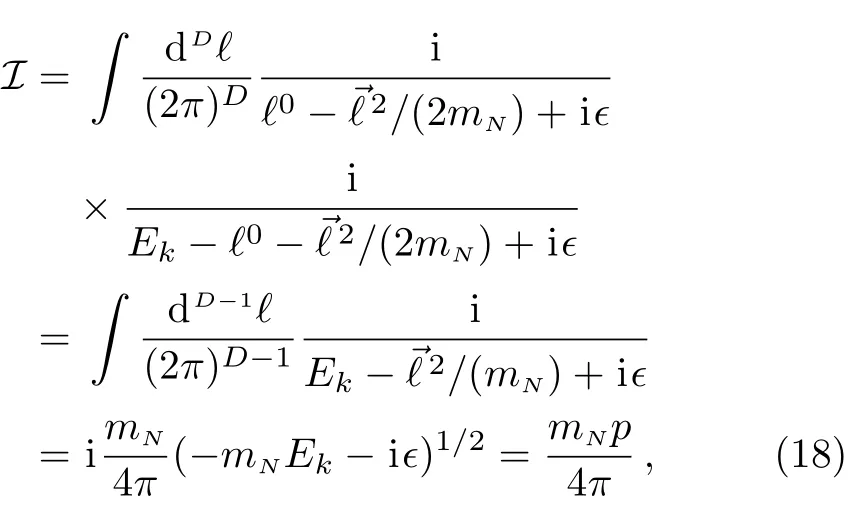
where Ek=is the total kinetic energy of the twonucleon in the center of mass frame.In the chiral expansion the three-momentum of the nucleon is treated as small scale and has the same order as mπ,thus we assume p to be independent of Ncas in Ref.[11].It is worth mentioning that the nucleon propagator used here is order Ncand different from that in Eq.(2),as the termshould also be included in the propagator to avoid the infrared divergence in the two-nucleon reducible diagrams.[19]With the result for loop integral,one can obtain the one-loop amplitude
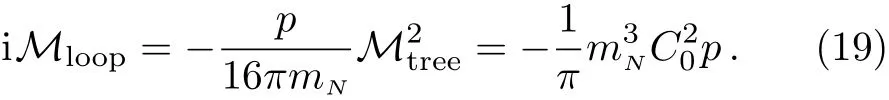
We can find that the one-loop amplitude is of order Nc,which is the same as that of the tree diagram.This result is somewhat surprising at the first sight,as quarkdisconnected diagram Fig.4 seems to be of order.Actually to count the Ncorder of Fig.4 one should note that such a diagram contains nucleon propagators and loop,thus its Ncorder can be the same as that obtained in the hadron effective field theory,i.e.,O(Nc).It is straightforward to count the Ncorder of all the other diagrams in Fig.3.One can find that all the diagrams in Fig.3 are of order Nc,hence the amplitude at the leading order in the 1/Ncexpansion should come from the non-perturbative summation of all the diagrams in Fig.3.The re-summed amplitude reads
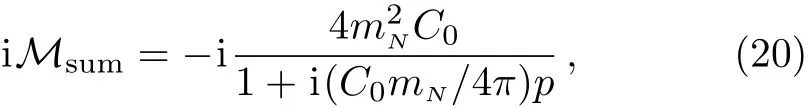
which is obviously of order Nc.The partial wave S-matrix can then be written as
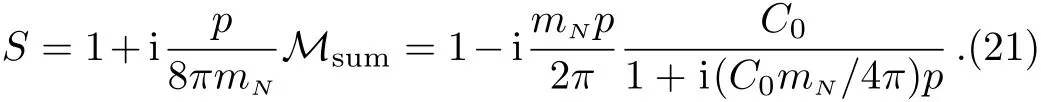
One can find that,although Msumis of order Nc,the S-matrix is independent of Ncand satisfies the unitary condition,i.e.SS†=1.Actually it has already been shown in Ref.[20]that all the diagrams in Fig.3 need to be summed,because they all are at the leading chiral order O(p−1).Here we have shown that this summation is also justified in the large Ncexpansion.The deuteron corresponds to a bound state pole at Ek=−B in Eq.(20),where B is the binding energy,

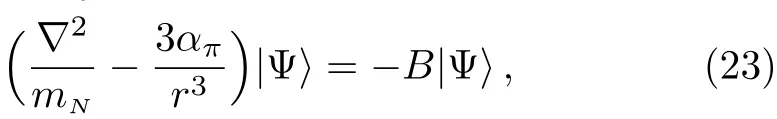
where

Because the three-momentum of the nucleon and gAare of order,both kinetic energy and tensor potential energy in the left hand side of Eq.(23)are of order,and the binding energy B is of order,which is the same as that in the pionless effective field theory.This conclusion remains unchanged even if an additional termis included in the potential.In contrast,by treating gAas O(Nc),Ref.[22]assumes that the coordinate scales as,or equivalently the three-momentum carried by the nucleon scales as,then B scales as.However,as mentioned in Ref.[22],if the three-momentum carried by the nucleon scales as,the effective field theory will be constrained to threshold.

Fig.3 Feynman diagrams generated by the contact interaction.
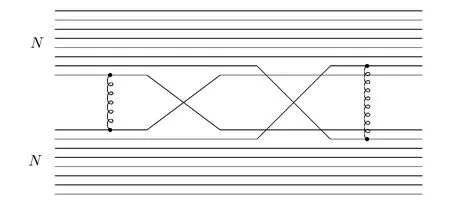
Fig.4 A typical quark-disconnected diagram.
It is interesting to extend the above analysis to discuss the existence of S-wave meson-meson molecular states.We will find that the Ncanalysis of the deuteron cannot be straightforwardly extended to the meson-meson case as the meson-meson scattering amplitudes and meson masses have different Nccountings.In effective field theory approach,an S-wave meson-meson molecular state corresponds to a bound state pole in the elastic meson-meson scattering amplitude coming from the summation of all the diagrams in Fig.3.[23]Similar to Eq.(22),the binding energy B for the meson-meson molecular state reads

In summary,we have tried to propose a possible solution to overcome the difficulties,which are encountered in reproducing the large Nccounting rules of Witten in hadron effective field theory.We find that a consistent large Nccounting can be established if we assume Witten’s counting rules are applied to matrix elements or scattering amplitudes,which use the relativistic normalization for the nucleons.We also find that at the leading order in the 1/Ncexpansion,the S-wave nucleon-nucleon scattering should be treated nonperturbatively,and the deuteron binding energy is of order 1/Nc,which is consistent with the nuclear phenomena.In contrast,the S-wave meson-meson interaction is weak,and loosely-bound meson-meson molecular states may not exist in the large Nclimit.
Acknowledgments
I would like to thank Yu Jia for helpful discussions and J.Ruiz de Elvira for valuable comments.Part of this work was done during my visit to Institute of Theoretical Physics,Chinese Academy of Science in Beijing.
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
- Communications in Theoretical Physics的其它文章
- Electron Transport Properties of Graphene-Based Quantum Wires∗
- Magnetic Properties of XXZ Heisenberg Antiferromagnetic and Ferrimagnetic Nanotubes∗
- On the Singular Effects in the Relativistic Landau Levels in Graphene with a Disclination∗
- Super-sensitivity in Dynamics of Ising Model with Transverse Field:From Perspective of Franck-Condon Principle∗
- New Feedback Control Model in the Lattice Hydrodynamic Model Considering the Historic Optimal Velocity Di ff erence Effect∗
- A Class of Rumor Spreading Models with Population Dynamics∗
