Super-sensitivity in Dynamics of Ising Model with Transverse Field:From Perspective of Franck-Condon Principle∗
Lei Xu(徐磊)and Li-Ping Yang(杨立平),2,†
1Beijing Computational Science Research Center,Beijing 100084,China
2Birck Nanotechnology Center and Purdue Quantum Center,School of Electrical and Computer Engineering,Purdue University,West Lafayette,Indiana 47906,USA
AbstractWe study the role of Franck-Condon(F-C)principle in the dynamics of a central spin system,which is coupled to an Ising chain in transverse field.The transition process of energy levels caused by the excited central spin is studied to manifest the quantum critical effect through the Franck-Condon principle.The super-sensitivity of this quantum critical system is demonstrated clearly from the properties of Franck-Condon factors.We analytically show how spin numbers,coupling strength and order parameter of the Ising chain sensitively effect on the energy level populations in dynamical evolution near the critical point.This super-sensitivity and criticality are explicitly displayed in absorption spectrum.
Key words:Franck-Condon principle,Ising model,quantum phase transition,super-sensitivity
1 Introduction
The Franck-Condon(F-C)principle is originally put forward in molecular physics by Franck to analyze the mechanism of photon-induced chemical reactions.[1]Condon later introduced this principle and expanded it in the semi-classical general formulation.[2]The early investigations about F-C principle mostly focused on electronphonon coupling systems.[3−7]Lax then applied this to solid-state system to calculate the emission and absorption spectrum.[8]The principle concerns about the probability intensity of the vibration-assisted electron transition spectrum in an electron-phonon coupling system.The transition of system from one vibrational level to another will be companied with a change of vibrational configuration and the transition will be more likely to happen if the two vibrational wave functions overlap more significantly.This overlap(usually called as F-C factor)is proportional to the transition probability and the so-called “vertical” transition maximize it.The key to manifest F-C mechanics is to seek out the maximum one among F-C factors and analyze the dynamical behaviors of the system through the properties of the F-C factors.
Recently a system of central spin with coupling to the environmental spin-spin interaction has been studied to show the FC principle.[9]Dynamics of this model are also well investigated to show the F-C effect in some realistic systems such as quantum dot(QD).[10−14]Meanwhile by means of F-C principle we could understand better the dynamical transition process of the coupled systems.In general,the systems in previous research are all featured by a simple collective environmental spin chain or vibrational mode coupling to a central two-level system.It is well known that the environment consisting of many non-interacting spins can not manifest the macroscopical nature since the order parameter can not appear in such system.[15]To consider the role of macroscopical nature in decoherence central spin,we study the dynamical behaviors of a central spin system coupling to an Ising chain in transverse field near the critical point.
Quantum critical phenomenon is a main subject for recent years in both theoretical and experimental physics.The quantum critical system can demonstrates a quantum chaotic effect when QPT happens.In this paper,we study a quantum critical system from the perspective of Franck-Condon principle by using the central spin as a probe.We consider what will take place when a central spin is excited in environment of an Ising chain in transverse field.[16−17]Some theoretical predictions[18−22]and experiments[23−25]verified that the central spin can be used as a probe to examine the super-sensitivity of the quantum critical or quantum phase transition system.The F-C principle will provide us such a way to carefully investigate the underlying physical mechanism of quantum critical system,since the change of energy configuration and the wavefunction overlap in the transition process are the main subjects of F-C principle.And we can analyze how the transi-tion probability are related to system’s parameters such as dimension,coupling constant,and critical value of the system.
Our model is considered as a central spin immersed in an environment of Ising spin chain in transverse field,which is similar with Hepp-Coleman(HC)[26−27]model for quantum measurement.This central spin could be modeled as an electron spin or another two-level system.We assume that the central spin is initially polarized in the z direction as a measuring apparatus.The Ising spin-1/2 ensemble in a transverse field is dispersively coupled to the central spin in the z direction with highly simplified dipole-dipole interaction. Essentially,different centralspin states result in two different effective Hamiltonians of the Ising spin chain,which can be respectively diagonalized as its two collections of fermionic modes.The F-C factors as overlap integrals are constructed by a series continuous multiplying trigonometric function about Fourier-transform vectors k.The F-C factors around the critical point have many distinctive properties that relate to the super-sensitivity and chaotic behaviors.The overlap integral of F-C factors is also evaluated by two collective rotated spin states.However,every rotated angle depends on function of parameters of system,which is equivalent to the results obtained by the direct deionization method.From the rotated spin picture,the chaotic properties of quantum critical system are intuitively demonstrated.Considering the time evolution and the Lorentz absorption spectrum[28]of the central spin system,the distribution of the relative transition intensity is obtained as a function proportional to the F-C factors.Several papers[18,29]have investigated Ising model in transverse field through Loschmidt echo or correlation spectrum.With the F-C principle,we can find the most possible transition,which has the maximum F-C factor.At zero temperature,the Lorentz absorption spectrum splits into several small peaks around the critical point,and every peak is sensitively affected by the parameters of system.The sensitive behavior around the critical point is well understood since the F-C factors are continuous multiplying of monotonic function in dioganolized Fouriour-transform k space.
This paper is organized as follows:In Sec.2,we present our model as an Ising model in transverse field coupling to a central two level spin and dioganolize it into two effective Hamiltonians.In Sec.3,from the perspective of F-C principle,the maximum F-C factor around the critical point is found to anylise the transition process.In Sec.4,we present a rotated spin picture to describe the supersensitivity and chaotic property of the quantum critical system and verify that the result is equivalent to that in Sec.2.The absorption spectrum is evaluated in Sec.5 to demonstrate how the dynamical behavior of this critical system is affected by F-C factors and its peaks and supersensitivity can be explained by F-C principle.In Sec.6,we conclude.Some detailed calculation about F-C factors are given in the Appendix.
2 Model Setup
Our model is set up as a central two-level spin immersed in a Ising spin chain in transverse field,where the chain satisfies the Born-Von Karman boundary condition hypothetically.The central spin coupling the spin bath is polarized in the z direction and is prepared in its ground state(the spin-down state).The nearest neighbor interaction of j-th and(j+1)-th spin along x direction is of an Ising type in transverse field.The corresponding Hamiltonian reads as
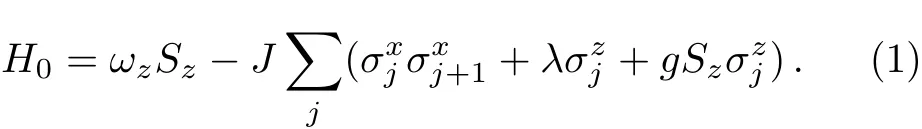
It is well known that λ=1 is the critical point of the Ising model in transverse field,the coupling g here is significant “small” comparing with λ =1 to guarantee that λ+g is still near the critical point 1.We set J=1 as a normalized coefficient,which characterizes the nearest neighbor interaction for convenience.In order to probe the absorption spectrum of central spin,we apply an external oscillated transverse driving magnetic field.This transverse field is coupled to the central spin Sxin the x direction which described by

The transverse coupling is weak comparing the coupling in the z direction,thus Ω ≪ ωzso that the perturbation theory can be applicable.At zero temperature the oscillated transverse driving filed excites the central spin from its original spin-down ground state to spin-up excited state,and the co-excited Ising spin chain vibrates from its initial ground state to one of its excited state,too.
The Hamiltonian H0can be diagonalized in its direct product Hilbert space as:⊗ |sz〉〈sz|,where sz= ±1 is the eigen value of the central spin Sz.Hereis the reduced Hamiltonian with the central spin at state|s〉and reads as
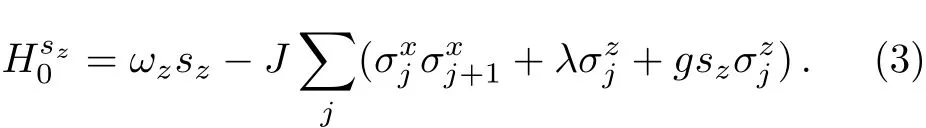
By the transformation corresponding to different subspace|±1〉with two denoted operators defined as
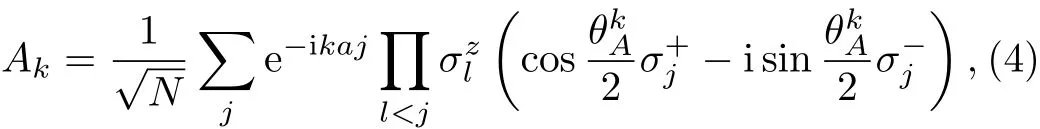
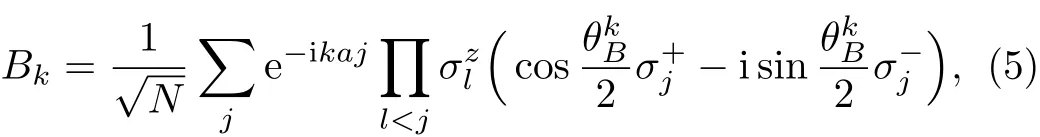
where the angle is separately decided by
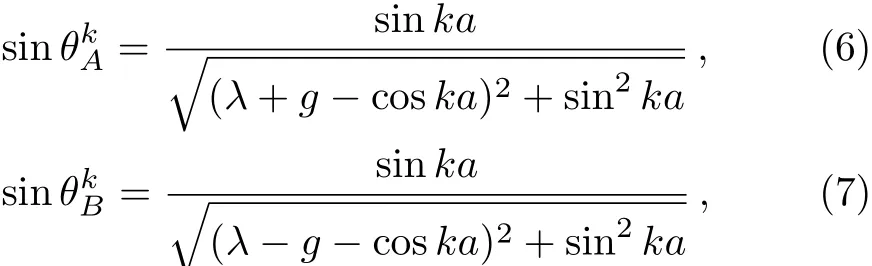
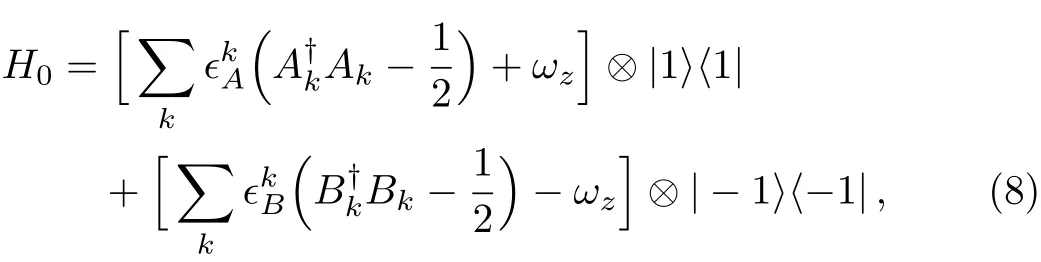
and the energy spectrum about k is separately denoted by
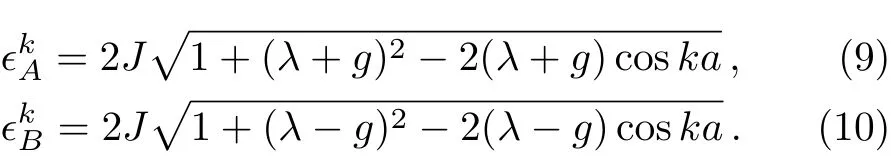
The operators Akand Bkare the canonical anticommutation fermion-like operators which satisfy:

and they are connected by a rotation relationship:
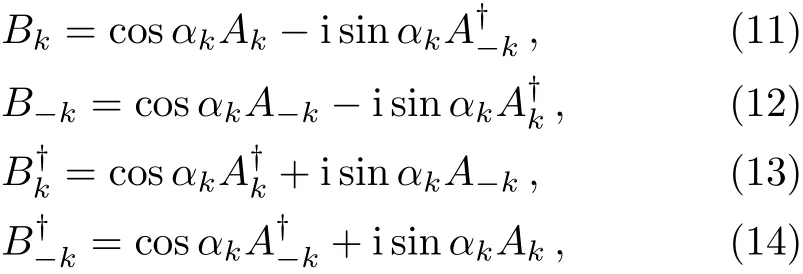
where αk=(−)/2,and cosα−k=cosαk,sinα−k=sinαk.The descrete k in momentum space is

with N sites of the spin chain.Now the original Hamiltonian is diagonalized into two sub-pace:

The ground energy of H−is
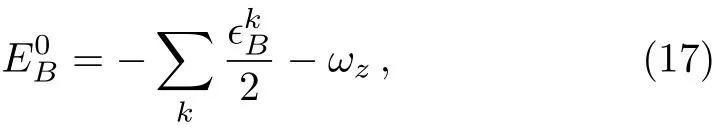
and the ground state energy of H+is:

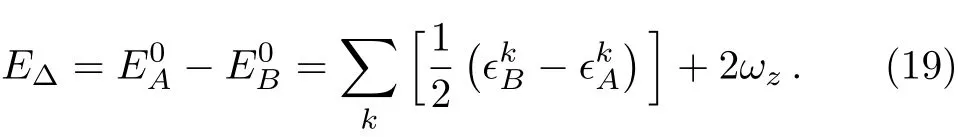
Until now we have diagonalized the H0into fermion-like representation,and the eigen states are a series direct products of|0〉kor|1〉kfermion-like excitations about k mode.In Fig.1 we see that around the interval of(λ−g,λ+g),the transition probability amplitude is depressed deeply.
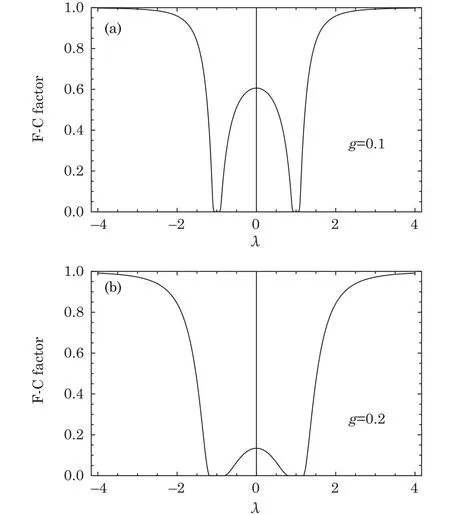
Fig.1 (a)F-C factor between two ground states when g=0.1,N=200.(b)F-C factor between two ground states when g=0.2,N=200.
3 Maximum F-C Factors Related to Parameters of System
We assume that the system is initially prepared on its ground state|0〉B⊗|s= −1〉,where the temperature is set at zero Kelvin for a consideration of completely quantum effect.The time evolution of the system is started when the central spin is excited from its initial ground state(spin-down)to the excited state(spin-up)by a probe field HI= ΩSxcosωt.Meanwhile the whole system is transformed to its whole ground state to one of its co-excited state.The system is diagonalized by two direct product basis:|nk〉⊗ |s=1〉and|mk′〉⊗ |s= −1〉,where the|nk〉(|mk′〉)represents an n(m)excitations in the k(k′)mode and every excitation is occupied with one fermion at most,i.e.nk(mk′)=0,1.
We assume that the system initially prepared in the ground states of H−:|0〉B.The ground state|0〉Bis obtained by the annihilation operator BkB−kacting on the ground state|0〉Aof H+:

The matrix elements of transition possibilities can be calculated by the corresponding way
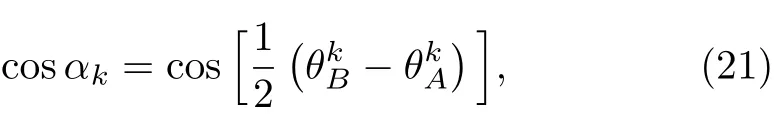
where C is a normalized factor that can be evaluated.This formula is evaluated by Bogolyubov transformation.The ground state of H−is spread over the eigen states of H+by a series coefficients cosαkand sinαkabout k.Considering the perturbation interaction of HI,when the central spin Szis excited by this perturbation from spin down to spin up,the sub Hilbert space is transferred from B-denoted space to A-denoted space.The energy level of whole system state is transformed from the initial ground state to one of eigen vibrational level.There are always a pair excitations on k and−k modes.F-C factors here are defined as transition matrix element of different eigen energy levels.These elements can be evaluated at once to anylisis the transition space of two.For example, firstly from ground state of H−to ground state H+,the transition matrix element is
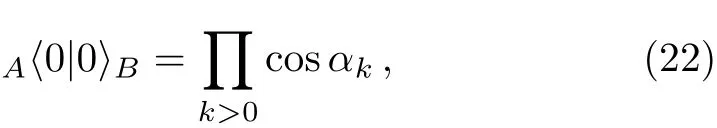
secondly from ground state of H−to full excitations of H+,the element is
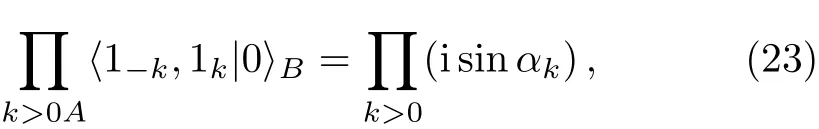
thirdly from ground state of H−to one specific k′,−k′pair of excitation of H+,the element isA〈1−k′1k′|0〉B=isinfourthly from ground state of H−to two specific k′,−k′and k′′,−k′′pairs of excitation of H+,the element isA〈1−k′1k′1−k′′1k′′|0〉B=isin αk′isinThe transition possibility of ground state of H−to n excitations of first several k of H+reads
According to Ma, studies of panguite and other newly discovered refractory minerals are continuing in an effort to learn more about the conditions under which they formed and subsequently evolved. Such investigations are essential to understand the origins of our solar system, he says.
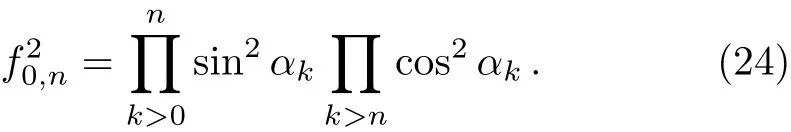
It directly follows from coska= −cos(π −ka)that we theoretically prove thatand for one excitation there isWe now give some plots about these F-C factors depending on λ and g:
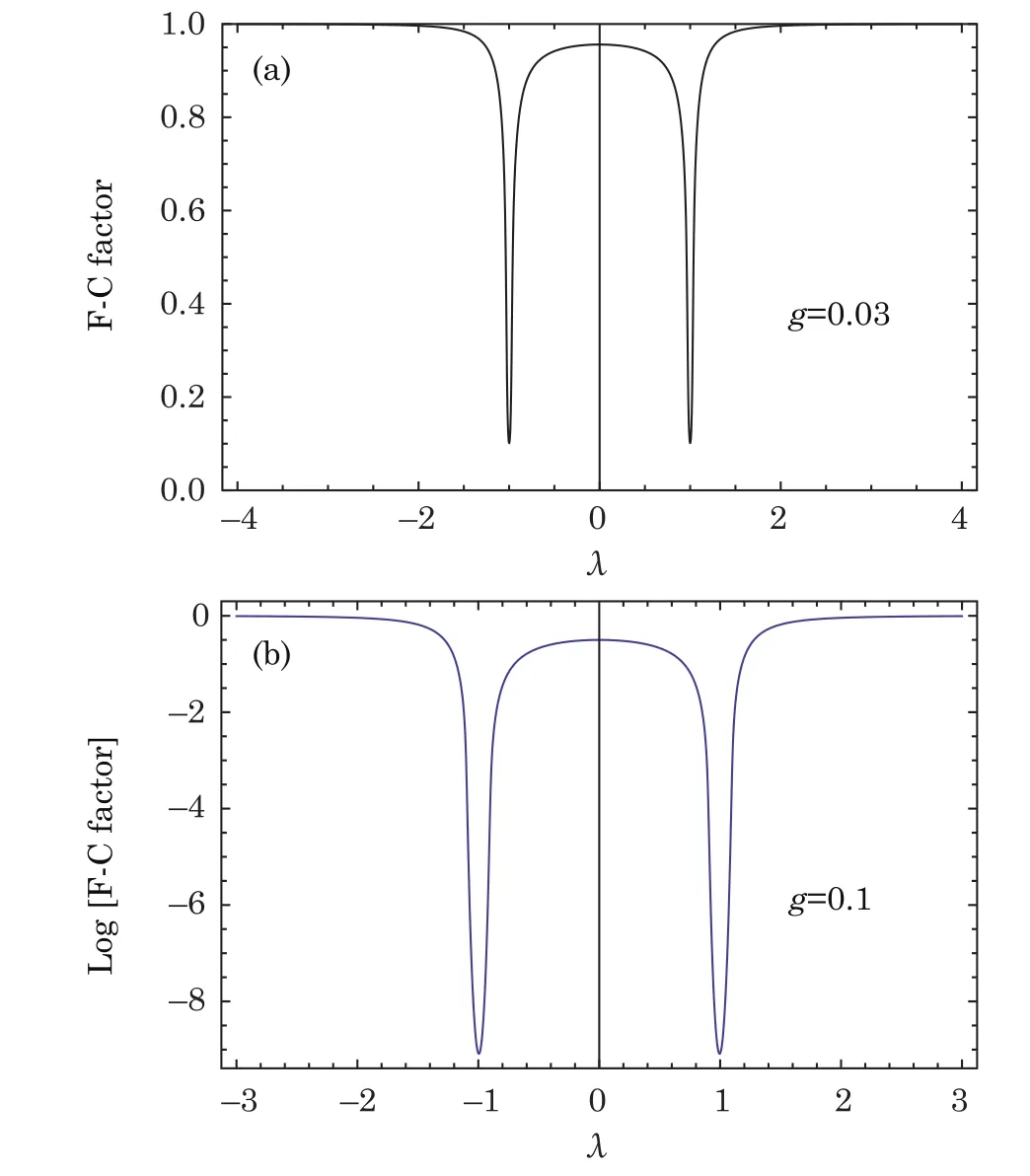
Fig.2 (a)F-C factor between two ground states when g=0.03,N=200.(b)Logarithm of F-C factor between two ground states when g=0.1,N=200.
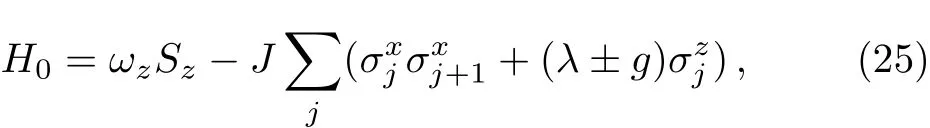
It is observed from Figs.1 and 2 that around the critical point λ =1,λ ± g in fact characterizes the quantum phase transition area.Since in reduced Hamiltonian the nearest neighbor interaction strength λ±g competing with the z direction interaction strength 1.And in the area of this phase transition,the F-C factors of two ground states are deeply depressed from 1 and meanwhile the other factor are inevitably excited instead.The logarithm of F-C factor of λ=1,g=0.1 shows that in the phase transition area the depressed F-C factor is about an exponent function about λ+g.This can be theoretically proved by an approximation evaluating.
The behavior of F-C principle can be used to understand the transition possibility of H−to H+.The reduced Ising chain in transverse field are an exactly solvable model.The factors are a series continuous multiply of coefficient about k.Around the critical point of λ=1,the energy level are very dense and the chaotic properties are demonstrated in many ways.But by the analysis of F-C factors we are still able to find the mathematical rule of transition possibilities around the critical point of phase transition λ=1.
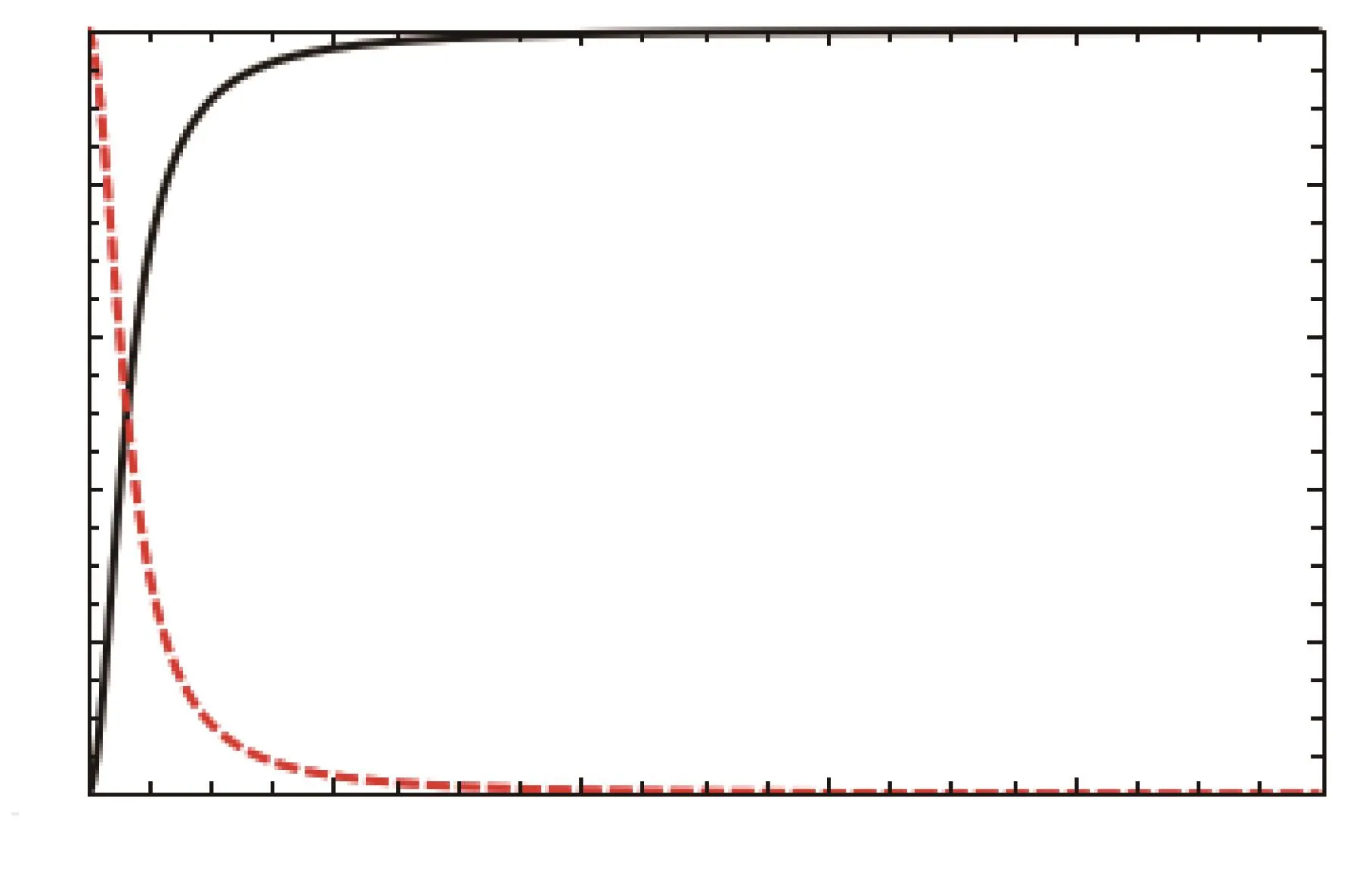
Fig.3 Monotonicity property:terms of F-C factors cosαkand sinαkversus kn.
As shown in Fig.3,the good properties of F-C factors around the critical point of λ=1 is that the F-C factors of cos2αkare monotonic increasing and sin2αk=1−cos2αkare monotonic decreasing versus kn=(n−1/2)2π/N,n=1,2,...,N/2.From the expression of F-C factors
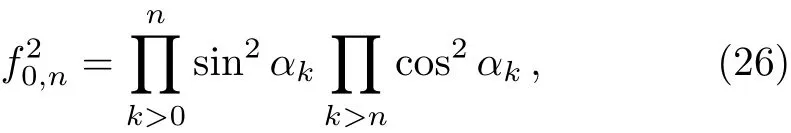
we see that for specific excitation numbers the excitation of first several k always is the maximum F-C matrix element.The proof of this conclusion are presented in the Appendix A.This mathematical properties about F-C factors around the critical point can be well understood according to the analytical calculation:since the Ising model is an absolutely solvable question,the cosαkterms and sinαkare competing with each other to decide the maximum F-C factor as the coefficient λ±g competing with 1.But this“competing” is taking place in the momentum k space so that we could see the detailed process depending on parameters.Around the critical point the first several k excitations having the maximum factor for specific excitation numbers.
Going a step further we only need to find which excitation numbers have the maximum factor.Setting the first q excitations of k space having the maximum F-C factors,we solve this inequality to seek out the maximum F-C factors:

We get that
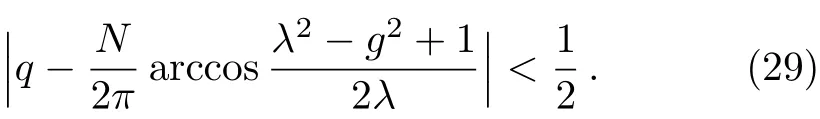
This inequality clearly shows that the transition possibilities are how sensitive to the system parameters,since around the critical point λ=1,the specific excitation numbers q changes sensitively depending on system’s parameters of N,g.
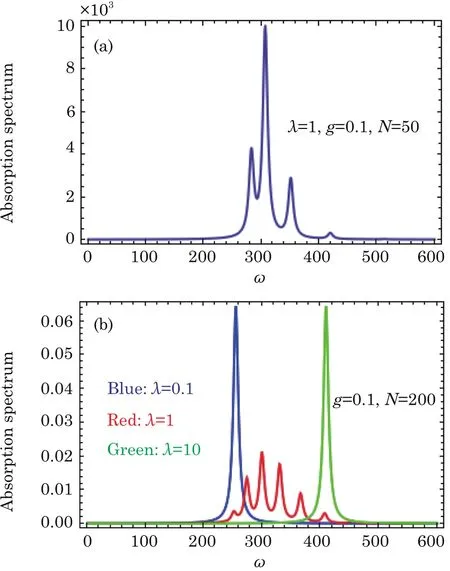
For example,we make that N=200,λ=1,g=0.1,thus we get 2.684 43 The Hamiltonian H0can be diagonalized as a series product of fermions.These fermions behavior as the spin 1/2 particles since they have the two energy levels.The well-known Jordan-Schwinger transformation transforms the fermions to spin 1/2 particle as: and this Hamiltonian can be diagonalized as a series summation of rotated spin 1/2 particle by where the energy spectrum of H0is The rotated angle is defined as Then this Hamiltonian is diagonalized through the Pauli Matrix where αk=(−)/2.We have obtained the same results with Eq.(22)in the previous section.The rotated spin picture tells us that the F-C factors are like a series complication of cosine of every rotated angle.Around the critical point the F-C factors are seemingly chaotic,but from the last section we know that there are maximum FC factor and how the factor is related to the parameters of system. By considering the external drive HIas a perturbation,the total wave function of the system at time t is obtained as where csmis the probability amplitude of system staying at state of|m,s〉,m is the m excitations in k space and s is the eigen state of Sz.Substituting|ψ(t)〉into the Schrodinger equation,we get Then we apply the perturbation theory up to the first order approximation for the system is initially prepared at the ground state,i.e.,csm(t)=csm(0)= δs,−1δm,0.By assuming the perturbation H1= ΩSxcos(ωt)to the system,we apply that Ω≪J so the first order perturbation approximation is guaranteed to a high accuracy.Then the probability amplitude of different energy level at time t is obtained as Thus the probability on the state|s=1,n〉at time t reads as According to the well known Fermi’s golden rule,the transition rate of the spin chain from initial ground state|0,s= −1〉to the final state|n,s=1〉in the long time limitation is evaluated as where the mathematic limitation: is used.Summing up the transition rates over all the possible final states,we obtain the absorption spectrum: This is a summation of n terms proportional to F-C factors.We phenomenologically introduce the decaying factor exp(−Γt)in the quasi-mode treatment of dissipation The Delta spectrum shapes reduce to the Lorentzian spectrum shapes: We have numerically plotted this Lorentzian type of absorption spectrum to show that the spectrum mainly depends on F-C factors around the critical point. Fig.4 (Color online)(a)Lorentzian type absorption spectrum when N=50,g=0.1,λ=1.(b)Lorentzian type absorption spectrum when N=200,g=0.1,and λ=0.1(Blue);λ=1(Red);λ=10(Green). As shown in the Fig.4,the Lorentzian absorption spectrum of N=50 has the maximum peak at about first 1k excitations corresponding the F-C factor of N=50;when N=200,λ =0.1 and λ =10,the spectrum only has one peak since only the excitation between ground states is important.But at the phase transition area the absorption spectrum are multi-peaks and the maximum peak is at 3k corresponding the factor of N=200.In a word,the spectrum and F-C factors are mainly depended by N,λ,g and around the critical point system runs into phase transition and turns sensitively depending on N,λ,g.Di ff erent peaks about absorption spectrum re flects these properties and shows the identical to F-C factor’s properties. We have studied the role of F-C principle for the dynamical sensitivity of an Ising model in transverse field in response of the motion of the central two level spin.The F-C factors of this system are obtained as a product of a cosine-and sine-function series about parameters in momentum k space of the coupled system.According the monotonic property of these cosine and sine functions,we carefully analyze how transition possibility sensitively depends on the parameters of the central spin system,e.g.,the dimensional N,internal coupling strength g and order parameter λ.The time evolution of system are evaluated to obtain the absorption spectrum,which is also proportional to the F-C factors.The peaks of the absorption spectrum can be explained by the characters of F-C factors,which are sensitively affected by parameters of system around the critical point.With these tries the super-sensitivity of quantum critical system around critical point is understood from the perspective of Franck-Condon principle. Acknowledgments We are thankful for the discussions with C.P.Sun and Y.N.Fang. Appendix Now we focus on the phase transition area λ=1.For the derivation of(a=1) That is to say cos2αkare monotonic increasing and sin2αk=1− cos2αkare monotonic decreasing versus kn=(n−1/2)2π/N,n=1,2,...,N/2. I.e.we always have Next we firstly prove that in specific excitation numbers,the first several k excitation have the maximum FCs.For one excitation, when k′ For two excitations,where we make the notation that kn=kn=2π/N(n−1/2),n=1,2,...,N/2. When m 6 l,n Thus A s the same progress,for specific excitation numbers,the first several k excitation always is the maximum F-C matrix element. Now we find out the maximum FC among these different excitations situations:(where we make the notation that αkn= αn) We know that cos2αkare monotonic increasing and sin2αkare monotonic decreasing.Thus when are both satisfied,we get that the corresponding q excitations have the maximum FC. We evaluate that We are thankful for the discussions with C.P.Sun and Y.N.Fang.4 Rotated Spin Picture
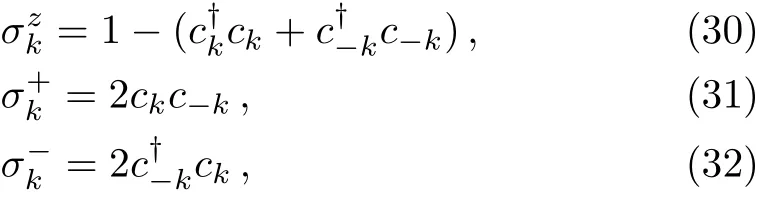
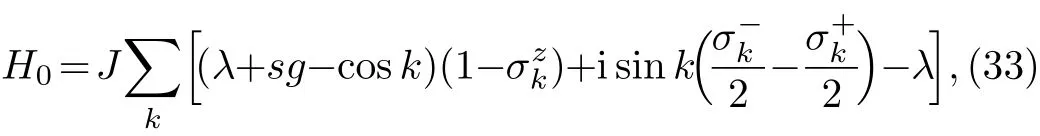
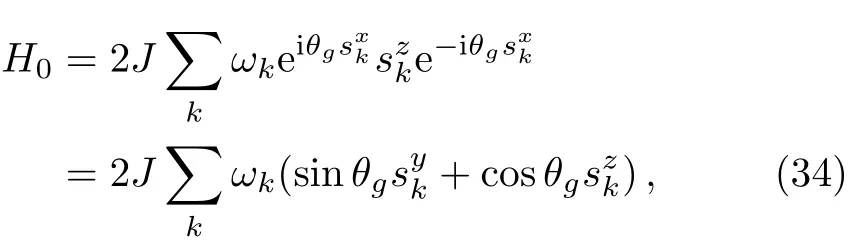
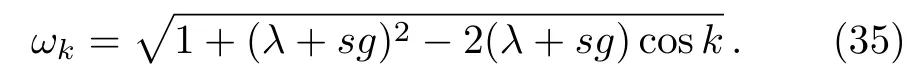
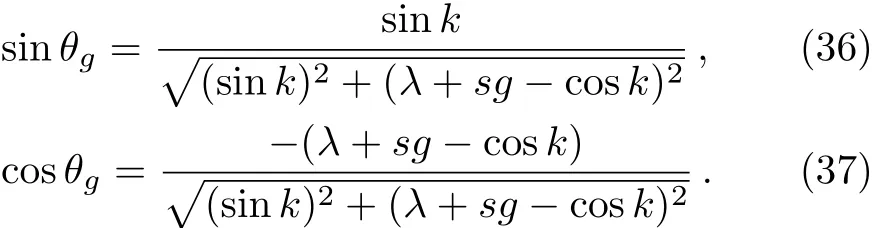
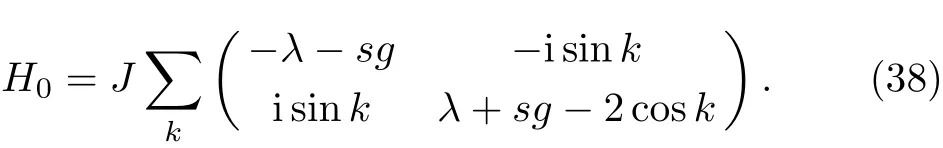

5 Transition Rate and Absorption Spectrum Around the Critical Point
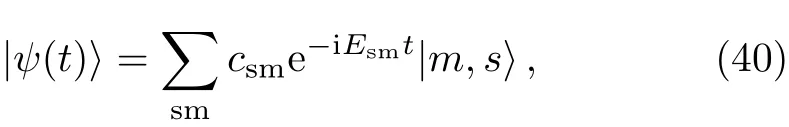
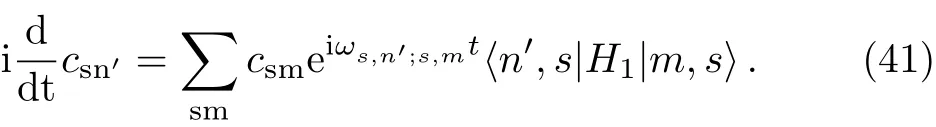

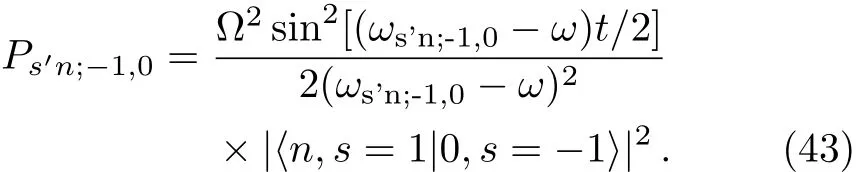
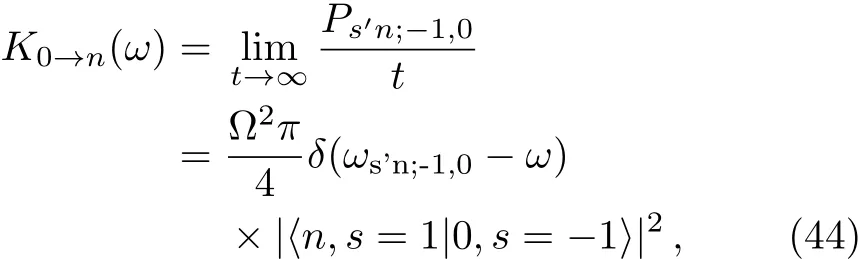
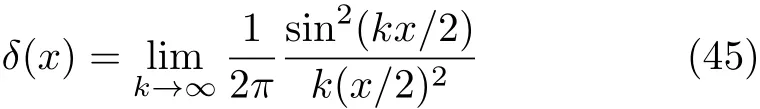
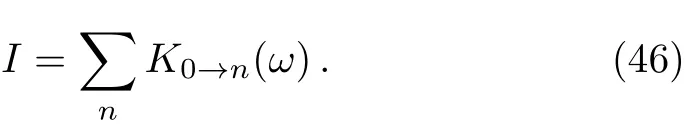
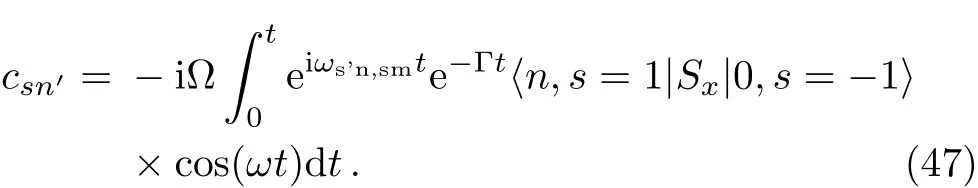
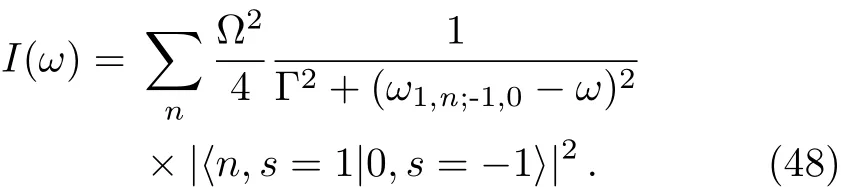
6 Conclusion
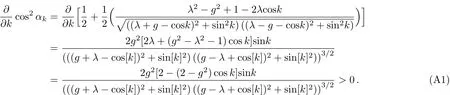

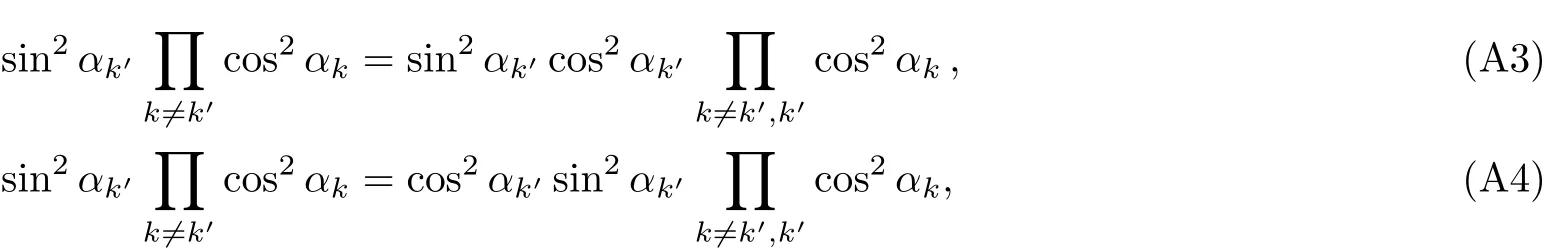
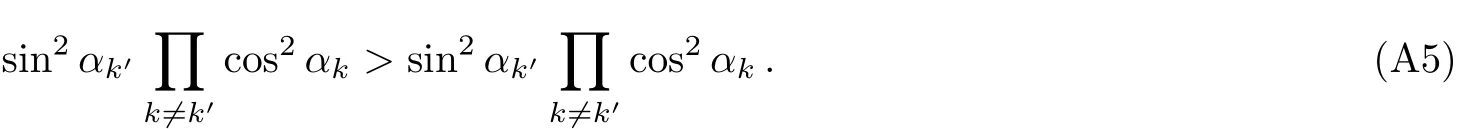
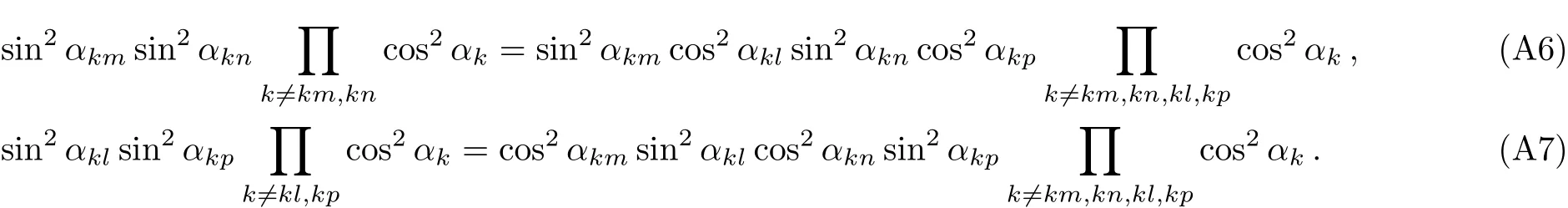
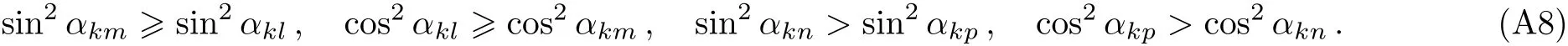
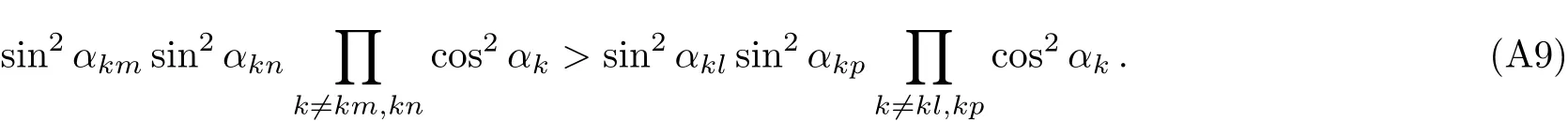
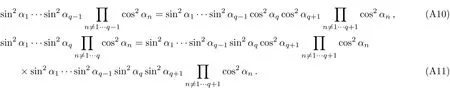
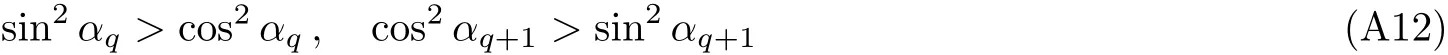

7 Acknowledgments
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
