Dipole Polarizabilities of the Ground States for Berylliumlike Ions∗
Chao Chen(陈超) and Bing-Cong Gou(苟秉聪)
School of Physics,Beijing Institute of Technology,Beijing 100081,China
AbstractDipole polarizabilities of the ground states for berylliumlike ions with nuclear charge Z=4 to 10 are calculated by using the Rayleigh-Ritz variational method with multiconfiguration interaction wave functions.The representative models of convergence are listed and compared with other theoretical data for nuclear charge Z=4 to 6.The present dipole polarizabilities are in good agreement with previous accurate theoretical values available in the literature.For results with greater nuclear charge number,the present calculations may provide benchmarked data for future theoretical and experimental studies.Dynamic dipole polarizabilities of the ground state for the beryllium atom at selected frequencies are also calculated and compared with other theoretical values in the literature.
Key words:dipole polarizability,berylliumlike ions,variation-perturbation method
1 Introduction
The dipole polarizability is the lowest order response of the electron charge distribution to an external electric field,and it also plays an important role in studies of electron-atom scattering,ion mobilities in gas,Rayleigh scattering cross sections and various phenomena induced by intermolecular forces,etc.[1]The dynamic multipole polarizability at imaginary frequency can be used to calculate the dispersion coefficients for the long-range interactions among atoms.The dynamic polarizability also determines the linear response of a quantum system to a monochromatic perturbation with frequencies. The tune-out wavelength is defined as the wavelength,which makes the dynamic multipole polarizability of a single state disappear.[2−4]The study of tune-out wavelength is also very important from experimental side.The precise wave functions and energies can be used to get the high accuracy of frequency dependent dynamic dipole polarizabilities to be retained for frequencies far from zero.[5]The precise calculation of the dipole polarizability can be used as a good test of the any many body theory;it can be also used to research the potential interactions of electron correlation effects in the measurements at the same time.Polarizabilities are also useful quantities in the theoretical description of interatomic interactions and optical properties of materials.[6]
There are growing need of studies on berylliumlike systems owing to the recent progress in the field of ultracold atom physics,new-generation frequency standards,and optical lattice clocks.[7−8]Various sophisticated experimental techniques have been used to measure polarizabilities in different atomic systems,but there are also some systems where no experimental results are yet available such as berylliumlike systems.There have been some theoretical investigations of polarizabilities of berylliumlike systems in the literature,which mainly focused on systems with smaller nuclear charge number.[9−27]Although dipole polarizabilities for the ground states and fewer lowlying excited states of berylliumlike systems have been calculated,to our knowledge,less attention has been paid to dipole polarizabilities of berylliumlike systems with greater nuclear charge,so the research from the theoretical aspect is very significant.
In this work,the Rayleigh-Ritz variational method with multiconfiguration interaction wave functions[28−29]are used to calculate the dipole polarizabilities of the 1s22s21S ground states of berylliumlike systems with Z=4 to 10.For berylliumlike systems with Z=4 to 6,the representative models of convergence of the dipole polarizabilities are analyzed,and while these polarizabilities will be compared with other theoretical values available in the literature.For berylliumlike ions with Z=7 to 10,our predictions may provide valuable reference data for other research in the near future.Dynamic dipole polarizabilities at selected frequencies of the ground state for the beryllium atom are also calculated finally.
2 Theory
The non-relativistic dipole polarizability of the atomic system is given in the LS coupling scheme as

where the ground state wave function is Ψ0,the corresponding eigenvalue is E0.The first-order wave function Ψ1can be obtained from the following first-order pertur-bation equation

where H0is the unperturbed Hamiltonian,and dipole eigenvalue E1can be calculated by
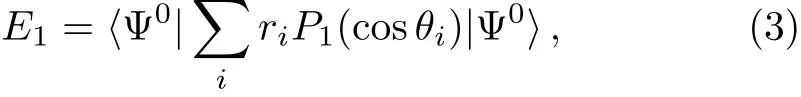
Using Dalgarno-Lewis variation-perturbation method,[30]Eq.(2)can be solved by minimizing the function
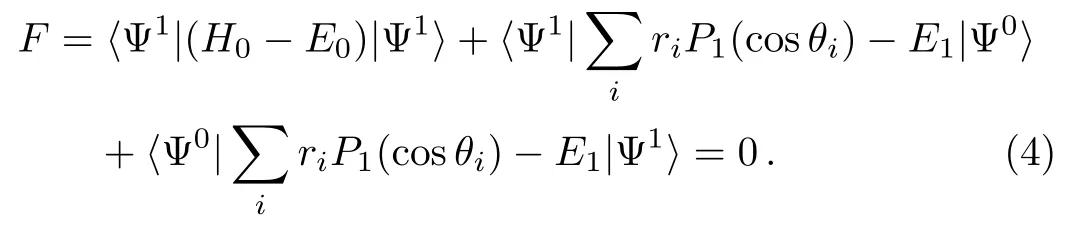
Although the summation in Eqs.(1)–(4)should extend over all P states having parity opposite to the ground state,including the continuum,in practice;most of the contributions come from those states lying close to the ground state because of the energy denominator.In this case,the contribution from the 2s2p1P state will contribute most part of the dipole polarizability.Therefore the calculation of polarizabilities should be restricted to consideration of a finite number of terms in the sum over intermediate states,neglecting the contribution of the continuous spectrum.As discussed previously,polarizabilities can be calculated using direct numerical integration of the Schrödinger equation,adding the perturbation operator to the atomic Hamiltonian through Dalgarno-Lewis variation-perturbation method.The zeroth-order degeneracy is omitted in the calculation of dynamic polarizabilities,but the requirement of a smooth continuation to the static limit needs to be respected.[31−33]
In this work,the wave functions for berylliumlike ions can be expressed as

where A is the antisymmetrization operator,and Slater orbitals are used to construct the radial basis function
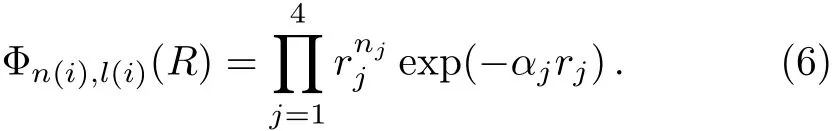
The angular wave functions are expressed as
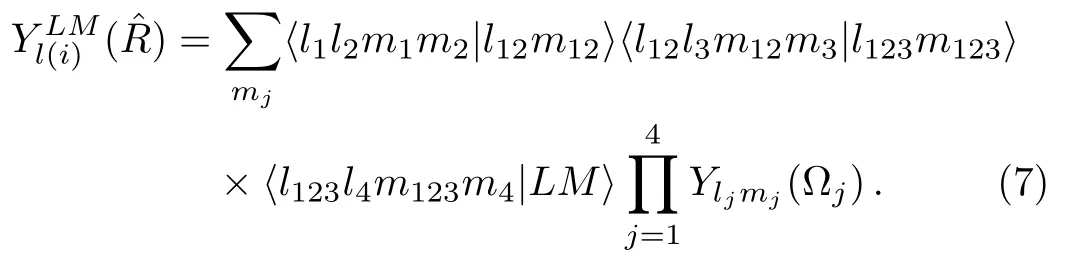
The angular coefficient can also be simplified as

where l1and l2couple into l12,l12and l3couple into l123,finally,l123and l4couple into the total orbital angular momentum L and azimuthal M.The spin wave function can be expressed as
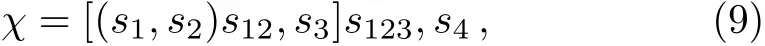
where s1and s2couple into s12,s12and s3couple into s123, finally,s123and s4couple into the total spin angular momentum S.
The basic wave functions and the energies of the 1s22s21S ground states for berylliumlike systems are obtained by using the Rayleigh-Ritz variational method.The firstorder wave function Ψ1in Eq.(2)is a wave function of the P symmetry,which can be also constructed by a CI basis set from Eq.(5),and the difference is displacing the wave function described in Eq.(5)from the S symmetry to the P symmetry.By optimizing the function F in Eq.(4),all the linear parameters in these P symmetry wave functions are obtained.For angular and spin wave function in Eq.(5),all possible l(i)and χ are tried and keep the ones which make significant contribution to the dipole polarizability.
3 Results and Discussions
For the 1s22s21S zeroth-order wave functions of berylliumlike systems,the number of linear parameters in the Ψ(1,2,3,4)of Eq.(5)changes from 830-894,and the number of angular-spin components changes from 52 to 65 to obtain accurate wave functions.The convergence of the dipole polarizability α1(0)is very fast when basis functions Ψ1are chosen well during the course of optimizing the function F in Eq.(4).For the first-order wave function Ψ1,the number of linear parameters in the Ψ(1,2,3,4)of Eq.(5)changes from 151-305,and the number of angularspin components changes from 9 to 20.
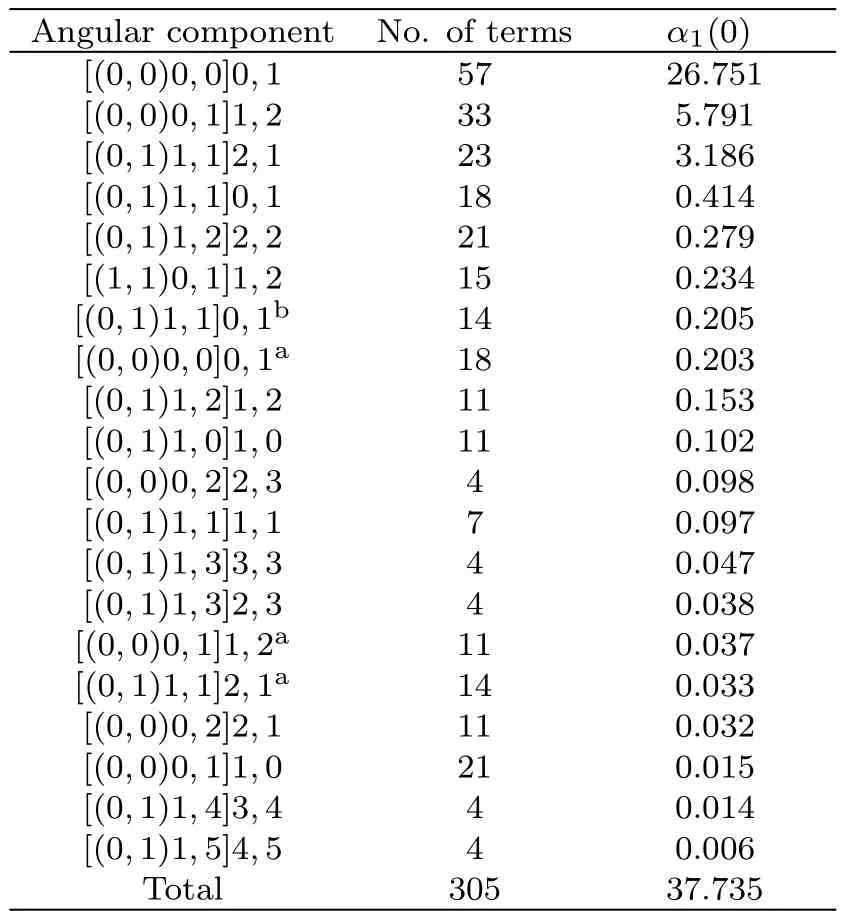
Table 1 The convergence pattern of the dipole polarizability α1(0)of the ground state for the beryllium atom.(in a.u.)
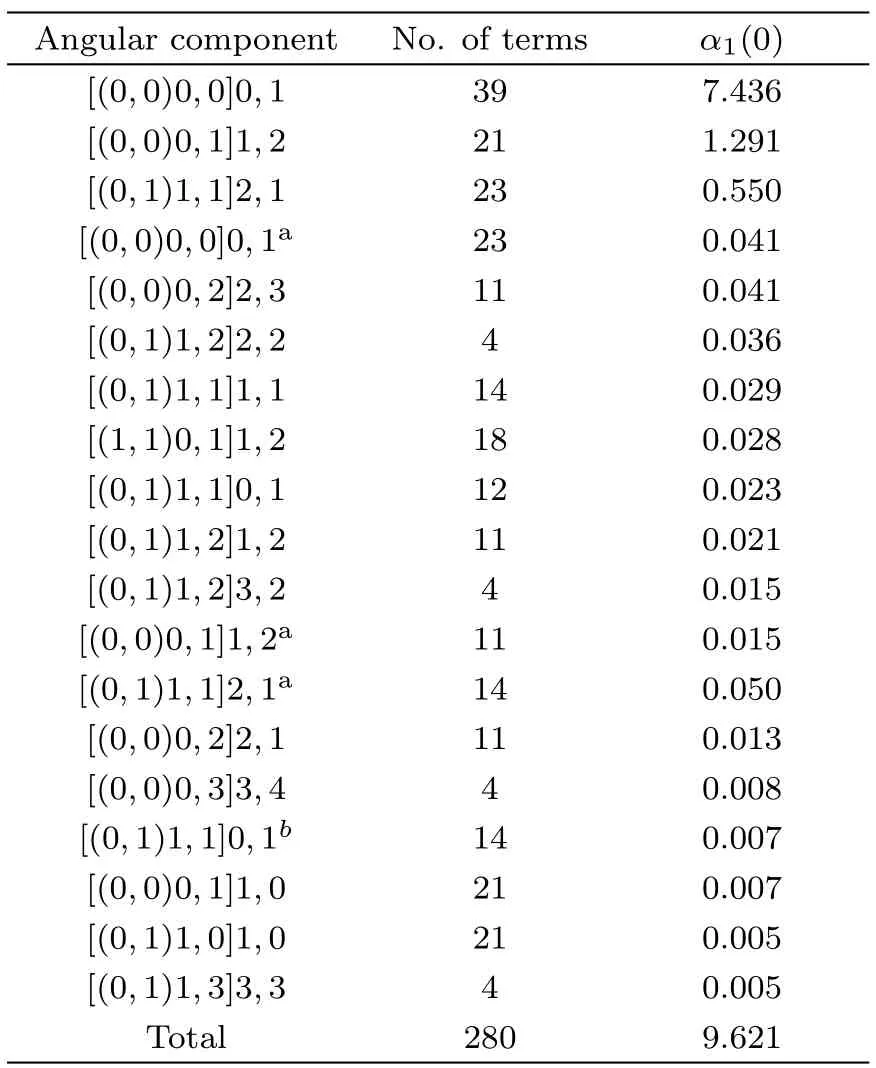
Table 2 The convergence pattern of the dipole polarizability α1(0)of the ground state for the the B+ion.(in a.u.)
For the accurate calculation of polarizabilities,the electron correlation should be fully taken into consideration. The detailed convergence model studies of the dipole polarizabilities for the 1s22s21S ground states of the berylliumlike systems with Z=4–6 are listed in Tables 1–3.It is easily seen that their convergence are very fast.The convergence model of dipole polarizabilities for the angular component is similar for each berylliumlike system.The most important contribution to the dipole polarizability all comes from the[(0,0)0,0]0,1 component;the contribution percentages for Be,B+,C2+are 70.89%,77.29%,and 64.04%,respectively.The lower angular components contribute much more than the higher angular components.For the dipole polarizability of the ground state for the beryllium atom,the important angular components are[(0,0)0,0]0,1,[(0,0)0,1]1,2,[(0,1)1,1]2,1,and[(0,1)1,1]0,1,etc.The angular components are fully saturated in the variational calculation of dipole polarizabilities,especially for the greater contribution percentage components.
To the best of our knowledge,the most extensively studied dipole polarizabilities of the ground states for berylliumlike systems in the literature is the neutral beryllium atom,while the studies for other berylliumlike ions are scarce especially for nuclear charge numbers Z>6.The present results are compared with values from literatures in Table 4.All the reference data are listed in this table with the information of calculation methods.For the neutral beryllium atom,the present result is in good agreement with later theoretical results and excels earlier results in precision.It is 0.02 a.u.less than the exact value using a basis of explicitly correlated Gaussians(ECGs).[21]Similarly,the relativistic configuration interaction plus many-body perturbation theory(CI+MBPT)values[22]is 0.025 a.u.greater than the present calculation.The present dipole polarizability agrees with the value from the configuration interaction method considering a semi-empirical core-polarization potential(CICP)[24]to all the four effective figures.For the B+ion,the present dipole polarizability agrees with the value from the CICP method[25]to the second effective figures.The present value locates among three results obtained from three different methods,namely,CI,CI+MBPT,and CI+allorders by Safronova et al.[23]In particular,the present calculation is only 0.003 a.u.less than the exact value from the CI+all-orders method mentioned above.For the C2+ion,there are only two reference data in the literature.The present dipole polarizability locates between two theoretical values from the coupled Hartree-Fock method[9]and the singly and doubly approximated coupled-cluster methods at the nonlinearized theory(CCSDpT).[27]However,the CCSDpT results in Table 4 seem to be greater than all the other theoretical values.The differences in these CCSDpT results are explained mainly due to inclusion of the pair-correlation effects to all orders in their coupled-cluster method in Ref.[27].
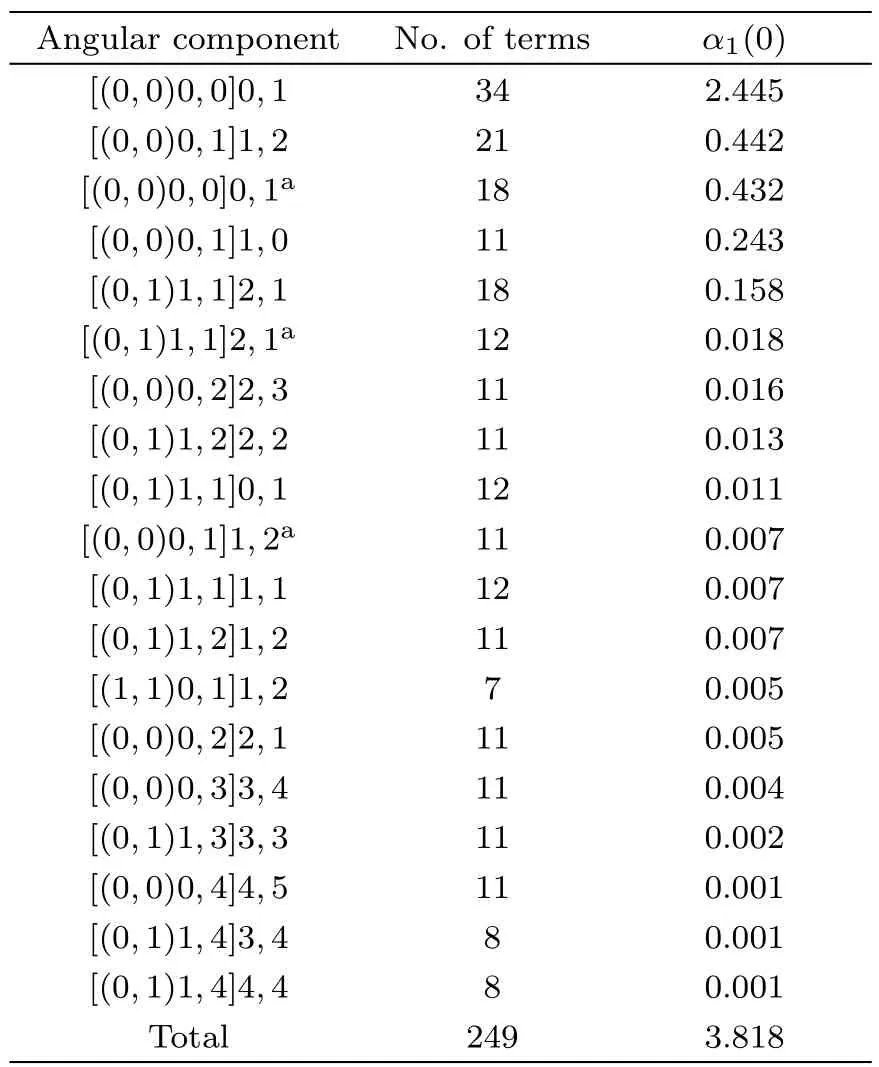
Table 3 The convergence pattern of the dipole polarizability α1(0)of the ground state for the the C2+ion.(in a.u.)
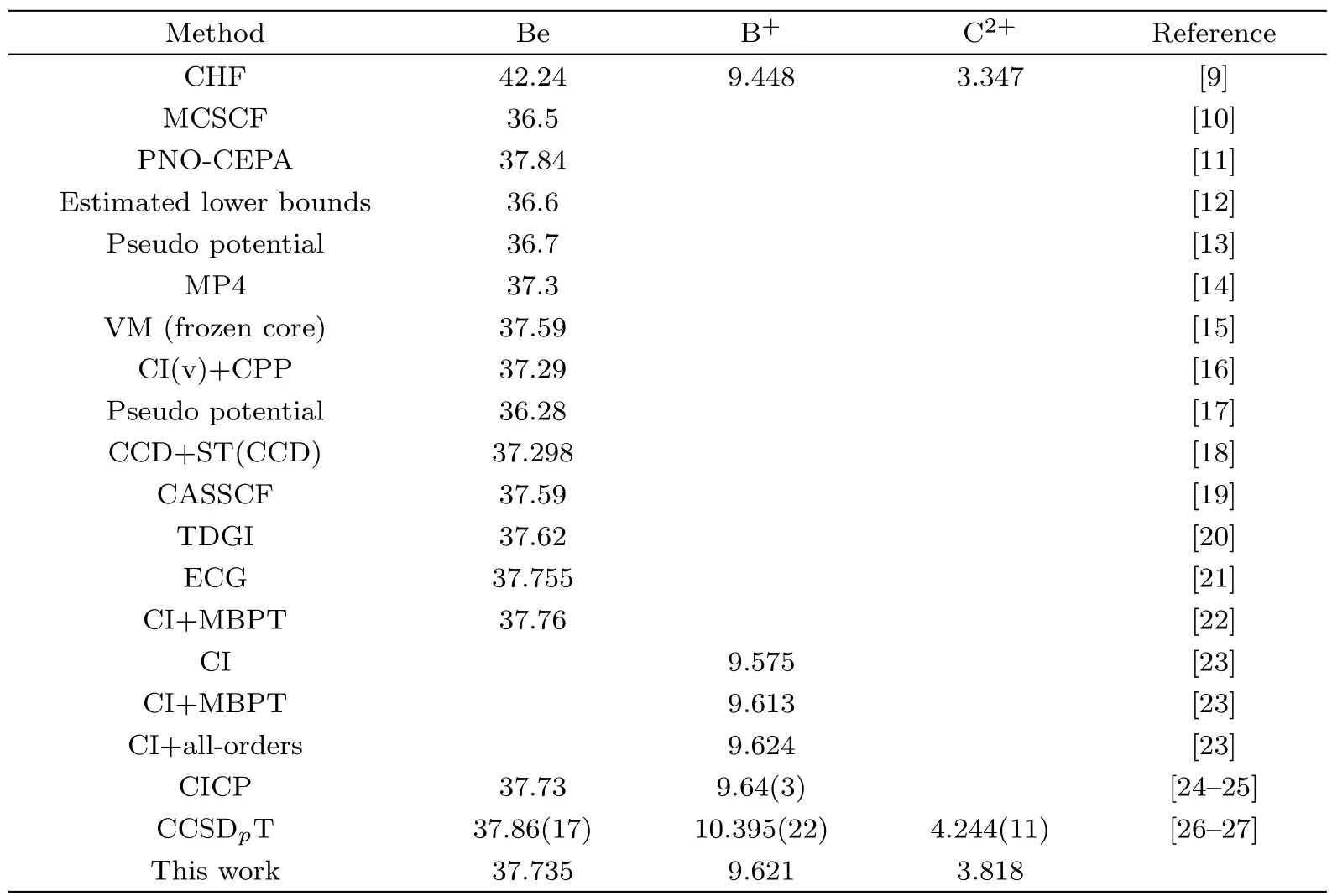
Table 4 Comparisons of the dipole polarizabilities of the ground states for berylliumlike ions from different theoretical methods.(in a.u.)

Table 5 The convergence pattern of the dipole polarizability α1(0)of the ground state for the the N3+ion.(in a.u.)
The information on dipole polarizabilities of berylliumlike systems with Z>6 is rather scarce in the literature,so the list of these reliable values from the present calculation is significant.The dipole polarizabilities of the ground states for berylliumlike systems with Z=7 to 10 are listed in Tables 5–8.The coulomb interaction between nucleus and electrons becomes more intense and the response of the electron distribution to the electric field gets weaker with the isoelectronic sequence,so dipole polarizabilities decrease with the nuclear charge number.The present dipole polarizabilities in Tables 5–8 can serve as the benchmark values for other prospective theoretical calculations.
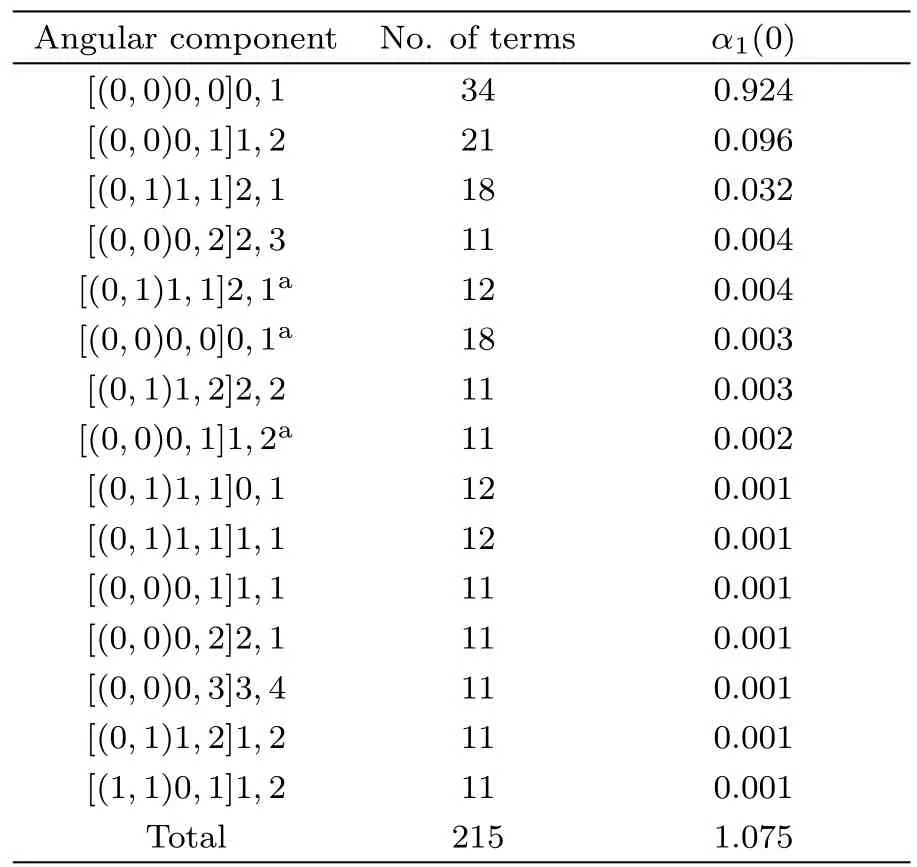
Table 6 The convergence pattern of the dipole polarizability α1(0)of the ground state for the the O4+ion.(in a.u.)
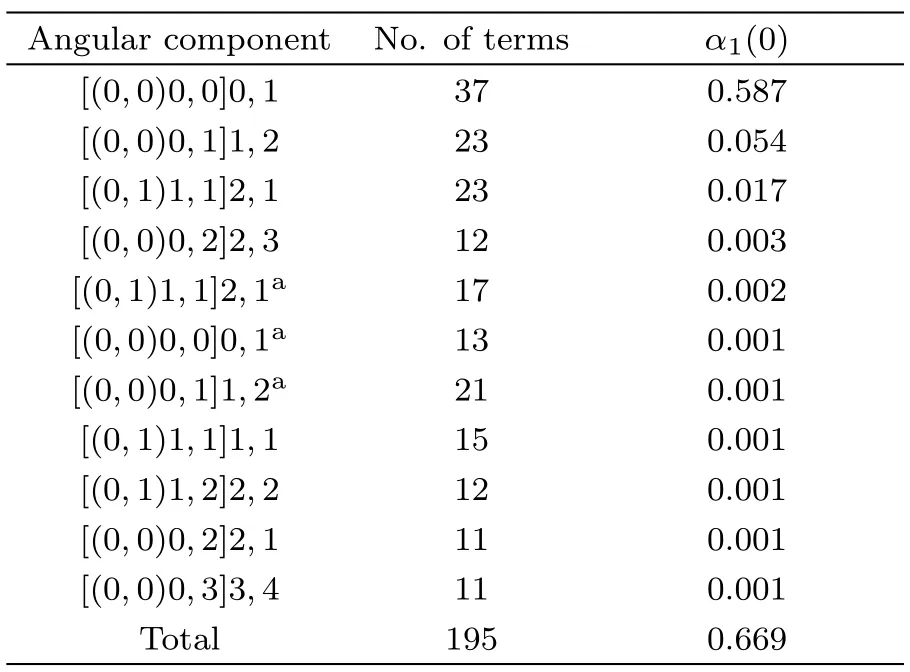
Table 7 The convergence pattern of the dipole polarizability α1(0)of the ground state for the the F5+ion.(in a.u.)
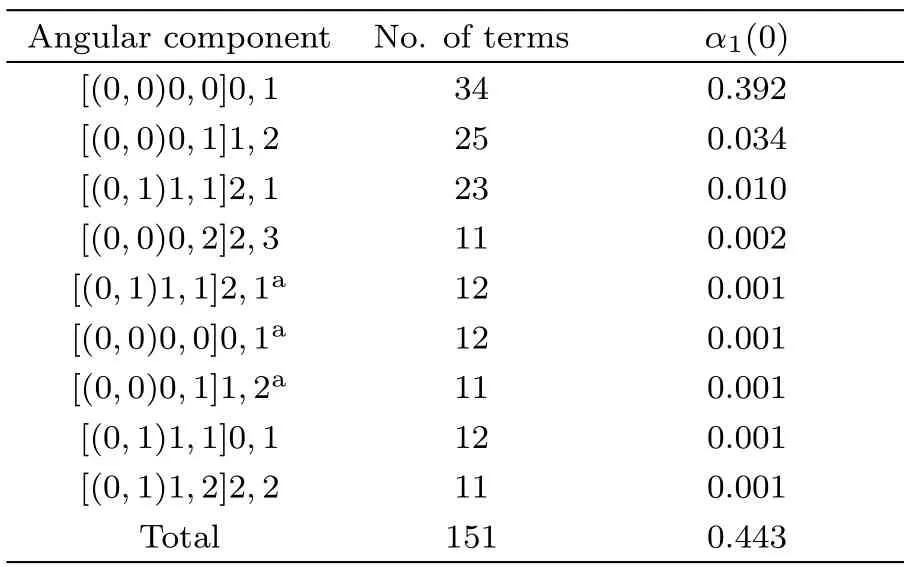
Table 8 The convergence pattern of the dipole polarizability α1(0)of the ground state for the the Ne6+ion.(in a.u.)
Dynamic dipole polarizabilities of the ground state for the beryllium atom are evaluated at monotonically increasing frequencies from zero value and compared with other theoretical values in the literature in Table 9.The present results are in perfect agreement with other elaborate theoretical values from exponentially correlated Gaussian functions[34−35]in whole.The present dynamic dipole polarizabilities agree with the values from these Hylleraas basis to four to five effective figures.To our knowledge,the reports on dynamic dipole polarizabilities of the ground states for berylliumlike systems with Z>4 are very scarce in the literature;therefore more studies are expected to appear in future,so that we can do follow-up studies.
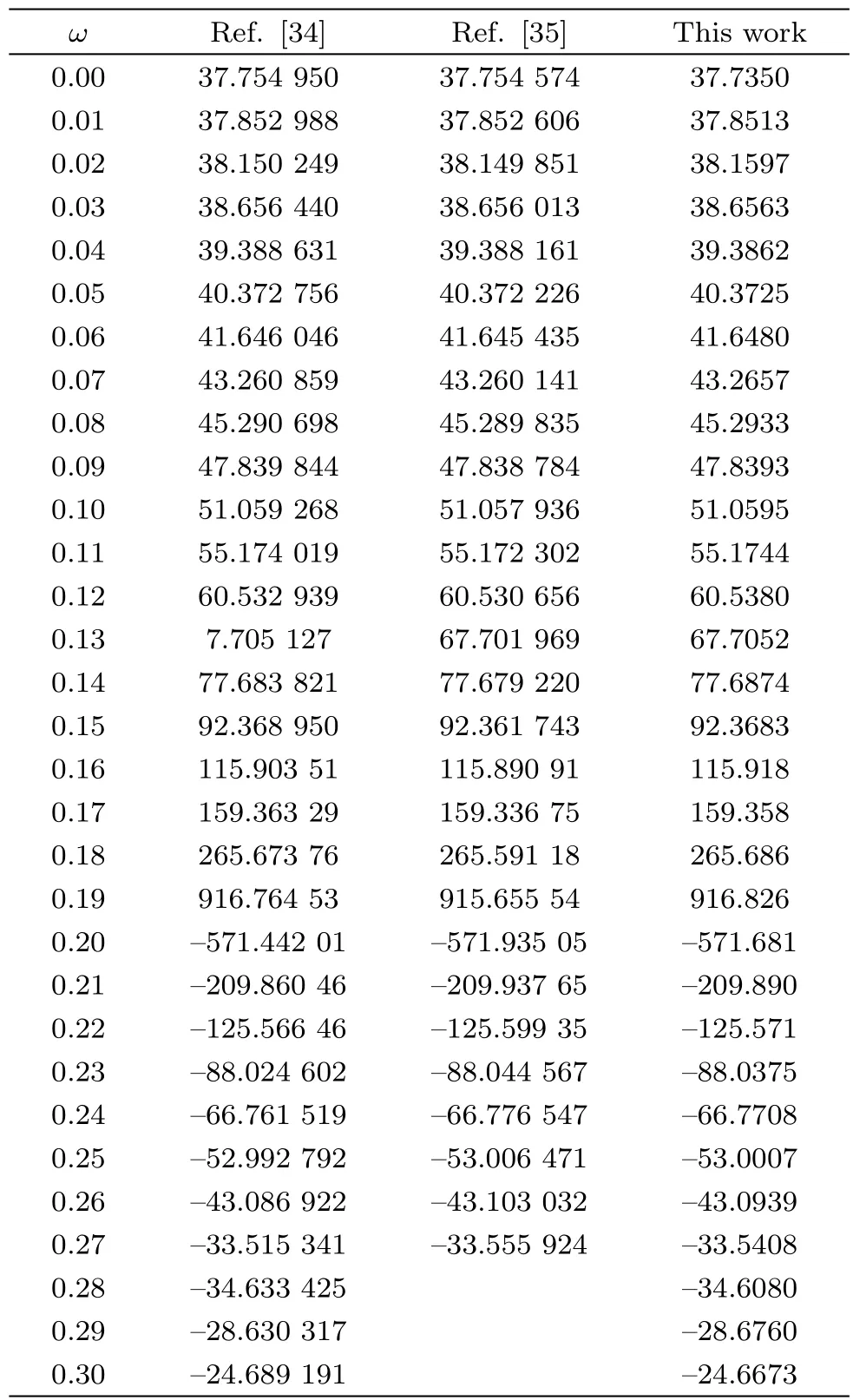
Table 9 Dynamic dipole polarizabilities α1(ω)of the ground state for the beryllium atom at selected frequencies ω obtained from different methods.(in a.u.)
4 Conclusions
In this work,the Rayleigh-Ritz variational method with multiconfiguration interaction wave functions are used to calculate the dipole polarizabilities of the ground states for berylliumlike systems with Z=4 to 10.The detailed convergence models of the dipole polarizabilities are studied.The most important contribution to dipole polarizabilities comes from the[(0,0)0,0]0,1 component.The present dipole polarizabilities are in good agreement with accurate theoretical values available in the literature.For berylliumlike systems with Z=7 to 10,there is no other report in the literature,so the present calculations may provide benchmark data for future studies.Dynamic dipole polarizabilities of the ground state for the beryllium atom at selected frequencies are also calculated.
 Communications in Theoretical Physics2018年12期
Communications in Theoretical Physics2018年12期
- Communications in Theoretical Physics的其它文章
- Mixed Local-Nonlocal Vector Schrödinger Equations and Their Breather Solutions∗
- Circular Semi-Quantum Secret Sharing Using Single Particles∗
- Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation∗
- Runaway Directions in O’Raifeartaigh Models∗
- The 1/NcExpansion in Hadron Effective Field Theory∗
- Quasinormal Modes of the Planar Black Holes of a Particular Lovelock Theory∗
