“美丽的”误会

（石河子第一中学 新疆石河子 832000）

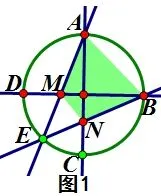
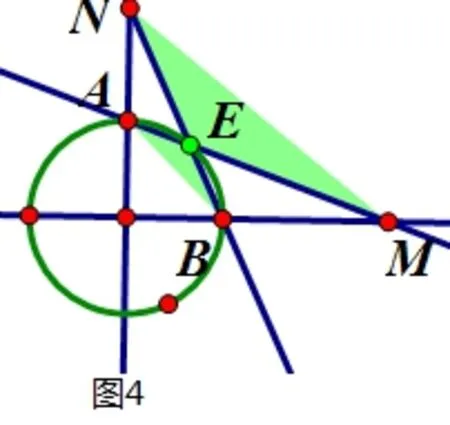
我就打开几何画板和学生一起做探索，让点E在弧CD上运动，同时度量四边形AMNB的面积，发现恒成立，随后我给出了下面的证明：

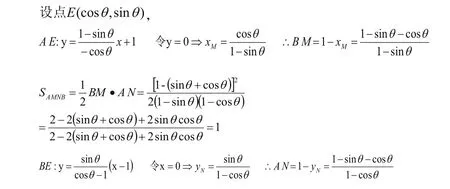
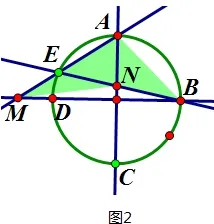
在我奋笔疾书时,学生兴奋的用鼠标拖动点E，意外发现不论点E在哪个象限，S总为定值，于是我就和学生对点E在第二、第三象限的情况进行探索（此时四边形AMNB均为凹四边形，如图2，图3），发现这两种情况同样符合关系式这样，之前的证法照样能用，正当我准备验证一下第一象限的情况时，上课的预备铃响了，我就简单的说了句：”第一象限时同样可证。”草草结束了讲解。

两节课结束后，意犹未尽的我又打开刚才的几何画板文件，拖动E到第一象限时发现四边形形状很奇特，不妨称之为“十字四边形”，此时四边形的面积好像不是我度量了发现这说明我刚才给学生讲错了，但为什么几何画板文件显示为常数呢？我马上在这个图中探索了的几何意义，

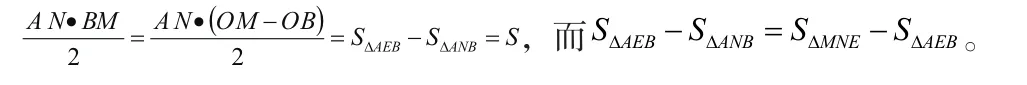
这样就解决了第一个困惑，但是另一个问题又来了：“十字四边形”的面积这样算合理吗？有没有一般情况下的四边形面积公式？

我百度了好一会儿，居然找不到以坐标形式呈现的任意四边形面积公式，只好自行探究：

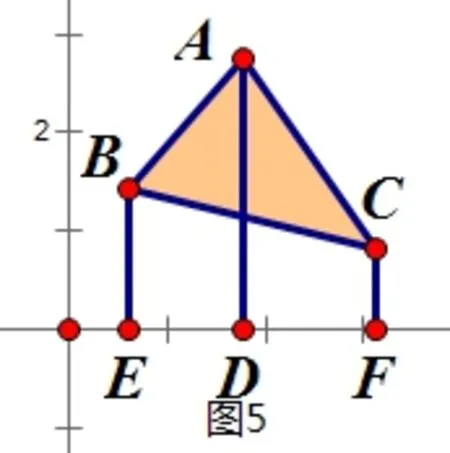
如图5：

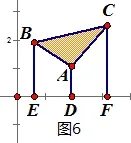
如图6：

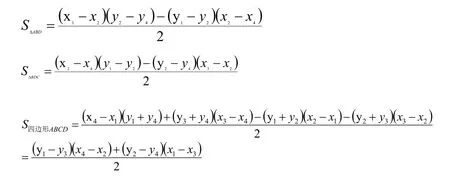
考虑到：凸四边形的两点若要具有对称轮换性，须满足：两个点的下标互换后不影响任何一边的图形位置，故只有对角线上两点具有对称轮换性，但此时上式中S四边形ABCD取相反数，故面积须加绝对值，

这应该就是几何画板软件默认的任意四边形面积公式。

3.下面检验凹四边形和“十字四边形”：

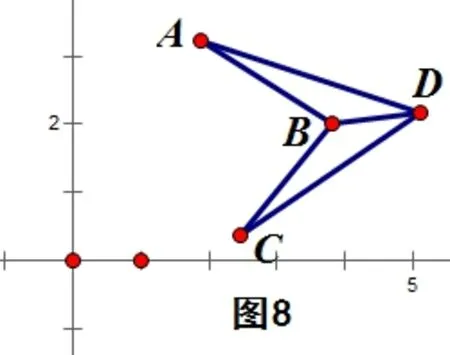
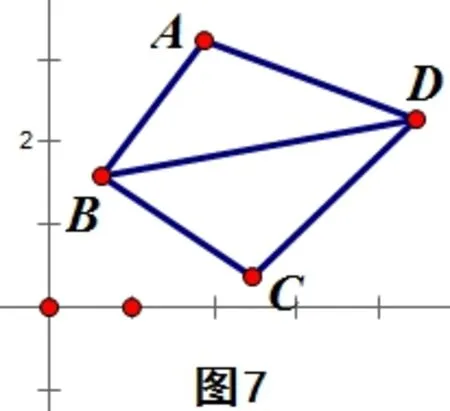
如图8中的凹四边形：引用图5和图6的公式

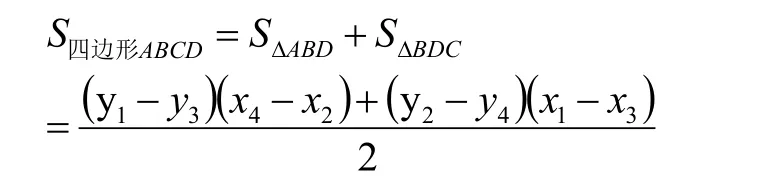
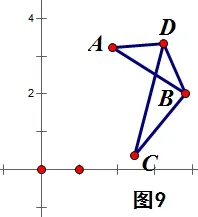
如图9中的“十字四边形”：引用图5和图6的公式

图8中的SΔABD和图9中的SΔABD同号，图8中的SΔBCD和图9中的SΔBCD异号，

套用之前的四边形面积公式此时将会得出：

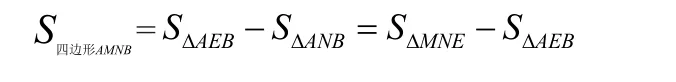
原来这才是之前出错的根源。而且我们顺带着得到一个结论：之前的面积公式适用于一般的凸四边形和凹四边形，但对“十字四边形”不适用。还有一个小小的遗憾，暂时没找到这个问题的纯平面几何证法。

最后，我要感谢来问题的学生，给了我一个这么好的研究素材；同时，我也庆幸：对于“十字四边形”多看了一会儿，才有了后续的这些发现。