一种改进的地铁车辆转向架轴承故障诊断方法
刘建强, 赵东明, 赵 楠
(北京交通大学 电气工程学院, 北京 100044)
随着城市轨道交通建设的快速发展,地铁车辆的正常、安全运行愈发重要。转向架轴承作为地铁车辆的重要部件,一旦出现故障,将会危及车辆的安全,甚至引发事故,快速、准确地诊断其故障状态对于地铁车辆的行车安全具有重大意义。
轴承发生局部故障时,振动信号的故障特征相对明显且易于监测[1]。基于振动信号的轴承故障诊断方法主要有时域分析法、频域分析法和时频分析法。由于轴承故障时,振动信号表现出非线性、非平稳性[2],时频分析法得到很多专家学者的认可。小波包变换是一种重要的时频分析工具,可以将信号既不交叠也不遗漏地分解到各个频带,提高时频分辨率,在轴承振动信号分析中具有重要的应用[3]。
转向架轴承发生故障时,故障特征极容易受到轮轨激扰和环境随机噪声的影响,尤其在轴承故障早期,甚至有可能被这些干扰所淹没,造成故障诊断效率降低甚至诊断失败。为了削弱激扰和随机噪声的影响,很多专家学者做出了研究。文献[4-5]利用EMD分解的滤波特性,将分解后的本征模态分量进行重组得到降噪后的信号,具有一定的降噪效果。但是,EMD分解存在端点效应和模态混叠等固有的缺陷。文献[6-8]研究了信号和噪声的奇异值属性,利用奇异值分解技术去除信号中的随机噪声。但是,奇异值分解降噪法中重构矩阵的行列数和阶次等的确定没有成熟普适的方法,而且其降噪效果也容易受这些参数的影响。
本文在研究了地铁车辆转向架轴承故障特征和干扰特性的基础之上,提出一种基于信号预处理和自适应小波包包络分析的轴承故障诊断方法。该方法首先利用巴特沃斯高通滤波器和S-G滤波器相结合,削弱信号中的激扰和随机噪声的影响。利用小波包分析工具将预处理后的信号等频分解为8个频带,基于峭度指标分析,自适应地调整各个频带的包络分析和故障搜索顺序,从而快速、准确地诊断轴承故障。为了验证提出的故障诊断方法的有效性,搭建了轴承故障实验平台。实验结果表明,经过预处理后的信号,故障特征更加明显,提出的故障诊断方法能快速、准确地诊断轴承故障。
1 信号预处理
转向架轴承由于其工作环境的特殊性,干扰噪声的成分和频率十分复杂,主要有列车运行中的轮轨激扰和环境随机噪声。对于轴承振动信号的预处理,需要对这两类干扰成分分别采取相应的措施。
列车运行中,轨道不平顺、轨道道岔、车轮缺陷等都引起轮轨激扰,该激扰混杂在轴承振动信号中。文献资料表明,车辆运行中各种轮轨激扰的频率成分一般低于1 kHz[9]。所以,采用巴特沃斯高通滤波器对激扰成分进行滤波处理。利用Matlab中的butter函数和filter函数实现巴特沃斯高通滤波器的功能,截止频率设定为1 kHz,对信号中的低频激扰进行预处理。
此外,列车运行中随机出现的干扰产生大量的随机噪声成分[10]。对于这种随机噪声,采用S-G滤波器进行预处理。S-G滤波器[11]是Savitzky和Golay提出的一种时域内的滤波方法,通过对待处理信号中宽度为M的窗口中的数据点进行阶次为n的最小二乘多项式拟合,将拟合得到的函数在数据窗口中心点处的取值代替原始数据作为其滤波值,然后向前移动窗口并重复拟合取值过程,直到所有的信号点拟合结束,可以达到对原信号进行滤波的作用。S-G滤波器的作用与带通滤波器相似,在通带频率范围内的信号可以完全通过,通带频率范围之外的信号会得到抑制或者急剧衰减,从而使有用信号和噪声信号得以分离。相比于普通的带通滤波器,S-G滤波器具有形式简单、设计方便的优点,并且不需要确定信号的截止频率就可以达到不错的降噪效果。其理论推导过程如下:设xi(i=-M,…,0,…,M)表示原始信号x在i点处的幅值,构造一个n阶多项式y拟合xi。设y在i点的表达式为
n≤2M
(1)
yi和xi之间的拟合误差为
(2)
为了使拟合误差最小,需要令e对yi的系数ar的偏导数为0,即
r=0,1,…,n
(3)
计算化简为
(4)
由于ak和i没有关联,所以
(5)
考虑到滤波的效果和计算量的均衡,一般取M=2,n=3。分别取r=0,1,…,n,对式(5)进行化简计算,可以得到a0,a1,a2,a3的表达式,将其带入yi的表达式中,可以得到yi的通用表达式。取i=±2,±1,0,得到y-2,y-1,y0,y1,y2。用y-2,y-1表示xi的起始2个点,用y1,y2表示xi的最后2个点,用一般化的y0表示xi中间的点。由此,我们得到S-G滤波器的表达式
(6)
式中:i=3,4,…,N-2,N为信号点数;y即为原始信号x滤波处理后的信号。
2 自适应小波包包络分析
2.1 小波包变换
小波变换是一种有效的时频分析工具[12],但是他只对信号的低频部分进行分解,导致信号高频部分的频率分辨率比较差。小波包变换在小波变换的基础之上,对高频部分也进行了分解,以3层小波包分解为例,原始信号S分解为低频频带A和高频频带D,再经过2层分解,形成8个不同频段的信号,见图1。
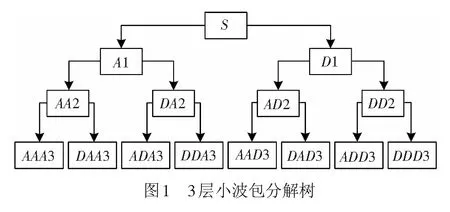
小波包分解算法[13]为
(7)
小波包重构算法为
(8)
式中:di,j,m为第j层第m个频带的第i个小波包分解系数。
2.2 基于峭度指标的自适应包络分析
2.2.1 自适应峭度准则
对于轴承振动信号,正常轴承振动信号的幅值基本满足正态分布,峭度指标接近3.0;一旦轴承出现诸如点蚀、局部剥落等故障,那么振动信号中会出现大量周期性冲击脉冲,并且这种冲击脉冲的幅值往往比较大,使得信号幅值的分布偏离正态分布,从而导致峭度指标大于3.0。故障越严重,振动信号的幅值越偏离正态分布,相应的峭度指标数值就越大。因此,信号峭度指标的大小在很大程度上能反映该信号含有故障特征可能性的大小。其计算式为
(9)
式中:xrms为信号xi的方均根值;N为信号点数。从峭度指标的定义可知,其分子是信号的4次方,分母是方均根值的4次方,故障轴承振动信号中的冲击成分会引起分子的急剧增大,而分母的增大相对较小,从而引起峭度指标值发生显著的变化,因而峭度指标对轴承故障冲击非常敏感。
通过对小波包变换后每个频带峭度指标的分析,可自适应地决定各频带的包络分析顺序以及是否需要继续对某些频带信号进行包络分析。
2.2.2Hilbert变换

(10)
式中:τ为积分变量。式(10)表示对原始信号g(t)求取卷积积分,也可表达为
(11)

(12)
表示成复数形式为
g+(t)=A(t)ejφ(t)
(13)
式中:模值A(t)为g(t)的包络。
(14)
为了得到信号的包络谱,需要利用快速傅里叶变换工具对包络A(t)进行进一步处理,进而从中提取故障信息。
3 基于信号预处理和自适应小波包包络分析的轴承故障诊断方法
当车辆转向架轴承发生故障时,故障点周期性地接触轴承其他部分,将激起轴承系统的固有振动,同时上述振动也受到轴承故障特征频率的调制。通过包络谱分析可以提取故障特征。但是由于转向架轴承运行工况的特殊性,轴承振动信号往往受到轮轨激扰和环境随机噪声的影响,所以要通过相应的预处理方法削弱振动信号中的干扰成分。文献[15]提出了一种轴承故障诊断方法,利用3层小波包分解、重构将信号分解成8个频带,然后依次对每个频带进行包络谱分析,使用提出的搜索算法诊断轴承故障。这样的诊断方法过于盲目,并且非常浪费时间。
为了缩短故障诊断的时间,提高诊断效率,经过理论分析和大量实验,本文提出了自适应小波包包络分析诊断方法。由于故障轴承振动信号的峭度指标比较大,所以预先对小波包变换后的8个频带进行峭度指标分析,按照各频带峭度指标的大小,自适应的决定进行包络谱分析和故障识别的频带顺序,即峭度指标大的频带优先分析,峭度指标小的频带延后分析。当在某频带中搜索到故障,则不再进行其后各频带的包络谱分析。这样一方面提高了诊断效率,另一方面也不会丢失任何故障信息。
基于以上论述,该方法的步骤为
Step1首先对采集的轴承振动信号进行信号预处理。即利用巴特沃斯高通滤波器滤除低频激扰成分,利用S-G滤波器削弱随机噪声成分。
Step2对预处理后的信号利用db4小波进行3层小波包分解和重构,将信号分解到8个频带。
Step3求取各频带峭度指标,并对峭度指标从大到小进行排序。
Step4按照Step3中的排序,利用Hilbert变换和FFT依次求取相应频带的包络谱并利用搜索算法搜索包络谱图。若搜索到故障特征,则结束本次故障诊断,输出诊断结果;若未搜索到故障特征,则按顺序分析下一频带。
4 实验研究
4.1 轴承故障诊断实验平台
为了验证所提出方法的正确性,构建了轴承故障诊断测试台,见图2。实验平台中,使用额定功率为2.2 kW、额定转速为1 410 r/min的西门子1LG0106-4AA20型电机拖动轴承运转。使用液压千斤顶加压模拟负载,使用振动传感器(HK8100)采集轴承振动加速度信号,并以电压信号的形式输出到信号采集单元进而存储在计算机中,利用Matlab软件完成采集数据的处理分析。

4.2 实验验证
使用广州地铁公司提供的有局部故障的轴承进行实验。轴承具体参数为型号为BC1B326441A/HB1(SKF公司),类型为圆柱滚子轴承,轴承节径D为176 mm, 滚动体直径d为26 mm,滚动体数目z为18,接触角α为0°。
压力设置为9.8 kN,电机转速控制为540 r/min(即电机输出频率fr=9 Hz)。运行一段时间并采集振动信号。滚动轴承存在局部缺陷故障时,内圈故障特征频率为
(15)
外圈故障特征频率为
(16)
滚动体故障特征频率为
(17)
由式(15)~式(17)可得,该实验条件下,内圈、外圈、滚动体故障特征频率分别为92.97、69.03、29.796 Hz。
使用内圈存在故障的轴承验证本文提出的诊断方法的有效性。首先将采集的振动信号(32 768点)利用Matlab进行加噪处理,即利用正弦函数产生频率为500 Hz、幅值为0.2 V的离散信号模拟低频激扰,利用awgn函数向原始振动信号添加随机白噪声。带噪信号的时域波形和包络谱局部波形,见图3。

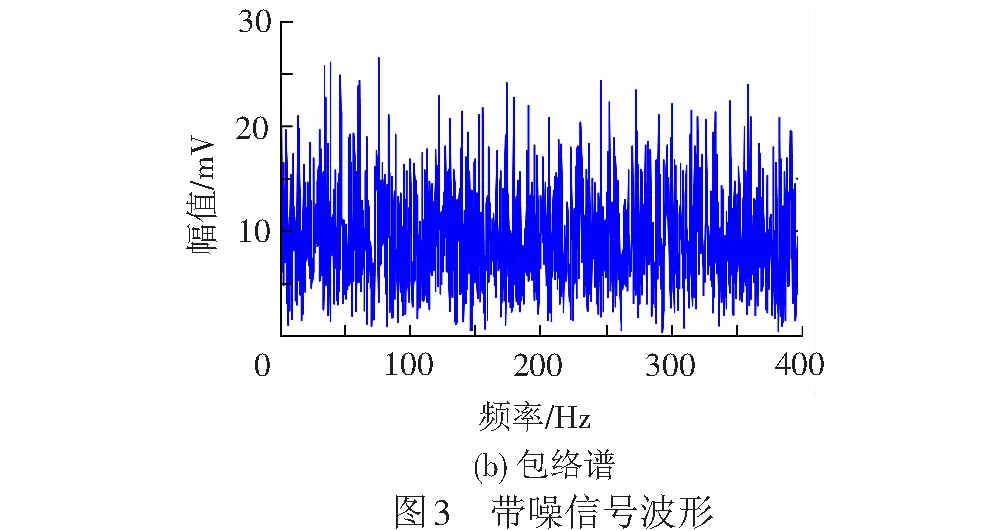
由图3可见,由于受到激扰和随机噪声的干扰,轴承振动信号的时域波形和包络谱波形中,都没有发现明显的故障特征,导致诊断失败。
利用本文提出的故障诊断方法进行故障诊断。首先对原始振动信号进行降噪预处理,经过预处理后振动信号的时域波形见图4。
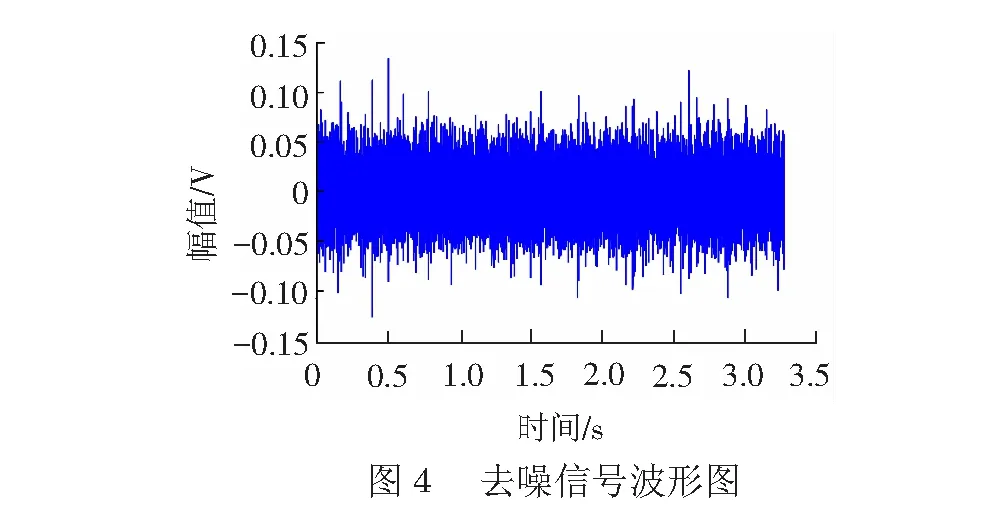
从去噪信号波形中可以看到,激扰和随机噪声成分已经得到削弱,振动信号中存在较明显的冲击,轴承可能存在故障。

利用db4小波对预处理后的信号进行3层小波包分解,重构后8个频带的时域波形见图5。
对重构后每个频带的信号进行峭度指标分析,各个频带的峭度指标大小见表1。根据峭度指标的大小自适应决定各个频带的分析顺序。基于Matlab平台,采用m语言编写故障诊断算法,输出结果为U=1,f=93.073 6 Hz,i=1,pos=8。

表1 各频带峭度指标

输出结果U=1,f=93.073 6 Hz表明在93.073 6 Hz处存在明显的谱峰(该频率处于内圈故障特征频率的可接受误差范围内),诊断为轴承存在内圈故障,与实际情况一致,此外,pos=8说明诊断结果是在小波包分解重构后按照自然排序的第8个频带信号中得到的,而i=1说明通过峭度指标分析,该频带的峭度指标最大,所以算法自适应地将该频带调整为第一个进行包络分析处理,从而快速地诊断出了轴承故障。8个频带的包络谱波形见图6,诊断出故障的频带包络谱波形的局部放大图见图7。包络谱图中显示内圈故障特征频率处的确出现了明显的峰值,说明本文所提出方法是正确的。实际上,当程序自适应地调整各个频带的分析顺序并在调整顺序后第一个频带中诊断出了故障,将不会继续分析其他频带,从而进一步节省诊断时间和资源。
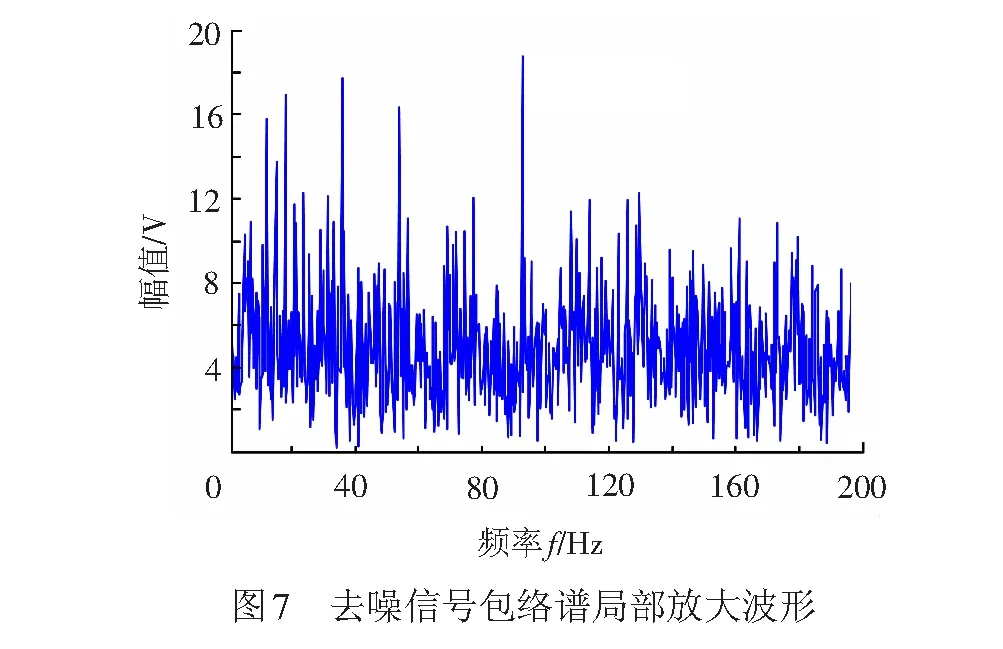
如果使用文献[15]中的诊断方法,直接按照小波包分解重构后各个频带的自然顺序依次进行包络分析和故障搜索,发现程序需要花费对前7个频带进行包络分析和故障搜索的时间,才可以在第8个频带搜索到故障。而本文提出的方法可以利用峭度指标自适应调整频带分析顺序,调整后在第一个频带即可诊断出故障。相比之下,本文提出的方法效率更高。
此外,通过轴承测试台对具有滚动体、外圈故障的轴承检测表明,本文所提出的方法同样快速准确地诊断出了故障,进一步验证了本文所提出方法的快速性和正确性。
实际应用中,可在车辆转向架轴箱上安装振动加速度传感器,振动加速度信号输出给信号采集单元。采集单元采用本文所提出诊断方法,实现实时在线分析轴承的故障状态,一旦诊断出故障,通过故障标志变量的值驱动报警装置进行报警,可在列车运行条件下快速、准确地对转向架轴承进行实时故障诊断。
5 结束语
转向架轴承部件的正常运转对于地铁列车的安全运行具有重大意义。为了对其故障状态进行快速、准确地诊断,本文提出了一种基于信号预处理和自适应小波包包络分析的转向架轴承故障诊断方法。该方法首先对采集的振动信号进行降噪预处理,以削弱信号中的激扰和随机噪声成分,在此基础上进行自适应小波包包络分析,快速提取轴承的故障特征并作出诊断。为了验证所提出故障诊断方法的正确性,搭建轴承测试台并开展实验研究。实验结果表明,该方法能够在无人参与的情况下准确、快速地实现轴承故障诊断,是一种符合实际需求的故障诊断方法。

