基于旅行费用约束的景点及路径动态规划研究

方苏杰 张宇航 方成刚

1(南京师范大学附属中学 江苏 南京 210003)2(南京工业大学 江苏 南京 211800)

0 引 言

随着生活水平的提高，人们对旅游消费的热情一直处于持续增长的过程。游览景点的规划是否合理对于旅行过程的感受至关重要，合理的游览路径不仅使旅行者感到时间安排合理、费用合算、旅游感观价值高，还能使旅行社降低成本、提高效益、提升好评指数。游览景点规划问题从不同角度对旅行过程进行优化，如从最短时间、最小费用、最短距离等不同方面对旅游景点进行寻优[1-3]。文献[4]以庐山为例，以一日游为时间约束，利用Dijkstra算法实现尽可能多景点的最短路径规划；文献[5]以旅游成本和游客舒适度为目标函数，利用遗传算法对全国201个5A级景区的旅游路径进行优化。

传统的游览景点规划通常以成本最小作为优化目标，但对于旅行社或旅行者常常需要针对一定的旅行预算费用进行规划，并希望在预算费用范围内尽可能游览更多综合性价比高的景点。

1 问题描述与分析

旅行费用通常包括交通费、住宿膳食费、门票费等几个部分，不同的游览景点规划将导致上述几个费用比例发生变化。对于旅行社或旅行者而言，如何优化选择旅游景点以便在合理的预算费用范围内游览更多评价指数高的景点是一个经常遇见的问题。

该问题难点在于旅行总费用随景点规划的不确定而发生动态变化，需要通过优化算法在预算费用范围内选择合适的游览景点以降低交通食宿费所占比例，增强旅行体验。上述问题求解可归结为两个方面：① 在预算费用约束条件下挑选尽可能多的高综合评价指数景点，即0-1背包问题。② 遍历规划景点最短路径以降低交通食宿费比例，即旅行商问题。

本文利用二分法及动态规划算法，并结合上述两个经典问题对基于旅行预算费用约束的游览景点进行规划，以获取最大旅行价值体验。此方法不仅适用于游览景点规划，亦可用于管路铺设、道路修建等路径规划问题。

2 数学建模及动态规划求解

为简化起见，对上述旅游景点规划问题做以下几点假设：

(1) 旅行总费用T总为：

T总=T景点+T交通+T食宿

式中：T景点为旅行景点产生的费用，本例仅考虑门票费用总和；T交通为遍历各个规划旅游景点的交通费用总和；T食宿为旅行食宿费用总和，本例景点旅行时间每增加8个小时，则旅行天数增加一天。

(2) 采用自驾出行，交通费及交通时间与距离成线性关系。

(3) 交通与游览时间之和每大于10小时，需要增加一次住宿膳食费。

2.1 景点综合评价指数建模

景点主要参考指标及综合评价指数如表1所示。

表1 景点主要参考指标及综合评价指数

设影响每个景点综合评价指数的主要因素包括以下几个方面：

n1——质量等级，按《旅游景区质量等级的划分与评定》(GB/T 17775-2003)对景区的综合评分，分为A、AA、AAA、AAAA、AAAAA五个等级；

a1——游客评价，通过网评方式由游客对景区进行游览体验评价，其评价指数可采用5分制；

ci——景区门票费用；

ti——景区平均游览时间；

对上述参考指标进行归一化处理，并通过相关指标对景区进行综合评价，其评价函数pi为:

(1)

式中：ω1为质量等级权重，质量等级指标由政府机构进行评估，可信度高，其权重取值可相对较大；ω2为游客评价权重；ω3为游览时间/游览费用权重。对于费用为零的景点，取ti/ci=1。

2.2 基于预算费用约束的游览景点规划[6-7]

如表1中共有n个景点，第i个景点的游览费用为ci，综合评价指数为pi，则在满足游览预算费用C的条件下选择合适的景点，并使其综合评价指数之和最大，其数学模型如下：

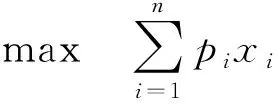
(2)

式中：xi=1，表示该景点被选中；xi=0，表示该景点未被选中。

上述数学模型是一个整数规划问题，可采用递归算法进行求解。假设已经完成景点1，2，…，i-1的规划，剩余游览费用为j，则对i，i+1，…，n个景点进行规划的最优解m(i，j)为：

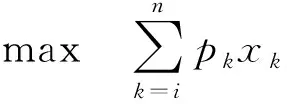
(3)

建立m(i，j)的递归计算式为：

(4)

2.3 遍历景点最短路径规划[8-9]

通过上述算法在n个景点中选择了m个景点，进一步规划遍历m个景点的最短路径以降低交通食宿费的比例。设景点的集合为V，为第i个景点到第j个景点之间的距离，则遍历各旅游景点最短路径的数学模型如下：

(5)

由于遍历最短路径与出发点无关，故可从任一景点i开始进行路径寻优。令d(i,V′)为从景点i出发经过V′(寻优初始时，V′=V-{i})中各个景点一次且仅一次，最后回到出发点i的最短路径长度。则求解d(i,V′)的动态规划函数为：

d(i,V′)=min{cik+d(k,V′-{k})} (k∈V′)

(6)

d(k,{})=cki(k≠i)

2.4 基于二分法的循环优化

理想的景点规划结果应提高游览费用在总费用中的比例，尽可能游览更多综合评价指数高的景点。但在景点规划的开始阶段并不确定旅游费用中各个组成部分的比例，因此在利用式(2)进行景点规划时，需要初定游览费用比例，根据此设定费用进行景点规划。本文采用二分法先初定游览费用在总费用中的比例，再利用0-1背包算法挑选出合适的景点；进一步利用式(5)的旅行商算法遍历前述规划景点最短路径，计算出相应的交通食宿费；最后验算规划费用与预算费用的差值绝对值是否小于允差，如不符合则使用二分法调整游览费用比例继续进行优化，直至符合条件为止。上述算法流程图如图1所示。

图1 景点规划流程图

2.5 算法时间复杂性分析

上述算法包括三个部分，其时间复杂度如下：

1) 基于二分法的费用区间搜索，时间复杂度为O(log(n))；

2) 基于动态规划法的0-1背包求解，时间复杂度为O(n×C)；

3) 基于动态规划法的旅行商(TSP)求解，时间复杂度为O(n2×2n)。

按照上述算法循环规则计算整个程序的时间复杂度为O(max(log(n)×(n×C)，log(n)×(n2×2n))。由算法复杂度与时间效率关系可知该算法的效率较高，适用于旅游景点规划一类计算量相对较小的场合，且可以获得全局最优解。

3 算例分析

南京是中国十大风景名胜之一，其年度旅游总收入亦在国内排名前列，南京拥有钟山风景区、夫子庙、总统府、秦淮河、玄武湖等优质旅游资源[10-11]。本文以南京的主要旅游景点为例(见表2)，景点的距离矩阵见表3，通过上述算法在规定预算费用范围内进行景点优化选择。

表2 南京主要景点的相关指标列表

表3 景点间距离矩阵

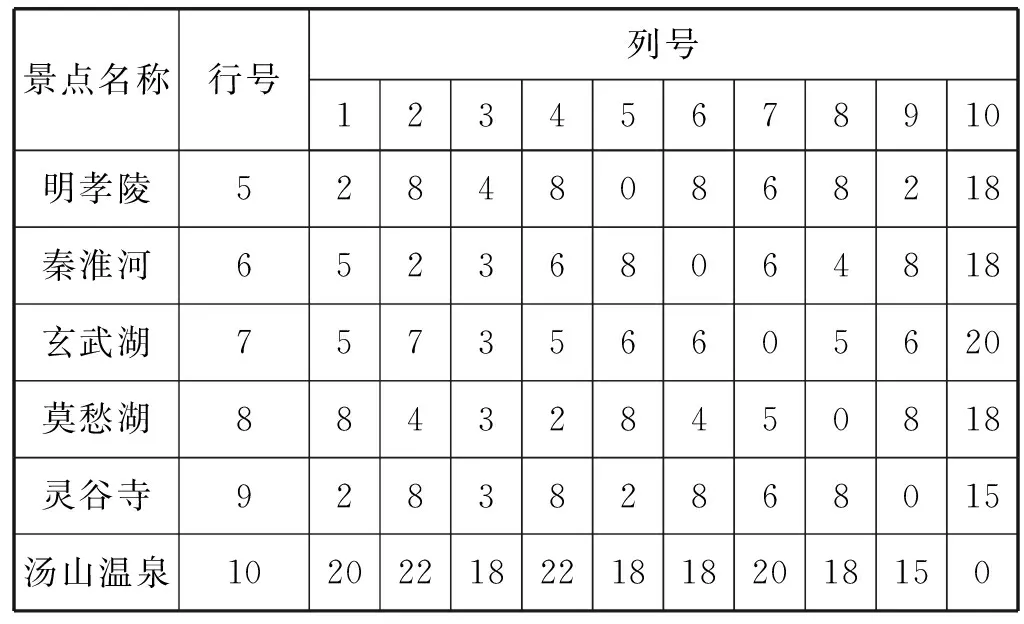
续表3

假设旅行食宿费为400元/天，交通费为3元/公里。利用MATLAB进行编程分别对旅行预算总费用为1 000元和500元两种情况进行规划，其计算结果见表4及图2、图3。

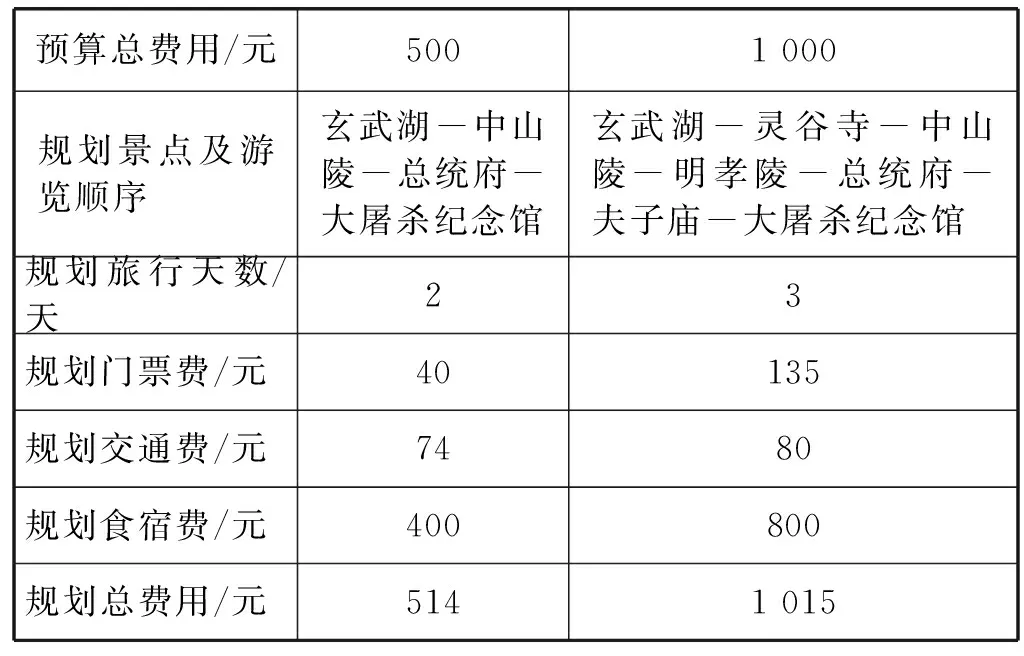
表4 按不同预算费用的规划结果比较

图3 预算总费用1 000元规划结果

将上述算法利用java开发成基于安卓系统运行的APP，其界面如图4、图5所示，用户仅需要输入城市和旅行费用预算等相关参数，即可得到规划结果，如图6所示。

图4 城市选择界面

图5 参数输入界面

图6 规划结果界面

4 结 语

本文提出了以总旅行预算费用为约束条件获取最大旅行体验的旅游景点规划问题，建立了景点综合评价指数模型。通过0-1背包算法求得费用约束条件下综合评价指数最高的景点集合，再利用旅行商算法遍历景点获取最短游览路径以降低交通费用，最后通过二分法循环优化上述过程得到景点规划最优解。

本文以南京主要景点为例给出其景点评价指数和景点距离矩阵，通过上述优化算法分别对预算总费用为1 000元和500元两种情况进行规划，其规划景点及游览路径合理，满足预算费用要求。