基于分段线性坐标优化的退化压缩感知水印检测
陈 晓 锋
(浙江大学宁波理工学院信息科学与工程学院 浙江 宁波 315000)
0 引 言
在无线移动信道(开放信道)上的多媒体数据传输面临诸如版权保护和有限传输带宽等安全问题。数字水印一般是隐含着著作权者的相关信息,用于版权归属设定,用户对数据信息的处理需要首先对水印代码进行处理。数字水印具有两种属性:永久嵌入属性和易于读取属性,同时不能被人体视觉轻易感知到,并且嵌入的水印与原始信息之间不存在较为明显的干扰。为了安全起见,嵌入水印不可被用户轻易地删除。虽然水印需要进行永久性标识,但相对而言不可对原始数据信息的访问产生影响[1-2]。
当前的数字水印研究中已有很多成熟的算法。例如文献[3]将图像中常用的数字水印算法拓展到音视频等多种格式数据文件中,采用的基本方式是利用扩频方式进行数字水印的显频分量隐藏,问题是算法简单的进行移植操作,其算法适应性相对较差。文献[4]采用傅里叶算法对版权图像的数字水印问题进行研究,将数字水印按照非递增序列的形式进行嵌入,缺点是算法存在较大的失真问题,水印与原始图像之间存在较大的干扰问题。文献[5]采用图像融合方式进行数字水印的嵌入,其可有效防止用户的随意复制,缺点是水印的嵌入分辨率较差。文献[6]采用小波算法对数字水印问题进行研究,提出了具有可变换分辨率算法的数字水印检测方法,缺点是算法的计算复杂度过高。文献[7]设计了一种具有互补特性的数字水印检测方法,算法的优点是不需要对图像的原始数据信息进行参照,缺点是算法的水印检测精度偏低。文献[8]基于离散余弦变变换对数字水印算法的频域检测方案进行设计,可实现对水印图像的信息进行调制,对于水印的鲁棒攻击性具有较强的抵抗能力。
上述算法在进行数字水印算法进行设计过程中虽然针对某一方面进行了针对性的设计,但是其优化解具有局限性,是一种局部极优的数字水印检测方法。本文针对数字水印检测算法设计了一种最优化计算模型,是一种多准则极值优化问题。近些年,在多准则极值优化问题研究中,已有很多成熟的计算方法,例如权值法、灰度值法、熵值法、均衡法等。这些方法对于多准则极值问题,具有一定的优化效果,但是问题是算法的主观性过强,特别是算法的收敛性在理论上缺乏足够的收敛依据。对此,本文利用分段线性坐标优化算法对多极值目标优化问题进行研究,实现对数字水印检测的最优化实现。
从上述研究成果可知,以往的数字水印研究成果侧重的是算法的实现,对于主机信号干扰HSI和衰减退化影响检测器性能,考虑不是非常细致。为解决该问题,本文采用扩频SS水印和压缩感知CS进行算法融合,提出了一种优化问题模型,以最小化失真(包括CS重建和水印检测)作为优化指标,采用检测概率为特征的检测可靠性约束,进行最优测量次数(提供带宽)和嵌入强度的优化。
1 基于退化压缩感知的扩频水印检测
在原始变换空间Ψ∈RN×N中,将长度为N的具有零均值和单位方差的独立同分布(i.i.d)高斯模式P(∈RN)加到主机数据X∈RN×N中,如傅里叶、小波变换(这里使用)、离散余弦变换(DCT)等。SS水印可表示为:

(1)


图1 CS-SS水印图像传输和水印检测的系统模型
在检测器侧接收的CS测量y可表示为:

(2)

式(2)中的水印检测可以被建模为两个假设过程,H0(水印缺失)和H1(水印存在),如式(3)所示,均服从高斯分布。
(3)
式中:总干扰协方差矩阵是C可表示为:
C=E[yyH/H0]=E[(hφx+η)(hφx+η)H]=
(4)
式中:E(<φx,η>)=E(<η,φx>)=0;操作符〈p,q〉表示向量p和q的内积。基于φφH=IM,总干扰协方差矩阵C可改写为:
(5)
基于式(5),在H0和H1情况下,y的概率密度函数(PDF)可表示为:
(6)
式中:det(·)表示矩阵的行列式。测试统计量t(y)可推导为:
(7)

(8)
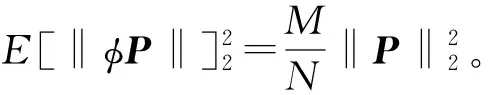

(9)
(10)
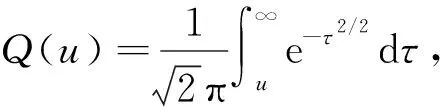
(11)
式中:对于已知的信道条件(退化函数)和给定的pfa,pd值取决于CS测量m的数目和水印强度α,即:
(12)
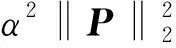

2 水印检测可靠性优化
由于CS和水印检测过程所导致的失真现象,可表示为如下模型:

(13)
计算失真(e)的平均“L2”范数,具体计算过程如下:
(14)

(15)

(16)
理论上,具有检测可靠性约束的优化框架可以表述为:
(17)
(18)
(19)
式中:d2=z+α2+M2。将约束优化问题转化为无约束优化问题,形式为:
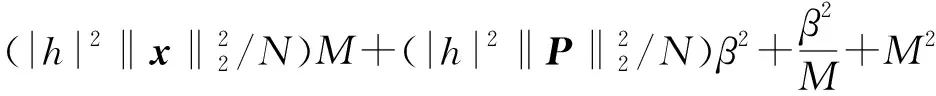
(20)
当▽d2|M=0时,可得到d2的最小值,即d2的梯度。因此,可得:

(21)
求解三次方程并放弃虚根,得到最优值M*的取值形式为:
M*= (b/2+((-a3/27+b/2)2-a6/729)1/2-
a3/27)1/3-a/3+a2/(9×(b/2+((b/2-
a3/27)2-a6/729)1/2-a3/27)1/3)
(22)

(23)
由此可得到目标函数(d2)的二阶导数,计算形式如下:
(24)
式中:▽2d2|M是正的,这清楚地表明目标函数的值是最优M*值的最小值。因此,在给定的pfa=ξ中,pd的最佳值可以通过在式(13)中代入α*和M*来获得。
3 分段线性坐标优化求解
3.1 算法描述
式(19)退化压缩感知的扩频水印检测模型的求解,可采用坐标法进行优化。一般来说,对于给定的水印检测模型网格顶点,主顶点位置上的扩频水印检测模型的值是最大的,而位于网汇聚点位置上的点最小,算法计算过程为:
Step1算法参数进行初始操作,设定t=1、k=1、i=1。
Step2设定分段线性坐标优化顶点νt=(i1,i2,i3),式中i1∪i2∪i3={1,2,3},参数i是分段线性坐标的图标号。
Step3查找xs=i,xs-1=max{Ns/xs},xs-2=max{Ns/(xs,xs-1)},…,x4=max{Ns/(xs,…,x5)}。采取升序方式对{Ns/(xs,xs-1…,x4)}进行序列的排列,且有j1 Step4查找xs=i,xs-1=min{Ns/xs},xs-2=min{Ns/(xs,xs-1)},…,x4=min{Ns/(xs,…,x5)}。采取升序方式对{Ns/(xs,xs-1,…,x4)}进行序列的排列,且有j1 Step5对于构建的坐标优化网络,对f(p1)和f(pst1)进行对比,可对算法下一步的搜索方向进行确定,对于设定参数y*,若满足f(p1)-y*≤y*-f(p1),按照从Sink节点到主顶点的逆向顺序进行数字水印检测模型的优化,并执行Step 6。若不满足,则采取相反的方向进行算法目标函数的搜索优化,并执行Step 7。该算法过程的优点是算法的执行效率较高。 Step6采取降序方式对目标输入xk排序,式中k∈Nk,jk>jk-1>…>j1。针对设定的序列jk⟺jk-1⟺…⟺j1进行坐标xk转换,将产生k-1个坐标p2,p3,…,pk,得到算法的上层代码,然后跳转到Step 8。 Step7采取升序方式对xk排序,k∈Nk,jk>jk-1>…>j1。针对设定的序列jk⟺jk-1⟺…⟺j1进行坐标xk转换,将产生k-1个坐标pst2,pst3,…,pstk,进而可得到算法的下层代码。 Step8基于求解的坐标,形式如下:对于优化目标f(pn)=f(pn-1)-Δn-1,根据函数取值进行排列,式中μ(λ)为码pn-1中jλ位置,Δn-1=(jn-jn-1)(cn-cμ(n-1))。 Step9按照顺序对下列条件进行检测: (a) 若满足水印检测模型条件f(pm)≥y*,则跳转Step 10,继续目标算法优化。 (b) 若满足水印检测模型条件f(pm) (c) 若满足水印检测模型条件f(pm) (d) 若满足t+1≤6,则转Step 2;否则,满足该约束下对算法进行终结。 Step10假定k=k+1,若满足k Step11采取降序方式对xk排序,k∈Nk,jk>jk-1>…>j1。针对设定的序列jk⟺jk-1⟺…⟺j1进行坐标xk转换,可产生k-1个坐标q2,q3,…,qk。 Step12基于坐标f(qn)=f(qn-1)-δn-1,δn-1=(jn-jn-1)(cn-cμ(n-1)),对函数排列值进行查找,μ(λ)是函数目标排列码qn-1中jλ所处的位置区域。 Step13若满足水印检测模型条件f(qn)≤y*,则保留坐标顶点qn,跳转Step 10。 对于多准则极值优化问题,对分段线性坐标优化求解算法进行设计: Step1对于目标模型输入,设定其参数约束以及目标准则。 Step2生成水印检测模型的组合元素。 Step3对于设定的约束k,基于改进坐标法对组合问题排列进行求解,可得到可行解集D*子集Di⊂X,i∈Nk。 Step4查找可行解D*=D1∩D2∩…∩Dk。 Step7对于点x∈D*位置进行函数f*值优化求解。 Step8对选取优化方向与Step 7所得数值进行对比,可得目标极值。 Step9对数字水印检测模型的线性分式函数近求解。终结算法。 数字水印检测模型的线性分式函数求解算法如图2所示。 图2 算法流程图 实验平台:CPU i7-6500k 2.9 GHz,RAM 6 GB DDR4 2 400 MHz,系统为Win10旗舰,仿真软件是MATLAB 2013b。选择lena(莱娜)测试图作为载体,Punjabi Logo作为水印,大小是M/3×N/3,图像大小M×N=300×300。 这里设定的最佳参数主要是M*和α。利用Daubechies 9/7小波对256×256,8位/像素莱娜图像(图3(a))进行小波变换,将其分解为3级。假定小波系数的分布遵循GSM模型。水印检测在方差小于阈值(1 000)的小波系数集合中。图3(b)和图3(c)分别给出用于78%的CS测量的水印图像(PSNR=44.86 dB)和重建水印图像(PSNR=32.96 dB)。利用CS测量的最佳值(M*=3 204),水印检测强度(α*=1.5),可获得具有零均值和方差0.7(h~CN(0,0.7))的复正态分布的瑞利衰落的水印检测强度,而具有零均值和方差0.25的加性高斯噪声(η~N(0,0.25))。 (a) 原始图像 (b) 水印图像 (c) 重构图像图3 实验图像 最佳参数M*和α的选取结果如图4所示。 (a) 最优CS测量中的归一化平均误差与水印检测强度(M*=3 204) (b) 归一化平均误差与CS测量在最佳水印检测 强度上的比较(α*=1.5)图4 测量结果对比 图5 检测概率对比 根据图5结果可知,文献[6]中的工作提出了一种鲁棒的和分层的CS水印方案,其中水印的检测可以在加密域或解密域中完成。本文算法相对于文献[6]算法可实现显著性能改进,约提升5.43%,因为本文采用的是最优检测器设计。 为了验证所提出的算法对于数字水印检测过程中高频分量影响的鲁棒性,利用噪声点对数字水印的嵌入过程进行模拟攻击测试。选取的模拟攻击噪声主要有4种类型,分别是:斑点、椒盐、压缩和滤波等。其中:斑点噪声的参数设置是mean=0,var=0.4;椒盐噪声的参数设置是var=0.4;压缩攻击过程的参数设置是Q=20;滤波攻击过程的参数设置是[50,50]。对比算法选取FrWT和FrDCT两种算法,分别见参考文献[14-15]。实验结果如图6所示。 (a) 斑点攻击 (b) 椒盐攻击 (c) 压缩攻击 (d) 滤波攻击图6 水印检测算法性能对比 根据图6的实验结果可知,当采用lena图像作为水印图像时,图6(a)、(b)以及(d)所示的椒盐攻击、斑点攻击、滤波攻击中,其类似于真实环境下的人造边缘攻击,是一种高频的攻击形式。实验结果显示,本文算法相对于文献[14-15]可得到更加清晰的数字水印图像,而文献[14-15]两种算法检测到水印图像存在非常明显的高频干扰,水印图像不够清晰,甚至无法进行准确的识别。在压缩攻击算法中,本文算法可以提取到清晰的水印,而FrWT算法提取的水印虽可识别,但是存在一定的模糊性,效果相对较差,FrDCT提取到的水印难以识别。 图6实验对比结果通过视觉方式对算法的水印检测性能进行了验证和对比,是一种定性分析结果。下面从定量角度对算法的水印检测性能进行实验验证和对比,结果如表1所示。 表1 水印检测性能量化对比 根据表1实验结果可知,对于选取的集中攻击类型,本文算法对于水印检测的效果均要优于选取的文献[14-15]两种对比算法。根据以上实验结果,本文所提算法在水印图像检测过程中相对于选取的文献[14-15]两种对比算法具有更高的抗攻击能力和鲁棒性。 本文提出一种基于搜索优化改进坐标法的退化压缩感知水印检测算法,以最小化失真作为优化指标,采用检测概率为特征的检测可靠性约束,进行最优测量次数(提供带宽)和嵌入强度的优化。采用图论处理方式进行坐标搜索算法的优化过程改进,获得一组能够符合约束限制的解集,实现对水印检测算法性能的提升。存在的问题:1) 本文算法侧重于过程的实现和实验的验证,在理论分析方面稍显不足;2) 算法在实验室条件下得到了很好的验证,对于真实应用场景的效果,有待于进一步验证。这两方面是今后研究的重点。3.2 改进坐标优化算法

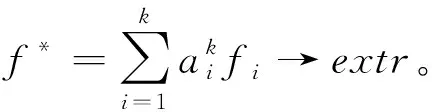

4 实验结果
4.1 水印检测:求最佳参数设置



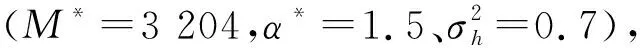

4.2 抵御攻击测试





5 结 语

