基于神经网络的金融市场艾略特波浪识别

李音润 欧 鸥

(成都理工大学信息科学与技术学院 四川 成都 610059)

0 引 言

随着机器学习、人工神经网络、强化学习和深度学习等人工智能技术的发展，人工智能技术被成功应用于图像处理、语音识别和自然语言处理等领域。人工神经网络属于机器学习领域的一个分支，具有非线性、自适应的分布式并行结构，可用于解决分类和回归问题。

金融市场结构复杂、波动频繁的特点受人类社会经济和自然各方面因素影响。大量复杂的变化因素导致研究分析市场行为的困难增加。艾略特波浪理论被成功应用于金融市场的分析。该理论由R.N.艾略特[1](Ralph Nelson Elliott)提出。艾略特认为金融市场的波动行为遵循一定的模式，仅在范围和时间上有区别，他将这类模式定义为“艾略特波浪”。此外，波浪理论不仅适用于描述交易市场的变化行为，还可正确描述人类群体性行为以及各种自然现象，因此又称之为“自然法则”。

尽管艾略特波浪理论具有较高的准确性，但目前国内学者对它的研究较少，将人工智能应用于该理论的研究更是寥寥无几。鉴于这种现状，本文提出利用人工神经网络技术，从金融市场的历史数据中识别、提取出艾略特波浪模式。本文介绍了两种基于人工神经网络的技术——传统的后向传播神经网络和模糊神经网络，并根据这两种技术设计出识别艾略特波浪模式的分类器。传统后向传播网络在研究和实验过程中表现了一些缺陷，于是在传统后向传播网络的基础上引入了模糊神经网络。本文引入的模糊神经网络在学习算法、网络结构等方面对传统后向传播网络进行改进，并通过实验验证和比较了两种分类器的识别效果。

1 相关研究

文献[2]最早提出了分析和预测金融市场变化的模型——ARIMA模型，该模型采用时间序列表示金融市场的历史交易数据，包括自回归、差分和平均移动三个部分。ARIMA模型的提出奠定了金融市场模型研究的基础。此后，涌现了大量基于时间序列的预测模型，Gooijer等[3]对这些模型做过系统性总结和比较。

金融市场预测模型的技术热点主要在机器学习领域，包括人工神经网络、支持向量机、贝叶斯方法、决策树等，以及在此基础上，多种方法相结合的混合技术。市场的预测对象主要有价格预测和趋势预测。相比之下，趋势预测的可行性和实用性更高。

近年来，利用人工神经网络技术建立金融市场预测模型的研究热度很高。技术包括多层感知机(MLP)、动态人工神经网络(DAN2)和混合神经网络[4]。概率神经网络(PNN)在预测股票指数的未来变化方向上表现良好[5]。此外，Manahov等[6]使用基于强类型遗传规划(STGP)的算法对富时100指数、标准普尔500指数及罗素3 000指数进行分析，发现了股票市场的动态和非线性结构。

除人工神经网络的方法外，支持向量机[7]、模糊系统[8]和基于多种理论的混合模型[9]，经过实验证明，也具有较高的可靠性。

随着深度神经网络技术[10]的发展，文献[11]提出了一种基于深度学习的高频策略，并用实验证明，该策略的定向精度高达66%。Chong等[12]比较和总结了1980年至今提出的各种股票市场预测模型，并将深度学习系统地运用在股票市场的分析和预测上。

根据时间的变化范围，可将股票市场的预测分为两类——长期和短期。长期预测通常指在周、月、季及年的时间范围内进行价格或趋势预测，短期预测指对分钟、小时及当日交易的预测。多数研究者更关注短期预测[11-13]，即高频交易。

根据Prechter[14]对艾略特波浪理论和股票市场波动的描述，我们可以得出结论，艾略特波浪比纯粹的股票价格信息更能反应金融市场的本质，正确识别艾略特波浪模式即可正确判定未来市场走势。使用艾略特波浪理论可实现对金融市场价格和趋势的全面预测，该理论对长期和短期的市场变化均适用。不同于上述这些利用股价数据直接分析预测金融市场的技术，本文关注于艾略特波浪模式的识别。

2 后向传播神经网络

2.1 传统的后向传播神经网络

后向传播神经网络是采用后向传播算法作为学习算法的一种人工神经网络。神经网络具有并行的分布式层次结构，每层由多个非线性运算单元(即神经元)构成。神经元对输入信息进行加权，结合偏移量(或称“阈值”)，通过非线性函数产生对应的输出结果。底层的输出结果作为高层的输入数据，进而实现从大量输入数据中发现分布式特征的目的。神经元使用的非线性函数被称作激活函数，sigmoid函数是其中最常用的一种。对第i个神经元使用sigmoid函数进行运算处理由公式表示：

(1)

式中：xj表示输入神经元i的第j个数据，wij表示由上一层神经元j至本层神经元i的连接权重值，bi表示神经元i的偏移量。

后向传播神经网络通过前向传播得到输出结果，通过后向传播修正权重和偏移量等网络参数。式(1)实现了从输入到输出的前向传播过程。设第i个神经元的预期输出结果为di，单个输入样本k的总体误差函数由公式定义：

(2)

输出层的权重修正公式：

(3)

式中：δi是输出层单元i的误差项，δi=outi(1-outi)·(di-outi)。

同理可得偏移量的修正公式：

(4)

以三层神经网络为例，hj表示隐藏层的输出值，那么隐藏层的第j个神经元的误差项由公式表示：

(5)

学习率η越高收敛速度越快，但会导致振荡现象。引入动量因子α可削弱振荡现象则有：

Δwij(n)=ηδixj+αΔwij(n-1)

(6)

n表示当前的迭代次数。隐藏层的权重值、偏移量的修正公式与式(3)、式(4)类似。迭代进行上述操作。

2.2 传统后向传播神经网络的问题

后向传播神经网络存在以下三个问题[15]：

• 后向传播算法可能得到局部最优结果，即不能保证收敛结果是全局最优[15]；

• 对隐藏层神经元的分析通常比较困难；

• 算法的收敛速度较慢，收敛速度受权重的影响较大。

为改进传统后向传播神经网络，提高收敛速度并保证网络的稳定性，本文在传统后向传播算法的基础上引入了缩放共轭梯度算法SCG(Scaled Conjugate Gradient)。

另外，在金融市场的实际交易中，当前价格所处的艾略特波浪有多种可能且发生概率相同，这便引入了分类边界模糊的问题。模糊理论是解决这类问题的有效方法。

考虑到以上两大问题，本文将缩放共轭梯度算法和模糊理论引入传统后向传播神经网络，提出第二种基于人工神经网络的艾略特波浪模式分类器。这便是下面介绍的基于SCG算法的模糊神经网络。

3 模糊神经网络

3.1 模糊理论

模糊神经网络是结合了模糊理论的人工神经网络。模糊算法是基于if-then规则的分类器，该算法遵循模糊理论的规则。模糊理论由Zadeh[17]提出，是关于模糊集和隶属函数(membership function)的分析方法。模糊集通过隶属函数实现边界定义模糊的分类，即某个数据可以同时隶属于多个类。使用模糊神经网络，元素(即数据)的分类结果由隶属度表示。论域中每个元素对模糊集的隶属度由隶属函数计算得到。已知论域U，函数μM(·)可将论域U映射至[0,1]，论域U上的模糊集M由下式定义：

M={〈μ,μM(u)〉|u∈U}

(7)

式中：函数μM(·)是模糊集M的隶属函数，论域的元素u∈U进行隶属函数μM(·)映射后得到的值被称为元素u对模糊集M的隶属度。

常见的隶属函数有以下四种：

• 三角形隶属函数：

• 高斯隶属函数：

• 钟形隶属函数：

•sigmoid隶属函数：

其中，{a,b,c,d,δ}为上述隶属函数的参数。

图1展示了一个基本的模糊系统。

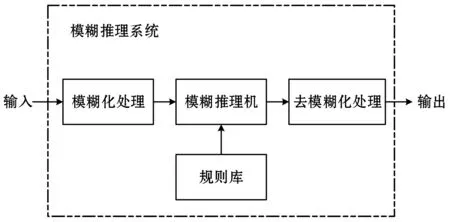
图1 简单的模糊系统

根据模糊规则的不同，可将模糊系统分成多类，其中应用最广的是Mamdani模糊系统、Sugeno模糊系统和Tsukamoto模糊系统。

以Sugeno模型为例，对于有两个输入(x,y)和单输出z的一阶Sugeno模型，其if-then规则集有：

• 规则1：ifx是A1andy是B1，thenz=f1(x,y)=p1x+q1y+r1；

• 规则2：ifx是A2andy是B2，thenz=f2(x,y)=p2x+q2y+r2；

3.2 基于SCG算法的模糊神经网络

为了将模糊理论与神经网络相结合，张智星等[18]提出了神经-模糊系统(简称ANFIS)。该系统有五层网络结构。以Sugeno模糊系统为例，设有两个输入(x,y)，ANFIS的结构如图2所示。

图2 具有两个输入的ANFIS结构[18]

网络的第1层计算输入对模糊集的隶属度，实现模糊化处理；第2层计算规则1和规则2的激励强度；第3层计算每条规则的激励强度与所有规则的激励强度的比值，实现激励强度的归一化；第4层根据Sugeno模糊规则设定三个参数{pj,qj,rj}，该层由具有激活函数的自适应单元组成；第5层计算总输出。用Oi,j表示第i层的第j个单元的输出值，各层操作如下所示：

• 第1层：O1,j=μA,j(x)j=1,2

O1,j=μB,j-2(y)j=3,4

• 第2层：

O2,j=wj=μA,j(x)μB,j(y)j=1,2

• 第4层：

• 第5层：

ANFIS网络需要训练和修正两类参数——前提参数和结论参数，即隶属函数中的参数和根据模糊规则设定的参数。文献[18]认为，当前提参数取固定值后，最终的输出可由结论参数的线性组合表示，如公式所示：

(8)

ANFIS网络由前向传播和后向传播组成。前向传播的输出值由式(8)得到。后向传播迭代修正权重值的基本公式如下：

wk+1=wk+ηkPk

(9)

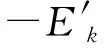
(10)

CG算法在迭代过程中通过线性搜索确定步长，会消耗大量时间。为解决该问题，文献[19]提出了缩放共轭梯度法(SCG算法)。该算法引入尺度因子λk，用Hk+λkI代替单纯的Hessian矩阵Hk。SCG算法的步长公式为：

(11)

基于SCG算法的神经网络大大加快了收敛速度，同时保证了网络的稳定性。从理论上讲，该网络的实用效果，应该优于传统后向传播网络。

4 艾略特波浪理论

艾略特波浪理论的基本思想源于分形理论和斐波那契数列。R.N.艾略特通过对道琼斯工业平均指数的研究，发现金融市场的波动是有韵律的循环行为，他提出用波浪(即艾略特波浪)来描述这种变化行为。一个完整的循环波浪由驱动浪和调整浪组成。驱动浪由五个浪组成,调整浪由三浪或其变体组成,图3展示了调整浪为锯齿形的循环波浪。“调整”是对部分“驱动”价格的回撤，这种部分回撤的关系满足黄金分割率。

金融市场不断重复图3的波浪行为，因此只要确定市场当前价格所处的波浪位置，即可正确预测市场的未来走势。利用神经网络对艾略特波浪理论建模的关键在于正确识别并提取波浪模式。

(a) 牛市里的循环波浪

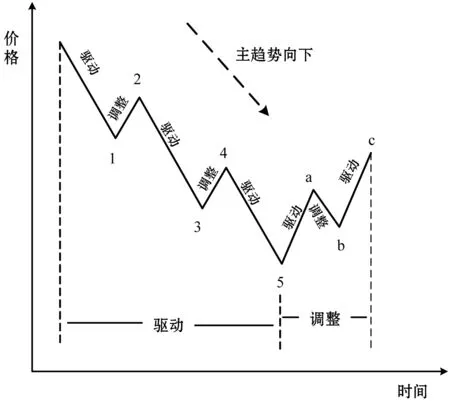
(b) 熊市里的循环波浪图3 完整的循环波浪

根据驱动浪由五个浪组成，调整浪由三个浪组成的原则，图3中的浪1、3、5及浪a、c可细分为5个更小级别的波浪，浪2、4及浪b也由3个更小级别的波浪组成。于是，以图3-a的浪Ⅰ为例，浪Ⅰ可由图4所示的结构表示。

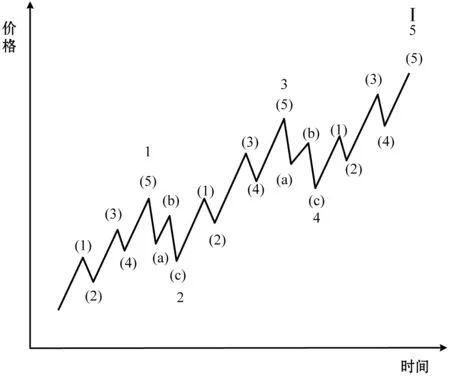
图4 艾略特波浪的分形结构

虽然图4的波浪形态比图3的复杂，但波浪的基本结构相同，即都由驱动浪和调整浪组成。从本质上讲，这种特性遵循了分形理论的自相似性。“分形”由文献[20]在研究英国海岸线时提出。艾略特在分形理论的基础上，提出了“分形级别”的概念，分形级别由波浪规模和时间范围决定。图4中浪Ⅰ的分形级别就比浪1、浪2、浪3、浪4、浪5的大一级。波浪的分形级别在小时图、日图、周图等不同时间范围的K线图中表现尤为显著。文献[14]中还提到，只要不终止金融市场的交易行为，波浪的分形级别就会随时间推移而不断增长。而且这种增长符合对数螺线的变化规律。能否正确区分波浪的分形级别是预测市场未来走势的关键任务之一。

艾略特波浪具有三个不变准则[1]：

• 浪2的运动不会超过浪1的起点；

• 浪3不会是五个浪中最短的；

• 浪4不会进入浪1的价格区域。

以上三个准则适用于规则的波浪，即除不规则三角形以外的波浪。

驱动浪分为常规推动浪和倾斜三角形两类，形式简单，均由向上(或向下)的五个波浪组成。调整浪的形式较为复杂，以主趋势向上的调整浪为例，可将调整浪分为图5所示的三类。

图5 调整浪在熊市中的三种基本形式

以上三类只是调整浪的基本形式，每一类都具有相应的变体形式，例如，平台形的调整浪又有扩散平台形和顺势平台形之分。由于调整浪的形式多变，在解决实际问题时，正确区分调整浪结构的难度大。

以上三类调整浪的子浪结构如表1所示。

表1 三类常规调整浪的子浪结构 个

斐波那契数列是线性递推数列：1，1，2，3，5，8，13，21，34，55，…,数列由下式定义：

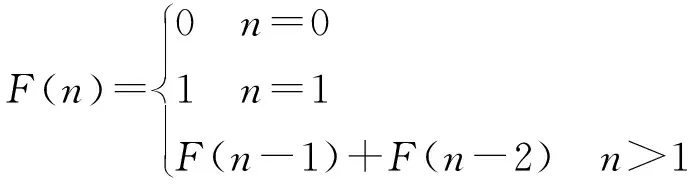
(12)

式中：前一项与后一项的比值无限趋近黄金分割比率0.618。

艾略特波浪理论在多方面体现了斐波那契数列的特点，最主要表现在波浪数和价格比例关系上。艾略特波浪的数目属于斐波那契数列(如表2所示)，调整浪的价格的波动幅度与前一驱动浪的关系通常是0.618或0.382。

表2 波浪数和循环数 个

5 艾略特波浪模式分类器

5.1 数据处理及模式设定

艾略特波浪理论单纯以股票交易日的最高价与最低价为研究对象，在股票价格指数、期货、商品指数等稳定成熟的金融市场上表现良好。实验采取启发式方法，以专家知识为基础，从道琼斯工业平均指数、标准普尔500指数、上证指数、深证综合指数及CRB指数中选取了以图6为例的股价数据作为训练集和测试集。股价的变化范围覆盖分钟、小时、日、周、月和季度。

图6 训练集包括的14种艾略特波浪模式

首先对股价数据进行预处理。股价数据由时间序列(x1,x2,…,xn)表示，利用min-max标准化方法对时间序列作归一化处理，将股价数据映射至[0,1]区间。训练集和测试集由归一化处理后的时间序列组成。min-max标准化表示为：

(13)

训练集的选取对于神经网络的训练结果影响较大，选取适当的艾略特波浪是保证网络识别效果的关键任务之一。依据驱动浪和调整浪两类波浪的规则分别对波浪模式进行分类是最直观的方法，但这种分类方法存在两个问题：

• 调整浪的组成结构复杂、变形多，准确识别调整浪模式的难度较大；

• 调整浪和驱动浪的波浪数目一般不同，导致网络输入层的设置困难。

调整浪的子浪结构虽然复杂，但其整体结构总保持三浪不变。即使是三角形的调整浪，从一定程度上也可划分为A-B-C的三浪结构。驱动浪则总是以五浪的形式展开。考虑到以上因素，实验选择识别的每个波浪模式均包括驱动浪和调整浪，即以完整循环浪为识别目标。通过对艾略特波浪理论和股票指数的分析、研究，实验选取最常见的四种驱动浪和五种调整浪结合，设计了14种波浪模式(如图6所示)。在驱动浪中，最常见的情况是第三浪和第五浪延长，因此实验选取以下四种驱动浪：

• 第三浪延长，且第一浪和第五浪等长(模式1-3)；

• 第三浪延长，且第五浪的长度为第一浪的0.618倍(模式4-5)；

• 第五浪延长(模式6-10)；

• 三角形驱动浪(模式11、13)。

实验选取的调整浪有以下四种：

• 锯齿形(模式1、6和模式11-14)；

• 平台形(模式2-5和模式7-10)；

• 衰竭形(模式3、5、8、10)；

• 三角形(模式12、14)。

实验将上述几种驱动浪和调整浪进行组合，得到图6的14种波浪模式。训练集和测试集选取的时间序列均包含图6所示的波浪模式。

5.2 基于后向传播神经网络的分类器

本次实验的目的是利用后向传播神经网络，从给定的金融时间序列中，分类识别出艾略特波浪模式。

实验采用9-10-14的三层后向传播神经网络架构，即输入层有9个神经元，隐藏层有10个神经元，输出层有14个神经元。每个样本的输入向量包括9个元素(x1,x2,…,x9)。输出向量包括14个元素，每个元素依次代表对应的模式类别。该网络是全联通的，初始权重为随机值。为适应和修正网络参数，设置学习率为0.2，不考虑动量因子，经过1 600次迭代训练后的网络的总体误差趋于稳定，均方误差稳定于0.86。该网络的均方误差变化如图7所示。

图7 基于传统后向传播网络的分类器的均方误差

5.3 基于模糊神经网络的分类器

为有效解决传统后向传播神经网络收敛速度慢的问题，实验选用SCG算法作为模糊神经网络的学习算法。SCG算法的最大优势在于它的参数(包括学习率、动量因子)是完全自动化的，不需要用户设定。

实验设置四层架构的模糊神经网络，选择高斯函数作为隶属函数，输入层由9个单元构成，输出层为1个单元，输出结果是输入时间序列对应的波浪模式类别编号。根据输出的波浪模式类别，实验设定14个规则。实验选定的训练集和测试集与后向传播神经网络的相同，经过对模糊神经网络的120次迭代训练后，网络的总体误差趋于稳定，均方误差稳定于0.21。该网络的均方误差变化如图8所示。

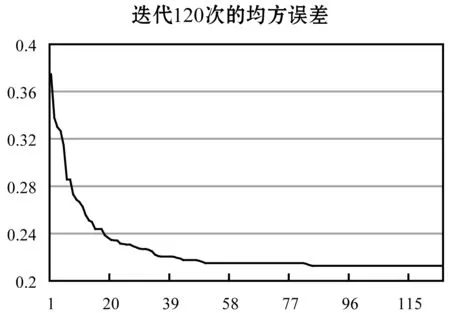
图8 基于模糊神经网络的分类器的均方误差

5.4 实验结果的分析与比较

通过实验证明，基于人工神经网络的技术可以成功从给定的金融时间序列中识别分类艾略特波浪模式。我们从收敛速度和准确率两方面比较了两种算法的实验结果。在评估误差时使用了表3所示的四个评估标准。评估标准的计算公式为：

• 均方误差：

• 平均绝对误差：

式中：N为样本总数，dk,i表示样本k的第i个神经元的预期输出值，outk,i表示样本k的第i个神经元的实际输出值。最大均方误差和最大平均绝对误差分别指整个迭代过程中，均方误差和平均绝对误差的最大值。

表3 实验结果评估标准

使用相同的训练集和测试集进行实验，表4展示了两种神经网络的收敛速度和误差情况。与传统后向传播神经网络相比，基于SCG算法的模糊神经网络的收敛速度提高了92.5%，均方误差降低了75.4%，平均绝对误差降低了70.2%。实验证明，基于SCG算法的模糊神经网络不仅保证了网络的稳定性，还提高了网络的收敛速度和准确率。

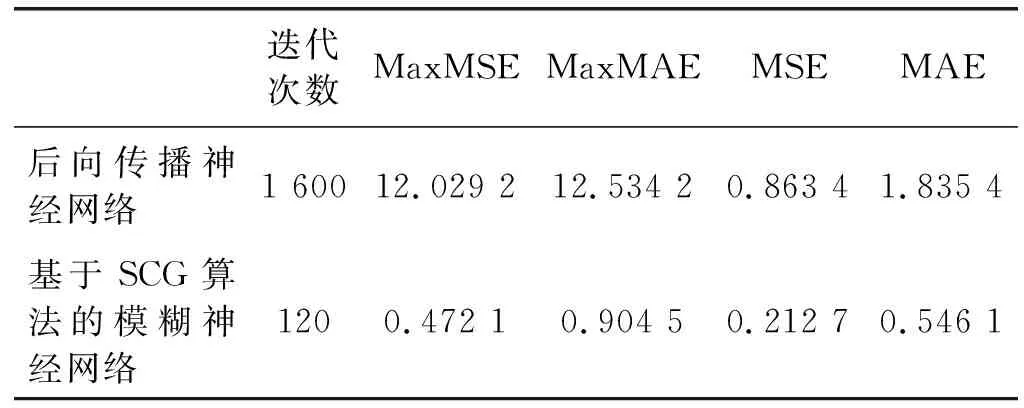
表4 两种人工神经网络识别艾略特波浪模式的效果

6 结 语

本文介绍了后向传播神经网络、模糊神经网络及艾略特波浪理论。提出基于传统后向传播神经网络的艾略特波浪模式分类器，根据传统后向传播网络的缺陷及金融市场的变化特性提出了改进方法——基于SCG算法的模糊神经网络。通过实验，比较了两种分类识别艾略特波浪模式的方法的效果。实验证明了利用人工神经网络技术从金融时间序列中识别艾略特波浪模式的可行性。根据实验数据得出结论，基于SCG算法的模糊神经网络在收敛速度和准确率上的表现均比传统后向传播神经网络更好。但是，本文的研究以专家经验为基础，采取启发式方法选择训练和测试，这可能引入数据不平衡的问题。艾略特波浪理论提供了一个成熟可靠的金融市场分析方法，但国内对该理论的研究较少。目前，利用人工智能技术对金融时间序列的研究较多，缺乏结合艾略特波浪理论这一有效工具的研究。本文仅利用两种神经网络对艾略特波浪做了初步的分类识别，与实现将艾略特波浪理论与人工智能方法融合的目标还有一定差距。下一步将注重于调整网络深度、优化网络参数。考虑到分形理论是艾略特波浪理论的基础，接下来还将尝试结合分形网络模型(FractalNet)实现艾略特波浪的识别。