基于邻域组合熵的属性约简算法

王 光 琼

(四川文理学院智能制造学院 四川 达州 635006) (达州智能制造产业技术研究院 四川 达州 635006)

0 引 言

粗糙集作为一种处理不确定性信息的有效数学工具，已经广泛应用于机器学习、知识发现和规则提取等领域[1-3]。经典粗糙集以完备信息系统为研究对象，通过严格的等价关系对论域进行划分，要求所有属性值都是离散型的。然而，实际应用中，来自教育、医疗和金融等领域的数值型数据很多，经典粗糙集不能直接处理属性值有数值型数据的信息系统，为了解决此问题，Lin[4]对等价关系进行扩展，提出了邻域关系。邻域关系能够处理同时有名义性和数值型数据的混合型信息系统，因此基于邻域关系的邻域粗糙集模型得到广泛应用[5-6]。

属性约简是粗糙集领域中研究的关键问题之一，目的是在不影响系统分类能力的前提下剔除冗余的条件属性。为了对信息系统进行属性约简，从信息论的角度出发，文献[7]提出了基于信息熵的决策表约简算法;文献[8]提出了基于条件信息熵的决策表约简；文献[9]提出了基于边界域的条件信息熵属性约简算法。以上算法主要处理符号型数据，不能直接处理数值型数据或者符号性和数值型混合的数据。为了解决此问题，借助邻域关系可以处理混合数据的特点，文献[10]提出了一种基于邻域熵的属性约简算法；文献[11]提出了邻域决策错误率的局部约简算法；文献[12]提出了基于邻域组合测度的属性约简算法。此外，在粗糙集理论中，不确定性分为知识不确定性和集合不确定性。目前提出的属性重要度度量大多仅考虑知识不确定性或者集合不确定性，同时考虑两者的不确定性来定义属性重要度度量进而设计属性约简算法是研究的热点。

本文以邻域信息系统为研究对象，以邻域关系为基础，为了描述知识对系统的划分能力，首先定义了邻域条件熵。为了从知识不确定性和集合不确定性两个方面来综合度量属性的重要度，将邻域条件熵与邻域近似精度结合，定义了属性重要度度量——邻域组合熵，并提出了基于邻域组合熵的属性约简算法。该算法可以处理离散型和数值型并存的不完备邻域信息系统。最后实验验证了本文所提算法的有效性。

1 相关概念

特别地，若A=C∪D，C为条件属性集合，D为决策属性集合，则称DNI=(U,C∪D,V,f,δ)为邻域决策信息系统。若用“*”表示缺失值，∀a∈A，存在f(x,a)=*，则称NI为不完备信息邻域信息系统。

定义2设邻域信息系统NI=(U,A,V,f,δ)，定义属性子集B⊆C上的δ的邻域关系为：

NRδ(B)={(x,y)∈U×U|DB(x,y)≤δ}

(1)

式中：DB(x,y)表示对象x和y在属性子集B上的距离。显然，邻域关系满足自反性和对称性。为了可以处理离散型和数值型并存的不完备邻域信息系统，本文中的距离采用文献[13]中的距离函数。设属性子集B={a1,a2,…,am}，距离度量为：

式中：1≤l≤M。

当al为名义性属性时：

当al为数值型属性时：

定义3设邻域信息系统NI=(U,A,V,f,δ)，∀x∈U，x关于B的邻域为：

(2)

性质1设邻域信息系统NI=(U,A,V,f,δ)，∀x∈U，对于P,Q⊆A，有：

定义4设邻域信息系统NI=(U,A,V,f,δ)，对象集X⊆U关于属性子集B⊆C的上、下近似和边界域分别定义如下：

(1)X的上近似：

(3)

邻域近似精度刻画了信息系统中对象集合的不确定性，其值一般随着属性子集的增大而增大，因此成为一种重要的不确定度量工具。然而，邻域近似精度并不具有严格的单调性，也存在属性子集增大，其值不变的情况。

2 邻域条件熵以及邻域组合熵

为了从知识不确定性和集合不确定性两个方面来度量属性重要度，本节定义了邻域条件熵，并结合邻域近似精度定义了邻域组合信息熵。

(4)

信息熵KN(B)反映了属性子集B对系统论域中对象的区分能力，KN(B)的值越大，属性子集的区分能力越好。

定义7设邻域信息系统NI=(U,A,V,f,δ)，P,Q⊆C，知识Q关于P的邻域条件熵定义为：

NE(Q|P)=NE(Q∪P)-NE(P)

(5)

邻域条件熵NE(Q|P)反映了属性集合P对于属性集合Q的不确定性。对于决策邻域信息系统，NE(D|P)则反映了属性集P对于决策属性D的不确定性。

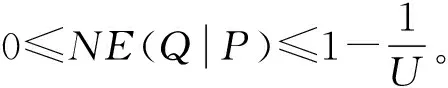
证明:NE(Q|P)=NE(Q∪P)-NE(P)=

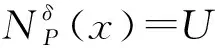
定理2(单调性) 设邻域信息系统NI=(U,A,V,f,δ)，P,Q⊆C，P⊆Q，则有NE(D|Q)≤NE(D|P)。

证明:NE(D|P)-NE(D|Q)=

定理2表明，邻域条件熵具有单调性，熵值随着条件属性集合的增大而减小，条件信息熵越小，则系统协调程度越高。因此在属性约简中，邻域条件熵可以作为属性重要度度量的一个重要因素。

其实，属性重要度的度量主要有基于代数定义和基于信息定义的方法[14]。两种方法具有互补的特性，基于代数定义主要考虑的是属性对论域中确定分类子集的影响；基于信息定义主要考虑的是属性对于论域中不确定分类子集的影响。为了同时从基于代数定义和基于信息定义两个方面衡量属性重要度，结合邻域近似精度和邻域条件熵定义新的邻域组合熵。

(6)

邻域近似精度从集合的角度考虑不确定性，邻域条件熵从知识的角度考虑不确定性，因此邻域组合熵同时考虑了集合和知识的不确定性，对不确定性的刻画更加全面。

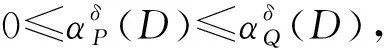
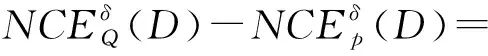
定理3表明，邻域组合熵具有单调性，熵值随着条件属性集合的增大而增大。因此，可以以邻域组合熵来度量属性的重要度，设计基于邻域组合熵的属性约简算法。

定义9设邻域决策信息系统NI=(U,C∪D,V,f,δ)，∀B⊆C，对于属性a∈C-B，a相对于B的重要性定义为：

(7)

定义10设邻域决策信息系统NI=(U,C∪D,V,f,δ)，∀B⊆C，若满足如下条件：

则称属性子集B为C相对于决策属性的一个相对约简。

定义11对于一个邻域信息系统NI=(U,C∪D,V,f,δ)，相对于决策属性D，C中所有必要的属性组成的集合称为C相对于D的核，简称相对核。

3 基于邻域组合熵的属性约简算法(ARNCE)

本节以邻域组合熵为启发信息，提出了一种邻域信息系统的属性约简算法。

算法1为计算邻域组合熵的算法。

算法1邻域组合熵的计算

Step 1 计算邻域条件熵；

foriton

计算p(xi),

Endfor

计算邻域信息熵NE(B)；

计算邻域条件熵NE(D|B)；

Step 2 计算邻域近似精度；

forjtom，

Endfor

算法2为基于邻域组合熵的属性约简算法。算法思想：以空集合为起点，以邻域组合熵对属性重要度的度量作为启发信息，每次选择重要度最大的属性加入约简集，直到所有未被选择的属性都是不重要的。

算法2基于邻域组合熵的属性约简算法

输出：约简集合RED。

Step 1 初始化RED=∅；

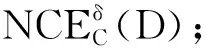
Step 3 Do

对于∀ai∈C-RED，根据算法1计算Sig(ai,RED,D)，

If

Sig(amax,RED,D)=max{Sig(ai,RED,D)|ai∈C-RED}

RED=RED∪{amax}，

Endif

UntilSig(amax,RED,D)=0

Step 4 返回RED；

4 实验结果分析

为了验证本文所提算法处理邻域信息系统的可行性，将本文的算法与以下几种算法分别从属性约简数量和分类精度方面进行比较。

1) 基于邻域依赖度的属性约简算法(DNFS)[15];

2) 基于邻域条件熵的属性约简算法(ARCE)[16];

3) 基于邻域组合测度的属性约简算法(ARNCM)[12]。

由于在属性约简时算法DNFS只考虑依赖度，算法ARCE只考虑了条件熵，而算法ARNCM同时考虑了粒度测度和近似精度。本文算法同时考虑了信息熵和近似精度，所以算法ARNCM和本文算法的时间复杂度要高于DNFS和ARCE。本节主要比较各算法约简后的属性约简数量和分类精度。

本文算法采用Java语言编程实现，硬件环境为：intel处理器3.7 GHz，内存2 GB。

选用UCI中的6个数据集进行实验，其中4个完备数据集，2个不完备数据集。在属性类型方面，数据集Heart、Hepatitis的属性为混合型，数据集Zoo、Soybean的属性为符号型，数据集Wdbc、Sonar的属性为数值型，数据集的具体信息见表1。为了消除各属性量纲不一致对邻域计算的影响，在实验前，对数据集中所有的数值型属性进行标准化处理，统一标准化到[0,1]区间。邻域参数设置为δ=0.15。

表1 UCI数据集中的六个数据集

首先比较各算法属性约简之后的属性约简集大小，实验结果如表2所示。由表2可知，所有算法都能有效地对数据集进行属性约简。算法ARNCE与算法DNFS、ARCE相比，在所有数据集上都获得了相等或者较小的属性约简集。算法ARNCE和算法ARNCM属性约简集大小较为接近，通过对6个数据集的属性约简集大小进行平均计算，算法ARNCM的平均属性约简集大小为6.66，算法ARNCE的平均属性约简集大小为6.33。总体而言，相比较于另外三种属性约简算法，本文所提算法ARNCE能够获得约简集较小的属性约简结果。

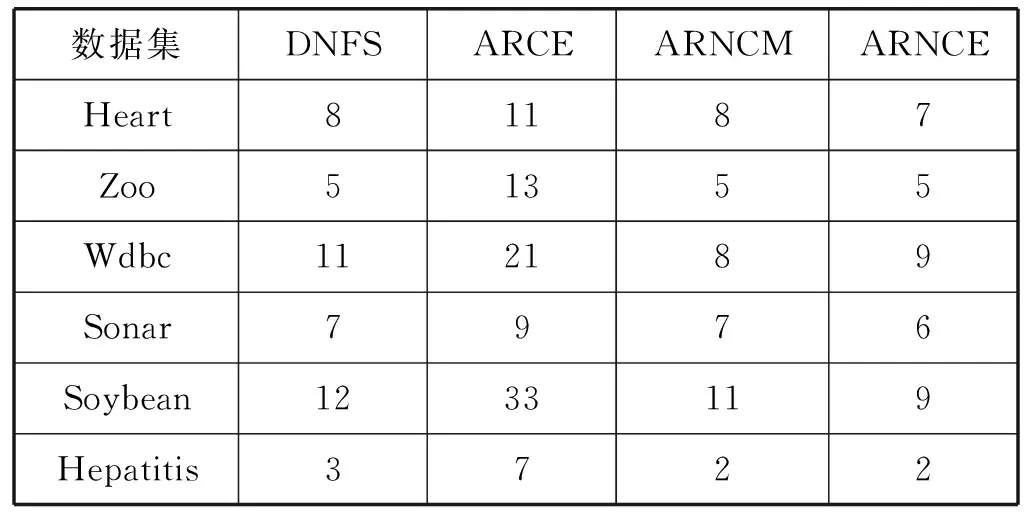
表2 不同算法属性约简后属性约简集大小

为了进一步验证属性约简算法的有效性和分类能力，实验中通过支持向量机(SVM)和决策树(C4.5)两种分类器，采用十折交叉验证的方法，比较各算法约简之后的分类精度，实验结果如表3和表4所示。

表3 基于SVM算法的分类精度比较

表4 基于C4.5算法的分类精度比较

由表3和表4可知：

1) 对于两个混合型数据集Heart、Hepatitis，关于数据集Heart，本文算法ARNCE约简后的分类精度最高；关于数据集Hepatitis，本文算法ARNCE和ARNCM约简后的分类精度相等并且都高于算法DNFS、ARCE。

2) 对于两个数值型数据集Wdbc、Sonar，关于数据集Wdbc，在SVM下本文算法ARNCE约简后的分类精度较高，在C4.5下算法ARNCM约简后的分类精度较高；关于数据集Sonar，在SVM下算法ARNCM约简后的分类精度较高，在C4.5下本文算法ARNCE约简后的分类精度较高。

3) 对于两个符号型数据集Zoo、Soybean，关于数据集Zoo，算法ARCE约简后的分类精度较高；关于数据集Soybean，本文算法ARNCE约简后的分类精度较高。

从整体上看，相比于算法DNFS、ARCE和ARNCM，本文提出的算法ARNCE对大部分数据集进行属性约简后的分类精度较高。

综合上述实验结果可知，本文算法ARNCE能够对邻域信息系统进行有效约简，且能够获得约简集较小、分类精度较高的属性约简结果。

5 结 语

以邻域信息系统为研究对象，本文从信息论角度出发，定义了邻域信息熵和邻域条件熵。结合邻域条件熵和近似精度，定义了邻域组合熵，可以综合知识不确定性和集合不确定性对邻域信息系统属性重要度进行度量，给出并证明了邻域组合熵的相关定理。基于邻域组合熵，提出了邻域信息系统中的属性约简算法。实验结果表明该算法能够获得约简集较小而分类精度较大的约简结果。在关于邻域信息系统的属性约简算法中，邻域参数δ的选取，对约简结果有着很大影响，下一步将对邻域参数δ选取进行研究。