大型活动散场观众交通疏散模型

叶 霞 夏海霞 高志刚

1(浙江理工大学信息学院 浙江 杭州 310018)2(杭州电子科技大学计算机学院 浙江 杭州 310018)

0 引 言

随着城市的发展，大型活动在城市中举办越来越频繁。在活动结束后，观众短时间内大量涌出，受限于观众的步行速度以及道路情况，无法及时地疏散，从而造成严重的交通拥堵问题[1]。目前针对大型活动散场问题的研究通常是建立大型活动观众疏散模型[2-4]，对大型活动散场人流进行仿真[5-7]来预测大型活动散场时的观众疏散情况，没有制定相应的措施解决实际的拥堵问题。为了更好地解决大型活动散场时周围道路的拥堵情况，本文使用共享单车进行临时部署与调度的方式加快观众的疏散，缓解拥堵问题。

从场馆出发到公共交通站点的这段距离被称为“最后一公里”[8-9]。针对“最后一公里”问题，已有许多相关文献提出用公共自行车的方式解决。如文献[10-11]从服务水平和自行车容量考虑，提出自行车共享系统的策略设计模型。文献[12]在北京现有公共自行车站点分布不合理的基础上提出了一种新的自行车部署方案，使其更好地解决“最后一公里”问题。上述文献都是基于日常生活、通勤方面去解决“最后一公里”问题。由于公共自行车有桩模式的限制，目前尚未见到将其应用到大型活动散场疏散问题中的研究。而共享单车的出现，可以很方便地将其部署到需要自行车的地方。针对共享单车的这个特性，本文将其应用到大型活动散场观众交通疏散中，下文将共享单车简称为自行车。

本文针对大型活动散场观众疏散问题，提出了基于人流预测的大型活动散场疏散模型。结合对散场观众流向的预测，使用部署和调度自行车的方式解决“最后一公里”问题，缓解大型活动散场时的短期人流拥堵。实验结果表明，通过本文的模型进行疏散可以提高疏散效率，有效缓解大型活动散场人流拥堵问题。

1 参数及其定义

本节给出了模型中主要的参数和一些定义，参数如表1所示。

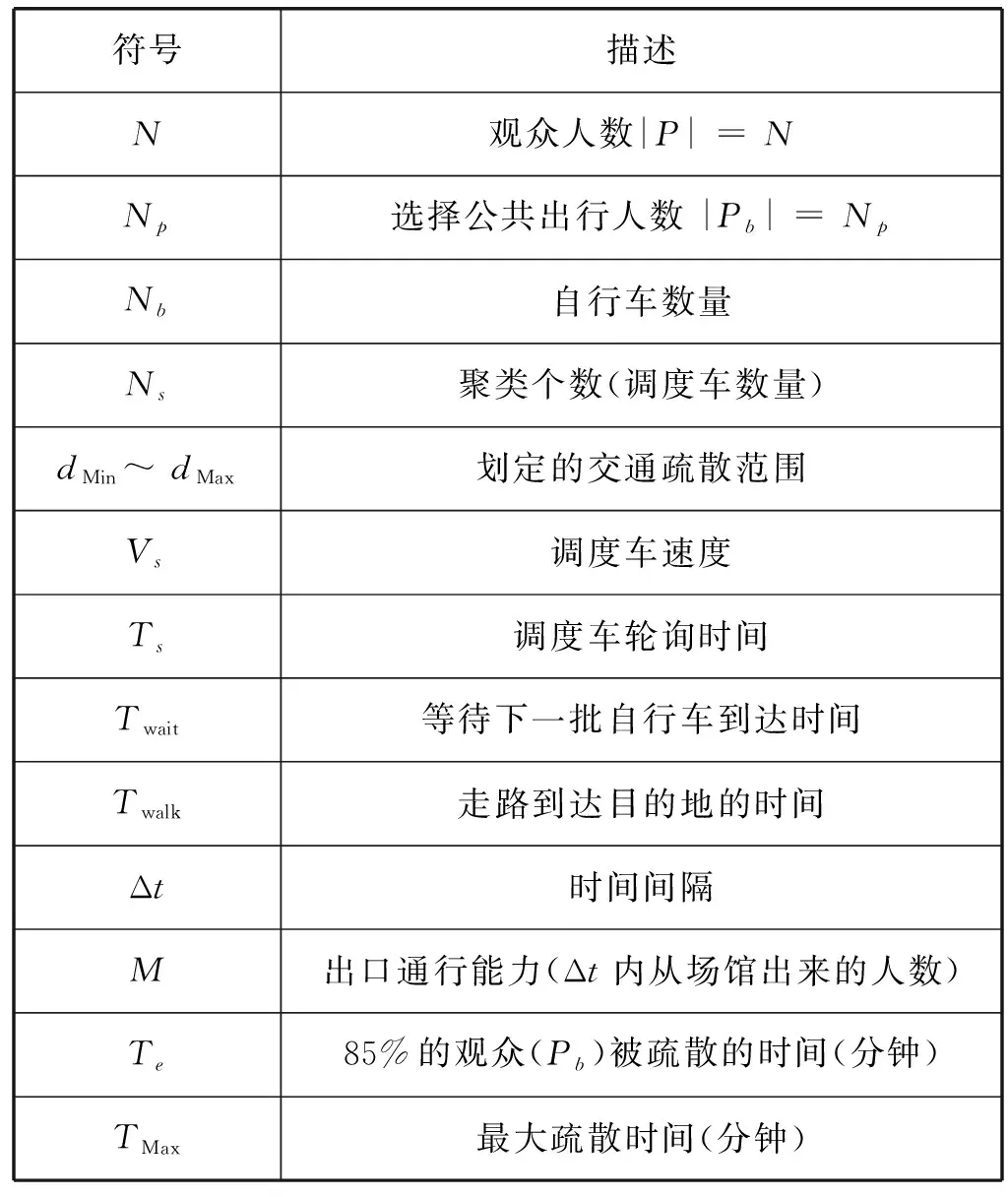
表1 模型参数及其描述

定义1站点集合S。站点包括三类：第一类为起始站点S1，在活动举办场馆出口的主要道路旁部署起始站点，放置自行车；第二类为终止站点S2，大型活动散场时大部分观众选择前往附近的公交站、地铁站(下文统称为公共交通站点)，所以将划定范围内的公共交通站点进行筛选后设定为自行车终止站点S2；第三类为划定范围内的所有公共交通站点，定义为S′。

定义2公共交通站点S′。S′=(ID,Loc,Dis,W)，包括站点ID(唯一标示符)，站点经纬度坐标Loc，站点和活动地实际距离Dis和该站点的运力W。

定义3观众集合P。所有观众中选择自己开车以及场馆内大巴的观众定义为Pa，不在本文疏散的范围内；选择公共出行的观众定义为Pb。Pb=(Vwalk,Vride,Dis,Sp,Se,Tr)，包括观众的步行速度Vwalk；骑车速度Vride；观众从起始点到终止点的OD(from Origin to Destination)距离，即Dis；观众的状态Sp(等待、骑车、走路、到达)；观众是否被疏散的状态Se(观众到达目的地即可认为已被疏散)；被疏散的时间Tr。

2 大型活动散场观众交通疏散模型

2.1 疏散模型框架

大型活动散场观众交通疏散模型框架按照步骤划分，包括以下4个部分：站点部署，人流预测，站点聚类以及调度，基于概率函数的观众选择算法。各模块的功能如图1所示。

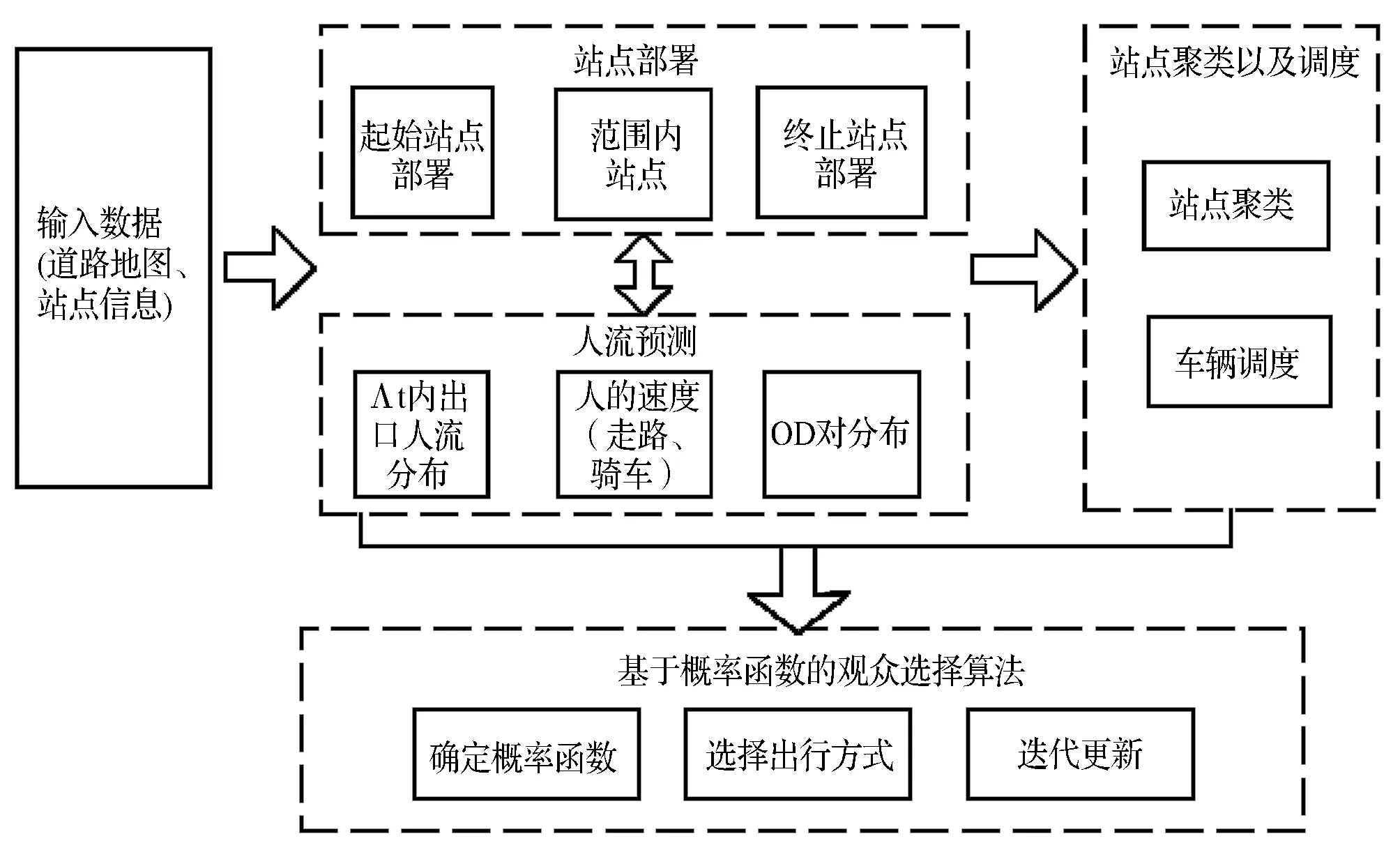
图1 大型活动散场观众疏散模型框架

站点部署：通过活动举办地附近的道路地图、站点信息(包括公交车、地铁路线及其发车时间)确定起始站点和终止站点的部署。

人流预测：根据终止站点的运力以及离活动举办地的距离预测观众的OD分布和站点人流量。根据场馆出口通行能力和观众的OD分布预测Δt时间段内出口的人流分布。

站点聚类以及调度：对所有终止站点进行K-means聚类，适应值函数由站点距离和站点人流量确定。每个聚类分配一辆调度车进行调度。

基于概率函数的观众选择算法：在前面三步的基础上，利用该算法模拟散场观众的疏散情况。根据自行车可用状态，观众等待自行车的时间以及观众走路到达目的地的时间为概率函数去判断观众的出行方式，如此直到疏散完毕。

2.2 站点部署

由定义1可知，起始站点S1设定在活动举办场馆出口的主要道路旁，根据具体场景进行部署，在实验部分讨论。部署初始自行车总量为Nb。

终止站点S2，是将划定交通疏散范围内的公共交通站点进行筛选后得到。对于划定交通疏散范围的确定，文献[8]中提出将5 km作为“最后一公里”的出行界限，其中，中层服务圈是距轨道交通站点1～3 km的自行车出行圈。本文设定dMin=0.5 km，dMax=3 km。

首先将划定交通疏散范围dMin～dMax内的所有公交站、地铁站S′标记出来，然后确定每个站点的运力W。本文定义运力W为公共交通站点单位时间内运输的人数，该人数与站点的公交车数成正比，与发车间隔成反比。同一辆公交车会在各个不同的站点停靠，人们通常会选择最近的站点去乘坐，所以同一辆公交车到达后面站点的可运输人数比前一个站点要大幅度下降。因此，定义每一路公交车属于离活动举办地最近的站点，由此得出每一个公交站拥有的公交车数以及每一辆公交的发车时间间隔。假设一个站点的公交车数为L，该站点每辆公交的发车时间间隔为gi，载客量为hi，计算得到该站点的运力：

(1)

而地铁容量大、速度快、发车时间短，因此单位时间内可以承载更多的客流。假设一列地铁的发车时间间隔为G，载客量为H，可得地铁站的运力：

(2)

最后筛去一些偏僻的站点后，将运力W大于0的站点，定义为终止站点S2。

2.3 人流预测

根据定义3，选择公共出行的观众Pb=(Vwalk,Vride,Dis,Sp,Se,Tr)，本节要预测观众的Vwalk、Vride，Dis以及每个时间段从场馆中出来的观众人数。

其中Vwalk为观众的步行速度，根据已有的行人调查[13]可知，行人速度服从正态分布，即Vwalk～N(u、σ2)。u、σ2分别为平均步行速度及其方差。经测得，人群中行人的平均速度为1.34 m/s, 标准偏差为0.26 m/s。这里的速度是指在道路上不拥堵时的正常步行速度，而在场馆出口拥堵的场景下的步行速度将减慢很多，本文设定场馆500 m范围内的步行速度服从Vwalk～N(0.56, 0.01)。

Vride为观众的骑车速度，据统计，一个人的骑车速度是步行速度的3～5倍，本文假设Vride=4×Vwalk。

根据每个终止站点离活动举办地的距离Dis以及运力W，创建概率分布函数，预测观众流向。对于每一个站点S2，Dis越大，则观众去的可能性越低，人流越少；反之W越大，则观众去的可能性越大，人流越多。因此，本文根据这两个特性定义两个分数来判断人流，一个是距离分数，定义如下：

Sd=1-sigmoid(Dis,a,c)

(3)

(4)

另一个为运力分数，定义如下：

(5)

每一个站点S2的总分数，即为：

Sτ=τSd+(1-τ)Sw

(6)

式中：划定范围dMax=3 km；WMax为最大运力；a，b，c为常量；τ为距离分数和运力分数在总的分数中所占的比重。经多次实验发现，当设定a=2，b=7/20，c=1/2，τ=0.4时，与实际情况最为符合。

最后，根据每个站点分数，进行归一化，得到一个概率函数f，数值越大，即观众去的可能性越大。概率函数如下：

(7)

式(7)得到的概率即为观众去第i个站点的概率，因此，通过多次随机模拟并取平均的方式，得到每个观众到其终点的距离Dis，从而得到所有观众的OD矩阵，由此统计得到各个站点的人流量F。

大型活动散场时，受场馆出口限制，可以简单地认为每个时间间隔Δt内从场馆出来的观众人数等于场馆所有出口的最大通行能力M。每个时间间隔Δt内从场馆出口出来的选择公共出行的观众人数为Pt，并根据最大通行能力M，和公共出行人数Np占总人数N的比例计算得到Pt：

(8)

在每个时间段Δt内，从Np个选择公共出行观众中随机筛选出Pt个观众进行疏散，并在Np个观众中去除已选的观众直至疏散完毕。

2.4 站点聚类以及调度

通过聚类将S2划分为若干块区域，为每一块区域分配一辆调度车，由其负责该区域内自行车的调度。

已知聚类个数Ns，使用K-Means算法对站点进行聚类，得到每个聚类中心点为Ki。Sij表示归属于Ki聚类的第j个站点，假设Ki聚类内有Ci个站点，则：

下面给出该聚类的算法逻辑：

输入：终止站点集合S2，聚类个数Ns，站点人流量F。

Step1随机从输入站点集合中挑选Ns个点，作为初始Ns个聚类中心。

Step2对输入站点集合中的所有点，计算它与所有聚类中心的适应值fitness，计算方式如下：

首先计算聚类中心Ki与其聚类内的各站点Sij的距离之和：

(9)

式中：‖·‖表示计算两个点的距离。

(10)

(11)

因此适应值为：

(12)

Step3更新该聚类中心Ki的位置：定义该聚类内所有站点的几何中心作为新的聚类中心。

Step4重复上述三步，直到聚类中心不再改变。

输出：Ns个聚类集合。

通过结合距离以及人流量，融合多维度的信息进行聚类，能够让各个聚类内的站点距离相对最短，人流量更为平均，分配调度车进行调度的时间可以相应减少，且每辆调度车在一次轮询期间的可调度自行车数最大化。

对这Ns个聚类，安排Ns辆调度车，分派给每个类，根据聚类中心Ki离活动地的距离D和调度车搬运车辆的时间，本文假设为u分钟，计算每辆调度车的轮询时间Ts，其中调度车速度为Vs，即：

(13)

在每个轮询时间内，自行车通过调度车从每个聚类内将结束进程的自行车调度回来，每辆调度车的最大容量为R辆。

2.5 基于概率函数的观众选择算法

本文利用基于概率函数的观众选择算法模拟观众的疏散。已知每个时间段场馆出口的观众分布，根据其目的地距离和等待时间创建概率函数，判断观众的状态Sp(等待、骑车、走路或到达)。具体可能情况如下：

(1) 观众选择骑车并有可用公共自行车，则骑车到达目的地，不需要等待；

(2) 观众选择骑车却无可用自行车，则根据概率函数判断观众是否等待，概率公式如下：

(14)

式中：Twalk为观众走路到达其目的地的时间，即：

(15)

概率越大，表示等待的可能性越大，即观众越有可能选择等待下一批自行车的到来并骑车到达目的地。反之，观众选择走路到达目的地的可能性越大。

基于概率函数的观众选择算法的流程图如图2所示。

图2 基于概率函数的观众选择算法流程图

相应步骤描述如下：

Step1初始化各参数，时间段j，观众i，第j个时间段内的观众人数Pt，观众总人数Np。

Step2分析时间段j内的场馆出口的观众分布。

Step3根据当前自行车数，以及观众i的速度、目的地距离和等待时间判断观众i的状态(等待、骑车、走路)。若观众i选择等待，则将观众i归入第j+1个时间段；若观众i选择骑车或者走路，则根据观众i的骑车或走路速度以及其目的地距离计算其到达目的地的时间。

整个疏散过程如图3所示。

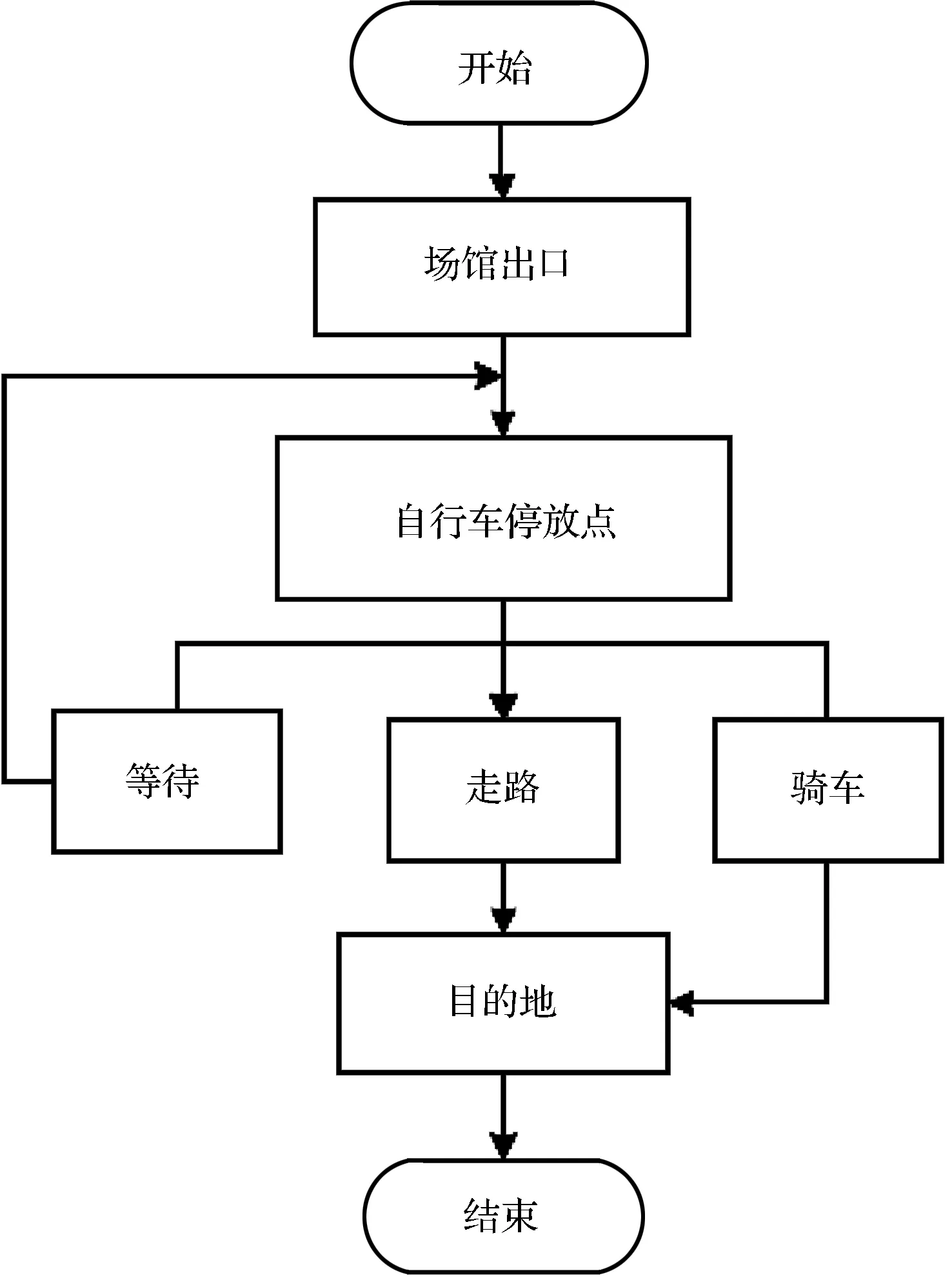
图3 大型活动散场疏散过程

通过优化以下的目标函数确定自行车数量和聚类个数(调度车辆数)。

minC=Cb+Cs

(16)

s.t.

Cb=Nb×cpb

(17)

Cs=Ns×cps

(18)

bMin≤Nb≤bMax

(19)

sMin≤Ns≤sMax

(20)

Te≤TMax

(21)

I≤R

(22)

式中：C为总成本，由两部分组成，第一部分为部署自行车的成本Cb，由式(17)和式(19)可知，Cb为自行车数Nb乘以部署一辆自行车的成本cpb。其中：Nb的取值范围为bMin～bMax，在计算过程中，令100辆自行车为一个单位；第二部分为部署调度车的成本Cs，由式(18)和式(20)可知，Cs为调度车数(聚类数)Ns乘以一辆调度车的成本cps。其中，Ns的取值范围为sMin～sMax；式(21)表示85%的观众Pb被疏散的时间不超过TMax分钟；式(22)表示每个轮训期间到达聚类内的可调度自行车数I小于调度车可以调度的自行车数目R。

对于求解以上式子，疏散时间、疏散人数都需要通过整个模型进行计算得到，所以根据实际的问题，通过不同的Nb和Ns的组合，求出最佳的部署和调度结果。

3 模型仿真实验

3.1 实验准备

本文提出的模型以杭州市黄龙体育场某次大型活动为实验对象，实验环境：Intel四核2.50 GHz处理器、8 GB RAM、Window7系统，编程语言：Python。实验参数见表2。

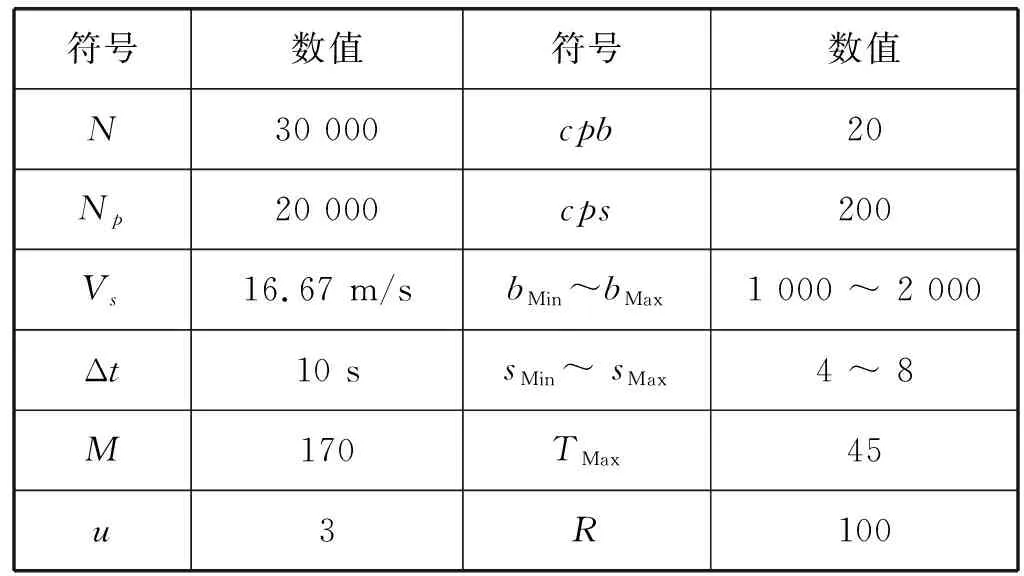
表2 实验参数

根据黄龙体育场的场馆出口主要道路分布图，在场馆的出口的5个道路段分别部署起始站点S1，并平均分配初始自行车，如图4(a)所示。以黄龙体育场为中心划定范围dMin～dMax内的所有公交、地铁站S`标记出来，如图4(b)所示。本文定义每辆公交的载客量都为20，通过分析每个公交站的公交车数以及每辆公交的发车时间间隔，根据式(1)得到每个公交站的运力。根据式(2)计算地铁站的运力。本文定义地铁的载客量为600，地铁发车时间间隔为6分钟。因此由式(2)可以直接得到地铁站的运力为100。然后根据每个站点的运力筛选出终止站点S2，如图4(c)所示。

(a) S1分布图

(b) S′分布图

(c) S2分布图图4 站点分布图

根据站点离目的地的距离以及人流量通过K-Means聚类方法对S2进行聚类，并且分配调度车进行调度。通过基于概率函数的观众选择算法模拟观众的疏散。

3.2 实验结果与分析

本文将以下5种不同的疏散方法进行对比，其中方法5为本文的模型：

《说文》中说：“把，握也。从手，巴声。”可见“把”的本义为“握”“持”，即将物拿在手里，为动词。后来由“握持”义引申为“把持”“控制”“掌管”义。此时“把”的结构形式为把+NP

(1) 全部观众Pb走路到达目的地。

(2) 使用场馆周围原有自行车进行疏散，不进行调度。经统计，场馆周围原有自行车数(包括公共自行车和共享单车)共626辆。

(3) 结合本文方法和文献[14]中的FCM聚类方法进行疏散。

(4) 结合本文方法和文献[15]中的FMM聚类方法进行疏散。

(5) 利用本文的大型活动散场观众交通疏散模型进行疏散。

对于不同的聚类个数和自行车数量组合，对比方法3-方法5的疏散时间Te，结果如图5所示。在不同的聚类个数和自行车数量组合下，本文方法的疏散时间都低于另外两种方法。根据式(16)的目标函数及约束条件，解出最佳的部署、调度方案为自行车数：1 500，聚类数即调度车数量：6，满足疏散时间Te≤TMax，I≤R，且成本最低。

(a) 方法3

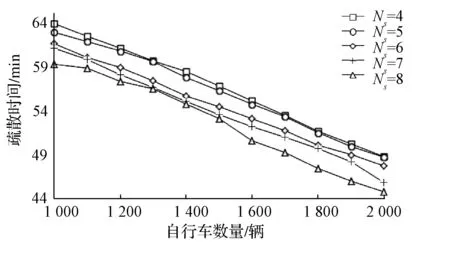
(b) 方法4

(c) 方法5图5 不同组合方案下的疏散时间对比

按上述方案，这5种疏散方法在各个时刻的剩余人数如表3所示。此处剩余人数为未被疏散的人数，即未到达目的地的观众人数。

表3 各个疏散方法下的剩余人数统计 人

对比表3中各个方法在各个时刻的剩余人数，在散场60 min后，5种方法的剩余人数都低于5 000人，而方法3-方法5都低于2 000人。对于方法1和方法2，由于一开始观众大量涌出，且都是通过步行往外行走，到达终点的人数较少，散场30 min内剩余人数减少很缓慢，30～60 min时疏散速度明显加快。方法3-方法5通过部署和调度自行车使得疏散速度在前30 min内远高于方法1、方法2，而方法5在前40 min的疏散效率高于其他几种方法，能在短时间内将观众疏散出去，从而解决大型活动散场时短时间交通拥堵的现象。

本文通过以下3种指标对这5种方法进行对比，进一步分析本文方法和其他3种方法的疏散效果：骑车率；平均到达时间，即观众Pb到达目的地的平均时间；疏散时间Te。实验对比结果见表4。

表4 实验对比结果

由表4可以看出，方法5的骑车率远高于方法2，且比方法3和方法4提高了17%左右。而有调度的方法3-方法5的平均到达时间明显低于没有部署、调度的方法1、方法2。由疏散时间Te可知，方法5的疏散效率高于其他4种方法，能够起到加快大型活动散场观众疏散的效果，使得原本需要64 min的疏散时间降低到了44 min，且优于方法3和方法4。

4 结 语

本文提出了大型活动散场观众交通疏散模型。通过最优化成本目标函数确定自行车数和调度车数，通过部署和调度自行车的方式对观众进行疏散。并提出了基于概率函数的观众选择算法模拟观众的疏散。以黄龙体育场某次大型活动为实验对象进行仿真实验。实验结果表明，利用本文模型进行疏散的时间比其他4种方法都要短，且比使用活动举办地附近原有自行车进行疏散的时间降低了31.4%。

本文模型简化了调度自行车的方法，下一步的研究可以改进调度方法，提高自行车可用率，从而提高骑车率，缩短疏散时间。