考虑多因素条件下的择期手术排程约束规划模型
孟凡睿 陈淮莉
(上海海事大学物流科学与工程研究院 上海 201306)
0 引 言
医疗卫生行业的发展在我国一直是社会关注的焦点。尽管医疗体制改革正在日益深化,但是人口基数大与人口老龄化现象逐渐加剧的社会现状,仍旧造成了社会医疗资源严重紧缺的问题。手术室作为医院资源存在最为密集的地方,其投入资金占医院财政支出的10%[1],利润占医院总盈利的40%[2]。据不完全统计,手术的进行会关系到医院70%的部门[3]。因此,对手术室的合理利用可以有效地提高资源利用率,从而降低医院的运营成本。
择期手术排程,即在一个排程周期内对已知将要进行的手术在有限的手术室及医护人员等资源下进行合理安排。几十年来,诸多学者从多种角度对该问题进行了研究。文献[4]首先提出将手术排程分为前期计划和分配排程,前期计划即为确定某台手术的手术日期,而分配排程则是就某一天的所有手术进行排序,即确定手术的开始时间。文献[5]将待手术的患者按病情严重程度划分为不同的优先级,在考虑医护人员加班和手术延期的双重成本下进行择期手术日期指派,并依照优先级进行手术。文献[6]在模型中考虑了术前准备时间及术后清洁时间,使模型更贴近实际手术流程。文献[7]将不同技术类别的医护人员,如麻醉师、医生、护士组成一个手术小组,在手术室优化与调度的同时完成了医护人员的调度。文献[8]基于防止医护人员因过劳而造成医疗事故,引入了休息日等限制条件,使得手术排程更人性化。文献[9]在考虑医护人员和医疗器械的资源限制下,研究了多手术室调度问题,建立了最大化患者满意度和最小化医院运作成本的多目标数学模型。
在解决问题的方法上,文献[10]在MIP模型中利用0-1变量确定某一天内的手术和手术室的匹配情况。文献[11]开发了改进的遗传算法,目标是提医疗器械的使用效率,减少患者的等待时间。文献[12]采用蒙特卡洛模拟来评估手术顺序在诸多方面产生的影响,并基于此提出了一种“按手术时长分类排程”的方法,并采用蒙特卡洛模拟,取得了较好的研究成果。文献[13]将手术排程抽象为柔性车间调度问题,建立了两阶段随机规划模型,并先后开发了遗传算法和启发式决策规则以求解手术开始时间和麻醉复苏床位的使用时间。文献[14-15]利用不同的改进遗传算法分别对医患满意度和手术室利用效率进行了优化。
针对这一典型NP-hard问题,前人多是考虑单一手术阶段且利用遗传算法等智能算法来解决。本文将综合考虑上述多种影响因素,采用约束规划模型和ILOG CPLEX中的CP求解器,对手术及手术室的匹配,手术与麻醉恢复床位的匹配,以及单一手术室内的手术顺序进行决策,以实现手术室的高效利用。
1 问题描述与假设
1.1 问题描述
本文综合考虑手术和术后观察两个阶段。对于手术室而言,手术阶段又包括术前准备、手术执行以及术后清洁。以一个工作日为排程周期,对单日内开放的所有手术室和麻醉恢复室床位与预先确定的待执行手术进行匹配。所有手术室为有差别资源,由于配备的医疗器械类型不同等,可接纳的手术类型也不同。同时手术的分配还受执刀医生的影响,执刀医生不能同时进行两台以上的手术。在手术与手术室的匹配确定之后,对单一手术室内将进行的所有手术进行排序,根据手术类型的不同,两台连续进行的手术之间存在时长不等的准备时间。根据实际医院对手术的管理规定,手术的执行具有优先级,对于择期手术而言,时间较长,难度较大的手术具有高优先级,对手术室造成的污染程度最高的手术具有最低的优先级,高龄和低龄患者的手术具有较高优先级。在术后阶段,大部分全身麻醉或术后未能达到意识恢复标准的患者需要在麻醉恢复室(PACU)进行生命体征的观察。国内大型医院的麻醉恢复床位数量约为手术台数量的一半,因此只有PACU有空余床位时,患者才可以被转送去PACU,否则要在手术室滞留,直至有空余麻醉恢复床位。每台手术的两阶段手术流程如图1所示。如果手术安排不合理,就会导致手术室和麻醉恢复床位利用率低。
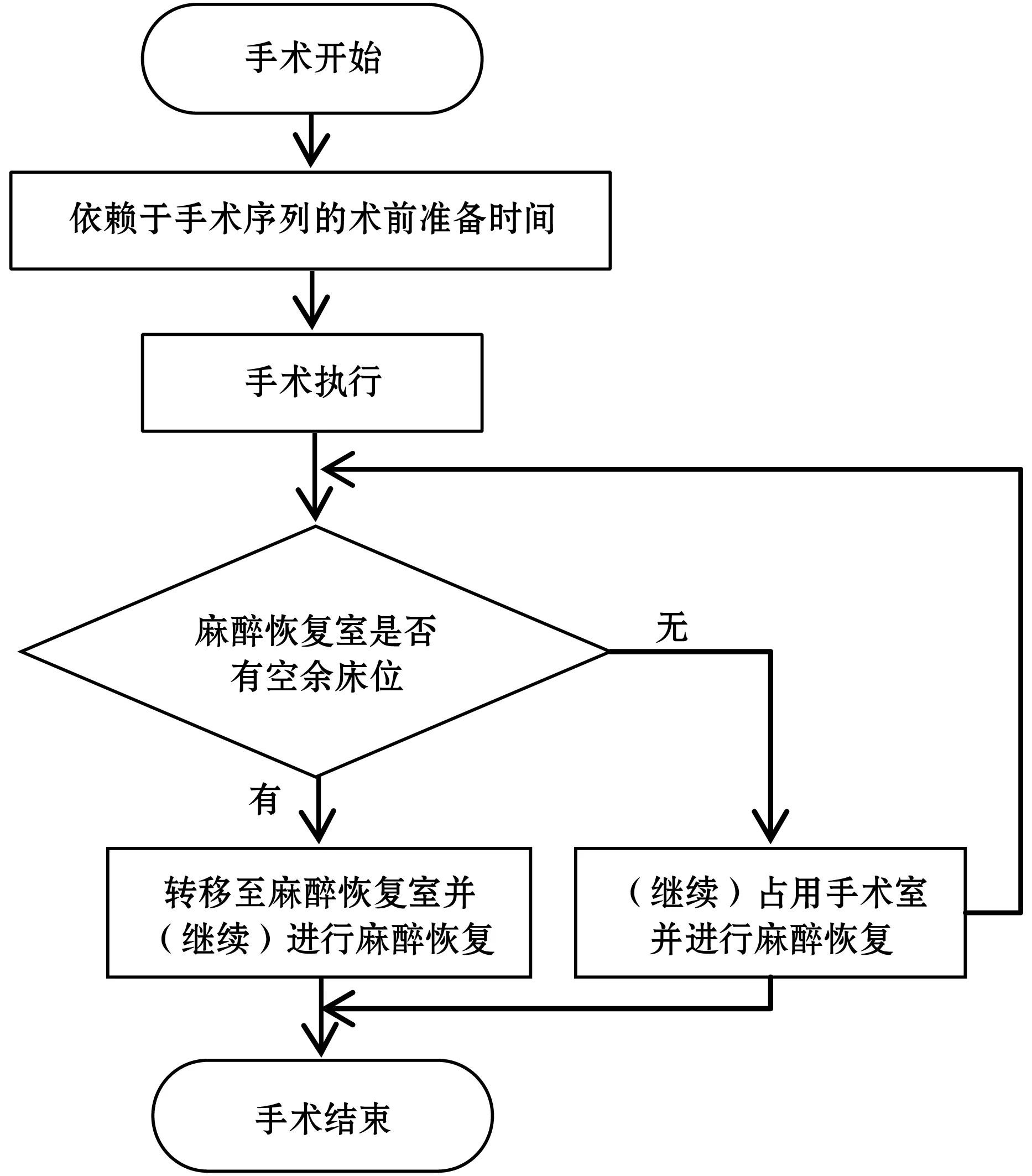
图1 每台手术的两阶段手术流程
1.2 问题假设
本文做如下假设:
(1) 在择期手术中,不考虑耗时过长的科室联合大型手术。
(2) 手术一旦开始,就不再中断。
(3) 待排手术的手术时长和麻醉恢复时长是通过经验丰富的医生和护士长的判断预先确定的,在排程中不考虑现实手术过程和麻醉恢复过程中的不可控因素。
(4) 对手术时长的预估已将术后清洁时间包括在内,且术前准备时间根据医院历史数据,假设两台接台手术为同类型时,准备时间为15 min,否则为30 min。
(5) 手术所需的所有医护人员和器械资源都是充足的并且能够准时到位,同时病人也具备能够按时进行手术的条件。
(6) 每个手术室排成日内的第一台手术的术前准备时间不予考虑。
其中假设(1)避免了大型手术可能会占用手术室时间过长,导致该手术室无法安排其他手术。
2 约束规划排程模型
2.1 约束规划与模型特征
约束规划是专门用来解决实际优化调度和规划中的有限域约束问题,它是人工智能的重要组成部分。约束规划算法综合了人工智能中一致性算法和启发式搜索算法,将求解问题的重点由算法的设计与实现转向对问题的模型建立,并采用约束推理方法,很好地解决了约束条件多,搜索时间长的问题。
本文所建立的CP模型是利用IBM ILOG CPLEX Optimization Studio 12.2平台中自带的OPL语言实现的。其优势在于OPL语言针对排程调度问题提出了区间变量和区间序列变量的概念,作为决策变量,区间变量表示一项任务或活动,具有起点、终点和过程长度等内在属性。在本文中,手术、手术室以及麻醉恢复床位均为区间变量,具有开始时间、结束时间和时长等属性。
2.2 模型构建
2.2.1 参数设定
Oi为所有已知待排手术,i=1…I;
Rj为所有开放的待排手术的手术室,j=1…J;
Ba为所有待安排术后患者的麻醉恢复床位,a=1…A;
Dk为所有待排手术的执刀医生,k=1…K;
Ti为手术i的手术过程持续时间,i=1…I;
ATi为手术i的患者麻醉恢复持续时间,i=1…I;
Pj为手术室j的正常开放时长,j=1…J;
S根据两台接台手术的不同类型所产生的术间准备时间集合;
Qulifiedi为可执行手术i的手术室集合,i=1…I;
ODi为每台手术i对应的执刀医生集合,i=1…I。
2.2.2 定义决策变量
定义区间变量如下:
①oi表示任务集合中在手术室执行的手术i。
在OPL语言中,该区间变量定义为:
dvar interval o[i in Oi] size T[i]
其中size定义了第i个区间变量的值。
②ani表示任务集合中在麻醉恢复室进行观察恢复的手术i。在OPL语言中,该区间变量定义为:
dvar interval o[i in Oi] size AT[i]
③roomj表示任务集合中待安排手术的手术室j。
④beda表示任务集合中待安排术后患者的麻醉恢复床位a。
⑤ORij为二维区间变量,表示任务执行手术i的手术室j的时间窗口。在OPL语言中,该二维区间变量定义为:
dvar interval OR[i in Oi][j in Rj] optional
其中optional表示该二维区间变量是一个可选择变量。
⑥OAia为二维区间变量,表示进行了手术i的患者进行术后观察的麻醉恢复床位的时间窗口。在OPL语言中,该而为变量定义为:
dvar interval OA[i in Oi][a in Ba] optional
定义区间序列变量如下:
⑦Qj表示手术室j中的手术进行顺序,在OPL语言中定义为:
dvar sequence Q[j in Rj] in all(i in Oi) OR[i][j]
⑧Aa表示麻醉恢复床位a上进行术后观察的手术患者的顺序,在OPL语言中定义为:
dvar sequence A[a in Ba] in all (i in Oi) OA[i][a]
2.2.3 约束条件
① 分配约束:
altervative(Oi,(ORi1,ORi2,…,ORij)) ∀i∈Oi,j∈Ri
(1)
altervative(Oi,(OAi1,OAi2,…,OAia)) ∀i∈Oi,a∈Ba
(2)
在OPL语言中利用alternative函数定义任务分配的唯一性,约束式(1)表示如果第i台手术oi出现在最终的排程调度中,那么执行手术i的j个手术室ORij中,只能有一个出现在最终排程结果中。同样,约束式(2)表示如果第i台手术Oi出现在最终的排程调度中,那么用来进行手术i术后观察的a个麻醉恢复床OAia中,也只能有一个出现在最终排程结果中。
由于手术室为有差别资源,因此约束式(3)表示手术oi只能在可接纳该手术类型的手术室roomj内执行。
(roomjnot inQualifiedi)⟹ORij≠j∀i∈Oi,j∈Ri
(3)
由于医生资源有限,因此存在一名医生需要执刀两台以上手术的情况。约束式(4)表示一名医生在同一时刻只能在一个手术室进行一台手术。
(ODi=ODu=k)⟹
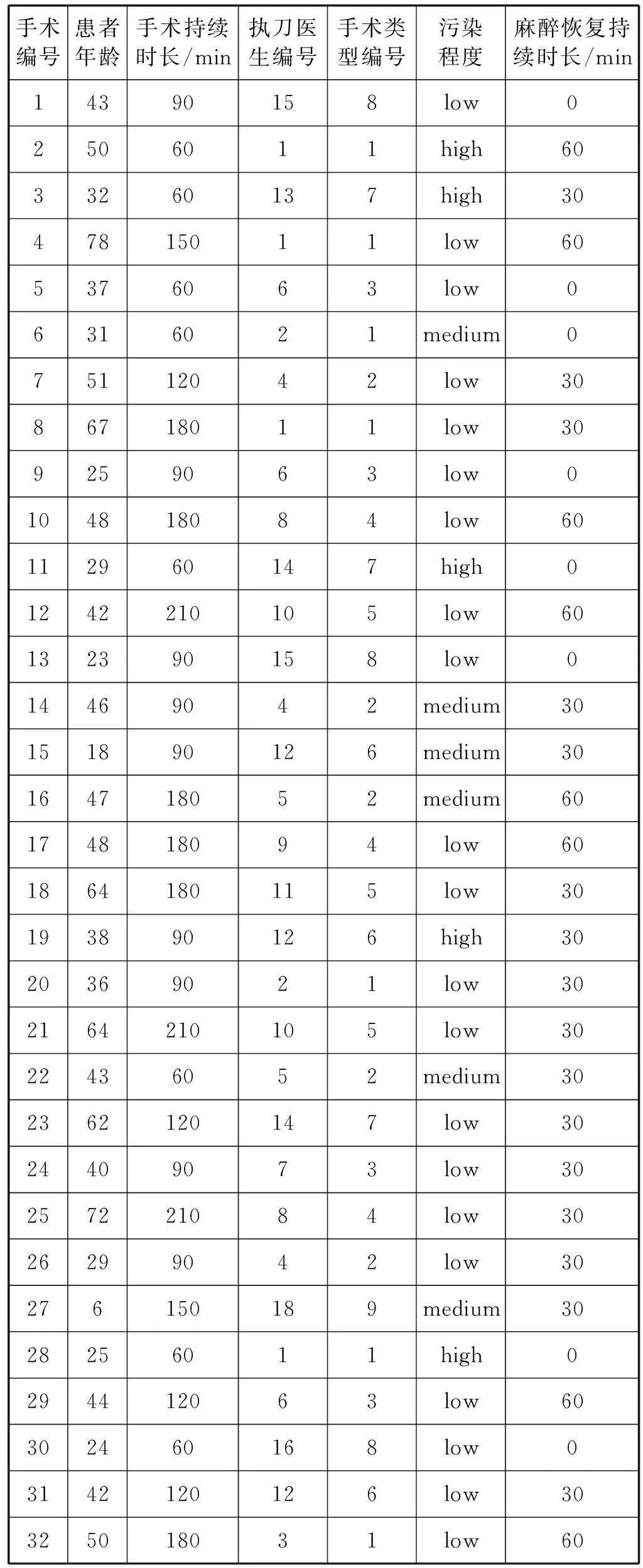
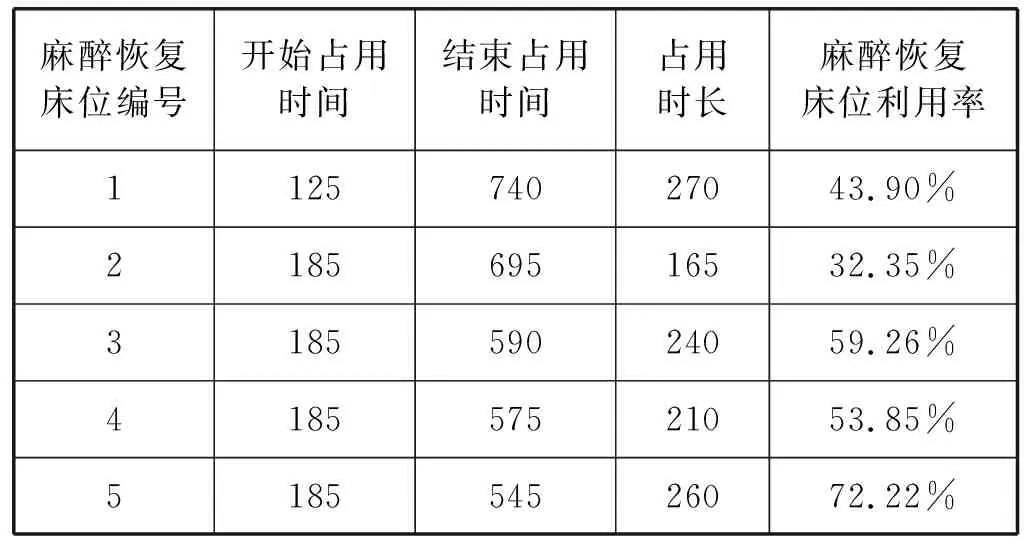
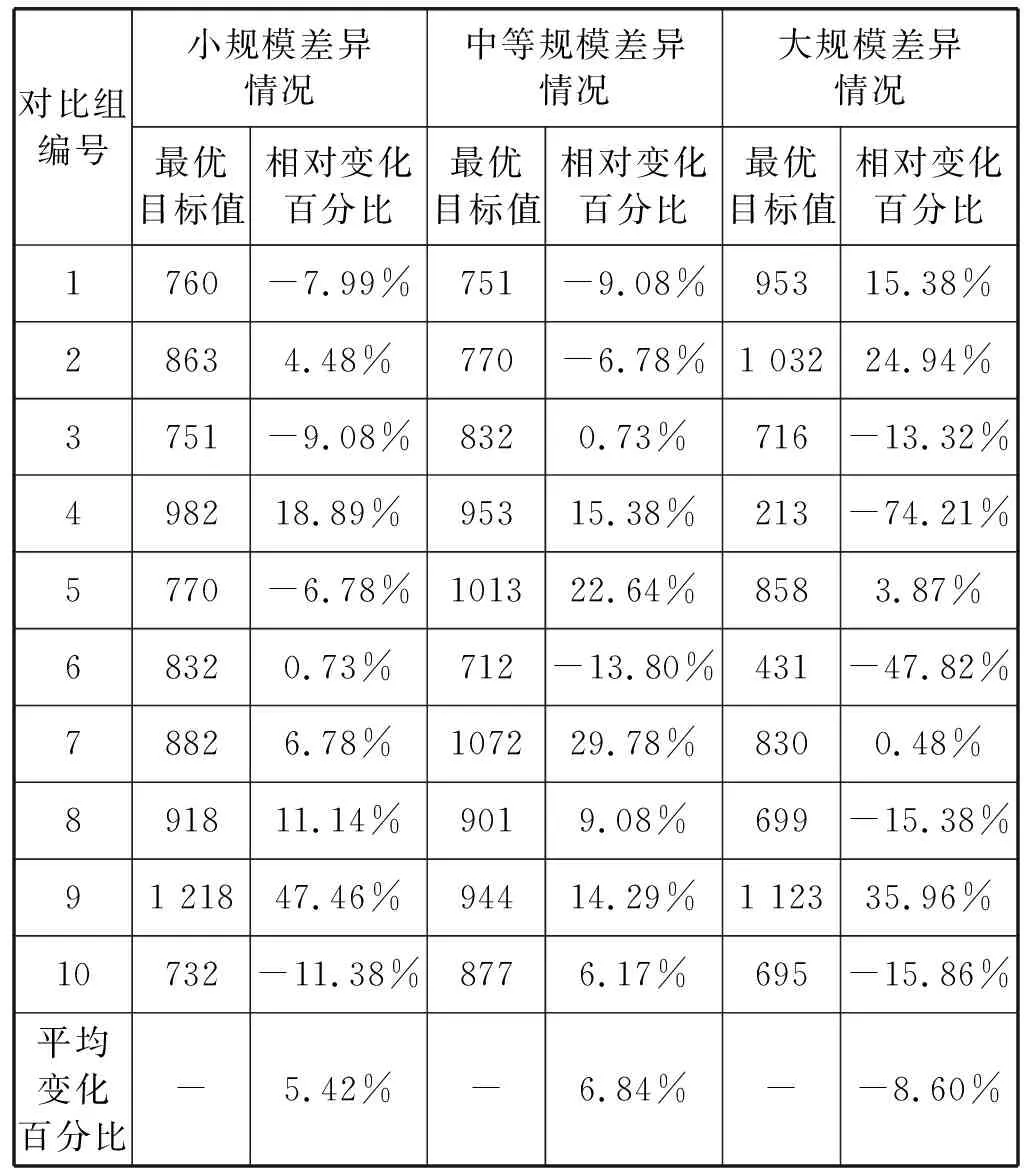
(endOf(oi) (endOf(Oi)>startOf(Ou)) ∀i,u∈Oii≠u,k∈Dk (4) ② 时间约束: span(roomj,(OR1j,OR2j,…,ORij)) ∀j∈Rj (5) span(beda,(OA1a,OA2a,…,OAia)) ∀a∈Ba (6) 约束式(5)、式(6)利用span函数确保手术室roomj的开放时间和麻醉恢复床beda的总利用时间覆盖所有被分配到该手术室执行的手术ORij和被分配到该麻醉恢复床的手术OAia的总持续时间。 约束式(7)、式(8)利用noOverlap函数确保区间序列变量Qj和Aa中的手术任务在时间上不重叠,且由于两台连续的手术因手术类型的不同存在时长不等的准备时间,因此在约束式(4)中,约束规划求解器会将相继的两台手术的类型与S集合中的元组匹配,从而得到相对应的准备时间。 noOverlap(Qj,S) ∀j∈Rj (7) noOverlap(Aa) ∀a∈Ba (8) ③ 顺序约束: endBeforeStart(ORij,ORuj) ∀i,u∈Oi且i≠u,j∈Rj (9) 每台手术都具有一定的优先级,约束式(9)利用endBeforeStart函数表示在分配到手术室roomj的若干台手术中,具有高优先级的手术需要在具有低优先级的手术开始之前完成。 在大型医院,患者从手术室转送到PACU进行术后观察的转移时间通常不超过5 min,因此约束式(10)表示手术ani的术后观察时间在手术oi执行结束后的第5 min时开始。 endBeforeStart(ORij,OAia,5) ∀i∈Oi,j∈Ri,a∈Ba (10) 2.2.4 目标函数 (11) 目标函数式(11)表示最小化所有手术室的超时占用时间。 为验证第2节提出的约束规划模型的有效性,选取某地方三甲医院的某日待排手术信息,模拟手术排程,确定最优的手术顺序。具体手术相关信息如表1所示。在手术排程日内,待排手术列表上共有40台手术,该医院共开放10间手术室,其中手术持续时长及麻醉恢复持续时长均为医护人员根据手术类型、患者身体情况等预估所得。表2 为该医院根据手术室配备的不同医疗器械等规定的每间手术室可接纳手术类型,如骨科手术只能在配备X光设备的手术室进行。 表1 待排手术相关信息表 续表1 表2 待排手术室可执行手术类型 本节报告数值实验结果,将约束规划模型用IBM ILOG CPLEXOptimizationStudio 12.2中的OPL语言实现,并用CP求解器求解。测试硬件平台为Intel Corei3-2370M,2.40 GHz CPU,4 GB内存。通过改变默认参数设置及搜索策略,提高CP求解器的求解效率,ILOG OPL语言提供了丰富的变量启发式及值启发式搜索策略,包括搜索阶段的设定、变量或值的选择器等。其中,搜索阶段可以令CP求解器优先搜索某一区间变量。我们在CP求解器中尝试了几种不同的搜索次序,最终发现先固定operation区间变量数组,再固定room区间变量数组,能够有效地提升CP求解器的求解效率。搜索阶段在用OPL定义如下: cp.setSearchPhases (f.searchPhase(o),f.searchPhase(room)) 所有手术室正常开放时间均为8小时,以8点作为0时刻,16点作为480时刻,超过480时刻的使用时间均算作超时占用。在允许最大失败100 000次的条件下,编程求解后得到最优解。对应目标函数最小值为826,CP求解器求解速度如图2所示。可见CP求解器收敛速度快,在求解大规模排程问题时,能够在较短的时间内求得问题的最优解。除6号手术室外,其余9间手术室存在超时占用时间,在最优解的情况下,手术与手术室和手术与麻醉恢复床位排程方案的甘特图如图3和图4所示。其中图3中斜线图案填充部分表示由于没有空闲的麻醉恢复床位,第15台和第33台手术只能分别在手术室占用15 min和30 min来进行术后观察,待有空余床位或麻醉结束后再移送麻醉恢复室或结束麻醉恢复。在寻求得到的排程方案下,麻醉恢复床位利用率如表3所示。 图2 CP求解器求解速度 图3 手术室排程方案甘特图 图4 麻醉恢复室排程方案甘特图 麻醉恢复床位编号开始占用时间结束占用时间占用时长麻醉恢复床位利用率112574027043.90%218569516532.35%318559024059.26%418557521053.85%518554526072.22% 表4 不同规模差异情况下最优目标值对比 手术室的成本对于医院的运营起着至关重要的作用。本文以最小化手术室超时占用时间为目标,降本升效,充分考虑手术的术中和术后两个阶段,以及手术优先级、依赖于手术序列的术间准备时间、医生资源的有限性和手术室资源的差异性,建立了约束规划排程模型。利用CPLEX的CP求解器对模型进行求解,通过对算例的求解分析,验证了约束规划模型对于解决排程问题的可行性与高效性。但是在现实医院的手术排程过程中,存在着更多的潜在约束条件和诸多不确定性因素,因此,日后可就此做更深入的研究。3 算例分析
3.1 算例数据


3.2 运算结果



3.3 对比分析

4 结 语

