基于EEMD-ARIMA模型的地区月负荷量预测

郭建鹏， 佘颖铃， 温步瀛

(1. 国网福建综合能源服务有限公司，福建 福州 350007； 2. 福州大学电气工程与自动化学院，福建 福州 350100)

0 引言

合理的预测是正确决策的基础和保证。负荷预测就是在考虑电力系统、气候、经济等各种因素的前提之下，通过对已有数据的挖掘和分析，对未来负荷量做出预先估计。负荷预测常运用于电网的规划、调度等问题，是其中不可或缺的一环[1]。

月度负荷预测可用于安排月度检修计划、水力调度计划、煤电计划等，是电力生产，检修，销售决策的重要依据。企业可以通过合理安排发电计划来降低生产成本、提高供电可靠性[2]。国内外关于负荷预测的方法有回归分析法[3]、灰色预测法[4]、模糊预测法[5]、时间序列法[6]、专家预测法[7]、神经网络法[8-9]等。文献[10]通过最小二乘法建立中长期负荷预测模型，其原理简单，但是对以往数据要求严格，影响因素的选取存在一定难度。文献[11]利用层次分析法结合专家经验，对城市化要素主观赋权，采用模糊聚类分析预测多因素影响下的中长期负荷。文献[12]使用灰色模型增加变权缓冲算子，并通过灰色关联分析和粒子群算法来确定模型的最佳参数。灰色预测要求历史数据呈指数变化趋势，数据灰度越大，预测精度越低。文献[9]分析了影响负荷模型的因素，采用人工神经网络对负荷模型参数进行预测，人工神经网络具有很好的自适应能力，但存在学习速度慢和局部极小点等问题。

在电力系统负荷预测中，时间序列法使用较为广泛，这类方法仅根据以往负荷数据建立随时间变化的数学模型，具有所需数据量少、工作量小、计算速度快等优点，对于平稳序列的预测精度高，对于非平稳序列则需要进行平稳化处理。文献[13]采用季节差分方法对数列进行平稳化；文献[14]根据月售电量的规律，利用X12季节调整法将月售电量分解为趋势量、季节周期量和随机量3个分量，从而提高预测量的稳定性；文献[15]利用小波分解将负荷分解为季节性需求负荷、需求响应信号及各种气象因素作用的负荷，然后利用自回归积分滑动平均(auto regressive integrated moving average, ARIMA)模型对季节性需求负荷进行预测，用支持向量回归模型对需求响应信号及受气象因素影响的负荷进行预测；文献[16]根据协整理论建立电力负荷序列与输入“温度”序列之间的ARIMAX模型，其信息量比经典自回归积分滑动平均(auto regres-sive moving aver-age, ARMA)模型的信息量小，拟合结果更精确；文献[17]考虑离群值对月度负荷的影响，建立计及离群值影响的季节性ARIMA月度负荷预测模型(regARIMA)，预测精度比普通ARIMA模型有所提高。

本文应用集合经验模态分解(ensemble empiri-cal mode decomposition ,EEMD)将负荷序列分解成若干分量，使得各分量平稳化，再通过ARIMA模型对各分量进行预测，基于某地区的月负荷量数据进行算例分析，结果表明经过EEMD分解后的预测值相比于未经过分解的预测值精度更高，误差更小，表明了EEMD-ARIMA模型在月负荷量预测中的实用性。

1 EEMD算法基本理论

1.1 EMD算法

经验模态分解(empirical mode decomposition, EMD)最早由美国科学家黄愕提出，能够将非平稳、非线性的时间序列信号自适应分解为若干个单分量信号[18]。EMD不需要同小波分析一样预先选定小波基函数，其基本思想是根据信号的局部时变特性，将原始信号筛分为若干个本征模态函数(intrinsic mode function, IMF)，各IMF分量都应满足2个条件：

(1) 任意IMF分量的极点和零点数量之差不大于1；

(2) 任意IMF的局部极大值和局部极小值的包络线之和的均值为0。

EMD的基本理论就是将频率混合的时间序列分解为频率规律的IMF分量和残余分量(residual component，RES)，过程如下：

(1) 找到时间序列x(t)的所有局部极大值点和极小值点，利用三次样条函数对原信号所有极大值点和极小值点分别进行拟合，构成原信号的上下包络线；

(2) 将上下包络线形成的时间序列相加，并求取其平均值a1(t)，将原信号序列与a1(t)相减得到新的信号序列h1，1(t)，即：

h1，1(t)=x(t)-a1(t)

(1)

(3) 判别h1，1(t)是否满足IMF的2个条件，如果满足，则h1，1(t)为EMD分解的第一阶IMF分量；若h1，1(t)不满足IMF条件，则将h1，1(t)定义为原信号序列，重复步骤(1)—(2)直到前提满足，此时得到的信号序列为第1个IMF分量，记为c1(t);

(4) 将原信号序列x(t)减去c1(t)得到r1(t)：

r1(t)=x(t)-c1(t)

(2)

(5) 将r1(t)作为下一个要分解的原信号，重复(1)—(4)步骤n次，直到残余分量rn(t)小于预设值，或为单调函数、常数，分解完毕，最终x(t)可以表示为：

(3)

事实上IMF的上下包络线很难始终为0，因此采用2个连续结果的标准差作为筛分终止判据：

(4)

一般SD的取值在0.2～0.3之间，本文SD取0.3。

直接对原始序列进行EMD分解，容易在序列两端产生发散，为了避免端点问题导致的模型失真，这里采用镜像拟合算法。

1.2 EEMD算法

当原始信号中掺杂幅值较小的间断性噪声时，EMD分解会产生模态混叠问题，这会使得IMF分量平稳性较差，为了改善这种情况，出现了通过噪声辅助的EEMD算法[19]。

EEMD算法的核心就是将高斯白噪声加入待分解序列，从而改变原序列的极值点分布，解决模态混叠问题。由于加入的白噪声会对原信号的分解结果产生一些影响，因此利用多重白噪声求均值为零的特性，将加入白噪声扰动后的原始分量分解得到的IMF分量分别求其平均值来控制噪声对分解结果的影响。其具体分解步骤如下：

(1) 初始化添加白噪声的次数(即试验总次数)Ne和幅值系数ε；

(2) 在原序列中加入随机高斯白噪声序列，其中Sj(t)是第j次加入的白噪声序列，xj(t)是染噪信号：

xj(t)=x(t)+εsj(t)

(5)

(3) 对染噪信号xj(t)进行EMD分解，得到i个IMF分量cij(t)和剩余分量rj(t)；

(4) 重复步骤(2)—(3)Ne次；

(5) 对Ne次重复操作后的信号进行EMD分解，对得到的IMF分量和剩余分量分别求均值：

(6)

(7)

(6) 最终x(t)的分解结果为：

(8)

2 ARIMA模型

ARIMA模型是由Box和Jenkins于1970年提出的一种时间序列分析方法[20-21]，在平稳序列预测方面应用较多。

ARIMA模型可以表示为ARIMA(p,q,d)。其中，d为对非平稳时间序列Y(t)差分的次数，d次差分后得到平稳序列X(t)；p为自回归阶数；q为滑动平均阶数。

差分得到的X(t)可以用自回归移动平均模型ARMA(p,q)来拟合，即：

Xt=c+φ1Xt-1+φ2Xt-2+…+φpXt-p+εt+θ1εt-1+θ2εt-2+…+θqεt-q

(9)

式中，前半部分为自回归过程，c为常量，φ1，φ2，…，φp为自回归系数；后半部分为滑动平均过程，θ1，θ2，…，θq为移动平均系数，εt为未检测的白噪声序列。

当q=0时，该模型为自回归模型AR(p)，式(9)可表达为：

Xt=c+φ1Xt-1+φ2Xt-2+…+φpXt-p+εt

(10)

当p=0时，该模型为滑动平均模型MA(q)，式(9)可表达为：

Xt=c+εt+θ1εt-1+θ2εt-2+…+θqεt-q

(11)

其具体流程如图1所示。

图1 ARIMA模型建模流程Fig.1 ARIMA modeling process

ARIMA模型预测的基本思路是：先建立预测值的时间序列，对其进行差分平稳化，通过自相关系数和偏自相关系数来确定模型阶数，然后进行参数的估计和检验，最后用参数合适的模型对预测量进行预测。

3 基于EEMD-ARIMA模型的月度负荷预测

3.1 EEMD-ARIMA模型

受经济、气候等因素影响，月负荷量是非平稳序列，所以要先对其进行平稳化。因此，本文建立基于EEMD分解的月度负荷量预测模型，以下简称EMD-ARIMA预测模型。具体步骤如下：

(1) 对月负荷量进行EEMD分解，将其分解为不同时间尺度的分量；

(2) 对各分量分别进行ARIMA模型预测；

(3) 将各分量预测值相加，从而得到最终的月负荷量预测值。

3.2 评价指标

为了评价不同的模型对预测结果的影响，本文从准确度和相似度2个方面对模型进行评价。

(1) 准确度。在数值方面，本文使用了归一化绝对误差EAE和归一化均方根误差ERMSE来对模型进行衡量：

(12)

(13)

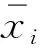
(2) 相似度。在负荷曲线变化方面，本文用如下指标[18]：

(14)

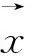
4 算例分析

4.1 实验数据

为了验证模型的可靠性与预测精度，本文基于某市2010年1月到2016年7月共79个月的负荷量数据来预测2016年8月到2017年7月12个月份的负荷量。

4.2 月售电量预测及结果分析

本文应用Matlab软件对月负荷量进行预测，先对原始序列进行ADF单位根检验，Tau统计量的P值为0.767 3，远大于0.05，说明原序列是非平稳序列。对负荷量进行EEMD自适应分解(取Ne为100，ε为0.1)，根据信号的局部时变特性将负荷量进行筛分，得到5个IMF分量和1个RES分量，各分量具有不同的时间尺度，其中IMF1和IMF2不具有规律性，为随机分量，IMF3和IMF4为负荷量中的周期分量，而IMF5和RES分量为负荷量中的趋势分量。其分量如图2所示。

图2 月负荷量的EEMD分解结果Fig.2 EEMD decomposition results of monthly load

对各分量进行平稳性检验，若不平稳则进行差分平稳化，观察各分量的自相关系数和偏自相关系数，初步确定p和q的取值范围为[0,10]，选取置信水平为95%，通过信息最小准则(Akaike′s informa-tion creterion, AIC)确定具体参数如表1。

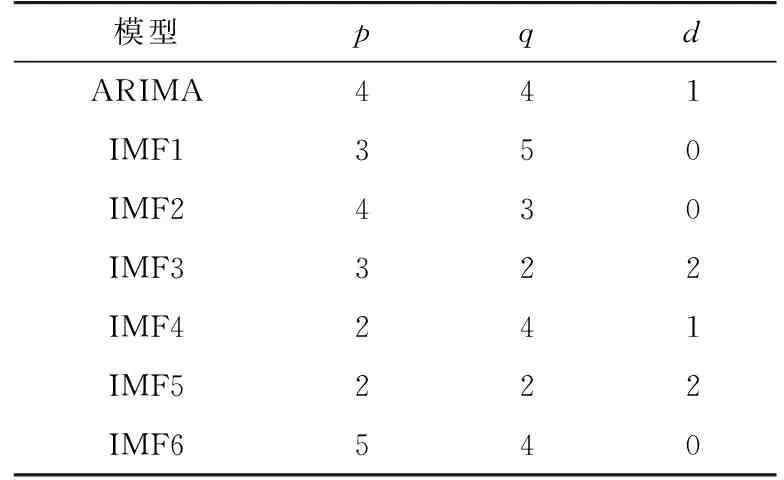
表1 模型参数的选取Tab.1 Selection of model parameters

负荷实际值、反向后传(back propagation,BP)神经网络预测值、ARIMA模型预测值以及EEMD-ARIMA模型的预测值结果如图3所示。

图3 月负荷量预测结果Fig.3 Monthly load forecast results

3种模型预测结果的准确度和相似度数值如表2所示。在数值方面，不论是绝对误差还是均方根误差，本文模型的预测值误差都小于其他2种模型，在4%以内。而相似度方面，本文模型的相似度为0.999 2，比ARIMA模型的相似度更高，与实际负荷变化趋势更相似。从数值和相似度2个方面，都可以看出EEMD-ARIMA模型的优势，经过EEMD分解后，其分量比原始序列平稳，而ARIMA模型对平稳性好的信号序列预测精度高，采用EEMD-ARIMA模型预测可有效降低误差，提高预测精度。

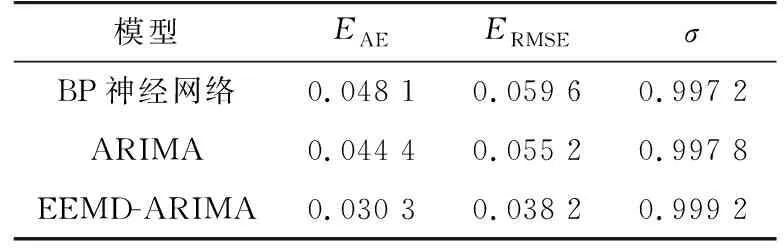
表2 各类模型的性能比较Tab.2 Comparison of models

5 结语

考虑到负荷量受气候、经济等因素影响及平稳性较差的问题，普通ARIMA模型难以取得较高精度，因此本文采用EEMD分解，用于原始数据，得到有限个更为平稳的分量，对各分量分别建立ARIMA预测模型。经实验对比，针对地区月负荷量预测，不管在数值方面还是相似度方面，EEMD-ARIMA预测模型都优于ARIMA模型。