两种VIENNA整流器控制策略比较
杨佳, 曼苏乐, 杨晨
(1.上海交通大学 电气工程系 ,上海 200030;2.国网苏州供电公司,江苏 苏州 215008)
0 引 言
VIENNA整流器具有功率密度高,开关损失小,体积小等优点,是一种基于三相三电平拓扑结构的整流器。近年来也成为了电力电子学术界和工业界的重要研究对象。因而VIENNA整流器相关领域有大量的控制策略得以应用,例如空间电压矢量控制、直接电流控制等。本文搭建了VIENNA整流器试验平台,并对基于电压定向SVPWM控制和基于物理解耦的单周期策略两种控制策略进行了仿真分析和试验分析。
1 VIENNA整流器的控制原理
1.1 VIENNA整流器的数学模型
如图1所示,VIENNA整流器由3个独立的桥臂组成,而每个桥臂由2个功率二极管和一个可控双向开关组成,而该可控双向开关由两个N道沟增强型MOSFET组成[1]。图1中Sa、Sb、Sc等双向开关皆由如上所示两个MOSFET构成。
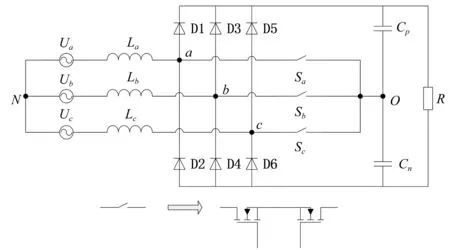
图1 VIENNA整流器拓扑结构
由图1可知,VIENNA整流器的电压方程为:
(1)
式中:Ua、Ub、Uc为三相输入电压;La、Lb、Lc为三相各输入电感;UON为输出电压中点到三相输入中性点的电压;UaO、UaO、UaO为整流器各相的输入电压。
对于三相对称系统而言,当输出测电容电压平衡时,UCp=UCn=Udc/2,由此可知
(2)
式中:UON为输出电压中点到三相输入中性点的电压;UaO、UaO、UaO为整流器各相的输入电压。
1.2 SVPWM控制策略工作原理
SVPWM控制策略工作原理如下:就桥臂D1-D2而言,当开关Sa开通时,整流器的输入端电压钳于输出侧电压中点;当开关Sa关断时,整流器的输入端电压为+Udp(正半周电容电压)或-Udn(负半周电容电压),输入电压极性与输入电流方向正负半周相关。根据以上原理,桥臂D1-D2有“1”,“0”,“-1”等3个开关状态,即整流器的输入端被分别钳位于输出侧电压的正极、中点和负极。同样,可以根据此分析方法对B、C两相进行相同分析[2]。
整流器由3个桥臂组成,而每个桥臂可以有3个开关状态,但由于VIENNA整流器结构的特点,[1 1 1] 和[-1 -1 -1]这两个开关状态并不存在,因此总的开关状态数为33- 2 = 25,这25个开关状态一共产生了19个不同的电压矢量,开关状态及空间矢量如图2所示。
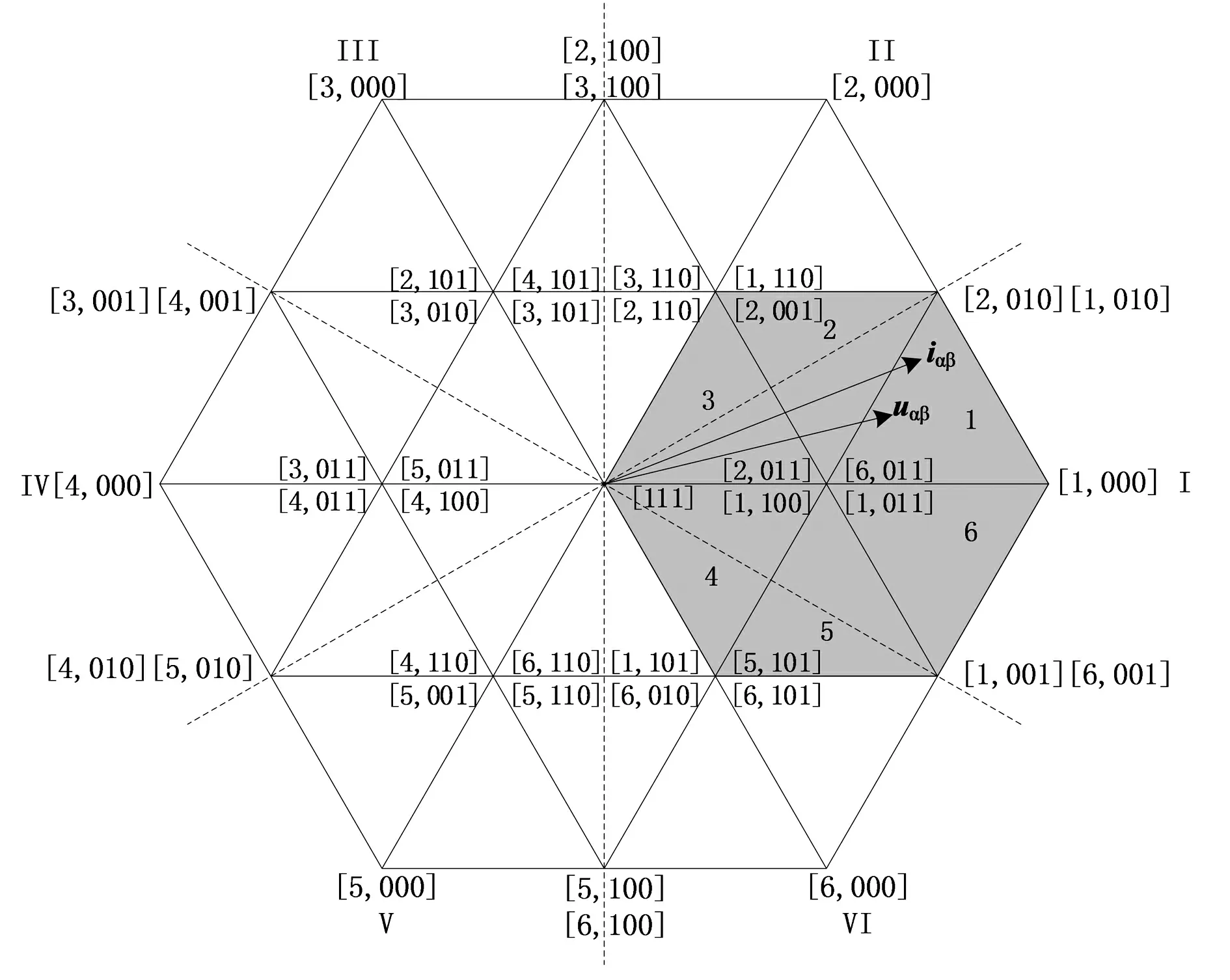
图2 VIENNA整流器的空间矢量图
SVPWM控制策略有其固有的控制要求,在电压的调制过程中,必须保证电压矢量与电流矢量同极性。在控制过程中,根据电流极性的不同,将整个空间矢量平面划分为6个电流扇区,划分方法如图2所示,并依次命名为电流扇区(SI)I,II,III,IV,V,VI。同样,将对应电流扇区根据电压矢量调制的需求划分为6个小扇区,依次命名为电压扇区(SV)1,2,3,4,5,6。
SVPWM控制策略中的矢量调制采用的是常用的7段脉冲法。根据电压矢量的电流扇区和小扇区位置,选择合适的空间矢量调制对应SVPWM脉冲波形。根据伏秒平衡原理,可以得到矢量作用时间方程如下:
(3)
式中:V0、V1、V2为根据电压矢量所在扇区划分选择的小矢量、大矢量、中矢量;Ts为控制开关周期,T0、T1、T2分别为小矢量、大矢量、中矢量作用时间。根据式(3)可以解得各矢量作用,从而得到对应SVPWM波形。
以图2所示电压矢量为例,电压矢量uαβ位于电流扇区的第I扇区,同时位于该电流扇区的第1电压扇区(即电流扇区SI=I,电压扇区SV=1)时,开关控制脉冲序列为100-000-010-011-010-000-100,其中小矢量作用时间为T0,大矢量作用时间为T1,中矢量作用时间为T2,其对应的SVPWM波形如图3所示。
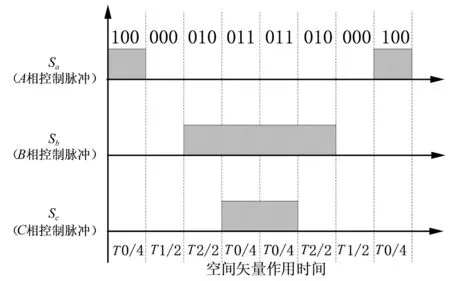
图3 SVPWM三相脉冲波形
1.3 物理解耦的单周期控制方案
对三相三线制VIENNA整流器进行解耦有一个重要的前提,解耦的系统必须是三相对称系统,如果三相偏差过大,则电流环需要保证三相功率平衡,才能实现解耦[3]。在满足系统对称性的前提下,可以将三相三线VIENNA整流器解耦,可等效为三个单相三电平整流器的并联。其中单个单相三电平整流器的结构如图4所示(以A相为例)[4]。
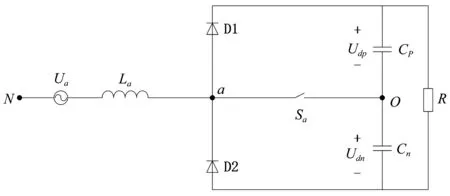
图4 单相三电平整流器主电路(A相)
为了简化推导过程,分析稳态特性,先作以下假定:
(1)忽略电感中的电流纹波,电路处于准稳态,且运行与CCM模式;
(2)输入电压频率远小于开关频率,输入电压ua、电感电流ia、电容电压Udp、Udn在一个开关周期内可以认为是恒定值;
(3)电路中各元件设定为理想元件。
基于以上假定,使用状态平均法[5]6-15可得到电感的平均状态方程。以A相为例,所得平均状态方程
(4)
式中:符号ia为A相电感电流的开关周期平均值;Ua为A相输入电压的开关周期平均值;Udp为正向电容电压Udp的开关周期平均值;Udn为负向电容电压Udn的开关周期平均值;UON为输出电压中点到三相输入中性点的电压的开关周期平均值;La为A相输入电容;d为占空比。如果将输入电压和电感电流都取绝对值,则整流器在正、负两半周内方程相同,故只对正半周进行分析。
使用扰动法以及线性化[5]15-18,可得电路的静态工作点方程以及线性化之后的小信号交流模型。
Ua-UON=(1-D)Udp
(5)
(6)
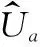
由以上方程可得到电感电流对占空比的传递函数
(7)
式中:Udp为正向电容Cp上的电压;La为A相输入电容;ia为A相输入电流。
2 仿真分析
为了对以上两种控制策略进行比较分析,在Simulink仿真环境下建立了仿真电路,具体仿真参数为:三相3线制输入110 V/50 Hz,输出端DC 400 V;开关频率f=12.8 kHz,输出最大功率Pmax=1.5 kW,三相输入电感L=400 μH,输出侧两滤波电容Cp=Cn=440 μF。
图5给出了两种控制策略下VIENNA整流器的输入电压、输入电流波形。仿真系统中测得SVPWM控制策略的输入电流的THD=8.31%,单周期控制策略的输入电流的THD=10.77%。
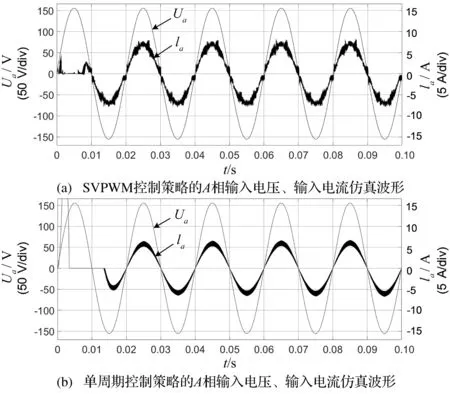
图5 两种控制策略下的整流器A相输入电压、输入电流仿真波形
3 试验分析
为了对两种控制策略仿真结果进行比较验证,采用DSP芯片tms320f28346制作了一台三相3线制VIENNA整流器试验样机,进行试验对比。
试验样机参数为:电源线电压Un=110 V,直流母线电压Udc=220 V,输入侧相电感La=0.4 mH,直流母线电容Cp=Cn=440 μF,最大输出功率Pmax=1.5 kW。
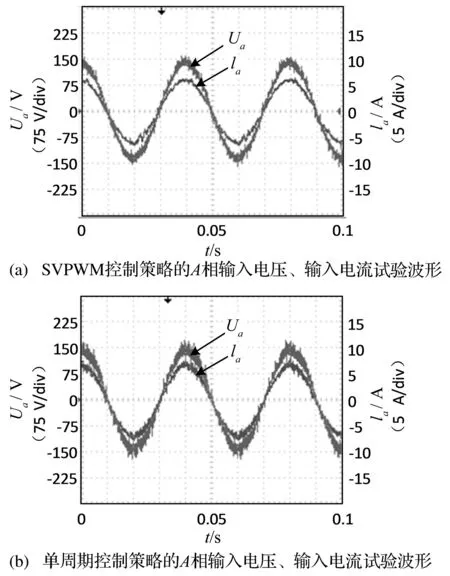
图6 两种控制策略下的整流器A相输入电压、输入电流试验波形
SVPWM控制策略和单周期控制策略的输入电压、输入电流试验的波形分别如图6所示。而两种控制策略对应的输入电流波形谐波如图7所示,SVPWM控制策略的输入电流的THD=3.10%,单周期控制策略的输入电流的THD=3.05%。
从波形及THD分析中,可以得知SVPWM控制策略的谐波主要为低次谐波,而单周期控制策略的谐波中低次谐波分量低于SVPWM控制策略,主要集中于开关频率分段。因此,采用SVPWM控制策略相较于单周期控制策略,具有较小的开关损耗。

图7 两种控制策略下的整流器输入电流谐波分析
4 结束语
综上所述,在VIENNA整流器中,采用SVPWM控制策略与
单周期PFC控制策略都可以得到较小的THD,而采用SVPWM控制策略得到的输入电流波形具有更小的高次谐波分量,因而具有更小的开关损耗。从提高整流器的整体效率的角度考虑,SVPWM控制策略是一种更为理想的控制方法。

