基于时序模拟方法的电力系统运行可靠性分析

田德春，张 菁，李天浩，朱时雨

(1.国网锦州供电公司，辽宁 锦州 121004；2.国家电网公司东北分部，辽宁 沈阳 110180)

电力系统的可靠性研究一直是一个至关重要的课题。即使在自然灾害发生的情况下，许多国家也对其可靠性指标进行了更严格的限制，以达到更高的安全水平。然而可靠性改进会增加额外的成本，因此要有效地控制利益/成本比。通过平衡可靠性收益(通常以未提供需求的预期成本的节省量)与所需的运营成本和投资的平衡来提高可靠性的最佳水平，以提高可靠性[1]。

为研究电力系统中电网故障诊断，文献[2]引入知识表示的方法将故障信息进行转化，构建了基于知识表示的电网故障诊断策略。其他学者对蒙特卡罗模拟在电力系统中的应用做了大量研究，文献[2]在主动管理(AM)模式下，提出了一种考虑主动配电网转供能力的可再生电源(RES)优化配置模型。文献[3]建立主动配电网中不确定性因素的模型，采用拟蒙特卡罗(QMC)模拟法抽取Sobol确定性低偏差点列，以随机潮流计算为工具，对主动配电网的节点电压越限情况进行模拟。文献[4]为了提高微电网随机潮流计算的精度，提出了将蒙特卡罗抽样和半不变量法相结合的方法。文献[5]研究了基于模拟法的概率静态电压稳定评估方法，通过引入拟蒙特卡罗模拟获得输入随机变量样本。基于非序贯蒙特卡罗方法模拟电网的运行模式，在此基础上进行潮流计算和输电元件负载率计算，得到系统的关键元件集[6]。利用蒙特卡罗抽样仿真法，文献[7]提出适应于含间歇性分布式电源的概率潮流求解方法。文献[8]开发了一个框架，通过使用负载控制为不同的消费者提供不同的可靠性水平，该方法可以支持改进可靠性，推迟新投资，甚至在某些情况下可以消除对额外基础设施的需求[9]。特定网络投资(即新线路或变压器)的可靠性影响可以通过仿真技术来确定[10]，采用数学模型来找出精确的数学解，基于蒙特卡罗模拟来表示电力系统中偶然性的随机性质。

本文通过模拟优化(optimization via simulation,OvS)提出一种基于可靠性改进来确定新网络投资的方法。采用工业COMPASS算法来找到新的网络资产组合，从而提高系统可靠性，同时考虑电力系统运行的详细描述，包括蒙特卡罗顺序模拟(Sequential Monte Carlo Simulations,SMCs)的故障建模，以及组件与恢复时间之间的时间依赖性的详细模拟。OvS根据在多种场景/故障下系统的预期性能，找出优化问题的最佳解决方案。

1 蒙特卡罗算法分析

1.1 蒙特卡罗时序模拟

为实现在给定范围(1天)内进行准确的可靠性分析，首先确定调度操作，当每个生成单元的开/关状态为固定时，通过DC-OPF问题模拟实时操作。预期的未供电能量将取决于系统基础设施和操作功能，例如预定的储备量、发电机组的斜坡率限制、启动时间等。

在24 h内确定小时生成调度计划，其中总体运营成本最小化。文献[11]中对混合整数线性规划公式进行推导，考虑了具有容量限制的多母线网络。每个单元都通过使用可变成本、启动成本、关闭成本、最小稳定发电、最大功率输出、斜坡率限制(上下)、最小停机时间和最小正常运行时间来建模。

应用直流最优潮流(DC optimal power flow,DC-OPF)来确定发电机组故障发生后重新分配的电力系统的实时运行方式。该线性编程问题可确定每个时段每个单位的生产量，以最小的成本满足供应和需求。成本函数是最小化总生产成本，包括每个母线处未提供的能源成本(energy not supplied,ENS)。如果发生停电，DC-OPF将提供一种使上述成本函数最小化的解决方案，输出每个单元的最佳生产和每个母线的ENS。

通过蒙特卡罗顺序模拟生成随机场景，对网络故障进行建模。设置每个传输线的故障率为λ和恢复时间为r(h)。

计算可靠性的完整算法流程如图1所示，1天计算1次，然后执行SMCN次(即模拟)。每个模拟从t开始(t= 1,2,3,…,T)，并且在每个t中迭代传输线/分支B的集合，其中bi表示分支i(i= 1,2,3,…,m)，将bi生成均匀随机值Z，如果Z小于故障率λ，则bi失效。更新参数TFi(分支i的故障持续时间)和bi状态。如果分支i离线，则更新参数TFi。以t中分支机构的在线/离线状态，作为初始条件。DC-OPF模块的输出对应于发电生产，t为ENS。重复此过程，直到t达到T(24 h)，完成1次模拟。当执行1天的N次模拟时，完成整个SMC。

图1 SMCs算法流程图

1.2 优化仿真

通过仿真优化(OvS)是指根据多个场景实现系统的预期性能(即平均指标)找到最佳解决方案(最大化或最小化)。OvS算法探索最有效的解决方案区域，同时利用某种形式的随机化来跳开局部最优区域。由于可行区域是整数值，所以使用离散OvS(DOvS)，该问题可以表述如下：

(1)

式中：Φ∩Zd是可以有界或无界的集合。

在该过程中，单个模拟的输出F(x,ξ)来自一个“黑箱”模型，其内部结构对解决方案仍然未知。一个具体的系统仿真x(其中x是表示一组线是否被构建的二进制向量)将返回不提供的能量F(·)，用于场景实现ξ(每天模拟1个潜在实现多重故障)。目标是尽可能减少不符合资源预算约束条件的预期能量，如式(2)所示：

(2)

(3)

0≤xi≤1,i=1,2,…,d

(4)

xi∈Zd,i=1,2,…，d

(5)

在图2中，十字架具有比定义主动约束更好的性能测量，右上角点位于一个非特征结构中，因为它的3个相邻中至少1个表现出更好的性能，并且在任何其它领域中没有定义主动约束。

图2 2个利基周围最明确的区域

2 案例分析

2.1 IEEE 14母线测试系统

a.故障条件下的系统运行

使用IEEE 14母线测试系统，其具有5个发生器，19个传输线/变压器和11个负载,对其进行蒙特卡罗模拟仿真，如图3所示。该系统进行了修改，以满足模拟要求：①为发电机组增加更多的技术/经济参数(如最小功率输出、斜坡速率限制、最小停机时间和运行时间以及生产、启动和停机成本)；②增加传输特性(有功功率容量)；③考虑负载分布。

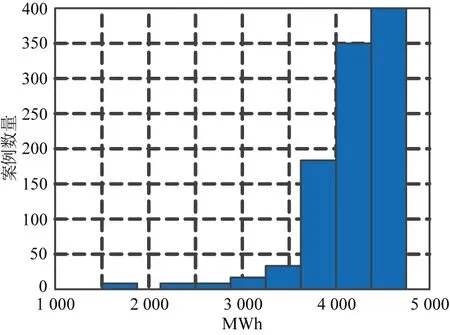
(a)ENS无线恢复

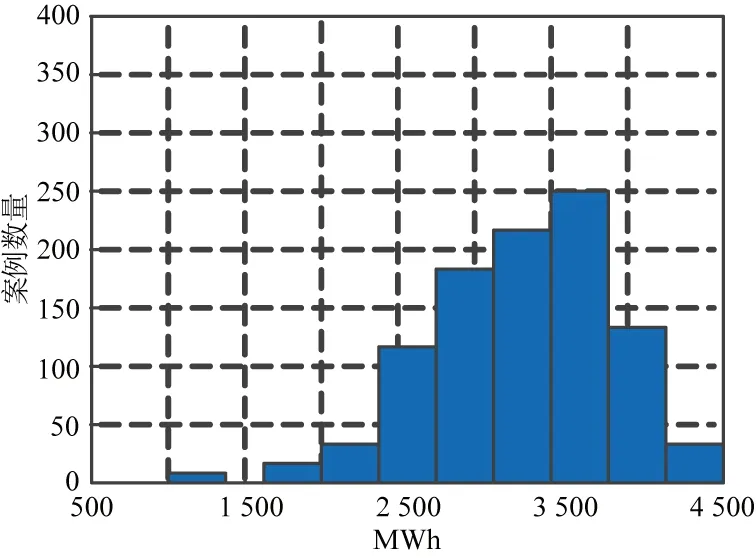
(b)4 h恢复时间图3 蒙特卡罗模拟仿真图

图4 恢复时间与EENS关系曲线

蒙特卡罗模拟方法有4个参数：网络/线路故障率λ(每小时发生)，恢复时间r(h)，蒙特卡罗运行次数N=1 000，每次运行时间间隔T=24 h。如果对于没有线路恢复的每条线路的故障率设置为0.05，期望的ENS为4 234.32 MWh/d。如果每行的恢复时间设置为4 h，则预期的ENS为3 143.59 MWh/d。在图4中给出了恢复时间与EENS关系曲线图。

b.系统投资及可靠性分析

基于可靠性评估运行ISC算法并确定最佳网络投资。二进制向量x∈{0,1}|A|代表决定安装候补线，其中:A={(i,j)∈V×V/E}，V是现有总线的集合;E是现有线路或分支的集合。考虑预算1和3条新线(即b=1和b=3)。对于b=1可能整数解的数量是72，|A|=72能够约在143 min内找到最佳解决方案。

表1和表2显示了假设恢复时间为2 h的案例研究结果。通过ISC获得的最佳解决方案需要1 581次评估才能通过测试。

另外，这种方法运行的预算为3行，其中可能的解决方案数量为1+71+71×70+71×70×69=347 942(所有可能的0,1,2和3行的组合)。结果总结在表3和表4中，其中表3包含3个潜在的解决方案，从统计学角度看，最佳解决方案无法被认可(1-aG=90%)。由表4表明，当预算等于3(在347 972个可行组合中)时，确定最佳解的模拟时间为141 min。

表1 14总线ISC结果-线1预算

表2 14总线的性能结果-线1预算

表3 14总线ISC结果-线3预算

表4 14总线的性能结果-线3预算

2.2 IEEE 57-母线测试系统

为测试所提方法的可扩展性，对IEEE 57-母线测试系统进行更多分析。 本文考虑了14母线情况下的同一组参数。

当恢复时间设置为3 h时，未提供的预期能量等于2 389.5 MWh/d。当认为发生故障后，中断线路不能恢复时，EENS将增加到5 151.08 MWh/d。与之前情况一样，确定了1条和3条新线路的预算解决方案。在这种情况下，问题有大约350万可能的解决方案(b=3)。容忍度和统计学意义的参数如前所述。表5—表8总结主要结果。

表5 57总线ISC结果-线1预算

表6 57总线性能结果-线1预算

表7 57总线ISC结果-线3预算

表8 57总线性能结果-线3预算

对于b=1，解决方案比14母线情况(表1和表5中的比较)呈现较少的评估；这是因为在优化过程中比较的是解决方案的性能。两种措施影响收敛的质量、方差和性能水平。这些措施在14母线情况下比在57母线情况下更大。值得注意的是，在表1中，方差系数大于表5。事实上，较低的方差系数产生更准确的估计，评估较少。当b=3时，可以观察到相同的特征，其中表3(14母线)中的方差系数大于表7中的方差系数。

此外，不可能直接比较每个案例研究中使用的评估次数。虽然在14母线网络中投入更大(即每个解决方案候选人对2个预算的评估次数，b=1和b=3)，但是在57母线示例中，因为数量增加，整个过程需要更长的时间。这可以通过比较b=1的表2和表6之间的模拟时间和评估次数以及b=3的表4和表8来观察。

表3(14母线和b=3)和表5(57母线和b=1)存在多个最优解；相反，表1(14-busbar和b=1)和表7(57 busbar和b=3)仅显示每种情况的一个最优解，因为在执行COMPASS阶段后，可以找到一个唯一的解决方案。

3 结论

通过仿真方法提出优化，以确定提高系统可靠性网络投资的最佳投资组合。该模型考虑了系统操作的详细说明，同时考虑到网络故障阵列的发生。提出的优化方法可以有效地计算解决方案，并对系统运行进行高度详细的建模，包括停机对整个时间内未提供的需求的影响(即恢复)。所提出的方法应用于IEEE 14总线和57总线系统，表明其能够在合理的时间尺度上找出良好的解决方案。