基于纵向超声导波的管道焊缝缺陷识别研究

王向宇，张伟伟，张 雷，钟江城

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；2.太原科技大学 应用科学学院，山西 太原 030024)

0 引 言

管道在服役过程中不可避免的会受到设计载荷、环境腐蚀或人为破坏等影响，从而导致管道破裂发生泄漏事故。2012年4月23日，新疆巴音郭楞蒙古自治州发生一起因为施工造成的天然气管道泄漏事故，事故造成附近3万多户居民和餐饮商户停止供气[1]，给生产和居民的生活带来诸多不便。数百公里的管道，特别是核电站(NPP)的弯头和焊接接头，易受老化和其他类型的损坏[2]。随着焊接结构不断向高参数、大型化、重型化发展，对焊接质量提出了越来越高的要求。在许多重要的焊接结构中，如锅炉、船舶、桥梁和高层建筑等，缺陷的存在都将影响焊缝处的质量，对焊接结构件的安全使用造成威胁。因此，管道焊缝缺陷检测对于管道的安全服役具有重要意义。

近些年，其他国家开发了相应超声类检测产品，比如：德国管道检测公司开发了专用于检测输油管道的超声裂缝检测器[3]；为解决超声波耦合问题，英国国家天然气公司提出了轮胎式换能器的设计思路[4]；美国一家公司研制出了相控阵超声波检测器[5]。但大多数超声检测技术均需要直接与焊缝接触，通过扫描焊缝区域来检测焊缝缺陷，对于穿墙的焊接管道或者人员不易接近的焊缝检测，传统超声波检测方法就必须先移除覆盖物或进行其它工序以满足测试要求，给测试造成成本高，且不能在线检测等问题[6]。超声导波检测技术是近几年非常流行的一种无损检测技术，它是在结构的一端激励超声导波，通过应力波在结构中的传播特性判别结构中的缺陷特点[7]。超声波检测适用于壁厚为5～50 mm，材质为低碳钢、低合金钢等金属材料的石油天然气长输、集输及其站场管道环向对接接头的超声波检测与质量分级[8]。

最近几年也有很多学者致力于超声导波在无损检测技术中的研究。他得安等分析了导波在管中的传播特性以及管材内径与壁厚之比变化时，对导波频散特性的影响[9]；王悦民等利用研制的磁致伸缩超声导波无损检测装置对长直无缝钢管、舰用锅炉U型管和弯管进行了大量试验研究[10]；刘胜等将磁致伸缩超声导波无损检测技术应用于长输管道的检测中，可以提高检测效率和检测灵敏度[11]；张伟伟等提出一种基于相关性分析的管道缺陷超声导波检测方法；M.J.S.Lowe介绍了导波传播及其对缺陷的敏感性的研究，建立了缺陷尺寸与波反射强度之间的关系[12]；H.Yun研究了基于双金属复合管中导波传播的损伤检测，可以识别轴向和圆周方向的损伤位置[13]；Z.Fan介绍了导波和焊缝缺陷之间的相互作用，讨论了2种导波对不同缺陷的敏感性，并得出了检测这些缺陷的适当导波频率[14]；G.Luo引入无缺陷弯曲管和缺陷弯管的FE(有限元)模型，分析了超声导波的能量分布，模态转换和缺陷检测[15]；许延春应用超声波检测技术测定岩体在不同裂隙宽度下的声波传播速度，进而推算岩体动弹性模量，并对比分析注浆前后裂隙岩体的损伤变量与动弹性模量的变化程度及规律[16]；W.Zhang提出了一种基于分析非线性振荡器与记录的纵向超声导波信号作为附加输入的响应检测技术，通过检测回波来检测小结构损伤。经过研究人员的不懈努力，关于导波的基本理论、数值计算与模拟和实验技术取得了长足的进步[17]。从以往的研究中可以看出，超声导波检测技术在无损检测中的应用非常有效，但这些研究都只是定性地检测缺陷程度和缺陷的位置，并没有得到缺陷的具体尺寸。

文中将利用数值模拟提出一种基于纵向超声导波检测焊缝缺陷的无损检测技术，首先利用ANSYS软件进行焊接管道焊缝缺陷的不同工况模拟，得到各个测点的位移时程曲线图；通过观察导波在焊缝缺陷前后的传播特征，以入射波与透射波峰值点之比作为损伤指标，检验损伤指标识别焊缝缺陷的位置与大小的能力。

1 数值模拟

1.1 模型建立

管道的几何模型以及焊缝处的截面[18]，如图1所示，管道长2.6 m，外径76 mm，管壁厚5.5 mm.管道左端固定，右端自由。文中的模拟环境较简单，不考虑噪声等复杂的外部环境，只考虑超声导波在管壁的传播。

图1 管道缺陷模型以及测点分布Fig.1 Damaged pipe model and probe position

其力学模型的单元选用Shell 63单元；在进行有限元划分网格时，管道轴向单元的单位长度为8 mm，环向均布24个单元；距离管道左端1.8 m处，通过改变单元的材料参数来模拟焊接(材料参数见表1)；将测点均匀设在距离焊缝8 mm的左右两侧，24个测点从x轴开始逆时针旋转排列。

表1 几何模型的基本参数Table 1 Material parameters of the bi-metal composite pipe

1.2 模拟结果

在缺陷程度为3.5 mm，60°(图2)的焊接管道最左端，沿着轴向施加如图3所示的位移激励。

通过对比可以发现，焊缝后测点的位移时程曲线图的第一个波包相对于焊缝前都有所衰减，而缺陷后对应测点的衰减更加明显，换言之，缺陷的存在对焊接管道中超声导波的传播产生了影响，这就是文中研究的突破口，若要进行损伤识别，首先要确定焊缝后测点所接收到的波包的由来。

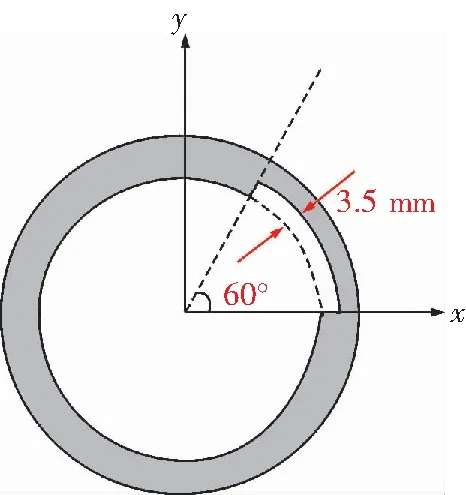
图2 缺陷程度示意Fig.2 Defect degree

图3 激励信号Fig.3 Pumping signal

图4 焊缝缺陷前后测点的位移时程曲线对比Fig.4 Guided wave signal by the probes before and after defects(后测点的第一个波包是由前测点的第一个波包通过焊缝透射得到，详见2.1)

2 损伤识别

2.1 损伤指标

对无缺陷的焊接管道进行模拟，同样加载，取管道最右侧端点为测点，得到其位移时程曲线图，如图5所示。从图5可见，在t时刻，测点开始接收到波，由此可以计算得到导波在管道中传播的速度5 169 m/s.此波速值可用于接下来的计算。

首先，对焊缝前测点的波包进行核实，以S1测点为例(图6)，在t时刻，测点接收到导波信号，可以计算出测点距离初始激励位置(管道最左端)的距离为1.794 m，这与焊缝前测点距离左端的实际距离1.792 m基本一致。

图6 S1测点位移时程曲线Fig.6 Guided wave signal by the probe S1

综上分析，焊缝后测点的第一个波包是由焊缝前测点的第一个波包通过焊缝透射得到，两者相对应，这为接下来的分析奠定了基础。

文中1.2已提出，缺陷的存在会对超声导波的传播产生较大影响，但是无法通过观察位移时程曲线图准确定位缺陷，更不能准确判断缺陷的程度。因此需要定义一个损伤指标使这种前后波形的变化更加具体。其定义如下。

图7 测点的位移时程曲线Fig.7 Guided wave signal by the probe

将缺陷前测点的位移时程曲线图中第一个波包的峰值记为a；缺陷后测点位移时程曲线图对应波包的峰值记为b，将a/b定义为损伤指标。即

Dindex=a/b

(1)

2.2 算例分析

研究对象虽是含有缺陷的焊接管道，但仍有必要先对无缺陷的焊接管道进行初步研究，观察焊缝对超声导波传播的具体影响。通过数据处理得到损伤指标分布，如图8所示。

图8 无缺陷焊接管道损伤指标分布Fig.8 Distribution of damage index of defect-free welded pipe

对于理想的焊缝，在管道一周，损伤指标均为2.2.以下考虑含缺陷焊缝，通过改变单元实常数来模拟不同的缺陷角度和厚度，得到以下12种不同工况。工况1～6，重点考察缺陷径向参数对损伤指标的影响，工况7～11重点考察缺陷环向参数对损伤指标的影响。

首先，分别对相同角度(30°)不同厚度缺陷的6种工况进行模拟，将无缺陷的焊接管道作为基准，得到一系列的损伤指标环向分布图(图9)。

图9 同种角度不同厚度工况的透射率倒数Fig.9 Reciprocal of transmission about different thickness of the same angle

工况缺陷环向角度/(°)缺陷径向厚度/mm1300.52301.53302.54303.55304.56304.87603.58903.591203.5101503.5111803.5

从图9可以看出，随着实际模拟缺陷厚度的增加，尖点到基准图的最短距离也在变大。因此，可通过分析二者之间的关系来得出检测缺陷厚度的方法。

如图10所示，将实际厚度定义为x，缺陷图中最高尖点到基准图的最短距离定义为测量厚度y，通过曲线拟合，可以得到y与x的关系。

图10 测量厚度与实际厚度之间的关系Fig.10 Relation between measured thickness and actual thickness

测量厚度y和实际厚度x之间的关系可以拟合为直线d2=0.95*x-0.45(图10)，因此，根据两者的拟合关系，由数据处理得到的缺陷的测量厚度，即可得到缺陷的实际厚度，从而达到检测缺陷厚度的目的。

接下来对同厚度(3.5 mm)不同角度缺陷的6种工况进行模拟，将无缺陷的焊接管道作为基准，损伤指标分布情况，如图11所示。

图11 同厚度不同角度工况的透射率倒数Fig.11 Reciprocal of transmission about different tangle of the same thickness

从图11可以看出，随着实际缺陷角度的增大，缺陷图相对于基准图的张角也在增大，而且无论角度如何变化，图像总是关于实际缺陷角度的角平分线对称。如图中标注所示，将实际角度定义为x，缺陷图与无缺陷图的交点(张角处)分别与原点连线，将其夹角定义为测量角度y，将二者进行拟合(图12)。

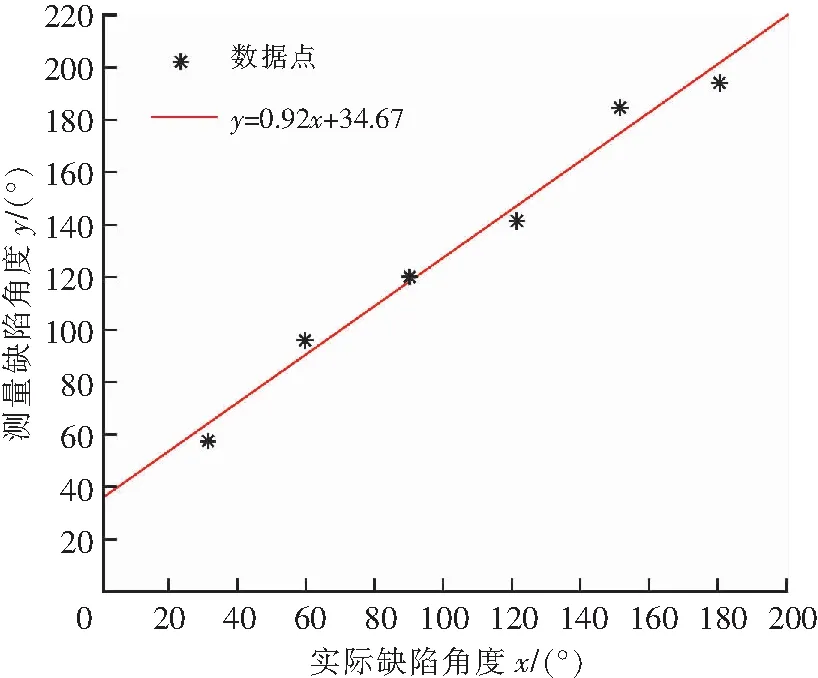
图12 测量角度与实际角度之间的关系Fig.12 Relation between measured angle and actual angle

这样不仅可以定位缺陷，还可以根据拟合的直线方程y=0.92*x+34.67，由测量的缺陷角度来确定实际的缺陷角度，从而达到检测缺陷角度的目的。

3 结 论

1)随着实际缺陷的角度和厚度的变化，损伤指标也发生了明显变化，说明该方法可以对焊接管道的缺陷进行识别；

2)缺陷的测量厚度和实际厚度、测量角度和实际角度之间都存在较好的线性关系，根据这种关系，不仅可以定位损伤，而且可以更准确地检测缺陷的径向和环向尺寸，对实际工程中的检测工作有很好的参考作用。