运用下垂控制的并网储能系统惯量阻尼特性分析

修连成,熊连松,康志亮,宋汉梁

(1.四川农业大学机电学院,611130,成都;2.南京工程学院自动化学院,211167,南京;3.香港理工大学电机工程系,999077,香港)

近年来,随着电力电子技术的飞速发展,电网中的电力电子装备占比急剧提高,越来越多的电能需要经过变流器处理。与此同时,传统的旋转式同步发电机(RSG)的装机比例逐渐降低,以低惯量、弱阻尼为特征的分布式能源在电网中的比例不断增加,给电网的稳定运行带来了安全隐患[1-4]。所以,现在的并网变流器系统控制将不能只考虑并网变流器系统自身的稳定性(自稳性),也需要并网逆变器与电网友好互动,在辅助提升电网稳定性的前提下获得自身稳定运行的环境,即必须具备辅助电网稳定运行的能力(致稳性)[5]。为此,学者们提出利用储能系统来平抑系统功率波动,增强电网的频率稳定性,同时等效地提高电力系统的惯量水平与阻尼能力。

图1 下垂控制的并网储能系统

为了充分发挥储能系统稳定电网的性能,现有的致稳性控制策略主要分为频率下垂控制、虚拟惯量控制和虚拟同步发电机(VSG)控制。仿照RSG一次调频原理,并网变流器需要频率下垂控制,使并网变流器系统主动响应电网的调频需求。频率下垂控制具有较高的可靠性和灵活性,所以在并网变流器系统控制中获得广泛使用[6-11]。虚拟惯量控制通常在一次能源供电侧进行控制,而并网变流器采用电压双闭环控制直流侧电容电压[12-14]。但是,在虚拟惯量控制的作用下,并网变流器的物理特性与现行电网的发电主体RSG有着明显的差别,并网变流器依然不具备RSG固有的大惯量、强阻尼特性,不能辅助提升电网的稳定性。VSG控制是基于一次能源调度算法和并网变流器的控制策略,使得并网变流器系统从外特性上模拟RSG的大惯量、强阻尼特性[15-18]。为了响应电网的调频需求,VSG控制一般不能独立运行,需要增加频率下垂控制环节[19]。

由于并网储能系统的动态稳定分析涉及系统很多变量,所以文献[20]提出了将系统动态过程的时间尺度特征划分为交流电流时间尺度、直流电压时间尺度、机械转速时间尺度3类来简化问题。其中,直流电压时间尺度动态过程对应于同步机发电系统中的机械时间尺度。文献[21]使用直流电压时间尺度的动态模型,发现下垂控制和VSG控制具有相似性,均可等效地模拟惯性效应,但该文献没有对频率下垂控制的并网逆变器系统惯性、阻尼以及同步特性的影响参数及规律进行分析,因此在改善电网惯量、阻尼特性方面仍不能充分利用频率下垂控制。此外,文献[22]提出了静止同步发电机(SSG)模型,分析了电压电流双闭环控制的并网变流器系统的惯性、阻尼以及同步特性。文献[23-24]构建并网变流器的直流电压时间尺度的动态模型,利用SSG模型分析了锁相环对并网变流器系统动态特性的影响规律。文献[25]使用SSG模型,提出了惯性效应可调的并网变流器系统控制方法。

本文构建了并网储能系统的直流电压时间尺度的动态模型,利用SSG模型,分析了下垂控制的储能系统惯性特性、阻尼效应以及同步能力,揭示了影响上述动态特性的内在机制、主要参数及影响规律。本文DC/DC变换器使用频率下垂控制策略从物理本质上对应了原动机的下垂控制特征,研究结果将有助于并网储能系统辅助提升电网的稳定性。

1 基于下垂控制模式的并网储能系统

本文以图1所示的两级式并网型储能系统为例,分析下垂模式下的储能系统惯量、阻尼特性。该并网储能系统包括储能装置、DC/DC变换器以及并网逆变器等。其中,DC/DC变换器工作于下垂控制模式,等效于常规发电机组中的原动机系统,并网逆变器工作于经典的电压电流双闭环控制模式,等效于常规发电机组中的RSG。Ub是储能装置的等效输出电压;Usk(k为a、b、c)是并网逆变器机端电压,对应SSG的励磁电势;Ugk是电网侧三相电压;L、R分别是滤波电感和线路电阻;ik是并网逆变器输出电流;udc是直流电容电压。

1.1 DC/DC变换器控制策略

在SSG模型中,储能装置可以视作常规发电机组中的一次能源(水力、燃煤、核能),DC/DC变换器对应于原动机(水轮机或者汽轮机),并网逆变器对应于旋转式同步发电机RSG,直流侧电容对应同步发电机RSG的转子部分。因此,根据SSG模型的视角,图1所示的并网储能系统可简化为图2所示的简化模型。

图2 并网储能系统的电路简化图

图2中,定义并网逆变器的输出电压为Us;δ是并网储能系统输出电压与电网电压之间的相角差。在忽略等效电阻的前提下,定义并网储能系统输出阻抗与线路阻抗之和为X。本文使用电网电压定向的同步旋转坐标系[26],如图3所示。

图3 dq坐标系下的矢量图

将电压、电流变换到同步旋转坐标系下,Park变换矩阵定义为

Tabc/dq=

(1)

则并网储能系统输出的电磁功率和无功功率分别表示为

(2)

(3)

根据图2、式(2)和式(3),可得并网逆变器输出的电磁功率、无功功率分别为

(4)

(5)

根据式(4)、式(5)可知,调节δ、Us、Ug和X都可以改变电磁功率Pe,而由于无功功率Q主要由电压Us决定,接入电网的电压Ug一般为定值,阻抗X为系统的结构参数,不方便改变,因此主要通过调节功角δ改变电磁功率Pe。并网逆变器输出的电磁功率Pe和输入功率Pin成正比关系,且在稳态时近似相等。显然,电网在额定角频率ω0下运行时,功率Pin输出为额定功率P0。由此可得经典的频率下垂特性曲线如图4所示。

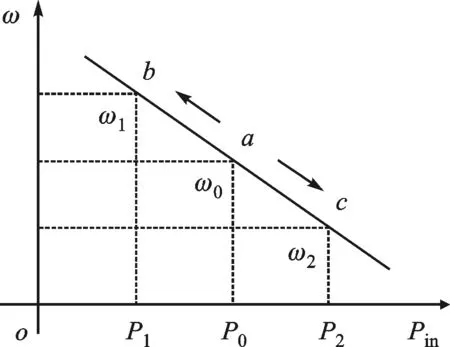
图4 经典频率下垂特性曲线

图4所示的频率下垂控制可描述为

ω=ω0-Dp(Pin-P0)

(6)

式中:Dp为频率下垂系数。因此,并网逆变器的输入功率为

(7)

若储能装置的能量足够充足,那么可参考电力系统的二次调频过程,利用DC/DC变换器的快速响应特性,实现电网频率的无差控制。根据式(7),在经典的频率控制环中加入积分控制器,即可实现并网储能系统的无静差控制,如图5所示。显然,图1中的DC/DC变换器使用图5所示的频率下垂控制之后,并网储能系统从物理本质上对应了常规调频机组的下垂控制特性和二次调频特性。

在图5所示的频率外环、电流内环控制策略中,电流内环的带宽一般远远大于频率下垂外环。对于频率下垂的外环控制过程而言,电流内环的动态过程在直流电压时间尺度下可以忽略不计,即

(8)

因此,考察直流电压时间尺度的动态过程时,根据式(8)和控制框图5所示的控制策路,得

(9)

式中:Di为频率控制环的积分系数。

1.2 并网逆变器控制策略

并网储能系统中的DC/AC电路采用电压电流双闭环控制来稳定直流电容电压,如图6所示。

恒压控制环的作用是输出指令电流使直流电容电压稳定,电流控制环的作用是按恒压控制环输出的指令电流进行快速跟踪。并网逆变器的恒压控制环采用PI控制,在控制策略中引入电压负反馈,实现无差控制。此外,可以根据不同控制目标分别给出无功电流指令。考虑到本文研究的储能系统主要提供有功功率支撑,因此可以令q轴电流指令为0。

同理,在直流电压控制时间尺度下,图6所示的控制过程可描述为

(10)

式中:Kp为恒压控制环比例控制增益;Ki为恒压控制环积分控制增益。

2 并网储能系统动态特性分析

文献[22]的研究表明:并网逆变器与常规RSG具有等效的动态模型、特征参数和能量传递过程,并据此得到了适用于并网逆变器系统动态特性分析的静止同步发电机模型,即SSG模型。

根据SSG模型可知,并网逆变器直流电压时间尺度的动态过程可用下式描述

(11)

式中

(12)

仿照电力系统中经典的电气转矩分析模型,式(11)可以改写成下述标准模型

(13)

式中:TJ为SSG的等效惯性系数;TD为SSG的等效阻尼系数;TS为SSG的等效同步系数。

上述3个参数分别表征了SSG的惯性水平、阻尼效应和同步能力。

本文将基于SSG模型的逆变器系统动态分析方法推广到了并网储能系统,并对基于下垂控制模式的并网逆变器系统进行了动态特性分析。

首先,根据图2、图3可知

(14)

在直流电压时间尺度下,根据式(10)、式(14),可得

(15)

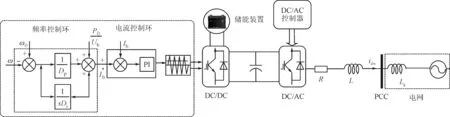
图5 改进型频率下垂控制框图

图6 并网逆变器恒压控制框图

对于小干扰稳定性分析而言,一般仅考虑变量之间的增量关系。因此,将式(15)线性化后,可得

sKΔδ=(sKp+Ki)Δudc

(16)

根据图1可知,DC/DC变换器输出功率的增量关系为

ΔPin=UbΔIb

(17)

将式(4)线性化之后,与式(16)、式(17)共同代入式(11),可得

(18)

将式(18)重新整理为式(13)所示的标准模型,即可得下垂控制模式的并网储能系统的SSG模型

(19)

根据式(19),可得到下垂控制模式的并网储能系统的Phillips-Heffron模型,其结构与RSG完全一致,如图7所示。

图7 改进型频率下垂控制的Phillips-Heffron模型

由此可知,基于下垂控制模式的并网储能系统在直流电压时间尺度上的运行机理与常规旋转式同步发电机RSG在机电时间尺度上的运行机理非常相似,均具有惯量效应、阻尼能力以及同步特性,且并网储能系统的惯性系数TJ、阻尼系数TD、同步系数TS分别为

(20)

由式(20)可知,下垂控制模式的并网储能系统,其惯量效应、阻尼能力以及同步特性由结构参数、控制参数以及稳态工作点同时决定。结构参数包括直流侧电容C、电网等效电感X、储能装置内电势Ub以及接入电网电压Ug等;控制参数包括DC/DC变换器频率控制环、DC/AC变换器电压控制环的控制参数;稳态工作点包括稳态功角δ0、稳态直流侧电容电压Udc、逆变器等效内电势US等。

从目前最受关注的惯量、阻尼特性在线控制的角度来看,调节储能系统的控制参数显然是最容易实施的惯量、阻尼特性控制方法。由式(20)可知:Dp和Kp即可等效调节系统的惯性效应,同时调节直流侧电容及其额定电压都可以等效调节系统的惯性系数。例如,当增大直流侧电容时,系统增大了对外来干扰的缓冲作用,提高了系统的惯性水平。调节频率控制环和电压控制环中的PI控制器都可等效调节阻尼系数。综上所述,通过频率控制环和电压控制环PI参数的优化设计,即可等效改变系统的惯性效应和阻尼特性。

此外,由式(20)还可得到下述结论:若Dp、Di、Kp和Ki同时为正数,则TJ、TD、TS也将同时为正数,即储能系统必然具有一定的惯性效应和阻尼水平,因此储能系统自身是小干扰稳定的,对应闭环控制论中的负反馈结构。显然,频率控制环节和电压控制环节的PI控制器是储能系统惯性效应与阻尼效应的主要来源,同时惯性与阻尼效应受到多个等效参数共同影响。需要特别说明的是,式(20)表明并网储能系统的惯量系数包括了和控制参数完全无关的组成成分,且该部分仅由系统自身的结构参数和稳态工作点决定。由此说明,并网储能系统天然地自带惯性效应,“储能系统自身不具备惯量效应”这一传统观点是不准确的。

3 仿真验证

本文基于MATLAB/Simulink仿真软件来证明下垂控制模式下的并网储能系统模拟惯性效应、阻尼水平和同步能力的有效性。仿真电路的拓扑如图1所示,主电路参数如表1所示,且电网在0.3 s时产生了10 Hz的频率变化扰动,使系统经历了一次扰动调整过程。

表1 并网储能系统的主要电路参数

3.1 阻尼特性验证

由式(20)可知,阻尼特性受到频率控制环和恒压控制环的PI控制器影响。在仿真实验中,调节Di时,并网储能系统阻尼特性的影响规律见图8。

图8 Di对并网储能系统动态参数的影响规律

仿真结果表明:随着Di的增加,直流侧电容电压udc的振荡幅度增大,振荡衰减变慢,即阻尼作用越来越弱,虽然结果中掺杂有同步系数变化的影响,但依然可以看到,Di越小并网储能系统对udc振荡的阻尼能力就越强,与式(20)得出的结论一致。由于调节Dp、Kp、Ki都可等效调节阻尼特性,同调节Di结果一致,所以不再赘述。

3.2 惯性特性验证

根据式(20)可知,系统的惯性系数受到Dp和Kp影响。Dp变化对并网储能系统抵御外界扰动的能力如图9所示。

图9 Dp对并网储能系统动态参数的影响规律

仿真结果表明:随着Dp的减小,udc振荡的幅度也减小了,并网储能系统对外部扰动的抵御能力(即惯性能力)增强,虽然有阻尼效应不同的干扰,但是仍然可以观察到,Dp越小并网储能系统抵御外部扰动的能力就越强,与式(20)得出的结论一致。较高的惯性水平有利于系统直流侧电容电压稳定,避免在外部随机扰动作用下出现直流侧电容电压波动过大,引起频率振荡。

在仿真实验中,调节Kp时,并网储能系统抵御外界扰动的能力影响规律如图10所示。

仿真结果表明:随着Kp的增大,振荡回归平衡时间变短,udc振荡的幅度减小,并网储能系统对外部扰动的抵御能力增强。仿真结果同时表明,Kp越大,udc的阻尼水平越大。由此可知,Dp不仅影响储能系统的惯性效应,也影响其阻尼水平。综上所述,当Kp值越大时,并网储能系统的惯性水平和阻尼能力就越强,与式(20)得出的结论一致。这表明Dp和Kp都可以等效调节惯性系数。

3.3 同步特性验证

由式(20)可知,调节Di和Ki,即可等效调节同步系数。Ki变化对并网储能系统同步水平的影响规律如图11所示。

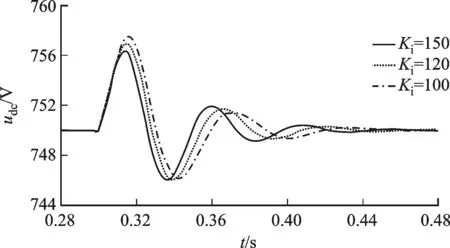
图11 Ki对并网储能系统动态参数的影响规律

仿真结果表明:随着Ki的增大,振荡回归平衡时间变短,并网储能系统对外部扰动的同步能力增强,虽然有阻尼能力不同的干扰,但是仍然可以观察到,Ki增大并网储能系统同步能力就越强,udc越能快速地恢复到稳态值,与式(20)得出的结论一致。图11显示,无论Ki怎么变化,udc的惯性效应几乎不变。由此可知,Ki几乎不影响系统的惯性效应,与式(20)得出的结论一致。调节Di和Ki,即可等效调节同步系数,结果与调节Ki一致。

综上所述,在不同的Dp、Di、Kp和Ki参数组合下,虽然udc的动态特性不一致,但最终均能稳定在设定值(750 V)附近,且偏差小于0.3%。主要原因是,下垂控制环节和恒压控制环节的PI控制器为并网储能系统提供了正的阻尼作用、正向的惯性效应和同步能力,因此并网储能系统能保持小干扰稳定。

3.4 仿真验证

(a)有下垂控制

(b)无下垂控制

本文使用MATLAB/Simulink软件对下垂控制模式的并网储能系统建模,导入基于RT-LAB的实时仿真平台进行验证。储能系统稳定运行一段时间后,向电网输出的功率为11 kW,随后电网产生一个50°的角变化。图12和图13为并网储能系统有下垂控制时和无下垂控制时的直流侧电容电压和有功功率对比。显然,有下垂控制时储能系统的udc可以在发生扰动后快速地到达平衡点(750 V),振荡衰减速度也明显快于无下垂控制时的储能系统。无下垂控制时,储能系统的有功功率在扰动后振荡衰减较慢,见图13b,有下垂控制时,储能系统可以较为快速地达到新的平衡点,见图13a。

(a)有下垂控制

(b)无下垂控制

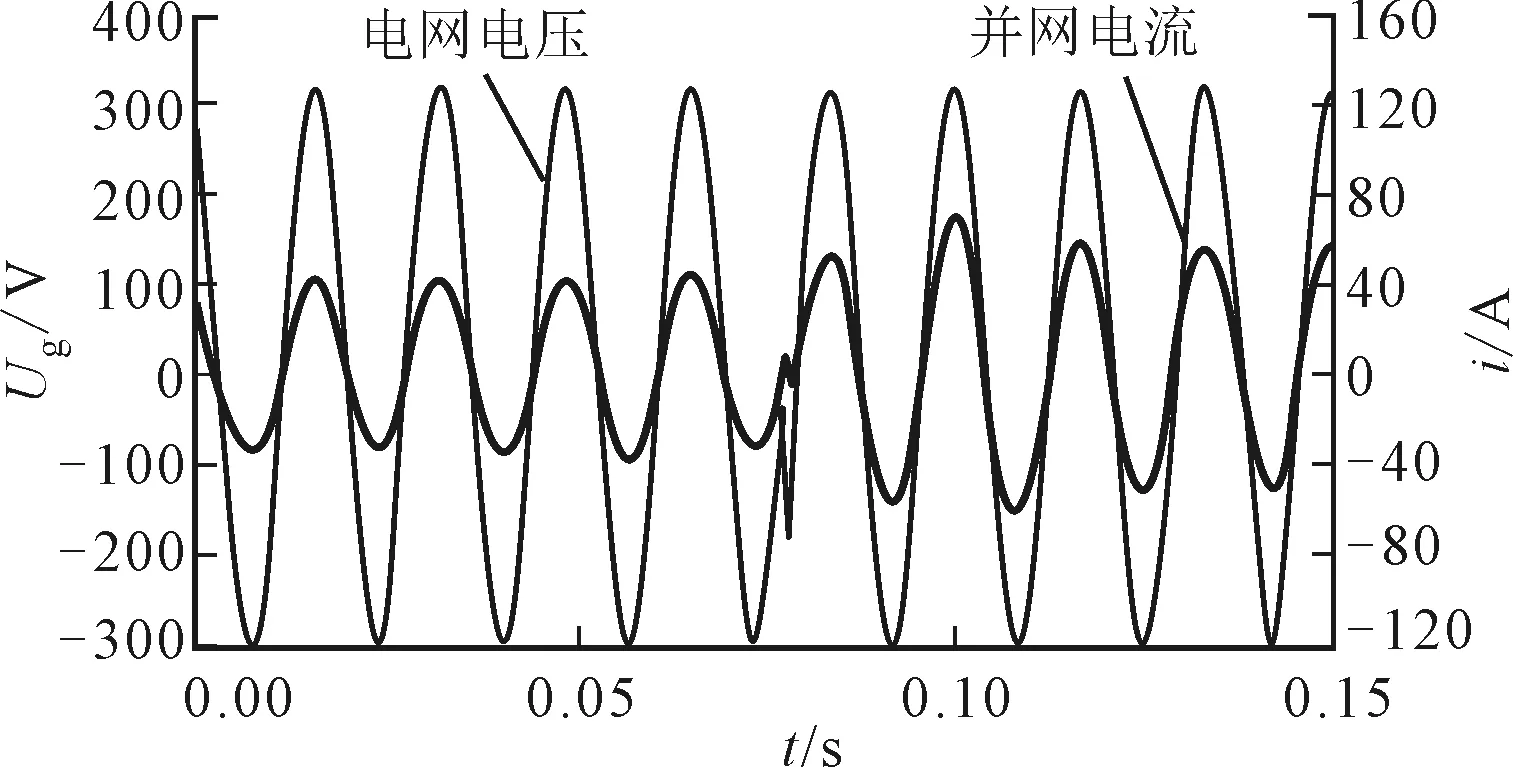
图14 电网电压和并网电流波形

图15 系统在功角变化扰动时的频率波形

图14表示下垂控制的并网储能系统电网电压和并网电流波形。图15给出了下垂控制的并网储能系统在功角变化扰动时的频率变化。不难发现,储能系统在一个较大的功角变化后,频率可在两个周期内达到平衡点。结果表明:在参数设计合理的前提下,直流母线电压udc在扰动过后可以快速地稳定在设定值(750 V);并网储能系统输出也可以快速地稳定在新的稳定点上。综上所述,下垂控制模式可以使并网储能系统快速地到达稳定点。

4 结 论

增强并网储能系统的惯性效应、阻尼水平及同步能力,有利于提高新能源并网发电系统的频率稳定性。本文通过构建并网型储能系统的直流电压时间尺度的动态模型,利用SSG模型分析了影响并网储能系统惯性效应和阻尼水平的内在机制、主要参数及其影响规律。研究结果表明:下垂控制模式的并网储能系统的惯量效应、阻尼能力以及同步特性由结构参数、控制参数以及稳态工作点同时决定,且并网储能系统惯性和阻尼效应的主要来源是频率控制环节和电压控制环节。显然,改变频率控制和电压控制中的相关参数就能等效地在线调节储能系统的惯性、阻尼以及同步效应。此外,本文储能系统中的DC/DC变换器与常规RSG发电系统中的原动机具有对应性,DC/DC变换器中的频率下垂控制使得并网储能系统具备了常规RSG发电系统的一次调频能力。