大规模网络图中4节点子图数量快速估计算法

覃遵颖,孙雨,李国栋,齐怀睿,陶敬

(1.西安交通大学智能网络与网络安全教育部重点实验室,710049,西安;2.西安交通大学 网络信息中心,710049,西安;3.西安交通大学电子与信息工程学院,710049,西安)

在大型复杂网络的子图集合中,存在着大量包含3～5个节点的小型无向子图,这类子图能够反映复杂网络的一些基础结构特性,对此类子图的数量进行挖掘分析,在生物学[1-2]、社会学、社交网络[3-6]和万维网分析[7-8]等领域都有着重要作用。例如,可以将具有特定功能的氨基酸团定义为蛋白质结构网络图中的一类小型无向子图[1-2],对这类子图进行数量统计,是认定蛋白结构、推定未知蛋白功能性质等工作的前提;类似地,将小规模用户之间的关系抽象为在线社交网络中的一类小型无向子图[9],对这类子图的数量进行统计,可以为分析在线社交网络中社团演化、用户聚类等工作提供思路。特别地,对于恶意代码网络图[10-12],研究人员可以将任意小规模的模块间的调用关系抽象为小型无向子图,对这些子图进行数量统计,可以推定未知软件中存在恶意代码的可能性,且响应速度和准确性都优于传统的文本检测方法。

Wang等的算法[13]对3节点子图数量的估计已经取得了比较好的性能,然而对于4节点子图数量的估计仍面临着较大的挑战,4节点子图定义结构如图1所示。现有的大部分4节点子图数量估计算法时间与空间复杂度过高,在实际使用中难以实现。为了解决这一问题,Jha等提出了3PS和C3PS算法[14],该算法使用节点采样估计的方法减小了计算量,然而却并未对估算结果的误差范围进行严谨地分析,未能从理论上严谨的证明C3PS算法一定能提高3PS算法的估算精度。

图1 4节点子图定义结构图

1 C3PS算法和3PS算法的误差分析

1.1 3PS算法及其误差分析

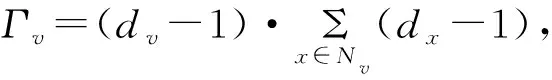
3PS算法的一次采样过程主要为5个步骤。

步骤1根据节点权重密度分布π={πv:v∈D},从节点集D中采样出节点v;

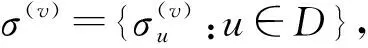
(1)

步骤3从节点v邻居集合剩下的元素Nv-{u}中随机采样出节点w;

步骤4从节点u邻居集合剩下的元素Nu-{v}中随机采样出节点r;

步骤5判断节点u、v、w、r能够构成的连通生成子图的种类。

在3PS算法的一次采样过程中,样本中节点u、v的度均要大于等于2,这说明一个4节点子图若要被3PS算法采样到,则其中至少要包含两个度大于等于2的点。根据图1中6种4节点子图的结构,第2种4节点子图中仅包含1个度为3与3个度为1的点,不符合采样条件,因此重复以上步骤K次得到网络图的K子图采样,可对第1,3,4,5,6种4节点子图的频数进行采样估计,估算结果为

(2)

式中:mi为样本集K中第i种4节点子图的数量;pi为一次采样中第i种4节点子图能被采样到的概率,pi=φi/Γ,其中φ1=1,φ2=0,φ3=4,φ4=2,φ5=6,φ6=1,φi为第i种4节点子图能被3PS算法采样到的次数;Λ3为网络图中度为3的点的数量。

3PS算法的估算误差满足如下定理。

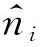
(3)

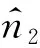
(4)

证明记P(X)为事件X成立的概率,Gsk为样本sk中4节点所能构成的连通生成子图的种类。当事件Y为真时,记A(Y)=1,当事件Y为假时,记A(Y)=0,则对于i∈{1,3,4,5,6},且k≤K,有

(5)

由于样本sk由随机采样而得,因此mi服从二项分布

x=0,…,K

(6)

mi的期望与方差分别为

(7)

(8)

Λ3-n4-2n5-6n6=n2

(9)

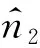
(10)

其中

C(A(Gsk=i),A(Gsl=j))=

E(A(Gsk=i)A(Gsl=j))-

E(A(Gsk=i))E(A(Gsl=j))=

0-pinipjnj=-pinipjnj

(11)

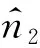
(12)

(13)

1.2 C3PS算法及其误差分析

C3PS算法的一次采样过程同样为5个步骤。

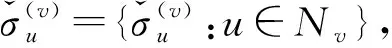
(14)

步骤3从Nv,u中随机采样出节点w;

步骤4从Nu,v中随机采样出节点r;

步骤5获取节点u,v,w,r构成连通的生成子图种类。

在C3PS算法的一次采样过程中若要采样到一个4节点子图,则其中至少要有两个点满足其Nu,v集合不为空。根据图1中4节点子图的结构,仅有第3,5,6种4节点子图符合采样条件。因此,C3PS算法通过重复以上步骤得到K子图采样,对第3,5,6种4节点子图数量估计如下

(15)

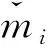
C3PS算法的估算误差满足如下定理。

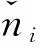
(16)

其证明与定理1类似,不再赘述。

1.3 复杂度分析

3PS算法的复杂度主要来自于采样算法的前4个步骤。步骤1中,为了计算出所有节点的采样权重,其复杂度为O(|L|),L为网络图中边的集合。步骤2中,为了能够根据节点的采样权重采样出节点v,其复杂度为O(lg|D|),D为网络图中节点的集合。步骤3中,从v的邻居集中采样出节点u,所需要的计算复杂度是O(lg|dv|)。最后,对节点w进行采样的计算复杂度为O(1)。因此,3PS算法的计算复杂度为O(|L|+Klg|D|),K为样本集的大小。

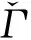
2 C3PS和3PS算法的准确度比较

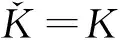
(17)

3 SmartMoss优化算法

本文设计了一种性能更好的4节点子图数量估计SmartMoss算法。

首先介绍本文算法对i=3,5,6这3种4节点子图数量的估计算法。由于3PS和C3PS两个采样器均可以对这3种4节点子图数量进行估计,定义如下

(18)

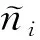
(19)

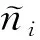
步骤1读入网络图G;

步骤2设定最大误差参数Smax,最大样本集参数Kmax;

步骤6若2|L|2/lg|L|≥Kp,则采用3PS算法对图G进行采样,跳转至步骤8;

步骤8若对图G的采样未完成,跳转至步骤4;

步骤9根据3PS算法和C3PS算法的估计结果,混合估计网络图中各4节点子图数量,并计算相应估计误差。

4 实验设计

4.1 数据集

本文在多个真实数据集上对理论分析结果以及本文算法的性能进行了测试,实验数据集来自Standard大学网络数据分析平台(SNAP)。表1详细给出了实验所用数据集的性质和特点。

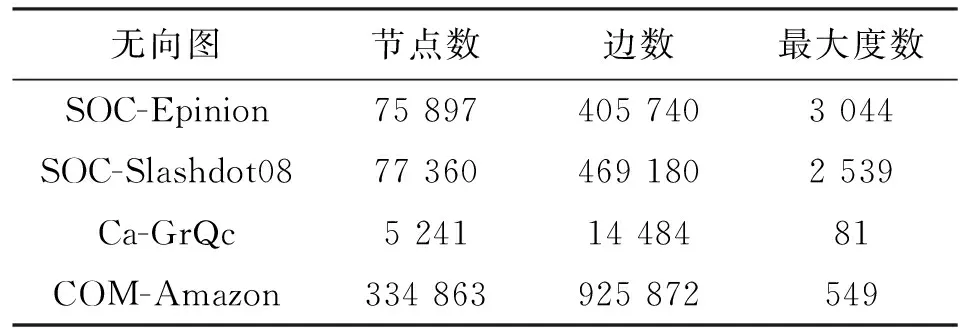
表1 实验数据集参数

4.2 性能指标

(20)

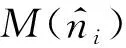
此外,本文根据定理1和2分析的理论结果,计算估计值的标准方差为

(21)

4.3 本文算法应用及准确度评估

为了验证本文算法的性能,在SOC-Epinions、SOC-Slashdot08和COM-Amazon这3个网络图上对本文算法进行了检验并对其准确度进行了评估。这3个网络图中分别包含有2.58×1010、2.17×1010和1.78×108个4节点子图,且第3,5,6种4节点子图的数量明显小于其他几种4节点子图。

(a)6种4节点子图数量真实值

(b)本文算法测量误差

图2a中分别给出了实验所用网络图中6种4节点子图数量的真实值,图2b给出了使用本文算法对6种4节点子图数量估算时的R和S。可以发现,出现频率较高的4节点子图拥有更小的S。在本实验中,参数设定为Smax=0.1,Kmax=105,且实验重复1 000次,计算平均结果和误差。实验结果表明,本文算法具有较高的准确性,而且误差分析的理论结果S可以准确地描述实际的估计误差。

4.4 本文算法与3PS和C3PS算法对比

本文算法可以根据中心极限定理及定理1和2给出的方差分析结论,估计达到预期的估计误差所需要的最小采样数。对比3PS算法和C3PS算法中最小采样数的估计,实验证明,本文算法更为准确。

本文在SOC-Epinions、SOC-Slashdot08和COM-Amazon这3个网络图上对两种算法进行了对比。当本文算法满足S≤0.01时,记预估所需的最小样本集大小为Ks,记满足相同条件时C3PS和3PS算法所需的最小样本集大小为Kp。对于SOC-Epinions、SOC-Slashdot08和COM-Amazon这3个网络图,Kp/Ks的值分别为38.6、20.9和17.0,这说明相对本文算法,C3PS和3PS算法的采样成本高出数十倍。本文算法性能优于3PS算法和C3PS算法。

5 结 论

本文研究了大型网络图中4节点子图的采样估计问题,提出了一种新的4节点子图采样估计SmartMoss算法,并通过实验对该算法性能进行了验证。通过理论分析与实验验证得出:首先,前沿算法C3PS能否提升3PS算法估算精度以及能提升多少取决于被测网络图的结构特征,C3PS算法并不一定能够提升3PS算法的估算精度;其次,本文算法通过被测网络的结构特性判断是否有必要使用C3PS算法提升子图数量估计的准确度,进而基于3PS和C3PS两种算法估算结果混合估计网络图中4节点子图的数量。对比实验同时证明,本文算法的准确率显著高于C3PS算法和3PS算法。