细菌模型的非协调混合有限元分析

毛凤梅,杨晓侠

(平顶山学院 数学与统计学院,河南 平顶山 467000)

0 引言

考虑细菌模型

(1)

其中:a11,a12,a22均为正数,X=(x,y,z),Ω为R3上的一个具有光滑边界的有界闭区域,I代表区间(0,T),T>0;u和v分别代表细菌的空间密度和被感染的人口密度;d1>0及d2>0为扩散系数;a11u表示细菌的自然死亡率;a11v代表传染病人口对细菌增加的贡献率;为传染病人口潜伏期所产生的阻尼项;g(u)代表在传染病流行中,当已感染人口总数不变的情况下的人口传染率且满足Lipchitz条件。

细菌模型描述了某些细菌在空气中的传播问题[1],怎样控制细菌传播速度和易感染人口的增长速度成为人们研究的热点。文献[2]用Leray-Schauder不动点定理证明了一类一维推广的细菌模型的周期解的存在唯一性;文献[3]用Green函数方法讨论了问题(1)周期平面波解的存在唯一性;文献[4]用Galerkin方法讨论了一类广义细菌模型的定解问题;文献[5]用Galerkin谱方法证明了二维广义细菌模型的整体解的存在唯一性;文献[6]给出了带有迁移的疟疾病和虐蚊数学模型的交替有限元方法和数值分析;文献[7]利用细致的能量估计、不同的希尔伯特空间的先验估计及一致的Gronwall不等式,证明了一类带有趋化性扩散的细菌模型一致有界解的整体存在性;文献[8]研究了一类噬菌体死亡率受到噪声干扰的随机噬菌体-细菌模型边界平衡点的随机渐近稳定性和随机模型的解围绕相应确定性模型正平衡点的震荡行为;文献[9]利用非协调元对细菌模型在全离散和半离散格式下进行了最优误差估计及超逼近分析。然而上述文献分析主要集中在传统的Galerkin方法,对此方程利用新混合元(特别是非协调和混合元)方法进行半离散和全离散误差分析的讨论目前少见报道。

众所周知,混合有限元方法是有限元领域中最活跃的分支之一,与传统有限元方法相比,具有可同时逼近标量函数(压力)和向量函数(流量)的优势,且引入通量后可改为在光滑度较弱的混合元空间中求解,但是该方法所涉及的两个逼近空间通常需要满足所谓的LBB条件。文献[10-11]提出了另外一种混合元格式,当选取的两个逼近空间满足一种简单的约束关系时,该格式自然满足LBB条件,避开了因梯度算子带来的麻烦,且在和传统格式同样精度的条件下,该格式需要更小的自由度规模,但他们在误差估计中仅得到了收敛性结果,没有涉及超收敛分析。后来,该方法应用到了二阶椭圆问题[12]、非线性四阶双曲方程[13]的超逼近和超收敛分析；文献[14-15]利用EQrot+Q10×Q01对广义神经传播方程和EFK方程在半离散和全离散格式下进行了高精度分析。

本文的主要目的是构造一个三维的非协调混合元(EQrot+Q100×Q010×Q001)用于研究具有实际背景的细菌模型,利用插值理论、高精度分析和对时间t的导数转移的技巧,借助于该单元所具有的性质,在半离散格式下分别导出了原始变量u,v的H1模和中间变量p,q的L2模下O(h2)阶超逼近结果和超收敛性质。进一步,通过构造适当的全离散格式,得到了精度为O(h2+Δt)的误差估计结果。

1 单元构造

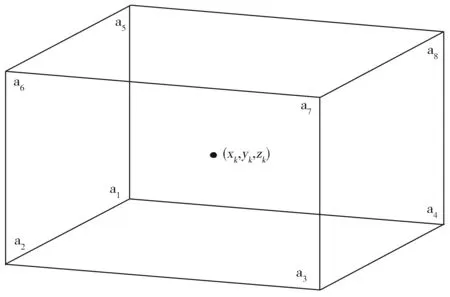
Fig.1 Cell partition diagram图1 单元剖分图

类似于文献[16]，定义混合有限元空间为

Wh={wh=(w1,w2,w3);wh|k∈Q100(K)×Q010(K)×Q001(K),∀K∈Th},

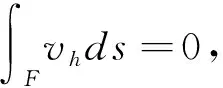
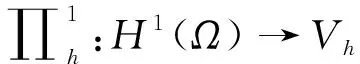
(2)

和

(3)

其中,n表示∂K上的单位外法向量。

类似于文献[16-18]可以证明如下结论

对于φ∈H1(Ω),ψ∈(H2(Ω))3,wh∈Wh,vh∈Vh,有

(4)

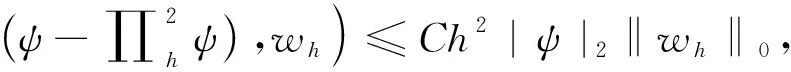
(5)

(6)

2 超逼近和超收敛分析

为了构造问题(1)的新混合有限元格式,引入变量p=-u,q=-v,则方程(1)可变为

(7)

(8)

相应的混合有限元逼近为:求{uh,vh;ph,qh}:[0,T]→Vh×Vh×Wh×Wh满足

(9)

定理1 方程(9)存在唯一解

在方程(9)中令χh=φi,zh=φi,Φh=Ψj,ψh=Ψj,则方程可变为如下形式

(10)

其中,

H1(t)=(h1(t),h2(t),…,hr1(t))T,H2(t)=(l1(t),l2(t),…,lr1(t))T,

G1(t)=(g1(t),g2(t),…,gr2(t))T,G2(t)=(s1(t),s2(t),…,sr2(t))T,

A=((φi,φj))r1×r1,B=((Ψi,

由(10)可得

(11)

由于(11)是关于向量H(t)=(H1,H2)T的非线性微分方程系统,由微分方程解的存在唯一性定理知,当t>0时,H(t)有唯一解[19],从而G(t)有唯一解,即问题(9) 存在唯一解。

下面给出上述问题的超逼近分析

定理2 设{u,v,p,q}和{uh,vh,ph,qh}分别是方程(8)和 (9)解,u,v,ut,vt∈H2(Ω),p,q∈(H2(Ω))3, 则

证明记

由(8)和(9)得误差方程:

(12)

在(12)(a)式中令χh=ζt,在(12)(a)式中令ψh=ζt再乘d1,两式相加得

(ζt,ζt)+d1(ζ,ζt)+a11(ζ,ζt)=

a12(τ,ζt)+a12(θ,ζt)-(ηt,ζt)-a11(η,ζt)-d1(η,

(13)

由于

(14)

根据结论(4)、(5)、(6), 插值理论,Schwartz不等式, Young不等式再结合(14)式, 方程(13)可估计为

C(‖τ‖0‖ζt‖0+‖θ‖0‖ζt‖0+‖η‖0‖ζt‖0+‖ηt‖0‖ζt‖0)+

从而,有

(15)

在(12)(c)式中令zh=θt,在(12)(d)式中令Φh=θt再乘d2,两式相加得

(θt,θt)+d2(θ,θt)+a22(θ,θt)=

(g(u)-g(uh),θt)-(τt,θt)+d2(δ,

(16)

类似于(13)式的估计, 再利用g(u)的Lipschitz条件,(16)式可估计为

从而,有

(17)

(15)和(17)式相加可得

对上式两边从0到t积分, 并注意到ζ(X,0)=0,θ(X,0)=0,得

再由Gronwall引理可得

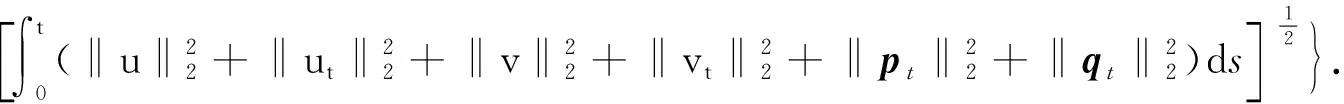
(18)

在(12)(b)式中令ψh=ξ可得

在(12)(d)式中令Φh=r可得

从而,定理2得证。

注:若新格式混合有限元空间选为Q111+Q011×Q101×Q110,当u,v∈H2(Ω),ut,vt∈H3(Ω) 时可得如下结论

显然此时对ut,vt的光滑度要求偏高,从而说明了本文所选单元的合理性和优势。

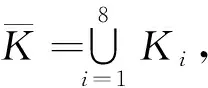
(19)

和

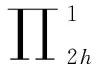
并成立如下结论

定理3 设{u,v,p,q}和{uh,vh,ph,qh}分别是方程(8)和(9)解,则

3 全离散及误差分析

首先将区间[0,T] 做n等分,0=t0

tn=nΔt, Δt=tn-tn-1,un=u(X,tn),

∂φn=(2Δt)-1(φn-φn-1),

由于以上记号,方程(8)可改写为如下形式

(20)

与(20)式对应的全离散格式为:求{Un,Vn;Pn,Qn}∈Vh×Vh×Wh×Wh,满足

(21)

定理4 设{un,vn,pn,qn}和{Un,Vn,Pn,Qn}分别是方程(20)和(21)的解,u,v,ut,vt∈H2(Ω),p,q∈(H2(Ω))3, 则

‖ζM‖h+‖θM‖h=O(h2+Δt), ‖ξn‖0+‖rn‖0=O(h2+Δt).

证明记

由(20)和(21)可得误差方程

(22)

在(22)(a)式中令χh=∂tζn,在(12)(a)式中令ψh=∂tζn再乘d1,两式相加得

(∂tζn,∂tζn)+d1(ζn,∂tζn)+a11(ζn,∂tζn)=-

(∂tηn,∂tζn)-a11(ηn,∂tζn)+a12(τn,∂tζn)+

(23)

下面我们对(23)式进行估计

d1(ζn,∂tζn)=d1(2Δt)-1(‖ζn+

(∂tηn,∂tζn)≤C‖∂tηn‖0‖∂tζn‖0≤

将上述结果代入(23)式可得

(24)

同理,在(22)(c)中令zh=∂tθn,在(12)(a)式中令Φh=∂tθn再利用g(u)Lipschitz条件,类似于(23)式的估计可得

(25)

(24)与(25)相加可得

(26)

对(26)式n从1到M求和

(27)

从而,有

(28)

选取适当的Δt和ε使1-CΔt-ε>0，再由离散的Gronwall引理, 有

‖ζM‖h+‖θM‖h=O(h2+Δt).

(29)

在(22)(b)中令ψh=ξn,可得

‖ξn‖0=O(h2+Δt).

(30)

在(22)(d)中令Φh=rn,可得

‖rn‖0=O(h2+Δt).

(31)