具有两个社团结构的复杂网络上的SIS模型

李金仙,付彩霞

(山西大学 数学科学学院,山西 太原 030006)

0 引言

传染病模型的建立及其上动力学行为的研究历来是学术界的热点问题[1-4]。近年来,关于复杂网络上的传染病模型的建立和分析有许多优秀的工作发表[5-10]。罗晓峰等[7]研究了在规则网络或随机网络上的SIS传染病模型,并证明了无病平衡点是局部渐近稳定的,地方病平衡点是全局稳定性的;张瑞霞[8]等人研究了无标度和小世界网络上具有染病时间延迟的SIS传染病模型,得到这两个网络的基本再生数,并通过模拟分析得到染病时间延迟将会减弱疾病的传播阈值的结论。Keeling[9]研究了局部空间结构对疾病入侵的影响,建立了随机网络或规则网络上的SIR模型,并得到模型的基本再生数和疾病的最终规模。社团结构是众多实际网络的一个共同的结构特征。如在食物链网中,社团可能是生态系统中的子系统;在万维网中,不同社团是不同主题的主页;在基因网中,社团是功能相关的蛋白质;在社交网中,社团是相互关系亲密的人群组。因此,在对复杂网络的结构性质的研究中,社团结构的研究应该是一个重要的研究领域[11-14]。彭小龙[13]等人研究了有两个社团的静态网络上的SIS传染病模型,并得到通过社团间的接触可以维持疾病的传播的结论。Tunc[14]等人研究了自适应网络上社团结构对疾病传播的影响,并指出疾病可以改变社团结构。

本文在文献[7]的工作基础上,研究具有社团结构的复杂网络上的SIS传染病模型。虽然彭小龙等人[13]也研究了具有两个社团的复杂网络上的SIS传染病模型,但是他们在研究网络结构对疾病的影响时,研究的是改变社团外部连边或社团内平均度对疾病传播的影响。事实上,当维持其它参数不变仅改变社团外部连边数或社团内平均度时,不仅社团结构发生了变化,而且网络的度分布也发生了变化。所以我们无法辨别对疾病传播的影响是由于度分布的改变引起的还是由于社团结构的改变引起的。为此,本文在保持网络的度分布不变的情况下,通过调节社团内外度的比例,从而改变社团结构,进而研究社团结构的改变对疾病基本再生数的影响。

1 SIS传染病模型

本节将给出具有社团结构的复杂网络上的SIS模型,并利用下一代矩阵得到该模型的基本再生数。首先介绍本文用到的一些记号。

1.1 基本记号

本文考虑具有N个节点的复杂网络G,G可以分为两个规模分别为N1和N2的社团,且N=N1+N2。我们分别记第l个社团的内平均度、社团外平均度和总连边数为nl,ml和Ml,这里l=1,2,并记L为社团间的总连边数。

我们用[]表示网络中节点数量、二元组的数量或者三元组的数量,用A、B、C来表示网络中节点的状态(易感者S状态或染病者I状态)。那么[A] 和[A]l分别表示整个网络或网络中第l个社团中状态为A的节点的数量;[AB]和 [AB]l分别表示整个网络或网络中第l社团中二元组A-B的数量也就是状态为A的节点与状态为B的节点实际存在的连边数;[AA]为状态为A的节点到状态为A的节点实际存在的连边数的2倍;[ABC]和[ABC]l分别表示整个网络或网络中第l个社团中三元组A-B-C的数量。由于社团内总边数保持不变,于是nlNl=[SS]l+[II]l+2[SI]l。染病节点发出的边数近似等于该染病节点I与易感节点S的连边数与该染病节点与染病邻居的连边数的和,从而,nl[I]l≈[IS]l+[II]l.

下面引入衡量社团强度的度量函数Q值[15]:

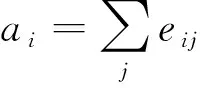
由于两社团外部连边数相等,故复杂网络参数之间满足如下相容性条件:M1-n1N1=M2-n2N2.

在相容性条件下,社团强度Q值可以表示为:

社团度量Q值越大,社团结构越强,社团度量Q值越小,社团结构越弱,Q值趋于0时说明社团结构已不存在,整个网络接近于随机网络,而当Q值接近于1时说明社团网络的社团结构很强[16]。在真实的接触网络中,Q值一般落在(0.3,0.7)[15]。

1.2 SIS模型的建立

首先,有N个节点的规则网络或随机网络中,当节点的平均度为n,聚类系数为零,并且节点的染病邻居服从多项分布时,SIS传染病模型[7]为:

(1)

其中λ为传染率,γ为恢复率。

本文将上述模型推广到有两个社团的复杂网络上,得到如下模型:

(2)

其中,i≠j,且i,j=1,2,λ12是社团间的传染率,

2 基本再生数

这一部分,应用下一代矩阵计算模型(2)的基本再生数[17]。令模型(2)的右端为0得到该模型的无病平衡点为Q0(0,0,0,0),由下一代矩阵方法,可以令:

则

依据下一代矩阵计算基本再生数的原理可知R0=ρ(FV-1),即FV-1的谱半径。

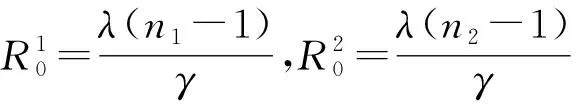
此时,我们有如下定理。

定理对于模型(2),当基本再生数R0<1时,无病平衡点是稳定的;当基本再生数R0>1时,无病平衡点不稳定。

3 数值模拟

本节将给出一些数值模拟来验证结论的正确性并探讨基本再生数随社团结构Q值的变化。

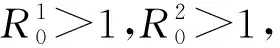
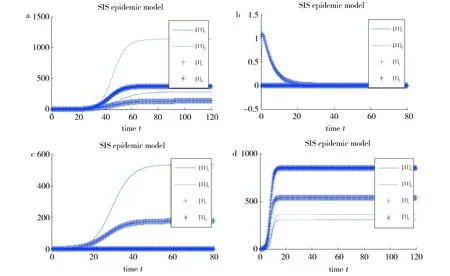
a:n1=12,n2=13,λ12L=100;b:n1=9,n2=6,λ12L=100;c:n1=13,n2=9,λ12L=100;d:n1=2,n2=2,λ12L=2 500Fig.1 Diagram of variation of number of infected [I]i and the pair [II]i with time when N1=1 000,N2=2 000,λ=0.1 and ν=1图1 当N1=1 000,N2=2 000,λ=0.1,γ=1时不同参数下两个社团内 染病者数量[I]i与二元组数量[II]i随时间的变化图

其中,

和

上式中的复杂网络结构参数M1,M2,N1和N2是给定的(即社团规模和平均度一定)的条件下,通过调节社团内、外度的比例来改变社团结构(即Q值),此时基本再生数相应改变。

图2给出基本再生数随着社团强度Q值的变化。图2结果显示随着社团结构的增强基本再生数可能是单调递增的,如图2a所示;也可能是先减少后增加而超过1,如图2b所示;也可能是先减少后增加但最终不超过1,如图2c所示。

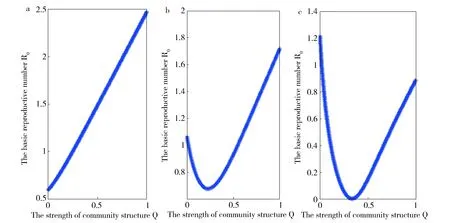
a:M1=4 000,M2=3 000,λ12=0.2;b:M1=4 000,M2=2 000,λ12=0.7;c:M1=1 000,M2=3 350,λ12=0.7Fig.2 Diagram of variation of the basic reproductive number R0 with community structure Q when N1=1 000,N2=2 000,λ=0.9 and ν=1图2 当N1=1 000,N2=2 000,λ=0.9且γ=1,不同参数下模型的基本再生数R0随社团强度Q的变化图

4 结论

文章主要关注含有两个社团的复杂网络上的SIS传染病模型,并利用下一代矩阵方法得到SIS模型的基本再生数,并通过数值模拟得到以下结论:一、本文得到了与文献[13]类似的结果,即对于SIS模型,疾病可能仅凭社团内部传播是传不开的,需要依靠社团间的传播来维系；二、单就社团结构对基本再生数的影响来看,社团结构的增强可能会增大,也可能减小疾病的基本再生数，这依赖于其他参数的取值或网络当下的社团结构。