基于灰色三角白化权SPA模型在水资源脆弱性评价中的应用

李庆昕

(辽宁省沈阳水文局，辽宁 沈阳 110094)

近年来，水资源系统的不稳定性随水资源的过度开采利用以及气候环境的变化而日益显现，对其脆弱性进行研究评价已成为水资源领域的主要研究方向和热点之一[1]。自20世纪90年代我国针对水资源脆弱性就开始了大量的研究和分析，并在脆弱性评价、含义以及内涵方面形成了一定的理论体系和研究成果，但整体仍属于水资源脆弱性研究的初始阶段[2]。流域水资源系统外部不仅受到压力驱动因素的作用影响，而且由于内部存在多个相互关联的子系统系统同时受到许多不确定性因素的作用[3]。所以，应同时考虑外部与内部因素对评价等级标准的综合作用影响从而更加精确、客观的确定各顶级的阀值，然而当前对水资源脆弱性研究中涉及到的相关内容相对较少，所建立的评价等级往往未考虑不同评价级别内各指标之间的同异反联系的影响作用[4- 6]。SPA集对分析理论可针对评价级别中不确定信息问题进行很好的分析和处理，据此本文在考虑了外部驱动与内部自然承载影响因素的条件下对联系度计算公式利用灰色三角白化权函数进行改进，并基于SPA基本理论构建改进的评价模型，以浑河流域为例对改进模型的有效性和合理性进行验证，以期为该流域水资源的规划建设和科学管理提供一定的理论支持和决策依据[7]。

1 构建水资源脆弱性评价指标体系

本研究结合浑河流域水资源脆弱性实际状况在充分考虑了系统外部压力驱动和内部自然承载能力的基础之上构建了三层次指标评价指标体系，见表1。其中B1～B2分别代表内部自然承载因素和外部压力驱动因素；C1～C7分别代表评价指标人均水资源占有量、降水量、流域产水模数、径流系数、干旱系数、生态环境需水比例以及水质等级；C8～C14分别代表评价指标人均GDP值、万元工业增值用水量、灌溉率、农业用水比例、水资源利用率和耗水率。

本研究依据水资源脆弱性等级标准相关数据资料和参考文献将脆弱性等级划分为非常脆弱、比较脆弱、中等脆弱、较不脆弱以及不脆弱5个标准。结合研究流域实际状况经多次合理分析和修正不同评价等级的阀值范围见表2。

2 建立灰色三角白化权SPA模型

2.1 集对分析理论

由中国学者在1989年提出的对于不确定性问题处理的方法即集对分析理论，其基本原理和过程是先在不确定性系统中构建两个相互关联集合的集对，并将集对进行异同性和差异性分析，然后采用合理的计算方法将集对进行“亦同亦反”联系度计算，构建集对以及对联系度计算是是集对分析法的基础和关键工作[8- 11]。SPA模型的核心理论是利用计算公式对分级标准和样本两个相互关联的集合进行各指标的联系度计算分析，并定性的对各评价指标进行评估，然后对整个系统结构体系框架进行综合性的评价。可利用下述公式进行联系数的求解：

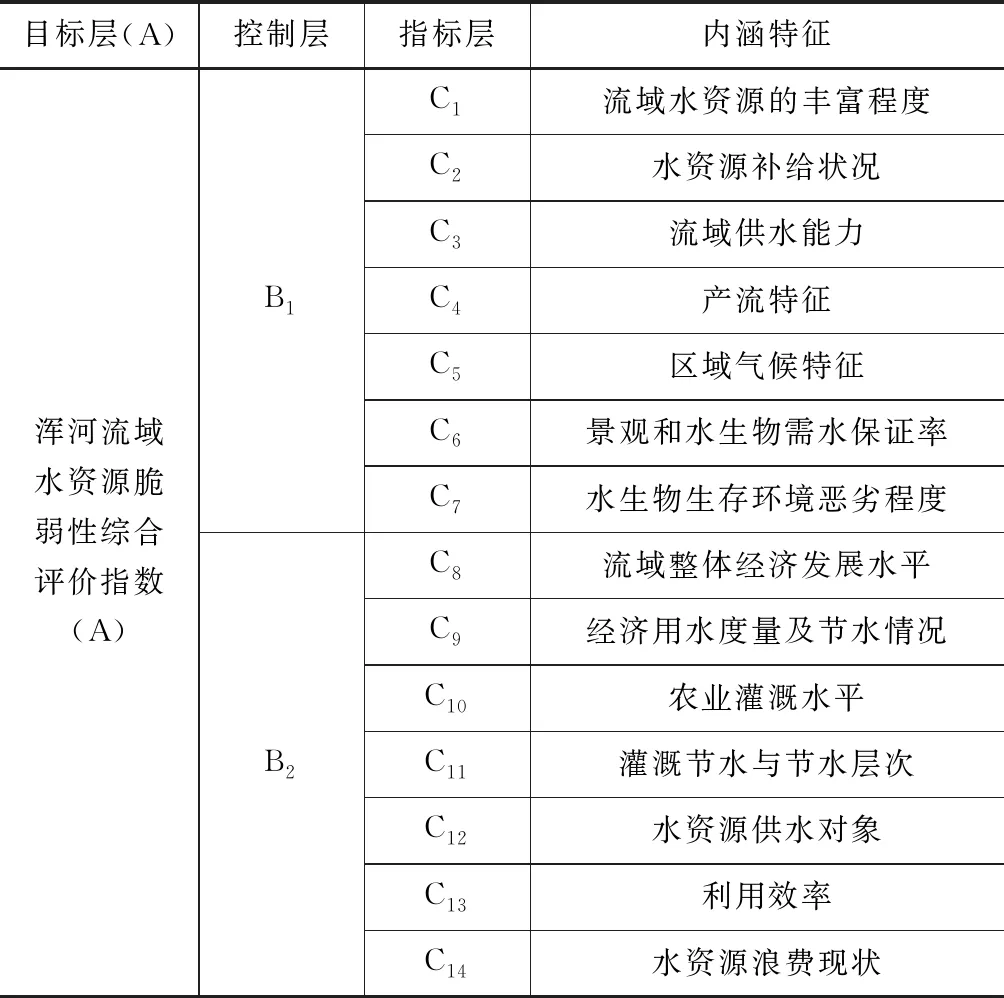
表1 浑河流域水资源脆弱性综合评价指标体系

μk=ak+b1ki1+b2ki2+b3ki3+ckj;k=1，2，，m

(1)

ak+b1k+b2k+b3k+ck=1;bik，ck∈[0，1]，i∈[-1，1]

式中，ak—指标同一度，代表样本对应于k评价指标的不脆弱等级水平；b1k、b2k、b3k—分别代表样本在不脆弱、中等脆弱以及较脆弱等级的水平；ck—对立度，代表样本在非常脆弱等级的水平。

按照均分原则对联系数隶属范围进行阀值空间的平均分割，从左至右可将其划分为四份并以i1、i2、i3、j分别代表四个节点值。同样可将空间平均划分为5个子空间，各子空间的取值范围为-1～-0.5、-0.5～-0.1、-0.1～0.3、0.3～0.5、0.5～1.0，各子空间范围所对应的水资源脆弱性评价等级依次为非常脆弱、较脆弱、中等脆弱、较不脆弱以及不脆弱。系统结构中的m个指标的评价等级过程如下。

(1)利用式(1)对样本值x可求得各个等级的分量和五元联系数μk值，从而可评估各个分量并求得各指标值对应于样本的隶属等级。

(2)对各个样本的五元联系数μ值进行求解并得到不同指标的权重ωk，然后可对脆弱性进行定性的表述，计算公式如下：

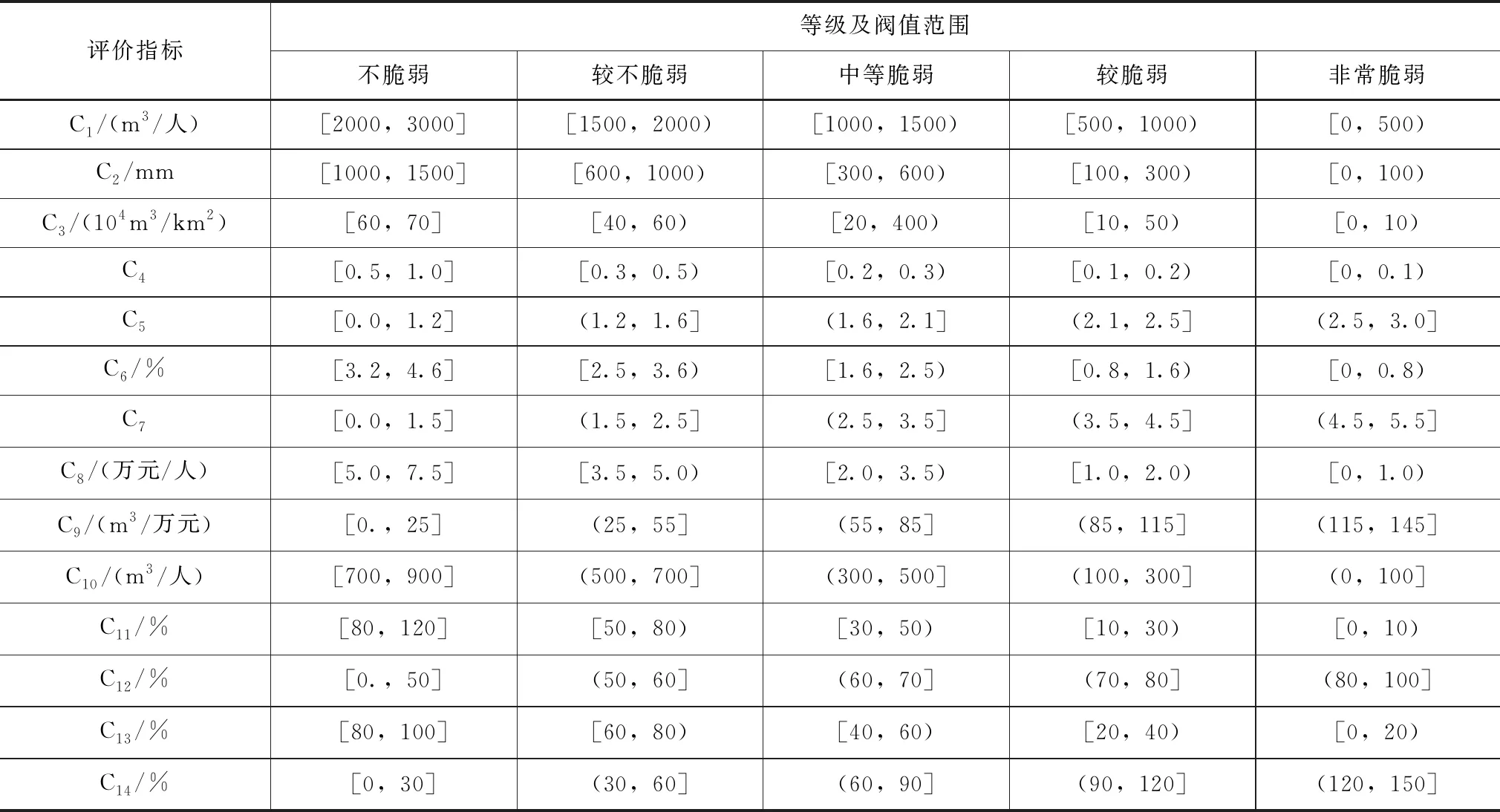
表2 浑河流域水资源脆弱性评价等级及分类标准

(2)

对各评价指标权重的计算求解应综合考虑各种主、客观因素的作用影响，从而更加准确、全面的对研究区域的水资源脆弱性进行评价分析。

2.2 改进的SPA模型

对评价等级标准中的不确定性问题利用传统的SPA模型不能较好的进行处理解决，从而对水资源脆弱性评价结果可造成显著的偏差。据此，对未知信息进行淡化处理的有效方法为灰色白化权函数聚类分析法，它可对系统本质的不确定性、模糊性信息进行客观、准确的表征[12]。所以，本文利用三角联系函数并结合灰色聚类与SPA基本理论构建了评价指标的5个分级系统，对各分量利用聚类系数进行类比分析，其表达式如下所示：

(3)

式中，μjk—在j等级下对应于k评价指标的样本联系度分量。

将系统阀值利用不同评价等级可划分为[fj，fj+1]，引入λj=(fj+fj+1)/2，由此可对样本各指标在不同等级标准下的灰色聚类技术vjk进行求解，公式如下：

(4)

式中，xik—评价指标k在区域i中的样本值；

对各样本指标的灰色聚类系数vjk进行归一化统一处理，计算公式如下：

(5)

各指标的联系度分量可在求解μjk后进行计算，由此可对各指标的评价结果进行分析和研究。

2.3 指标综合权重的确定

客观赋权法通常会忽略不同评价指标的重要性程度的差异，以此可引起重要信息的丢失；而主观赋权法通常依据个人经验和理论认知对各评价指标进行赋权，该方法受个人因素和主观判断的作用影响其评价结果可能出现极端偏离真实结果的情况[13]。据此，综合集成赋权法是充分考虑了主、客观赋权法不足之处的基础之上，通过将二者有效的结合对水资源脆弱性评价指标的权重ω进行综合计算的方法。假定评价指标利用AHP法计算的权重为ω′，利用熵值法求得的权重为ω″，并利用距离函数d(ω′，ω″)表示两种方法计算的差异程度其表达式为：

(6)

可利用下式进行评价指标综合权重的求解：

ω=αω′+βω″

(7)

式中，α、β—分别为AHP法和熵值法的权重分配系数。

确保两种方法计算结果的一致性为组合赋权法理论的核心内容，所以上述公式需满足以下要求：

d(ω′，ω″)=(α-β)2

(8)

α+β=1

(9)

利用上述综合赋权法不仅可体现评价者的主观能动性，而且各指标数值为实测数据可反映区域的真实状况。

2.4 综合评价步骤

(1)首先采用式(4)并依据不同等级标准的取值范围和实测值xik可各指标的vij进行求解，然后利用式(5)对各指标的vij计算结果进行标准化归一处理，并求得样本在不用级别j条件下的μjk值。

(2)利用相关公式对各ak、b1k、b2k、b3k、ck值进行求解。

(3)各评价指标的无元联系数μk利用公式(1)进行求解，然后依据判定准则对各计算结果的合理性进行分析判别。

(4)在求得各指标ω′和ω″主、客观权重系数之后可利用式(7)～(9)进行各评价指标的综合权重系数ω的计算。

(5)对水资源脆弱性利用式(2)所求得的总体五元联系数μ进行评价和分析，并针对评价结果给出响应的建议和对策。

3 实例应用

3.1 研究区域概况

浑河发源于清原县，全长415km，流域总面积11481km2，年平均降水量约718.3mm，年蒸发量约为1805.4mm，年平均径流量为30.52亿m3。流域内属于不对称水系，东部坡陡谷深支流密集，而西部支流较少水量较低，其降雨规律为自东至西逐级递减，径流洪水受降雨量影响显著，降雨集中在7月和8月。气候为温暖带季风气候，温差变化较；浑河流域内农业人口数量增长过快并导致对耕地需求量明显增大，且土地被过度的开垦，农田灌溉用水急剧加大，水资源供需矛盾突出，水质污染和浪费现象严重，区域水资源脆弱性问题日益严重，不仅对人们的正常生活产生严重影响而且严重制约着区域农业经济的发展，开展脆弱性评估十分必要[14]。

3.2 评价分析

结合浑河流域现场勘测数据、统计年鉴以及水利部门提供的相关资料，对浑河流域2016年水资源系统的联系度分量利用灰色三角白化权集对分析模型进行计算和分析，计算结果见表3和如图1所示。由表3计算结果和图1可知，各评价指标之间的对立度ck计算结果值均为0，由此表明浑河流域水资源接近于非常脆弱评价等级的程度为0，水资源应用整体状况良好，评价指标C5、C6、C8、C9、C12、C14的μk值均在0.6以上，由此表明浑河流域在该6项指标表现为不脆弱性，水资源利用现状良好；然而在水质、水资源量以及人均占有量方面的评价结果值为-0.2以下，由此表明该项指标应用现状不容乐观，水资源的不合理开采利用以及节水技术相对滞后，水体应用环境、污染、供需矛盾突出等呈显著脆弱性。该流域相关部门应加大对水资源的开采利用管制力度，加强对河流水体污染的治理强度并改善当前水质现状，促进水生态系统的良性循环和发展。

表3 浑河流域水资源脆弱性综合评价结果统计表

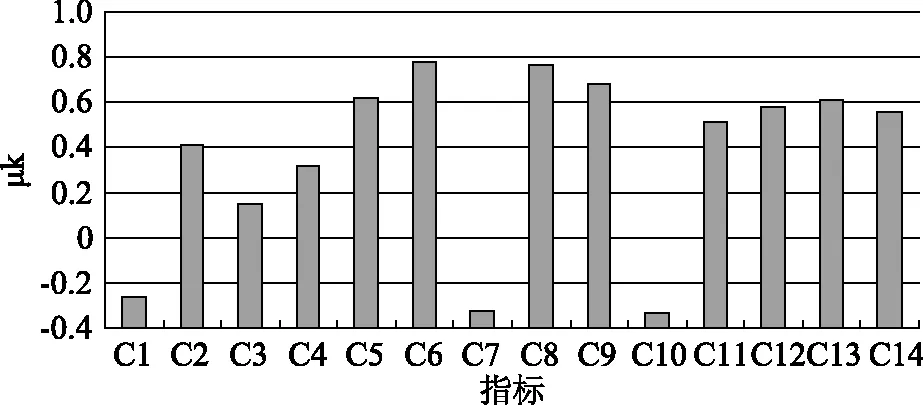
图1 各评价指标评价结果

利用式(4)～(6)并结合五元联系数评价和分析结果可求综合权重ω进行求解，其计算结果为ω=0.125 0.080 0.078 0.069 0.060 0.42 0.088 0.050 0.058 0.119，0.047)，其中系统结构内部自然承载评价字表和外部压力驱动评价指标的分权重计算结果分别为：

(0.225，0.152，0.146，0.126，0.108，0.078，0.166)

(0.107，0.130，0.261，0.1025，0.112，0.120，0.168)

总体评价结果μ值；利用式(2)进行求解为0.262，其中内部和外部作用因素的评价结果分别为0.148和0.402其分别处于中等和不脆弱评价等级，评估结果详细见图2。据图2可以知道，浑河流域水资源脆弱性在自然承载方面较为明显，而在内部评价方面较差，此研究成果研究流域实际状况保持良好的一致性。

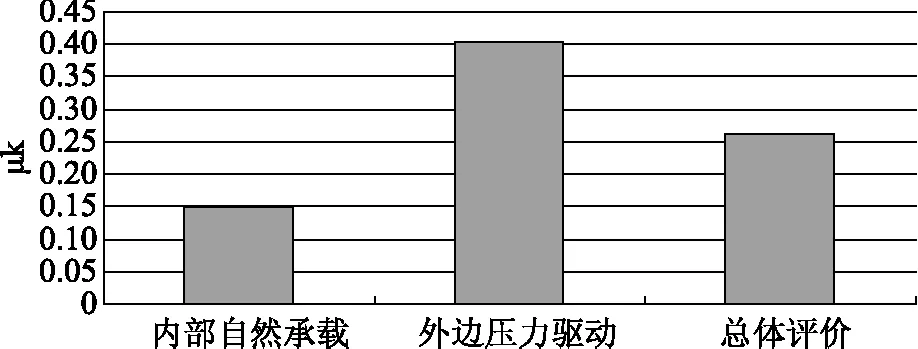
图2 μk综合评价结果

4 结论

(1)针对评价等级中的不确定性因素和模糊性信息利用灰色三角白化权函数的SPA模型可进行很好的处理和分析，其评价结果能较好的反映水资源的实际状况，利用该模型其评价结果更加合理可靠。

(2)利用主客观相结合的方法对ω进行求解能够更加贴近研究流域的实际状况，然而本研究在指标权重改进计算方面只是进行简单的叠加处理并未做更加深入的理论分析和研究探讨，故仍需要进一步深入研究。