三角形两解条件的一种巧记方法

■江西省丰城中学 吴爱龙 黄小华

在△A B C中,已知a,b和A,求解三角形。常用结论为：在A为锐角的情形下,若满足条件bsinA＜a＜b,则△A B C必有两解。

上述结论,常可借助图1来解释。此法不仅操作性不强,而且记忆困难。一旦将字母调换,就会造成一片混乱。

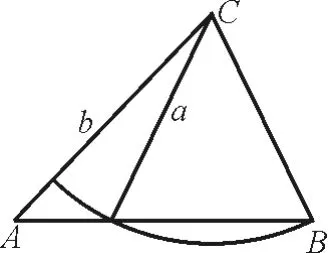
图1

下面借助单位圆中的正弦线,更直观地处理上述问题。

在△A B C中,由正弦定理知

如图2,记∠P OM=A(A为锐角),∠Q O H=B(B为钝角)。

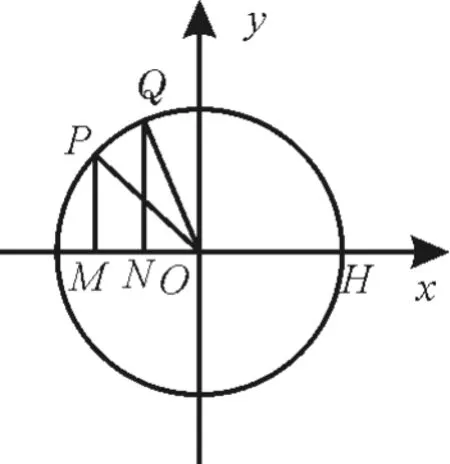
图2

由图显见,当|M P|＜|N Q|＜1,即 sinA＜时,亦即bsinA＜a＜b时,∠P O Q=C,此时,A+B+C=π,三角形存在一解。

同理,当B为锐角时,显然又有一解,所以△A B C共有两解。

利用上述方法判断三角形两解问题时,只需看题设是否满足条件|M P|＜|N Q|＜1即可,若满足则有两解。倘若将题设中的已知角称为“先角”,而由题设及正弦定理求出的角称为“后角”,则不等式“|M P|＜|N Q|＜1”可用文字语言表达成“先角的正弦值＜后角的正弦值＜直角的正弦值”,这些文字方便记忆。

例1在△A B C中,已知a=2,b=,A=45°,则满足条件的三角形有( )。

A.1个 B.2个

C.0个 D.无法确定

解析：由正弦定理,得sin。|MP|=sinA=,|NQ|=sinB=,满足条件|MP|＜|NQ|＜1,故满足条件的三角形有2个,选B。

例2在△A B C中,已知b=6,c=10,B=30°,则这样的三角形有( )。

A.0个 B.1个

C.2个 D.1个或2个

解析：由正弦定理知sin,|MP|=sin,|NQ|=sin,满足条件|MP|＜|NQ|＜1,有两解,三角形有2个,故选C。

例3在△A B C中,角A,B,C所对的边分别为a,b,c。若a=x,b=2,B=45°,且此三角形有两解,则x的取值范围为( )。

A.(2,22) B.22

C.(2,+∞) D.（2,22］

解析：由正弦定理知,则sin。|MP|=sinB=

由题设知三角形有两解,故必须满足条件|MP|＜|NQ|＜1,即,整理可得。故选A。

运用此法实际解题时不必画出单位圆,只需判断是否满足“先角的正弦值＜后角的正弦值＜直角的正弦值”即可,满足则有两解。