基于无滤波器高频方波注入的IPMSM无传感器控制策略
傅睿潇,黄守道,王海龙,王家堡
基于无滤波器高频方波注入的IPMSM无传感器控制策略
傅睿潇,黄守道,王海龙,王家堡
(湖南大学,长沙 410000)
本文提出了一种基于静止坐标系的高频方波电压注入方法。该方法是通过在()静止坐标轴系中注入高频方波电压,从而得到高频电流响应来估算永磁同步电机的转子位置。该方法采用高注入频率,从而可以减少转子电阻的影响,提高估计精度。其次,该方法在信号处理过程中无需滤波器的使用,因此控制系统的带宽得到了提升。此外,为准确地估计转子位置,本文采用了比传统PI观测器的估计精度更高、抗扰动能力更强的扩张状态观测器(Extended State Observer,ESO)。最后,在一台1.5kW的内置式永磁同步电机上进行了实验,实验结果证明了在低速情况下本文提出的无传感器控制方法能取得优异的结果。
内置式永磁同步电机;无位置传感器;高频注入;低速;ESO
0 前言
永磁同步电机因其转矩密度大、效率高而在电动车驱动、舰船推进、数控系统及家用电器等领域得到广泛应用。高性能的永磁同步电机控制技术如矢量控制需要转子精确的位置信息。通常转子位置信息由机械式位置传感器获得,然而该传感器的安装会增加系统的成本和尺寸,并降低系统的可靠性,且在特殊环境中无法使用机械式传感器,为了解决以上问题,国内外学者提出了无位置传感器控制技术[1-3]。
永磁同步电机无传感器策略主要有滑模观测器、扩展卡尔曼滤波器、模型参考自适应控制[4-6]。这些方法都是通过检测反电动势再利用电机模型得出转子位置,然而在低速甚至零速的情况下,反电动势幅值太小,信噪比太低,因而无法准确提取来估计转子位置。相比之下,高频注入法在低速和零速下有着较大的优势[7-9]。高频注入法基于电机凸极性,利用包含转子位置信息的电机高频模型电感矩阵来实现无传感器控制,通过注入高频电压或电流信号,可以从响应信号中提取转子位置。
本文提出了一种基于静止()参考系的方波电压注入无传感器控制策略,通过将高频方波电压注入到定子静止参考系的()轴上,高频响应电流将随位置改变而波动,从而得到转子位置。整个信号处理过程中无需使用滤波器,可以大大提高系统带宽,注入高频方波信号可以更好地消除定子电阻的影响。同时,采用ESO进行转子位置观测,提高了收敛速度和控制精度和抗扰动能力。最后,进行了仿真和实验的验证,证明了该方法的有效性。
1 IPMSM数学模型
IPMSM在旋转坐标系下的电压数学模型为
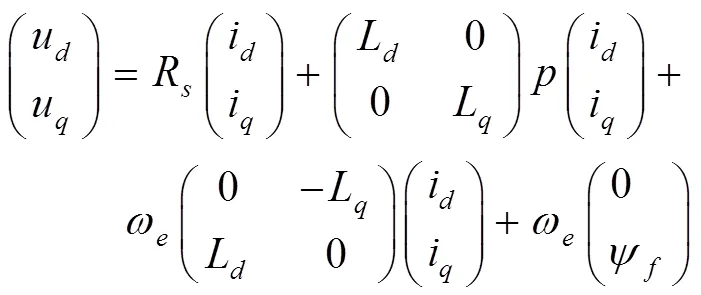
式中,u,u分别为轴电压分量,i,i分别为轴的电流分量;R代表定子电阻;L,L分别为定子轴电感;表示微分算子;ω为转子电角速度;Ψ表示永磁体磁链。
从旋转坐标系到静止坐标系有转换矩阵
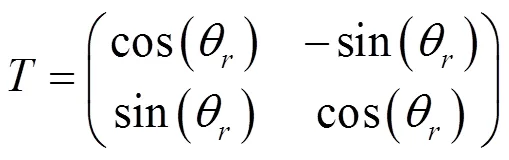
于是把式(1)通过转换矩阵变换到两相静止坐标系得到:
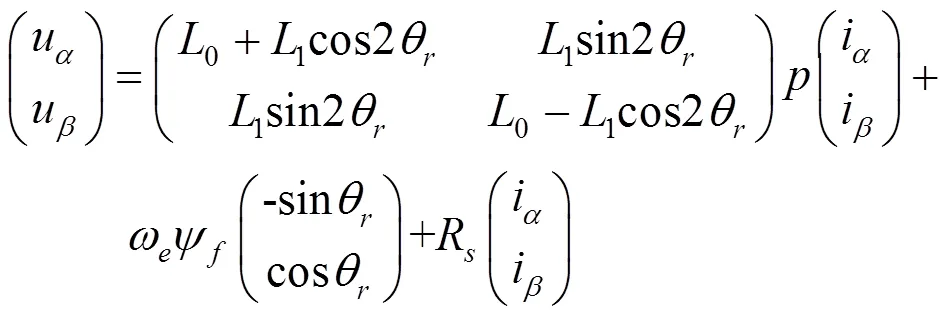
式中,u,u分别为静止两相坐标系轴电压分量;i,i分别为静止两相坐标系轴电流分量;0表示均值电感有0=(L+L)/2;θ表示转子电角度;1表示差值电感有1=(LL)/2。
向定子绕组注入高频电压信号时,若信号的频率远高于基频,可以把此时的永磁同步电机看作是个纯感性负载,且此时反电动势的值很小,可以忽略,因此静止两相坐标系下的高频激励电压方程为:
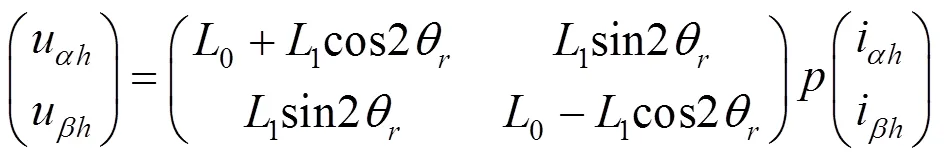
式中,u,u分别表示两相静止坐标系轴高频电压分量;i,i分别表示两相静止坐标系轴高频电流分量。
对(4)进行变换可以得到:

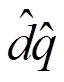
2 高频注入无位置传感器控制策略
2.1 方波注入无位置传感器控制策略
本文提出了一种方波电压注入方法。通过注入高频方波电压在()静止坐标系上来得出转子位置[10],适合于低速和零速的情况,并且整个过程不需要任何滤波器的使用,使得系统带宽和注入频率都扩展到了更高。
选取轴进行方波电压注入,注入电压表达式如下式(6):
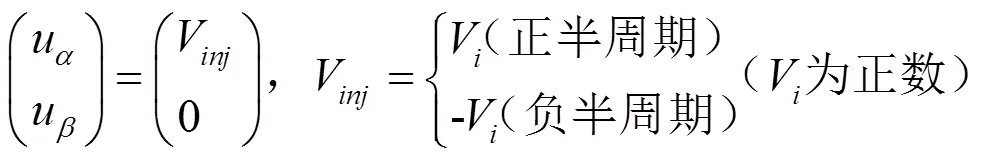
注入的方波电压频率可以达到很高。此时注入信号的频率远远高于基波频率,永磁同步电机可以看作一个纯感性负载,定子绕组的影响几乎可以忽略。根据方波注入原理,把式(6)带入式(5)中可以得到:
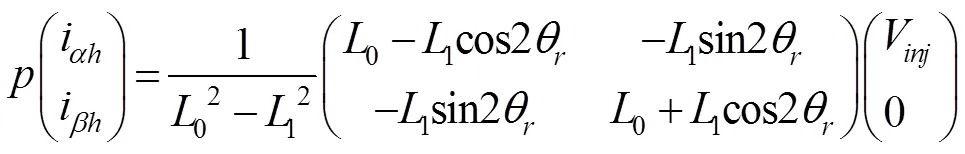
将式(7)进一步变换得到:
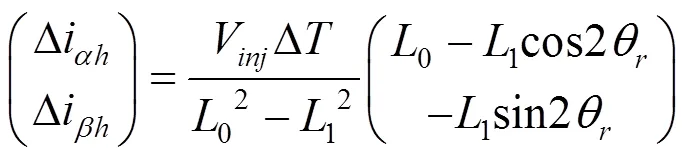
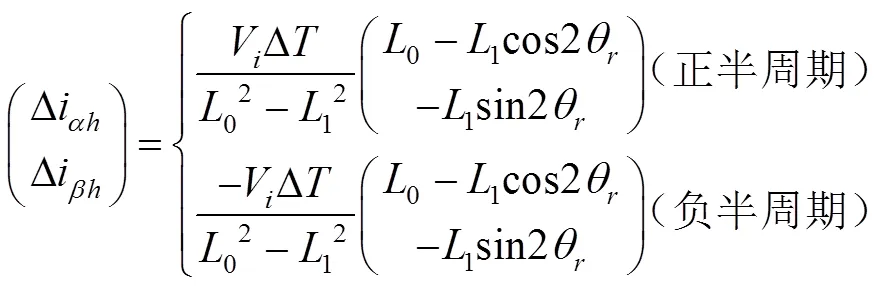
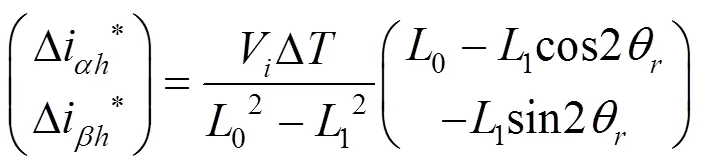
由(10)化简得:
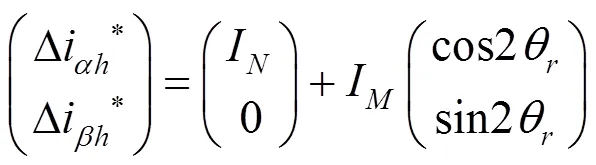

I表达式中的元素都是已知量,I可以计算得到,在注入信号幅值频率不变的情况下,可以认定I为恒值。通过直接计算得到直流偏置I。式(11)减去I再标幺化去除I后得:
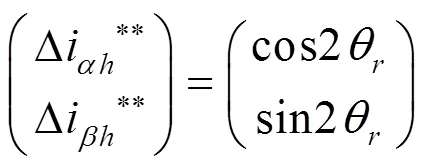
把式(13)通入转子位置观测器可以得到估计的转子位置θ。
2.2 无滤波器高频信号分离
通常情况下,所有的高频注入法都是在注入高频信号后,把高频电流响应从定子电流中分离出来,再进行信号解调得出转子角度。这通常都会使用到数字滤波器。然而数字滤波器的使用限制了系统的带宽,降低了位置观测响应速度,会造成相位延迟,且高阶滤波器的使用会使得处理复杂,计算量大增[11]。于是本文提出采用一种无滤波器的高频信号分离方法。
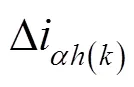
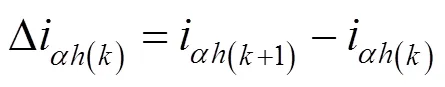

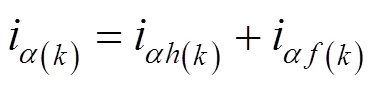
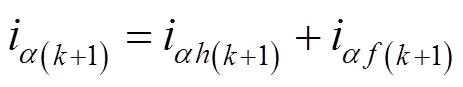
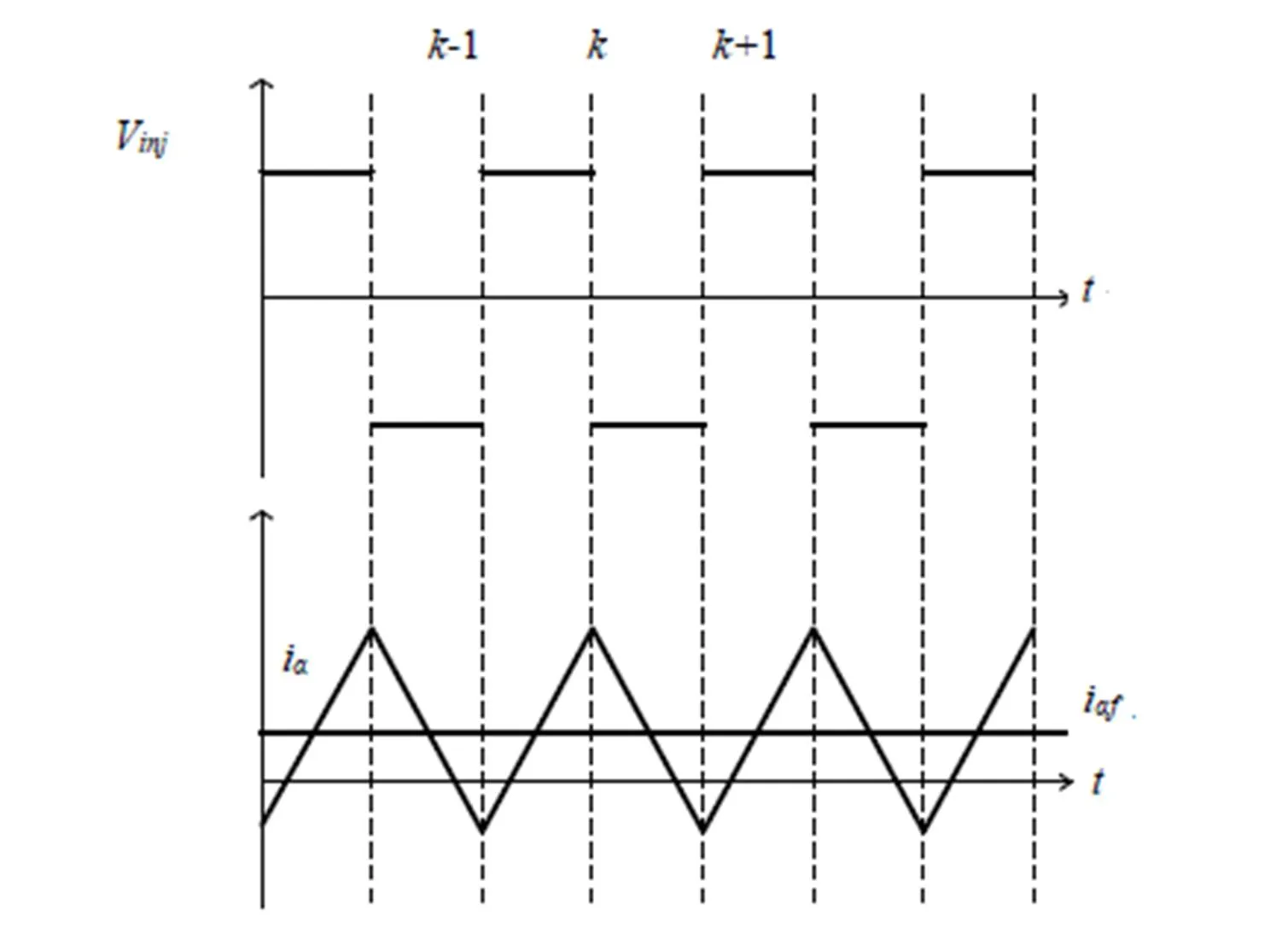
图2 高频电压信号和响应电流信号的时序图
由于相邻采样时刻定子的基波电流信号幅值可以假定不变,则通过数学计算就可以实现高频信号分离,利用(17)减去(16)可以得到:

通过该无滤波器高频信号分离方法,代替了传统方法中的高通滤波器或带通滤波器,有效地提高了系统带宽,减小了计算量,加快了位置观测响应。
2.3 转子位置估计
为了从式(13)中得到转子位置,把两路信号通过一个正交锁相得到转子实际角度和估计角度差值的正弦值,如式(19)所示:

通常控制周期远远小于机械时间常数,所以在一个控制周期内,我们可以认为转矩是固定不变的,写出简化的三阶状态方程[12]。

那么ESO的闭环传递函数为


图3 ESO控制框图
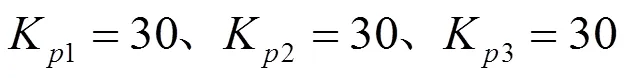
此时系统带宽3dB=47Hz左右。图4所示为观测器的伯德图。
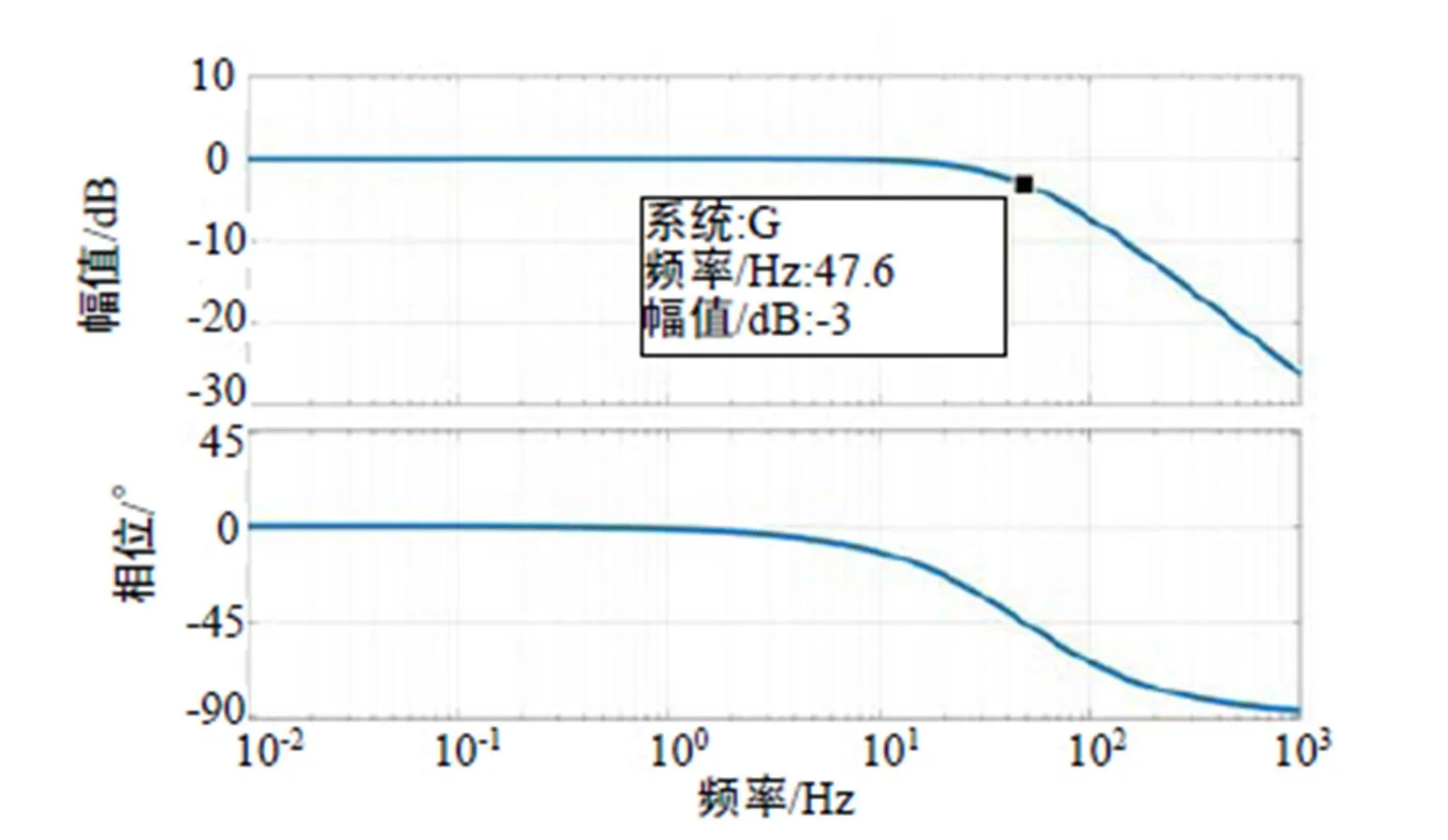
图4 ESO 伯德图
3 仿真与实验验证
3.1 仿真结果与分析
图5为本文提出的高频方波注入方法的控制框图。采用Matlab/simulink对该方法进行了仿真验证。根据理论分析,方波信号注入在轴或轴都可以估计转子位置,仿真采用注入轴来进行算法验证。仿真模型采用的电机参数和实际电机参数一致,见表1。仿真实验采用的开关频率均为5kHz,注入信号频率选取为开关频率的一半即2.5kHz,注入信号的幅值为70V。

图5 无滤波器高频方波注入控制框图
注入高频方波信号在轴,仿真转速为100r/min。通过上文提出的无滤波器高频信号分离方法来得到前一采样时刻和当前采样时刻的电流响应差值,分离得到的高频信号波形如图6所示。

图6 当前时刻和前一时刻电流差值
按照上文公式中的信号处理方式,首先每隔半个周期把高频信号取反,然后通过计算消除直流偏置量I,最后标幺化消除I得到式(13)中两个正余弦信号如图7所示。
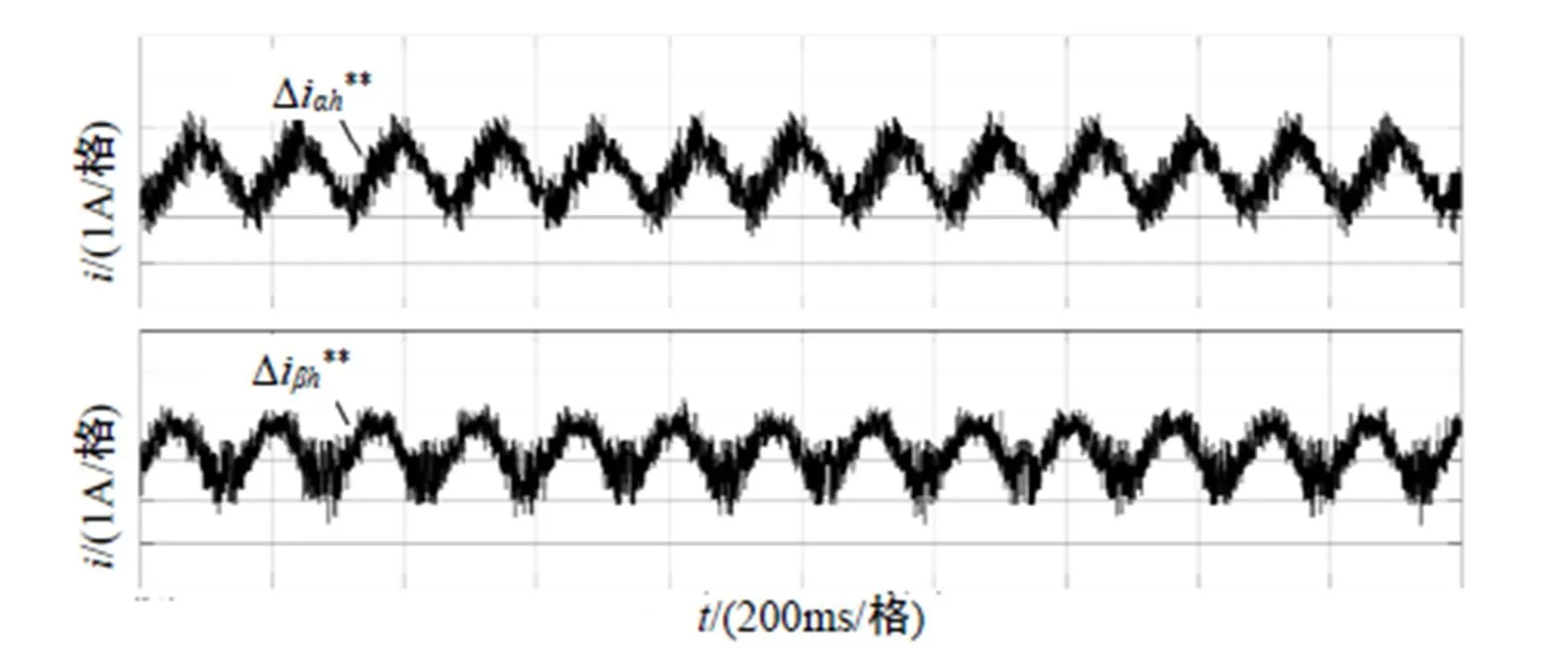
图7 当前时刻和前一时刻电流差值
得到包含转子位置信息的式(13)后把这两个信号通入转子位置观测器,得出转子角度。实际波形如图8所示。
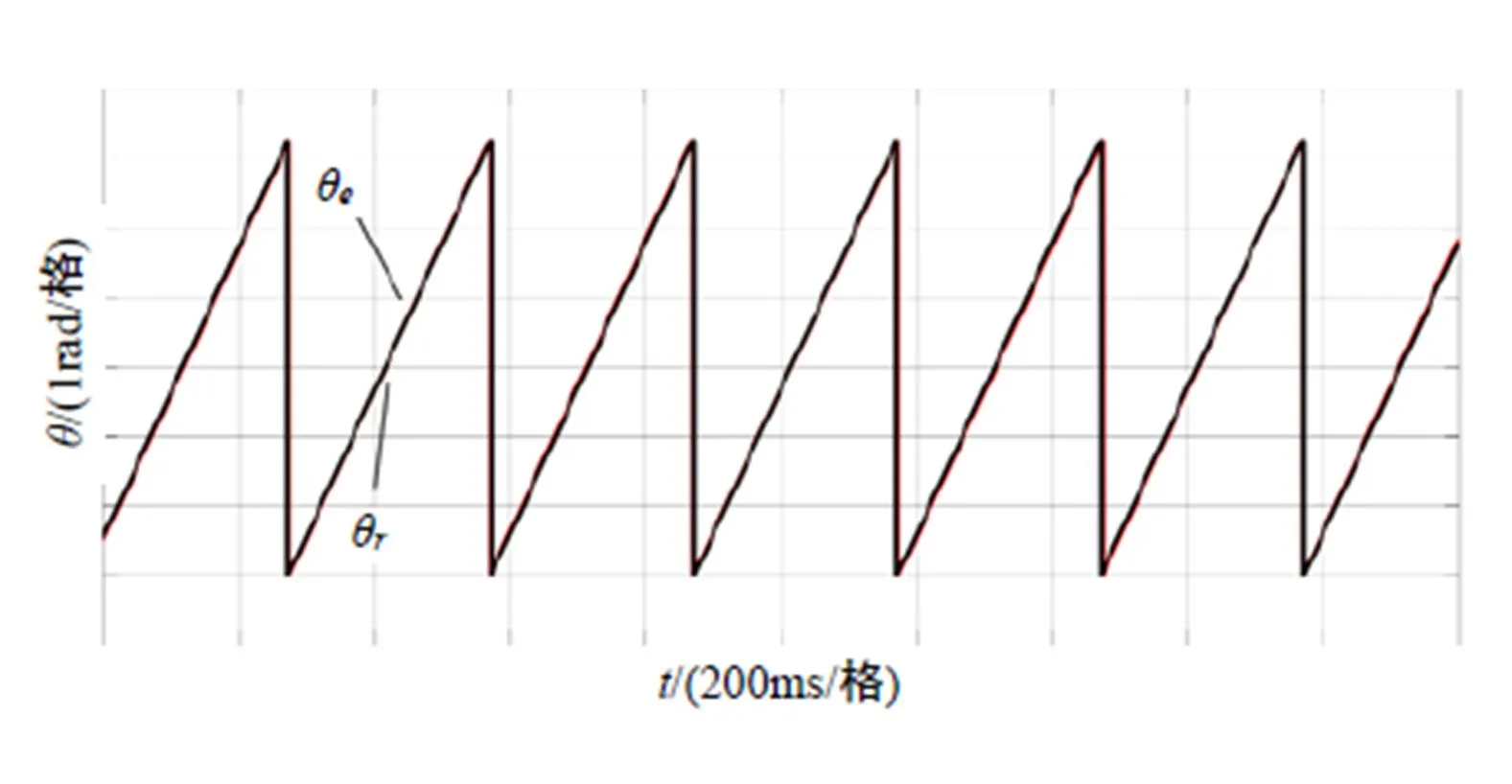
图8 转子估计角度和实际角度
本文所采用的ESO相较于PI观测器是一个更高阶的观测器,考虑了净转矩的影响,所以ESO比PI观测器抗干扰性更加强。由于实际运行中可能采样到的高频信号有噪声干扰,可能信噪比不高,这样会对转子位置估计有影响,由于ESO考虑了转矩的影响会使得估计精度更高。仿真波形上可以看出来估计的转子角度和实际角度基本重合,从而验证了算法的正确性。
3.2 实验结果与分析
采用如图9所示的实验平台对本文所提出的无传感器控制策略进行了验证。

实验在一台1.5kW的IPMSM上进行,参数如表1所示,负载转矩采用一台25N·m/2A磁粉制动器来提供,通过调节张力控制器来调节负载转矩大小,利用TMS320F2808DSP实现控制算法,采用增量式编码器PENON-K3808G获得转子实际位置,与估计位置进行对比。IPMSM电机参数如表1所示。在额定负载的条件下,采用本文提出的无位置传感器方法在不同工况下得出实验波形。
图10是电机突加突卸额定负载实验波形,此时电机运行转速为100r/min。从上至下依次为转子位置估计波形、转子位置实际波形、位置误差波形,dq轴电流波形,实际转速波形和估计转速波形。在突加负载和突卸负载的情况下,转子位置估计值能够很好地跟踪转子位置实际值,具备良好的抗扰动性能。
表1 实验电机参数
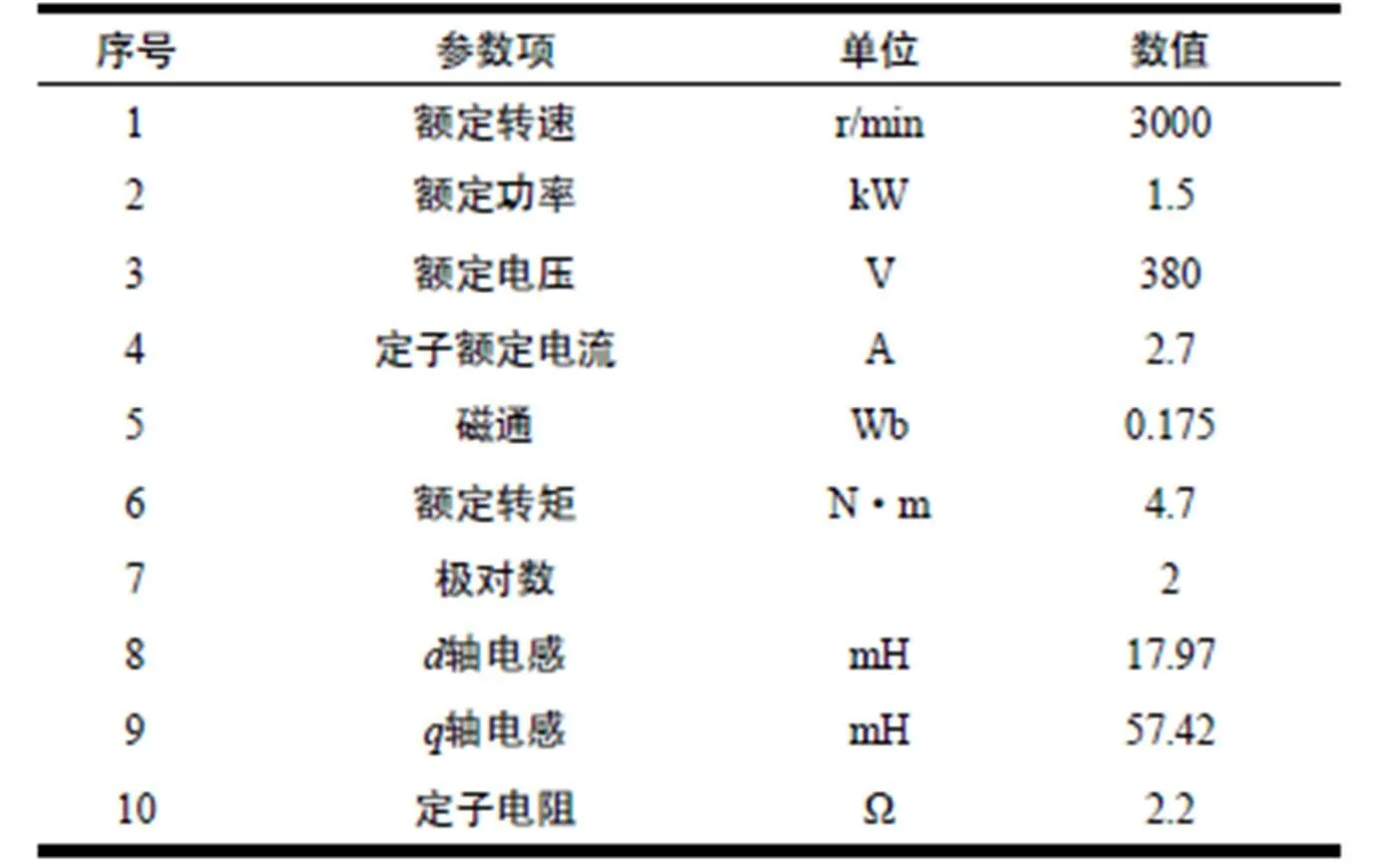
图11是电机带额定负载情况下正反转实验波形,从上至下依次为转子位置估计波形、转子位置实际波形、实际转速波形和估计转速波形、dq轴电流波形。由波形可见在该控制方法下电机能平稳地实现正反转运行,且转子位置跟踪良好。
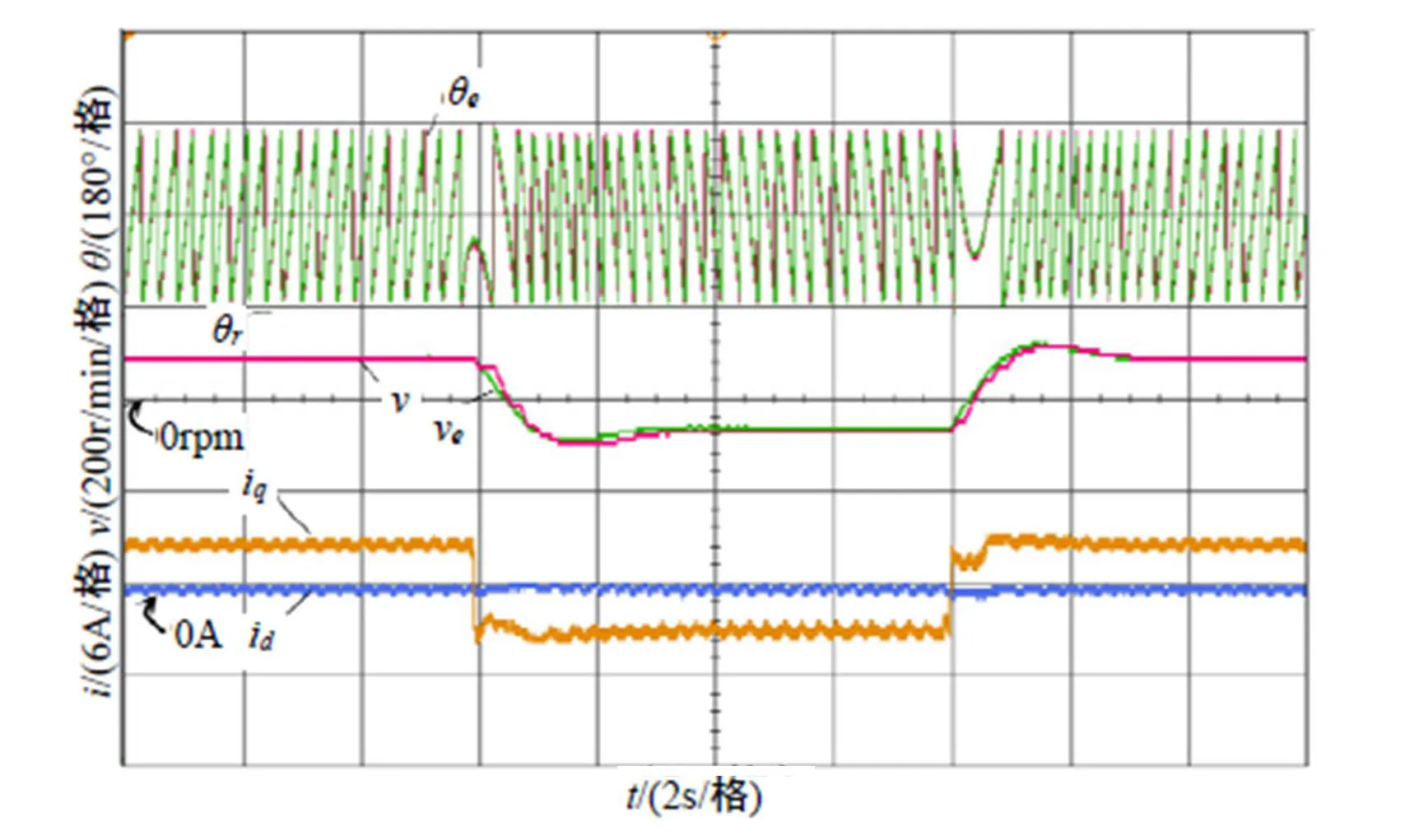
图11 正反转实验波形
4 结论
本文提出了一种基于静止参考系的高频方波电压注入的IPMSM无位置传感器控制策略,采用注入高频方波信号到()轴上的方法来获得转子位置信息,实验结果表明该方法在低速情况下有良好的性能,估计的转子位置能很好地跟踪转子实际位置,且对负载扰动有比较强的抗干扰能力。该方法方法有以下优势:
(1)整个控制算法都不需要使用滤波器,提高了控制系统的带宽,增强了响应速度;
(2)采用ESO取代PI观测器估计转子角度,增强了抗扰动能力,提高了估计精度。
[1] Y. Hua, M. Sumner, G. Asher, Q. Gao and K. Saleh. Improved sensorless control of a permanent magnet machine using fundamental pulse width modulation excitation[J]. IET Electric Power Applications, 2011, 5(4):359-370.
[2] D. Liang, J. Li and R. Qu. Sensorless Control of Permanent Magnet Synchronous Machine Based on Second-Order Sliding-Mode Observer With Online Resistance Estimation[J]. IEEE Transactions on Industry Applications, 2017, 53(4):3672-3682.
[3] 刘计龙,肖飞,沈洋,麦志勤,李超然.永磁同步电机无位置传感器控制技术研究综述[J].电工技术学报,2017, 32(16):76-88
[4] Y. Zhao, W. Qiao and L. Wu. Improved Rotor Position and Speed Estimators for Sensorless Control of Interior Permanent-Magnet Synchronous Machines[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(3):627-639.
[5] M. S. Rafaq, F. Mwasilu, J. Kim, H. H. Choi and J. W. Jung. Online Parameter Identification for Model-Based Sensorless Control of Interior Permanent Magnet Synchronous Machine[J]. IEEE Transactions on Power Electronics, 2017, 32(6):4631-4643.
[6] T. C. Lin, Z. Q. Zhu and J. M. Liu. Improved Rotor Position Estimation in Sensorless-Controlled Permanent-Magnet Synchronous Machines Having Asymmetric-EMF With Harmonic Compensation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10):6131-6139.
[7] 王高林,杨荣峰,李刚,等.基于高频信号注入的IPMSM无位置传感器控制策略[J].电工技术学报,2012, 27(11):62-68.
[8] P. L. Xu and Z. Q. Zhu. Novel Square-Wave Signal Injection Method Using Zero-Sequence Voltage for Sensorless Control of PMSM Drives[J]. IEEE Transactions on Industrial Electronics, 2016, 63(12):7444-7454.
[9] Y. D. Yoon, S. K. Sul, S. Morimoto and K. Ide. High-Bandwidth Sensorless Algorithm for AC Machines Based on Square-Wave-Type Voltage Injection[J]. IEEE Transactions on Industry Applications, 2011, 47(3):1361-1370.
[10] J. M. Liu and Z. Q. Zhu. Sensorless Control Strategy by Square-Waveform High-Frequency Pulsating Signal Injection Into Stationary Reference Frame[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2):171-180.
[11] 陈坤,王辉,吴轩,黄守道,邵俊波.一种新型的内置式永磁同步电机无位置传感器低速控制策略[J].中国电机工程学报, 2017, 37(20):6083-6091.
[12] X. Jin, R. Ni, W. Chen, F. Blaabjerg and D. G. Xu. High Frequency Voltage Injection Methods and Observer Design for Initial Position Detection of Permanent Magnet Synchronous Machines[J]. IEEE Transactions on Power Electronics, 2017, 99(1):1.
A Position Sensorless Control Strategy of IPMSM Based on Filterless High Frequency Signal Injection
FURuixiao, HUANGShoudao,WANGHailong, WANG Jiabao
(Hunan University, Changsha 410000, China)
A high frequency square wave voltage injection method based on stationary reference frame is proposed. By injecting the high-frequency square-waveform voltage into the- (or-) axis of the stationary reference frame, and the rotor position is calculated by the response high-frequency carrier current. The method greatly increases the injection frequency and can completely reduce the effects of rotor resistance. This method can avoid the use of filter, hence greatly increase control system bandwidth. Extended state observer (ESO) is also used to estimate rotor position and improve the accuracy of position estimation, and anti-disturbance ability. The experimental results demonstrated the feasibility of the proposed sensorless strategy by a 1.5kW IPMSM.
IPMSM;position sensorless;high-frequency injection;low speed; ESO
TM351
A
1000-3983(2018)06-0006-06
湖南省自然科学基金资助项目(2018JJ3057)
2018-02-10
傅睿潇(1994-),现为湖南大学电气工程全日制硕士研究生,研究方向为电机控制。


