MGP系统为新能源电网提供惯性的实验研究
周莹坤,许国瑞,黄永章
MGP系统为新能源电网提供惯性的实验研究
周莹坤,许国瑞,黄永章
(新能源电力系统国家重点实验室(华北电力大学),北京 102206)
随着电网中新能源的渗透率不断增加,电网的整体惯性不断降低,这将威胁到电网频率稳定性。同步电机对(Motor-Generator Pair, MGP)系统可以有效解决该问题。本文首先介绍了新能源电网的惯性特性,随后介绍了MGP系统的基本概念,基于MGP系统的功率相位关系提出源网相位控制方法,最后通过实验比较了光伏系统有无MGP系统时的频率响应情况。实验结果表明,MGP系统可以为新能源提供惯性支持,这将提高新能源电网的频率稳定性。
高新能源渗透率;电网惯性;同步电机对系统;频率稳定性
0 前言
为了保护全球环境,降低化石能源比例,使用新能源发电替换传统火力发电厂,提高新能源的比例是一个重要手段,高渗透率新能源电力系统是未来电力系统发展的大趋势[1]。然而,新能源的快速发展也带来了一些新的挑战。新能源发电一般通过电力电子变换器接入电网,与传统的并网方式(如火电机组)相比,这种方法具有控制快速灵活的特点,但也存在着非线性和惯性不足的缺陷。随着新能源发电的不断渗透,电网中将出现大量并网型电力电子逆变器。相反,传统同步发电机的比例会降低,从而降低电网的旋转备用容量和转动惯量,进而危及电网的频率稳定性[2]。
为了应对新能源发电带来的冲击和挑战,大批学者对并网逆变器的改进控制开展了研究[3]。文献[4]对风场的等效惯性时间常数进行了分析。文献[5]为了使逆变器模拟同步发电机频率调节能力,支撑电网稳定性,提出了虚拟惯性控制策略。文献[6]提出了虚拟同步发电机(VSG)方案,在外特性上模拟了同步发电机摇摆方程。文献[7]提出的虚拟同步电机(VISMA),可以使逆变器体现同步发电机的惯性特性,更好地为系统提供频率支撑。文献[8]和[9],基于同步发电机的机电暂态模型,在频率控制上模拟同步发电机的转子惯量与系统调频特性,在电压控制上,考虑无功-电压关系,以控制电压稳定输出。文献[10]综合考虑到同步发电机的机电暂态和电磁暂态特性,提出了基于同步发电机交流侧动态模型的同步逆变器,实现了同步发电机和逆变器在物理与数学模型上的等效及VSG的自同步运行。文献[11]提出采用双馈发电机的抽水蓄能电站的虚拟惯性控制,利用双馈机组转速可调的特性调节瞬时功率,但是在水源不足的新能源电场,该方法并不适用。
现有的改进都着眼于逆变器的控制策略上,但是上述控制改进方法并不能从根本上改变电力电子逆变器的缺陷。对于光伏发电,要进行虚拟惯性控制必须额外配置储能环节,其成本分析尚未见报道。
文献[12]~[14]提出了一种新的思路,通过同步电动机-同步发电机对(MGP)系统并网来改善新能源并网时的惯性。逆变器不直接连接到电网,而是通过逆变器-同步电动机-同步发电机的方式并网。这种方法可以利用同步发电机固有的惯性来提高新能源并网的惯性。而且,同步发电机的控制系统可以完全遵循现有的火电机组的同步发电机控制,这将极大地提高电网的稳定性,减少了新能源对电网的冲击。
本文首先介绍了MGP系统的工作原理和它能提供的惯性大小。然后,分析了MGP系统有功功率和源网相位差的对应关系,提出了源网相位控制方法的理论基础。基于上述分析,以一个2kW的并网系统为例,通过实验,比较了光伏系统有/无MGP系统时的频率响应情况。实验结果表明,MGP系统可以为新能源提供惯性支持,增强新能源电网的频率稳定性。
1 同步电机与逆变器的惯性分析
同步发电机的惯性可以用转动惯量或惯性时间常数表示。由于逆变器不包含直接转动惯量,所以描述新能源的惯性时,用惯性时间常数来表示。
对于同步电机,其转子动能M可以表示为:
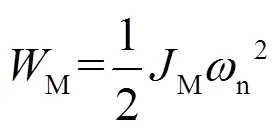
其中,M是转子转动惯量,n是电机转速。这里默认电机为一对极。
同步电机的惯性大小可以用惯性时间常数进行表示,其表达式为:

其中,Ng是同步发电机的额定容量。
新能源包括风电和光伏等,现在都使用逆变器并网。逆变器的惯性来自逆变器直流侧电容储存的能量。逆变器的惯性时间常数C为:

其中,为逆变器直流侧电容,C为逆变器直流侧电压,一般在450~800V范围内。Nij为新能源额定容量。对于由个单元并联组成的新能源电场,它的惯性时间常数C'为:

这里假设同一新能源电场内,所有机组都有相同的惯性时间常数,则C'=C。
假定一台900MW的同步发电机惯性时间常数M为6.5s[15]。对于一个包含450台2MW风力发电机的900MW风电场,取C的平均值为625V,=0.1F,该900MW风力发电场的惯性时间常数为0.016s,M/C'=406.25。由此可知,新能源机组大规模接入电网将大大降低电网的惯性。
2 MGP系统基本特性
MGP系统的原理如图1所示。在新能源电场的末端,增加了一组由同步电动机和同步发电机组成的电机对,然后并到电网中。考虑到新能源电场的总容量通常达到兆瓦级,普通直流电机和感应电机很难做到这一点,而同步发电机的现有容量可以达到几百兆瓦,所以发电机和电动机都设计为同步电机。

图1 MGP原理图
对于MGP系统,其转子惯性是由转子质量和转子转速决定的。当MGP系统运行时,其惯性可以近似为一个常数,通过计算可知,其惯性的大小约为同容量火电机组惯性的65%[15]。
因为MGP的两台同步机同轴连接,可以假定两台电机的转速和转速变化均相同,而且两台电机转子的稳态机械转矩也相同。所以可以假定两台电机使用各自的电磁方程和电磁转矩,使用同一机械系统。假定两台电机的惯性时间常数为G,M,电磁转矩为eG,eM,转子角为G,M,阻尼系数是DG,DM,得到:
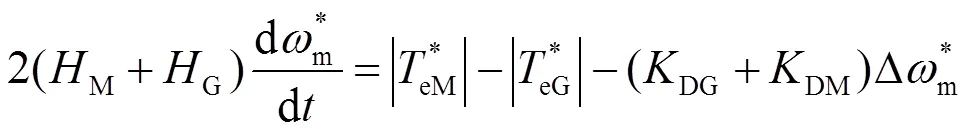
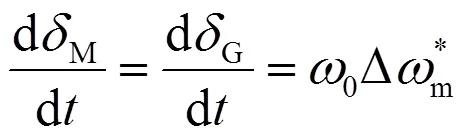
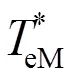
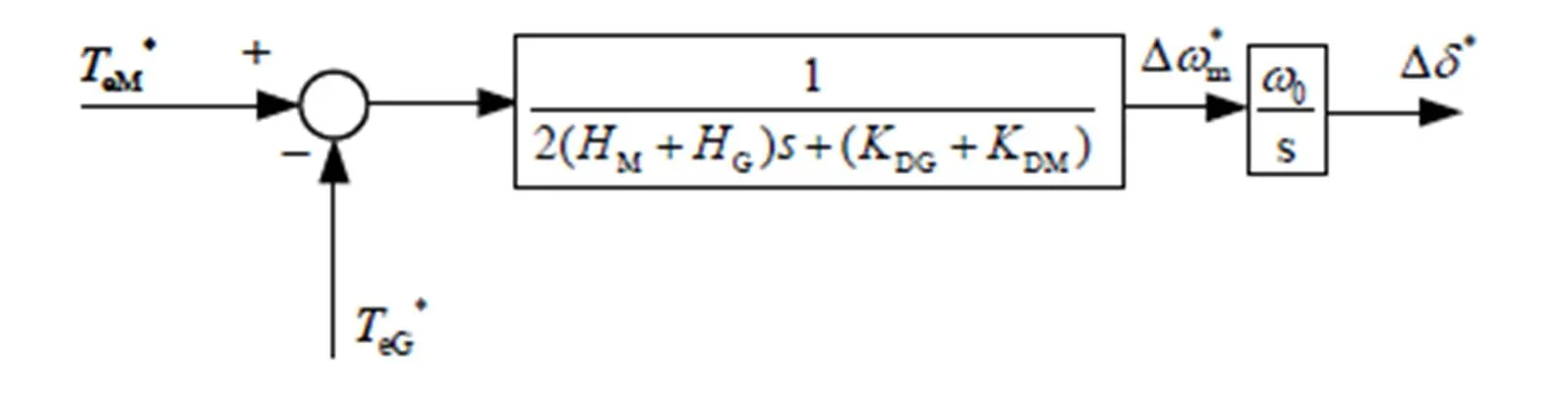
图2 MGP系统机械模型框图
在上述分析的基础上可得MGP系统模型图如图3所示,其中source和grid是电动机和发电机的端电压;source,grid是电动机和发电机定子电流;Δm,ΔG是电动机和发电机的转子角度的变化;Δ是转子转速变化。发电机和电动机各自有一套电磁系统,可以计算机械系统输入的电磁转矩。进而可以计算MGP系统转子转速和转子位置。两台电机的转速和转子位置相同。同时,转子的位置和转速是两机电气部分的输入,参与电磁转矩的计算。

图3 MGP系统建模结构
3 MGP系统功角特性与控制方法
(1)MGP转子角与功率变化对应关系
对于同步电动机,通过它传输的有功功率可以简化为(7)式:

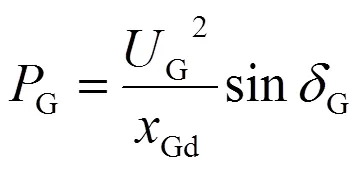
其中,G是发电机机端电压,Gd是发电机定子d轴电抗,G是发电机转子角。
MGP系统的功率变化和转子角之间的对应关系如图4所示(假设物理位置上两个转子之间的角度差为0,因为两台电机的转子轴是耦合的)。如图5所示,通过实验可以得到MGP系统传输的有功功率和其两端电压差的对应关系。

图4 MGP转子角关系

图5 调节新能源和电网相位角时有功功率曲线
(1)控制方法
根据上文分析所得MGP系统两台同步电机的功角特性,可以采用如图6(a)所示,通过采集电网频率作为变频器的输出电压频率的参考值,然后直接改变相位差来控制功率传输。反馈系统的算法如图6(b)所示,测量电网电压(发电机侧)的频率与相位电压,传输功率可以通过调节发电机端电压和电动机端电压相位差来控制。
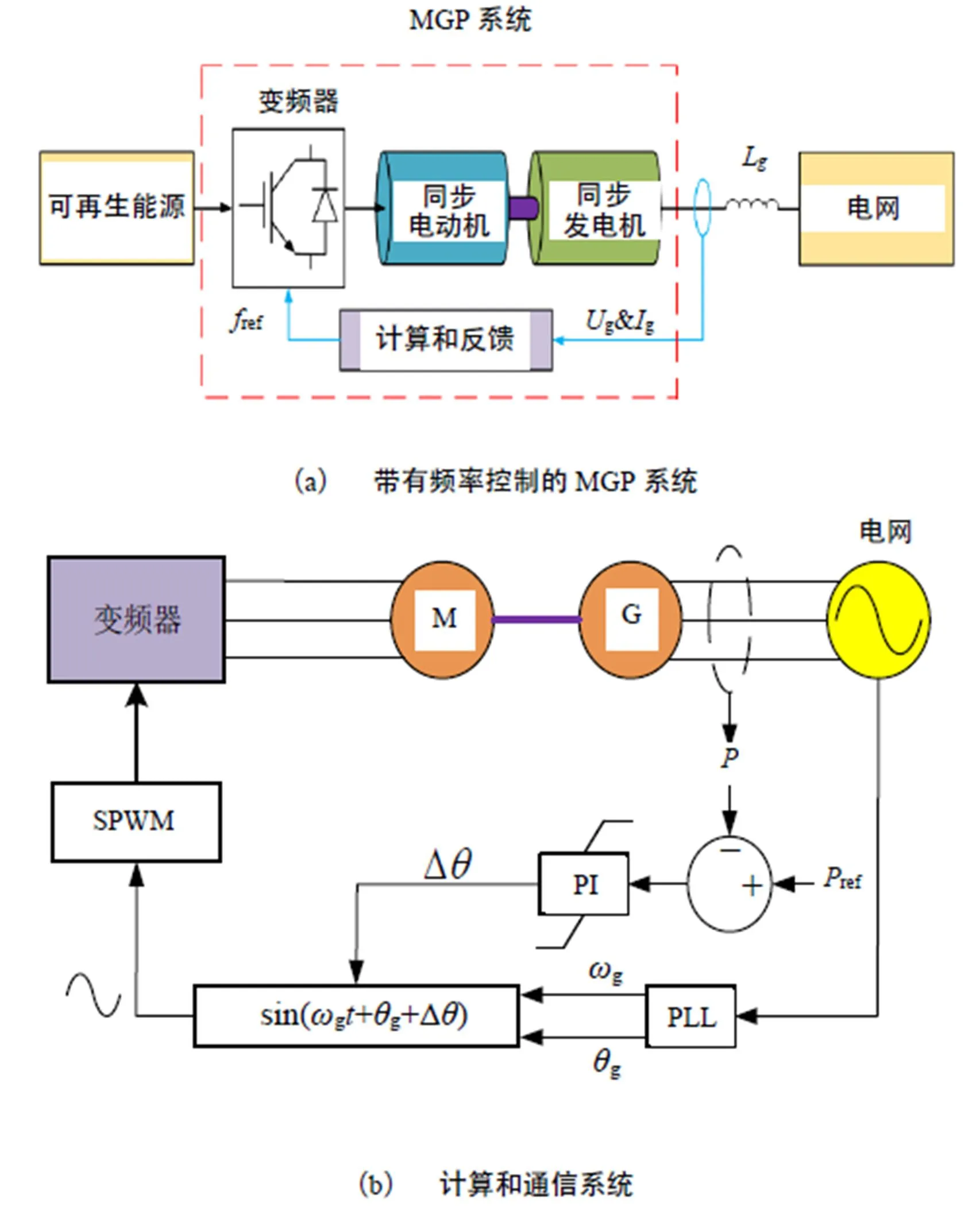
图6 MGP系统频率反馈控制框图
图中:
g:电机机端电压
g:发电机输出电流
g:输电线路等效电抗
:MGP系统输出有功功率
G:频率调整模块(使用PI控制)
Δ:频率调节量
ref:MGP系统输出有功功率参考值
g:电网电压的角频率
g:电网电压相位
grid:电网电压频率
ref:变频器输出电压的频率参考值
Δ:相位调整量
直接采集频率反馈调节相位控制有功的方法,对于设备的测量精度要求非常高。在仿真中可以轻易实现的控制方法,在实验中由于设备精度的限制,并不容易实现。但是通过调节变频器输出电压的频率,也可以改变MGP系统两端电压的相位差。由此可以考虑将相位从直接调节量改为间接调节量,以避免控制系统对于频率敏感度过大的问题。
基于上述分析,本文提出如图7所示的功率反馈控制系统。测量计算系统检测发电机向电网发出的实际有功与有功给定值之间的差,通过PI调节计算出频率调节量并以此作为反馈,在控制系统中计算变频器频率参考值,对变频器频率进行微调,通过调频来调节相位差,进而控制功率输出。

图7 基于功率反馈的改进控制方式
4 MGP系统惯性支撑能力实验分析
为了证实MGP系统的惯性支持能力,此处开展了如下对比实验。在设定源端功率波动时,分析光伏系统带有/不带有MGP系统时,新能源输出端口电压的频率响应情况。实验系统如图8所示。

图8 实验系统
如图8所示,两台2kW的同步电机分别作为同步电动机和同步发电机。使用调压器加整流器作为同步电机的励磁系统,30kW的变频器用来驱动电动机。使用录波仪(横河DL850)用来测量发电机传送到电网的功率以及并网点电压频率,PLC用于计算和通信。光伏发电系统(PV)由一个直流电源(IT6726V)和一台逆变器模拟。详细实验参数见表1和表2。
表1 实验中电机的部分参数

表2 光伏系统和MGP的实验参数
(1)带负载实验
实验步骤:
1)打开K4,通过变频器启动电动机直到MGP达到同步速。然后,闭合K1,K3,将MGP系统和负载连接。
2)设定负载值为1200W。
3)将负载值从1200W变为0W,观察MGP系统输出电压(母线电压)的频率变化。
4)将负载值从0W变为1200W,观察MGP系统输出电压(母线电压)的频率变化。
5)将MGP系统并网变为PV系统,重复上述实验。
在实验进行到大约3.2s时,设定负载突变,MGP系统和PV系统的有功功率也会随之变化,此处测量母线电压的频率变化过程,实验结果如图9所示。从实验结果可以看出,母线电压的频率随着负荷的减小/增加而增加/降低。通过对比可以看出,在负荷突减,频率突增的过程中,MGP系统可以将PV系统的输出电压的频率波动最大值减少一倍以上,MGP系统的频率波动明显低于光伏系统。同时从对比结果还可以看出,MGP系统的动态恢复过程更快。这些结果表明MGP系统能为新能源提供惯性支持,增强新能源电网的频率稳定性。

图9 带负载实验母线电压频率
(2)并网实验
实验步骤:
1)打开K3,通过变频器启动电动机直到MGP达到同步速。启动图6(b)所示控制系统控制功率传输,利用暗灯法,闭合K2,K4将发电机并网。
2)设置发电机的功率参考值为1200W,调节比例系数直到系统稳定。
3)将有功参考值从1200W降低到0W,观察MGP系统向电网传输功率和母线电压频率的变化。
4)将MGP系统变为PV系统并网,重复上述实验。其中输出功率可以通过直流电源输出电压控制。
实验结果如图10所示。由于g的存在,可以看出,有功功率降低的同时,母线电压频率也随之降低。从比较结果来看,MGP系统可以将PV系统的输出电压的频率波动最大值减少接近一倍,可见MGP系统的频率波动明显小于光伏系统,MGP系统的动态恢复过程也更快。这些实验现象与带载实验的结果相似。这些结果同样表明MGP系统能为新能源提供惯性支持,增强新能源电网的频率稳定性。
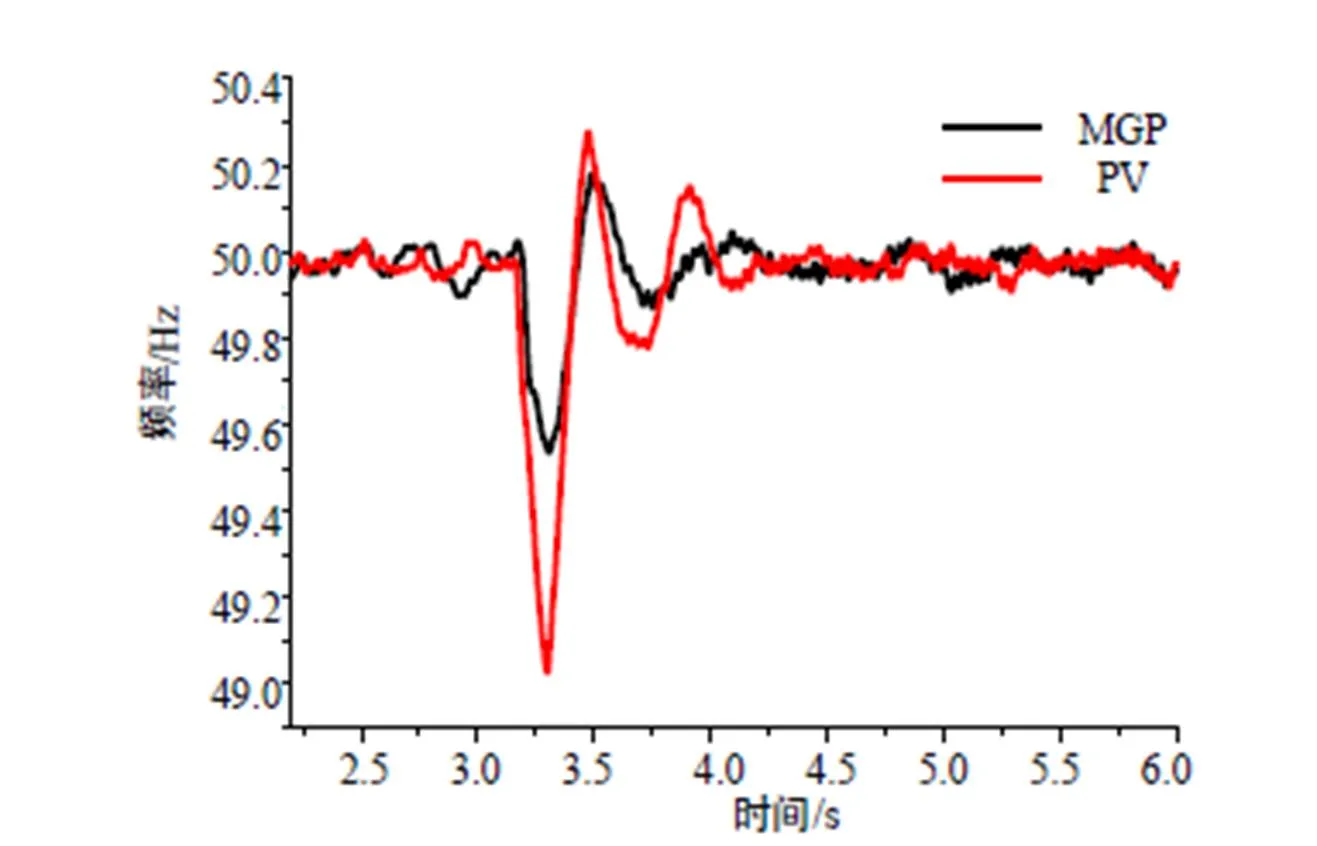
图10 并网实验母线电压频率
5 结论
本文分析了当前能源和环境现状,阐述了建设高渗透可再生能源电网的必要性。然后分析了新能源高渗透率下给电网带来的潜在问题。讨论了这些问题的解决方案—MGP系统,并用实验分析了其惯性,得出结论如下:
(1)提出了MGP系统的数学模型。根据该数学模型,建立了源电网相位差和MGP系统的有功功率的对应关系;
(2)对比实验结果表明MGP系统能够为新能源提供惯性支持,增强新能源电网的频率稳定性。
[1] Lasseter, R. H. Microgrids and distributed generation[J].Journal of Energy Engineering,2007, 133(3): 144-149.
[2] Heydt, Gerald Thomas. The next generation of power distribution systems[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 225-235.
[3] Soni, Nimish, Suryanarayana Doolla, and Mukul C. Chandorkar. Improvement of transient response in microgrids using virtual inertia[J]. IEEE Transactions on Power Delivery, 2013, 28(3): 1830-1838.
[4] 李世春, 邓长虹, 龙志君, 周沁, 郑峰. 风电场等效虚拟惯性时间常数计算[J]. 电力系统自动化, 2016, 40(07):22-29.
[5] Xiang-Zhen, Yang. Control strategy for virtual synchronous generator in microgrid[C].Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), 2011 4th International Conference on. IEEE, 2011.
[6] Visscher, K., and S. W. H. De Haan. Virtual synchronous machines (VSG’s) for frequency stabilisation in future grids with a significant share of decentralized generation[C].CIRED Seminar 2008: SmartGrids for Distribution. 2008.
[7] Beck, Hans-Peter, and Ralf Hesse. Virtual synchronous machine[C].2007 9th International Conference on Electrical Power Quality and Utilisation. IEEE, 2007.
[8] Shintai, Toshinobu, Yushi Miura, and Toshifumi Ise. Oscillation damping of a distributed generator using a virtual synchronous generator[J]. IEEE Transactions on Power Delivery, 2014, 29(2): 668-676.
[9] Alipoor, Jaber, Yushi Miura, and Toshifumi Ise. Power system stabilization using virtual synchronous generator with alternating moment of inertia[J].IEEE Journal of Emerging and Selected Topics in Power Electronics 2015,3(2): 451-458.
[10] Zhong, Qing-Chang, and George Weiss. Synchronverters: Inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[11] 李辉, 刘海涛, 宋二兵, 肖洪伟, 骆林, 黄智欣. 双馈抽水蓄能机组参与电网调频的改进虚拟惯性控制策略[J]. 电力系统自动化,2017,41(10):58-65.
[12] Wei S., Zhou Y., Xu G., & Huang, Y. Motor-generator pair: a novel solution to provide inertia and damping for power system with high penetration of renewable energy[J]. Iet Generation Transmission& Distribution. 2017, 11(7): 1839-1847.
[13] Wei, S. Zhou,Y. Li,S. and Huang ,Y. A possible configuration with motor-generator pair for renewable energy integration[J]. CSEE Journal of Power and Energy Systems, 2017, 3(1): 93-100.
[14] 卫思明, 黄永章. 风电采用MGP并网的小干扰建模和阻尼特性[J]. 电力系统自动化, 2017, 41(22): 16-25.
[15] Kundur, Prabha.Power system stability and control. Eds. Neal J. Balu, and Mark G. Lauby. Vol. 7. New York: McGraw-hill, 1994.
Experiment Analysis on Motor-Generator Pair System for Providing Inertia for Power System with Renewable Energy
ZHOU Yingkun, XU Guorui, HUANG Yongzhang
(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources (North China Electric Power University), Beijing 102206, China)
With the increasing of penetration of renewable energy, the whole inertia of the power system is declining, which will endanger the frequency stability. Motor-Generator Pair (MGP) system can deal with these problems efficiently. In this paper, the basic working principle of MGP system is introduced firstly, then the theoretical basis of source-grid phase control method is proposed. The frequency response of PV system with/without MGP system is compared by experiment. The results show that the MGP system can provide inertia support for renewable energy, which can increase frequency stability for renewable energy power grid.
high renewable energy penetration; inertia of power grid; Motor-Generator Pair system; frequency stability
TM341
A
1000-3983(2018)06-0012-06
国家电网公司科技项目(5201011600TS)国家电网公司科技项目(XT71-18-041)
2017-12-16
周莹坤(1990-),华北电力大学。电气与电子工程学院,电气与通信工程专业,博士研究生在读,主要研究方向为高渗透率新能源电力系统稳定性。


