静止状态下的多相感应电机参数辨识方法
郑仕达,杨家强
静止状态下的多相感应电机参数辨识方法
郑仕达,杨家强
(浙江大学,杭州 310027)
在多相感应电机非对称T型等效电路的基础上,提出了一种静止状态下的参数辨识方法。考虑到低压大功率多相感应电机的参数较常规三相感应电机小,为避免逆变器非线性和补偿误差,采用直接测量相电压的方法代替电压重构法,可以准确辨识出电机的全部参数。针对励磁电感在数值上仅为几毫亨,对采样误差较为敏感的问题,励磁电感的辨识采用低频交流注入和突减电流两种方法互相校核。最后通过实验验证了该方法的有效性。
参数辨识;静止状态;低压大功率;多相感应电机
0 前言
多相电机相比三相电机具有更小的转矩脉动、更好的容错控制性能,在电压受限的场合可以实现低压大功率[1,2],越来越多地在工业控制、交通运输等领域得到应用,前景广阔[3]。
与三相电机控制相似,多相感应电机的矢量控制等高性能算法需要在磁链、速度的观测上获得准确的参数,以确保电机的运行性能。传统的参数辨识方式通过空载和堵转实验获得[4],但是对于已经安装到机电系统上,负载难以脱除的电机,传统的空载、堵转实验无法实现。因此有必要对静止状态下的电机参数辨识进行研究。
本文的研究对象为电动汽车用的七相感应电机,专门为低压大功率场合定制。较一般三相电机而言,在相同磁通条件下,每相等效串联匝数很小,故待辨识的励磁电感很小(约几毫亨),采用文献[5]的方法用对直流母线电压重构后的电压作为相电压,需要补偿IGBT和二极管的压降,补偿的准确性较差。故针对这类励磁电感较小的多相电机,本文增加了一个电压传感器直接获得相电压值,辨识静止状态下的定转子电阻、漏感、励磁电感参数,针对较小的励磁电感,采用低频交流注入和突减电流两种方法来互相校核。最后,电机参数的辨识结果与解析解和有限元仿真解进行对比,验证了方法的有效性。
1 多相感应电机参数辨识模型
非对称T型等效电路(也称反Г型等效电路)常用于各种电机控制算法中,如图1所示。
u、i分别为电机相电压和相电流;u、i分别为励磁绕组端电压和励磁电流;R为定子电阻,为漏感,为转子电阻,为励磁电感。其中转子电阻已折算到定子侧,、考虑其磁饱和等非线性因素,分别与定子电流i和励磁电流i有关,可以表示为(i)、(i)[6]。
本文对七相感应电机参数辨识的依据就是图1模型。首先进行定子电阻和漏感的辨识,接下来利用定子电阻和漏感的值,完成转子电阻和励磁电感的辨识。

图1 感应电机非对称T型等效电路
2 定子电阻和漏感的辨识
2.1 直流伏安法辨识定子电阻
定子电阻一般采用直流伏安法获得,通过电流闭环控制,使某相中通入给定直流电流,此时电机内部不产生旋转磁场,电机处于静止状态。通过电压传感器获得相的电压和电流传感器获得的相电流,可以计算得到定子电阻为:
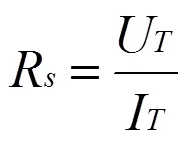
式中,和分别为相绕组上的直流电压和相电流。由于电压传感器直接测量相电压,故逆变器的非线性因素无需考虑。
2.2 高频注入法辨识漏感

图2 感应电机漏感辨识的交流等效电路
向绕组中注入给定电流波形,测得相绕组两端电压波形:
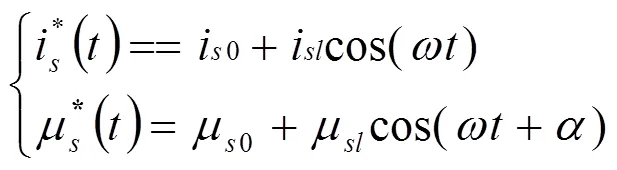
式中,()为给定电流,包含了i0直流偏置分量和icos()的交流小信号,u()为绕组两端的电压,包含了u0直流偏置分量和ucos()的交流小信号。则漏感可以直接由下式计算得到:
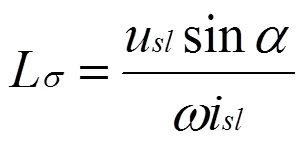
由于这种方法计算出来的漏感,包括之后辨识的励磁电感,均为瞬态电感[8](记为(ins)),是实际工作点P附近磁链关于电流的微分d/d:
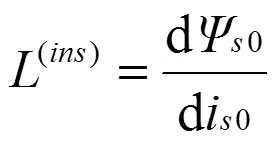
对瞬态电感关于电流积分,得到磁链-电流曲线,如图3所示:
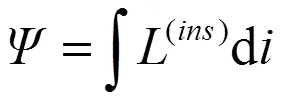
实际应用中,对于某一个磁路工作点=(i0,Ψ0),静态电感(act)可以由式(6)得到。


图3 磁链-电流曲线上的瞬态电感和静态电感
值得一提的是,公式(2)中的ucosα/i并不能得到真正意义上的转子电阻。因为电机在正常运行状态下转子电流频率很小,为转差频率,但漏感辨识实验中通入的交流量频率较高,这样运算得到的是高频转子电阻,无法在控制中使用,需要进一步辨识。
3 转子电阻和励磁电感的辨识
3.1 交流注入法辨识转子电阻
转子电阻的辨识方法与漏感相似,都是向相绕组中通入含交流小信号的直流分量*()=i0+icos(ωt),直流电流用于选定稳态工作点,交流小信号幅值很小。考虑到转子电流在电机运行过程中与定子电流存在转差频率的频率差,静止状态下转子固定,为准确得到不同转差率下的转子电阻,交流小信号频率设定为使转差率从0.1开始一直到1的值。在这样的输入条件下,参数辨识的等效电路与图1相同。于是有:
u=u-i(R+jωL) (7)
且:
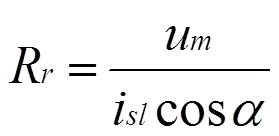
上两式中,u为图1等效电路中励磁绕组两端电压幅值,u和i分别为相绕组上的电压和电流的交流分量幅值,R和L为前文方法辨识获得的参数,为u和i之间的相位角。通过对采集到的电压电流数据进行FFT分析,取出基波分量,计算出相位角,便可以通过式(8)得到转子电阻的辨识值。
3.2 低频注入法辨识励磁电感
基于转子电阻辨识的方法,将交流小信号的频率设置为额定转差频率ω0,本文中选取ω0=1Hz,改变相电流大小进行辨识实验。由于定子电阻和漏感已经辨识得到,那么励磁电感也可以类似得到:

与漏感相同,式(9)计算出来的电感也是瞬态电感,实际应用中,需要将励磁电感关于电流积分,在磁链-电流曲线上计算静态电感。
3.3 突减电流法辨识励磁电感
对于每相串联匝数小、电压低、频率高的电机,励磁电感非常小。为减小辨识误差,本文额外采用突减电流法来与低频注入法的结果进行比对校验。
众所周知,对于定子线圈而言,定子自感等于自感磁链与其励磁电流的比值,也可以写为:
Ψ=Li(10)
向相绕组中通入直流电流i,静止状态下转子中没有感应电流,电机内的磁链全为定子磁链。考虑到反电势为磁链的变化率,改写为积分形式如下:

上式中,Ψ(0)为直流激励下的稳态磁链。当突减电流给定为0,电流i()会随着时间迅速减小,电压u()会受到定子自感反电势的影响产生一个负向的电压脉冲。当i()和u()同为零时,式(11)中(u()-Ri())所代表的反电势项为0,此时为1时刻,定子磁链Ψ(1)=0。即稳态定子磁链可以通过式(12)计算得到:
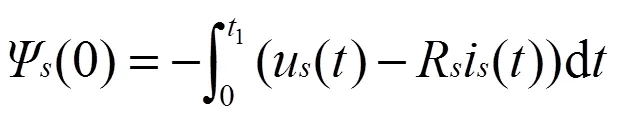
从电流给定为0开始,一直积分到电压电流均小于A/D采样的分辨率,计算得到稳态定子磁链,根据式(13)即获得励磁电感。
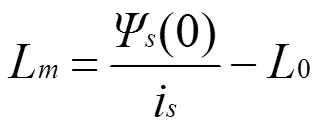
4 实验结果及其分析
验证本文方法的多相感应电机基本数据见表1,采用基于Speedgoat高性能实时目标机的多相电机控制柜完成整个静止状态下的参数辨识,实验平台如图4所示。
表1 七相感应电机基本数据

参数辨识实验采用电流闭环控制,在定子电阻的辨识实验中,每个电流值计算5次,取平均值作为该电流下的定子电阻辨识值。
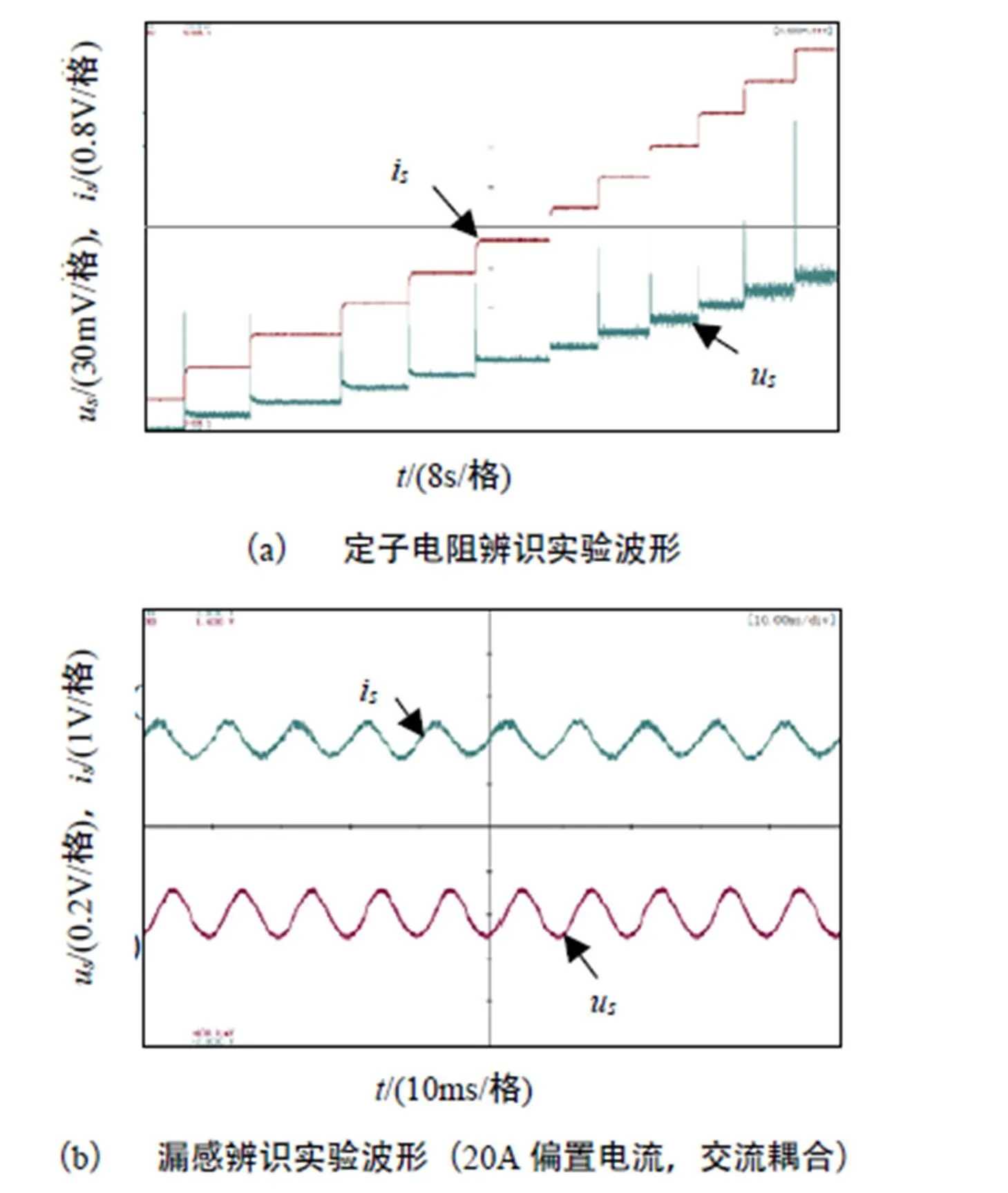
在漏感的辨识实验中,交流小信号在10A以下时给定0.5A的幅值,其他电流下均为1A的幅值。录波仪设置为交流耦合,并且选取200kS/s的采样率,使每个周期内有2000个点可供计算。选取波形中的5个周期进行FFT分析,计算后得到漏感的辨识值。考虑到漏感与定转子相对位置有关,在不同转子位置上进行5组实验。
交流注入法和低频注入法均选取5个周期进行FFT分析,计算得到转子电阻和励磁电感的辨识值。对于突减电流法,从给定电流为0开始积分,直到电压电流均小于测量灵敏度结束,并计算出相应的励磁电感。实验波形如图5所示。
本文七相感应电机针对低压大功率电动汽车驱动场合,基于ANSYS有限元仿真软件进行电机本体设计,如图6所示。故通过实验辨识结果与有限元参数计算结果相对比,可以检验辨识方法的准确性。实验结果及对比如图7所示。
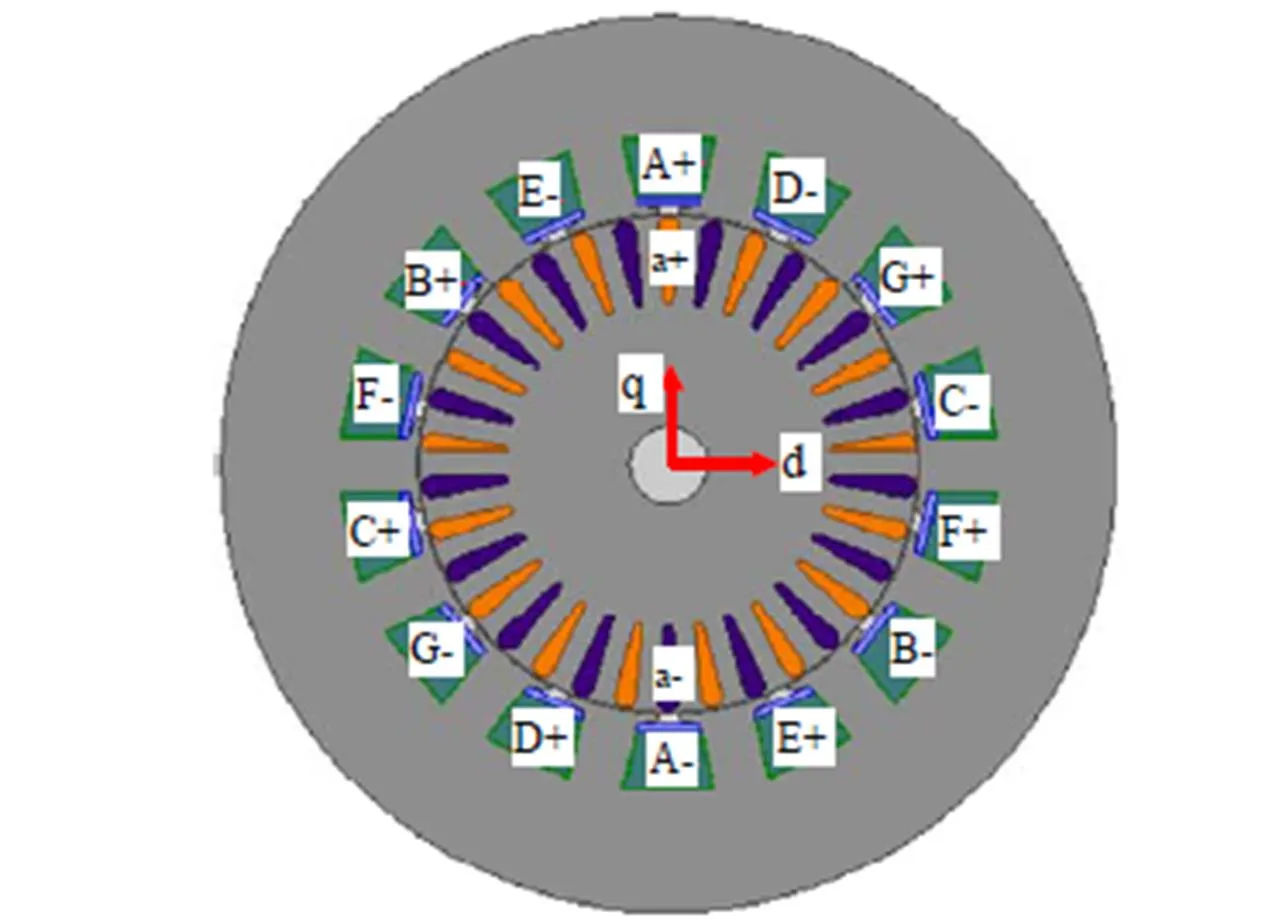
图6 七相感应电机有限元设计及计算模型
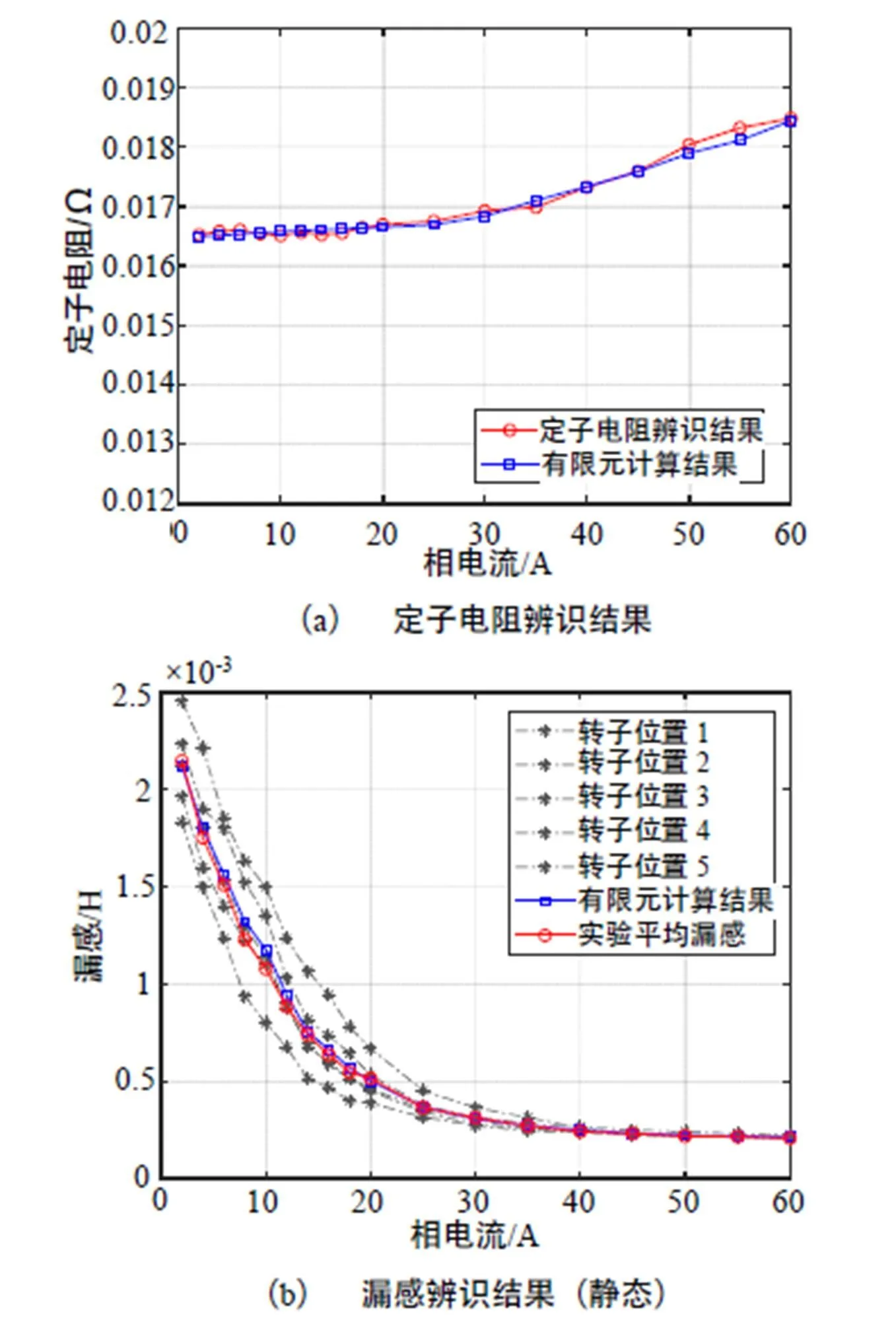
图7 七相感应电机参数辨识结果
从图7中可以得到如下结论:
(1)定子电阻随电流变化非常小,但是仍然由于发热有少量的增大。如果对电机控制性能要求较高,在电机运行过程中可以结合在线辩识算法修正定子电阻参数,提高控制性能;
(2)随着电流增大,漏感减小,并且趋于饱和,这是由于转子为闭口槽,在电流较小的情况下,磁力线大多从转子槽口形成闭合回路,漏感相对较大,在转子槽口磁密随电流增大饱和后,漏感减小,之后相对保持不变。另外,在转子位置不同的情况下,定子槽对转子槽、定子齿对转子槽所构成的磁路不同,在电流较小时对应的漏感有较大的差别。一般电机在正常运行下,定转子相对位置变化很快,漏感可以参考图7(b)的虚线,即最大与最小的平均值。极低速运行下(<10r/min)需要考虑漏感随转子位置的变化;
(3)转子电阻随转差率的增大而增大,近似呈线性关系,起动或者调速的过程中,可以对应实时的转差率选取对应位置的转子电阻,以获得更好的调速效果;
(4)图7(d)中显示了两种方法测得的励磁电感,并且与有限元计算结果相互校验。为综合考虑两种方法的计算结果,本文采用最易操作的平均值方法。可以看出平均励磁电感曲线较两种方法各自的曲线与有限元法更加吻合,且平均误差更小。
实验测得的电感参数为瞬态电感,图7中已经将电感的结果进一步表示为静态电感。
对于七相感应电机,除上述基波平面的参数外,还有三次、五次谐波平面的参数,主要体现在漏感和励磁电感上。三次和五次谐波平面的电感一般取对应基波参数的1/9和1/25。
5 结论
本文以18.5kW七相感应电机为例,设计了静止状态下参数辨识的方法。通过将实验结果与有限元计算结果相对照,本文方法能够有效并准确地辨识出多相感应电机非对称T型等效电路下的全部参数。并且低频注入法和突减电流法两种方法相互校验来辨识励磁电感,可以提高励磁电感辨识的准确性,解决了低压大功率电机因励磁电感过小而导致辨识不准的问题。最后辨识结果提供了参数随电流或转差率的变化关系,为电机在不同运行状态下的参数选择提供依据。
[1] F. Barrero, M. J. Duran. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part I[J]. IEEE Trans. Ind Electron. 2016, 63(1):449-458.
[2] 杨家强,高健,黄进. 多相感应电机指数响应电子变极方法研究[J]. 中国电机工程学报,2013,33(27):105-111.
[3] 康敏,黄进,等. 多相异步电机参数的计算与测量[J]. 中国电机工程学报,2010, 30(24): 81-87.
[4] 汤蕴璆. 电机学[M]. 北京:机械工业出版社,2008:185-187.
[5] 刘鹏,吴文进,苏建徽. 一种异步电动机静止状态下参数辨识的改进方法[J]. 电工技术学报,2015, 30(5):42-48.
[6] M. Zigliotto, M. Carraro, F. Tinazzi. The influence of the squirrel cage rotor in the estimation of the IM flux linkage at standstill[C]. IEEE International Conference on Industrial Technology,2013, 113(8):410-415.
[7] M. Carraro, M. Zigliotto. Antomatic Parameter Identification of Inverter-Fed Induction Motors at Standstill[J]. IEEE Trans. Ind. Appl, 2014, 61(9):4605-4613.
[8] L. Peretti, M. Zigliotto. Automatic procedure for induction motor parameter estimation at standstill[J].IET Electr. Power Appl., 2012, 6(4):214-224.
Parameters Identification of Multiphase Induction Motors at Standstill
ZHENG Shida,YANG Jiaqiang
(Zhejiang University, Hangzhou 310027, China)
In order to obtain the accurate parameters of multiphase induction motor(IM) at standstill, a method was proposed based on the asymmetric T type circuit. Considering the smaller parameters of the low voltage and high power multiphase IMs than usual 3-phase IMs, voltage acquirement is via measuring phase voltage directly instead of voltage reconstruction so that the nonlinearity and compensation errors are avoided. Especially for the magnetizing inductance (approximately 8~10mH), both low-frequency injection and current dropping methods are adopted to validate the final value of magnetizing inductance. The experimental results show the validation of the proposed parameter identification method.
parameters estimation; standstill state; low-voltage &high power; multiphase induction motor
TM311
B
1000-3983(2018)06-0001-05
国家自然科学基金(面上项目)(51777191)。
2018-01-22
郑仕达(1995-),浙江大学,电机及其控制研究所,硕士研究生在读,研究方向为电机参数辨识与控制。


