绳索式3D打印机驱动装置的设计与分析

王树国，杨一通，严卫庆，张骏杰，赵 辉

（东北林业大学机电工程学院，黑龙江哈尔滨 150040）

0 引言

3D打印是一种增材制造技术，属于快速成型技术，根据零部件或者物体的三维模型数据，利用3D打印设备以材料堆积的方式制造实体的技术。随着该技术的不断创新发展，配套设备的不断升级更新，3D打印技术逐渐的被用于日常生活中。世界上第一台售价100美元的3D打印机在加拿大萨斯喀彻温省问世。2014年8月21日，苏州盈创建筑材料公司使用1台大型1的3D打印机，利用1 d时间建造了10栋200 m2的毛坯房；这台3D打印机长150 m，宽10 m，深6 m，打印出房屋的结构组件，再运到现场进行房屋的组装搭建[1-2]。

随着3D打印技术产业的不断发展，打印设备的大型化、轻型化，将是未来发展趋势之一[3]。为了实现3D打印设备的大型化、轻型化，设计了一种利用绳索作为传动机构的驱动装置。

1 绳索驱动装置描述

所设计的驱动装置主要结构由定平台、动平台和3根立柱—电机—绳索组成：绳索的一端与立柱底部的电机相连，通过立柱顶端的万向轮，从顶端绕出与动平台相连（图1、图 2）。

装置的工作流程：①步进电机旋转带动绳索；②绳索运动牵制工作平台进行运动；③通过控制电机转轴的旋转使工作平台按指定轨迹进行运动。

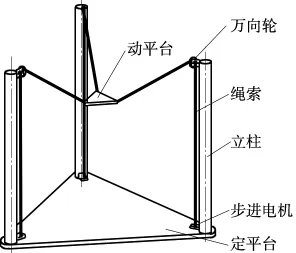
图1 驱动机构

图2 实物

2 运动学分析

2.1 运动学反解分析

驱动装置动平台的空间运动是通过电机的转动来控制的，对于动平台在空间中到达的任意位姿，3个电机均有特定的角位移与之对应。运动学反解就是当工作平台的位姿给定时，可以根据机构的运动学关系，求解各个电机旋转所收放绳索的长度、速度和加速度[4]。

建立坐标系，以定平台上表面几何中心为原点建立坐标系O—XYZ，以动平台上表面几何中心为原点建立坐标系O'—X'Y'Z'（图3）。其中，Ci（i=1,2,3）为三立柱顶端的位置，用向量表示为（1）式。

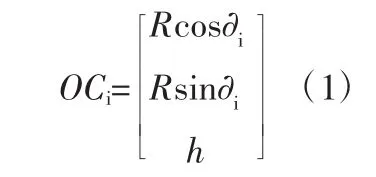
其中，∂i为 OCi与坐标系O—XYZ中X轴正方向之间的夹角i=1,2,3；R为三角形定平台的外接圆半径；h为立柱顶端到平面坐标系O—XY的垂直距离。

坐标系 O'—X'Y'Z'中，绳索与动平台的连接点Bi，用向量可以表示为（2）式。

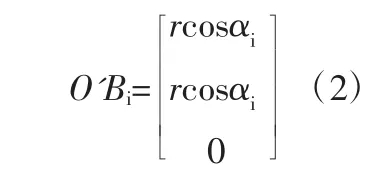
其中，αi为 OBi与坐标系O'—X'Y'Z'中 X'正方向的夹角，i=1,2,3；r为三角形动平台外接圆的半径。

设[XYZ]T为动平台中心点O'在坐标系O-XYZ下的位置向量，在坐标系O-XYZ中点Bi用向量可表示为（3）式。

图3 机构坐标分布

由此可得到向量CiBi的模li满足CiBi2=li2。将CiBi带入，得到式（5）。[X+（r-R）cos∂i]2+[Y+（r-R）sin∂i]2+（Z-h）2=li2。即

将绳索从电机连接到工作平台的总长度设计为固定值L，电机轴上缠绕的绳索长度为Δli则L=li+h+Δli，即Δli=L-li-h。将li带入，即可得到电机轴上缠绕绳索的长度即电机轴外表面上一点的线位移为：Δli=L -h -。至此，只需给出某时刻动平台几何中心的坐标，由Δli的计算公式即可求得电机轴上绳索的缠绕量即绳索收放的改变量[5，6]。在后续的Adams仿真实验中，将对推出的逆解进行仿真验证，仿真的结果将对系统的可控性、平稳性提供分析依据[7]。

2.2 运动学正解分析

运动学正解是指，已知驱动电机的电机轴外表面上某点线位移，求解平台末端的位置坐标[8]。现采用几何解析法进行运动学正解的求解[9]。可写成式（6）形式：

其中，ai=（r-R）cos∂i，bi=（r-R）sin∂i；i=（1,2,3）。整理得到式（7）。

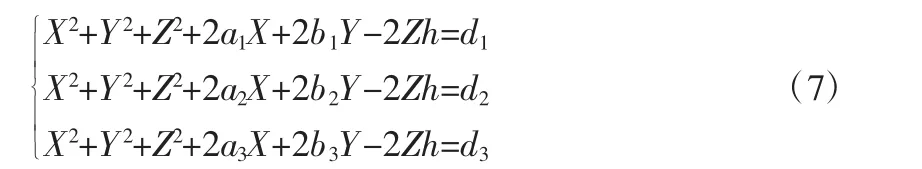
其中，di=li2-ai2-bi2-h2，将L=li+h+Δli带入得di=（L-h-Δli）2-ai2-bi2-h2，i=（1,2,3）。整理得式（8）。

因为工作平台一直位于O-XY坐标平面的上方，所以Z≥0。即

综上所述，该机构的运动学正解为式（3）和式（11）。

2.3 机械结构雅克比矩阵的推导和速度分析

该驱动机构输入运动是由3个电机的转动转化为运动平台的三维运动。构建该驱动机构的雅可比矩阵可以对其运动特性进行分析，即对输入运动和输出运动之间的关系进行分析[10]。

对式（5）进行整理得到式（12）。

其中，vx，vy，vz表示动平台几何中心在坐标系O-XYZ中X，Y，Z3个方向的速度大小，v1，v2，v3表示绳子收放速度即电机轴外径的线速度。

对式（13）进行整理得（14）：

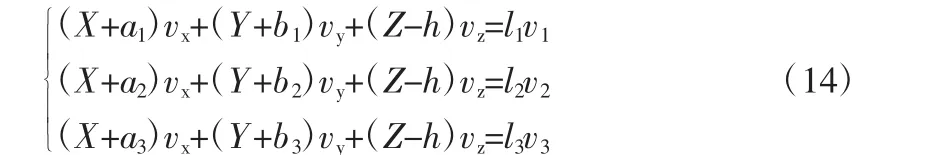
将式（13）整理成矩阵得：

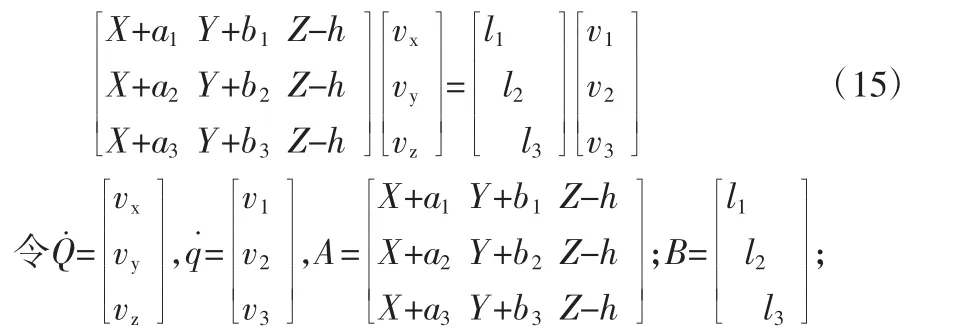
J=B-1A，则矩阵式（15）的矩阵可写成q˙=JQ˙。其中，Q˙为动平台的速度向量；q˙为绳索速度的向量。所以该驱动机构的雅可比矩阵为（16）：

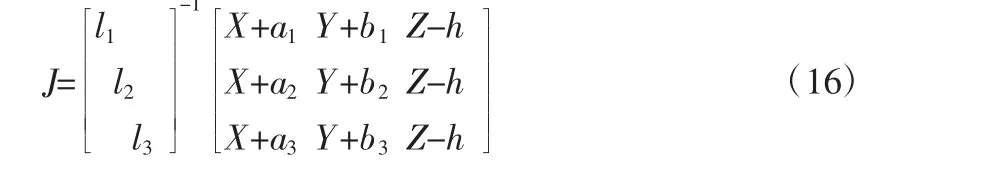
q˙=JQ˙反映了该机构的输入速度与输出速度之间的映射关系，J称为该机构的雅可比（Jacobian）矩阵，A，B分别称为正、逆雅可比矩阵。在并联机构中如果矩阵A，B其中之一或同时为0时，则并联机构出现奇异点。通过对该机构的雅可比矩阵的计算分析，得出机构的工作空间内不存在奇异点[11]。这一结论将在仿真分析中进行验证。

3 仿真实验及分析

3.1 3D模型的建立与仿真

由于该机构有些复杂，所以先利用solidworks对该驱动装置进行3D建模。建模完成后再导入到Adams中[12，13]（图4）。这里将绳索与滑块相连，用滑块的位移代替电机旋转的角位移与其电机轴半径相乘所得的线位移。

图4 机构3D模型

将建好的3D模型导入到Adams中后，需要添加运动副和驱动在构件上。运动副和驱动添加完成后，对运动学的仿真参数进行设置。仿真步数为5000步；仿真时间为5 s；将Mark点设置在动平台的中心，动平台的一些相关参数可通过测量Mark点的位置、速度得到。

根据3D打印的工作原理，选取一个平行于O-XY平面的水平面，即给定空间坐标值Z，在O-XY的平面内让动平台按照圆形轨迹进行运动。圆形的参数方程在这里设为：

其中，t表示时间。将式 （17） 带入到 Δli=L-h-。即该机构的运动学反解中，可求得滑块的运动方程，即滑块的位移函数：

将式（17）变换成Adams认可的形式代入，即可得到驱动3个滑块运动的驱动函数[14]。

3.2 仿真结果分析

在相应的驱动上添加变换后的驱动函数，添加完成后进行仿真。仿真结束后动平台中心点即Mark点在X轴、Y轴、Z轴的位移以及3个滑块位移的曲线如图5、图6所示。

从动平台位移曲线图中可以看到，在运动初始阶段3条曲线均有跃变情况。之后，X轴、Y轴、Z轴方向上的曲线，与将函数导入到MATLAB中输出的曲线图基本一致，满足理论结果，验证了上文中位置反解结果的正确性[15-17]。滑块位移曲线图较为平滑，说明运动过程较为平稳[18]。

初始阶段出现曲线跃变情况经理论分析之后，发现是因为动平台初始位置所在的水平面与动平台运动所在的平面存在高度差，动平台在从初始平面运动到运动所在平面的过程中，有一个较大的运动速度，致使动平台在进入运动平面时产生惯性，从而导致了平台的震动，才出现了图中曲线的跃变。该种情况可通过优化驱动函数、合理规划运动路径进行改善。平台的速度曲线如图7所示。

从速度曲线图可以看出，除了平台从初始位置到运动平面过渡过程中由于惯性产生的曲线跃变外，平台的运动速度曲线比较平稳[18]。图中速度曲线中的波浪线，也是由于运动刚开始阶段惯性导致震动产生的。该种情况上文已提出改善办法，这里不再陈述。

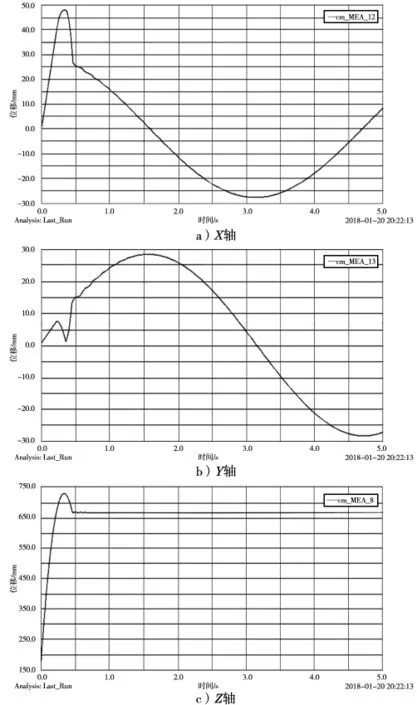
图5 Mark点3轴位移曲线

通过仿真结果发现该，驱动机构的位移、速度曲线较为平滑，无跃变，因此该机构在运动的过程中无奇异点，验证了对雅克比矩阵的分析结果；保证了机构能够平稳的进行工作[19]。

4 结论

提出一种绳索驱动装置，通过绳索作为传动装置，解决传统装置以杆件作为传动装置而产生的机构造价昂贵、设备笨重、无法大型化制造的问题。

对该机构的运动学正反解和速度雅克比矩阵进行了推导，建立了机构的运动学模型，为该机构的设计和分析提供了理论基础。应用SolidWorks软件对该机构进行3D建模并导入到Adams软件中进行运动学仿真。仿真结果验证了该推导的运动学反解的正确性。通过对仿真得到的位移、速度曲线的分析可知，当工作平台在其工作空间内进行运动时，其运动轨迹是满足要求的，工作性能稳定，在所需的工作空间内不存在奇异点。

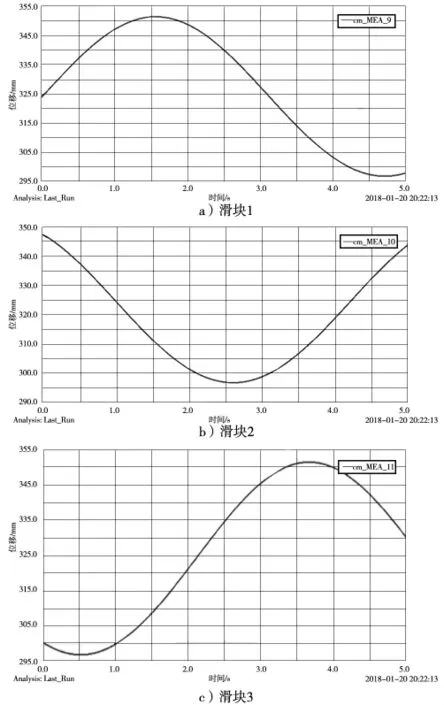
图6 3个滑块1Z轴方向位移曲线

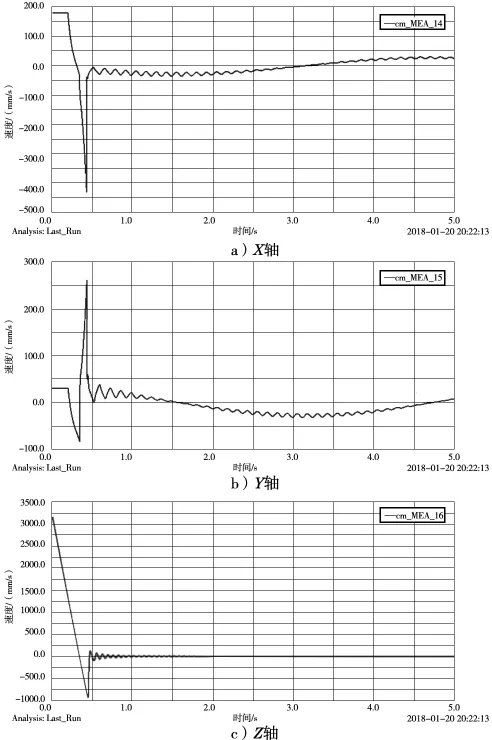
图7 Mark点3轴方向的速度