2018年西藏自治区高考理科数学评卷分析报告

◆伍劲松

2018年西藏自治区普通高等学校招生全国统一考试所用的理科数学试卷是全国卷III，试卷对高中数学的主干知识进行了考查，注重对基础知识、基本方法和技能的考查，注重对考生在数学方面的核心能力的考查。试卷的命制及内容分布符合《普通高中数学课程标准（2017年版）》的要求，试题难度适中，试题的信度和效度符合国家考试要求。

一、试卷分析

1.试卷的题型结构

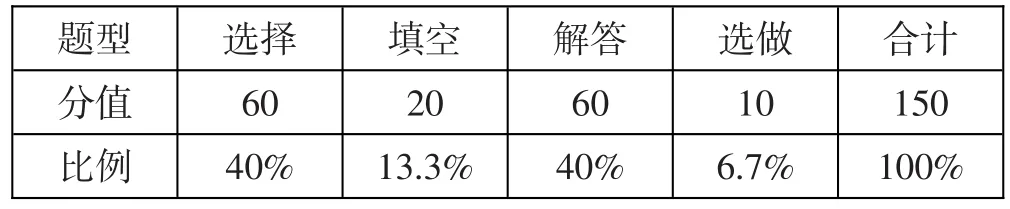
试卷的题型结构与往年保持一致。

2.试卷知识点的分数分布

选择题共计12小题：集合求交集5分；复数乘法5分；榫卯构件的三视图5分；三角函数的二倍角计算5分；二项式展开求系数5分；圆上一点到直线距离求最值5分；偶函数图象判断5分；概率5分；三角形的正余弦定理5分；多面体三棱锥体积计算5分；双曲线离心率计算5分；对数式大小比较5分；

填空题共计4小题：向量共线求参数5分；曲线切线方程5分；函数零点5分；直线与抛物线位置关系5分。

解答题共计5小题：等比数列计算通项公式和前n项和12分；统计分析中茎叶图、列联表12分；立体几何面面垂直证明和求二面角12分；直线与椭圆位置关系中的证明12分；导数在研究函数中的应用12分。

选做题为二选一：选修4-4坐标系与参数方程中参数范围及参数方程10分；选修4-5不等式选讲中画图和求最小值10分。

从知识的分类来看，函数部分考查约27分；解析几何部分考查约27分；立体几何部分考查约22分；统计、概率、二项式定理部分考查约22分；数列部分考查约12分；选修系列选做部分考查约10分；其他部分（集合、复数、算法、向量、解三角形等）考查约30分。

西藏自治区2018年的高考理科数学试卷的知识分布与往年有较大的变化，减少了程序框图、线性规划、分布列三个知识点的考查，弱化了解三角形的考查，整体试卷难度较往年有所下降。

3.试题的基本特点

第一，试题注重对学生基本知识与基本技能的考查。试卷中约有60%的试题是通过对基本知识与基本技能的考查去检验学生是否掌握了基本的数学知识和数学技能，是否达到了课程标准的基本要求。试卷考查的知识面宽，覆盖面大，减小了考查的偶然性和片面性，增强了试卷考查的公平性。

第二，试题既密切联系学生生活实际和社会实际，也注重对数学文化的学习和传承。试题重视学生的生活体验，注重紧密联系学生的生活和社会实际，注意将数学的基本知识放在真实、生动的情景中，通过学生对问题情景的分析和解决的过程来考查学生认识世界和理解世界的能力，考查学生利用所学知识分析、解决具体问题的能力，考查学生在数学学科上进一步深造的潜质。

第三，试题体现了对学生情感态度与价值观的培养，注重体现数学课程的三维目标，注重对学生的观察能力、动手能力以及对数据的归纳总结能力的考查，加强了对分析归纳等能力的考核，同时也加大了对学生的探究能力的考查力度。把探究的精神自然融合在试题当中，引导学生去发现问题、提出问题，并寻找解决问题的最佳方法和途径，充分体现了让学生自我发现、自我设计、自我分析、自我评价的探究思想。

第四，试题设置开放性问题，注重对学生创新精神和实践能力的考查。试卷中进一步加大了问题的开放程度，题目的答案具备一定的开放性，取决于学生的构思，给学生提供了思维的自由空间。

第五，试题的表述符合基本的语言习惯，没有额外增加学生阅读的困难。试题注重对基础知识、基本方法和技能考查的同时，加强了对学生数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等学科核心素养的检查。

二、答题分析

1.各个试题的得分偏低

试卷的得分情况并不理想，普遍偏低。情况如下表所示：

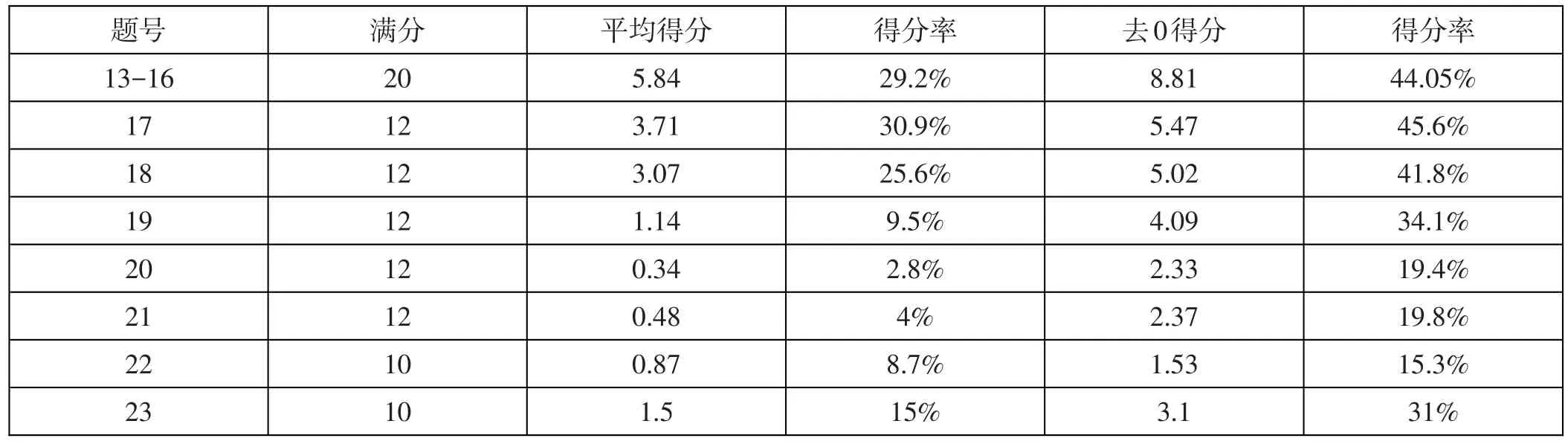
从表中可以看出，主观题的平均得分率最低的是20题，得分率是2.8%，即平面解析几何的知识得分情况最差。主观题平均得分率最高的是17题，得分率是30.9%，即数列知识得分率最高；去0得分率最高的也是数列部分知识，得分率是45.6%。由此可以看出，学生对教材中数列部分知识掌握情况较好。从选做的22题、23题来看，选做23题的学生得分率明显高于选做22题的学生得分率。

2.考查核心素养的试题具有较高的区分度

试卷中的第17题，考查学生对等比数列知识的掌握情况。题目难度中等，需要学生具备等比数列中解决问题的基本方法和技巧。第一问仅仅涉及列出方程，简单计算即可，第二问需要学生分情况进行解答。基础知识扎实、平常认真努力学习的学生对这道试题能够给出较为完整全面的解答，而那些没有掌握好基础知识的学生就无法准确地解答这道试题。因此，这道试题具有较高的区分度，能够区分认真学习数学知识和没有学习数学知识的学生。

3.立体几何的解答表述缺乏准确的计算和严谨的思维

试卷第19题是对学生立体几何知识的考查，该题第一问是考查学生证明面面垂直的能力，但需要学生对该问题仔细审查，严密推理。多数学生并未严谨推理，忽略对条件的表述，想当然地得出结论。该题的第二问是要求学生求出平面MAB与平面MCD所成角的正弦值，由于题目所给图形并未将两个平面的交线作出，需要学生具有备准确的计算能力和严谨的思维能力。从解法来看，一种是构造面面所成的角，置于适当的三角形中计算出面面角的正弦值，这种解法的难点在于如何找出二面角的平面角；另一种是建立空间直角坐标系，将面面角转化为空间中向量与平面法向量所成角的余角，难点在于求出法向量的坐标。两种解法各有优劣之处，但都需要学生具备准确的计算能力和严谨的逻辑思维能力。从学生的解答情况来看，学生的两种能力都存在较大的提升空间。

4.综合性题目的解答缺乏全面性

主观试题都具备一定的综合性，但平面解析几何和导数的考查试题更为突出。学生的答题缺乏对题目的整体把控，逻辑推理中缺乏全面性。可以看出，很多学生不能完全理解和运用解析几何中的条件，无法从题目设置的条件进行推理和计算。考查导数知识的试题中，第二问是要求学生求出参数a，条件是“若x=0是f（x）的极大值点”。这需要学生全面准确理解条件，既要分析函数极大值存在的前提条件，使得该点处函数值大于或等于邻域内的所有函数值，还要将此转化为两个关于a的不等式。多数学生只考虑了求导后导数为零的情况，而忽略了函数值在该点处的大小变化情况，体现了学生的解答缺乏全面性思考。

三、教学建议

首先，教师对学生数学学习兴趣的培养是重点。从试卷答题的情况来看，相当多的学生在试卷上仍然留下大量的空白，放弃了很多题的解答。从试题难易程度分析，很多试题仍属较为容易的档次，只要学生平常稍加认真学习，应该可以完成解答，但实际情况非常令人担忧，大量的学生放弃了对数学的学习，失去了兴趣。因此，关注并培养学生学习数学的兴趣就成为了数学教师的重点工作。

其次，高中教学过程中，数学教师应当加强对学生基本知识和基本方法的教学。学生对基本知识的掌握程度直接决定了学生在数学方面发展的潜力，没有对基本知识的学习，就不能掌握数学中的基本方法，也不可能形成数学方面的基本能力。双基教学应当落实到学生在高中学习的每一节数学课，教师应当有意识、有计划地安排这方面的教学内容。

最后，教师对学生在数学方面的核心素养关注应从高中一年级教学开始。学生核心素养的提高是一个漫长而且艰难的过程，不可能一蹴而就，需要教师不断的熏陶和影响，更需要学生不断地模仿和训练。