采用面积灰关联决策的高斯过程回归概率短期负荷预测

黄南天, 齐 斌, 刘座铭, 蔡国伟, 邢恩恺

(1. 现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学), 吉林省吉林市 132012; 2. 国网吉林省电力有限公司电力科学研究院, 吉林省长春市 130021)

0 引言

短期负荷预测是电力系统安全、稳定、经济运行的重要保障[1]。短期负荷具有不确定性、随机性等特点[2],确定性预测结果无法反映负荷变化的可靠波动范围[3]。因此,须研究概率短期负荷预测方法,以概率预测结果度量负荷变化不确定性,作为电力系统决策的依据[4]。

现有概率短期负荷预测方法根据预测结果形式分为区间预测与概率密度预测[5]。区间预测方法主要有预测误差分布特性统计法[4,6]、上下限估计法[7]、分位数回归平均法[8]、概率式预测法[9-10]等。其中,预测误差分布特性统计法对历史负荷数据需求大,专家划分负荷统计区段主观性强。概率密度预测研究多集中于基于分位数回归的概率密度预测法[11-12],预测模型耗时随模型结构复杂度增加明显上升[12]。

概率式预测法中,高斯过程回归(Gaussian process regression,GPR)方法参数少,自适应确定超参数,非参数推断灵活[13]。相较预测误差分布特性统计法,预测结果有概率意义[14],无须统计历史预测误差;相较基于分位数回归的概率密度预测法,无须对每一分位点建模,模型结构更简单。协方差函数是构建GPR预测模型的关键[15],为选择合适的协方差函数,构建最优GPR模型,须采用确定性与概率性评价指标评价模型概率预测效果[10,16]。但不同指标各有侧重,概率负荷预测多指标评价时,易存在指标间结论相互冲突的问题:最优确定性、概率性指标不统一于同一模型[10,12],或覆盖率与区间宽度等概率性指标间相互矛盾[5,17]。多指标评价体系中,各指标结论不一,使决策困难增加[18]。因此须综合评价概率负荷预测模型,避免评价的主观性与片面性。

目前,针对综合评价概率负荷预测模型问题,鲜有研究,评价上存在区间评价缺失[4,6],指标间结论冲突等问题[10]。覆盖—宽度准则(coverage width-based criterion)、温克勒分数(Winkler score)等指标将覆盖率与区间宽度相融合[16,19],应用于神经网络训练或模型评估等研究[8,20],但未考虑确定性指标对整体评价的影响。为此,考虑到综合评价方法能够综合多指标做出整体性评价的优势[21],及在负荷预测领域的有效应用[22-23],引入适当方法综合评价概率预测模型。

常用综合评价方法有层次分析法、模糊综合评价、灰色关联度结合理想解法等[24-26]。层次分析法主观性强,专家偏好对评价结果影响很大[21,24];模糊综合评价在隶属度和权重确定、算法选取等方面带有主观性[21,27];灰色关联度结合理想解法可排除主观干扰[21,26],但关联系数仅考虑不同方案指标间点对点距离,分析效果不够理想[28],忽略了不同指标间的相互影响[29]。采用面积灰关联贴近度决策,以两方案指标序列相邻指标间面积作为关联系数,可全面反映指标间相互影响,及不同方案指标序列的距离接近程度与几何形状相似程度[28-29]，更适用于评价指标间存在冲突的概率预测模型。

为克服概率短期负荷预测多指标评价决策难题,提出采用面积灰关联决策综合评价基于不同协方差函数的GPR预测模型概率负荷预测能力,以确定最优预测模型并开展概率负荷预测的新方法。通过对比实验,验证新方法有效性与先进性。

1 基于GPR概率短期负荷预测模型

1.1 高斯过程回归预测模型

高斯过程是随机变量的集合,其中任意有限个随机变量服从联合高斯分布。给定包含n个样本的训练集D={(xi,yi)};i=1,2,…,n;xi∈Rd,yi∈R。定义训练输入矩阵X=[x1,x2,…,xi,…,xn]T,xi为某一样本的d维输入向量;训练输出向量y=[y1,y2,…,yi,…,yn]T,yi为某一样本的标量输出值。xi对应的函数空间f(x1),f(x2),…,f(xn)构成的随机变量集合f(X)服从联合高斯分布,统计特性由均值函数m(X)与协方差函数K(X,X′)确定,X′为或与X相同的样本集输入矩阵,高斯过程函数GP(·)为:

f(X)～GP(m(X),K(X,X′))

(1)

对于回归问题,统计模型为:

y=f(X)+ε

(2)

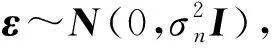
相应得到输出向量y的先验分布为:

(3)

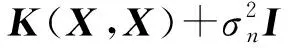
(4)

相应地,测试集输出向量f*的后验分布为:

(5)

(6)

cov(f*)=K(X*,X*)-K(X*,X)(K(X,X)+

(7)

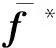
置信水平为1-a的置信区间为:

[L1-a(f*),U1-a(f*)]=

(8)

式中:U1-a(f*)和L1-a(f*)分别为置信区间的上下限;z(1-a)/2为相应置信水平下的分位数。

1.2 协方差函数选择问题

监督学习的基本假设是输入值相近的点很可能有相似的目标值。GPR中,协方差函数便定义了这种临近性与相似性,模型性质由均值函数与协方差函数决定,通常为简易符号,使函数均值为0。因此,选择合适协方差函数是优化GPR模型的关键。这里,采用10种协方差函数开展对比实验[15],10种协方差函数名称、公式见附录A表A1。

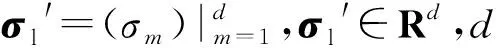
1.3 概率短期负荷预测多指标评价问题

为选择协方差函数,构建最优GPR模型,需要评价不同模型概率预测效果。不仅需要确定性评价指标,包括平均绝对百分误差(MAPE)、最大相对百分误差(MRPE)、均方根误差(RMSE)等;还需要概率性评价指标,包括预测区间覆盖率(PICP)、预测区间归一化平均宽度(PINAW)等[7]。以上指标各有侧重,MAPE将误差百分化,便于比较确定性预测结果精度[31];MRPE能够反映预测时段内最大预测误差;RMSE对离群值更为敏感,适用于辨识模型间差异[32];PICP表征预测区间的可靠性,即预测区间对真实值的覆盖率,值越大区间越可靠;PINAW表征预测区间精锐程度(sharpness),值越小,区间上下限与真实值越贴近[16],区间过宽便失去了决策参考价值[12]。当从多方面评判概率模型优劣时,易存在指标间结论相互冲突的问题[10,12]。因此,须综合评估模型概率预测能力,避免评价的主观性与片面性。

2 面积灰关联决策

为解决概率预测模型评价指标结论相互冲突的问题,确定最优GPR模型及相应协方差函数,引入面积灰关联决策方法开展综合评价[28-29]。

2.1 构造综合评价矩阵并确定指标权重

以MAPE,MRPE,RMSE,PICP,PINAW等5个指标构成评价指标集合。各指标公式及公式参数见附录A表A2。

采用评价指标集合评估基于不同协方差函数的GPR模型,得到各GPR模型的指标序列,作为备选方案,以构造综合评价矩阵。

设有m个备选方案,n个评价指标,指标值为aij(1≤i≤m,1≤j≤n),相应的综合评价矩阵A=(aij)m×n。为消除指标间量纲和数量级影响,对综合评价矩阵A标准化处理为X=(xij)m×n,当A的第j(1≤j≤n)列m个指标为效益型或成本型指标时，分别利用式(9)或式(10)对该列指标标准化。

(9)

(10)

在综合评价矩阵基础上,计算指标权重,指标权重体现着指标包含信息量,越大指标越重要,直观反映了指标间差异程度[33-34]。为避免主观因素对指标权重的影响,采用熵权法客观赋权[33],由n个指标权重构成权重向量B,确定各评价指标相对评价目标的重要程度,其中B=(wj)1×n,1≤j≤n。采用熵权法确定指标权重的计算过程见附录B。赋权方法的选择对于指标权重或有较大影响,未来为克服这一影响,考虑根据综合评价结果择优选择赋权方法或组合赋权。

2.2 计算灰关联贴近度

为充分利用决策信息,依据理想解法思想,定义灰关联贴近度模型。在灰关联贴近度模型中,为反映指标间相互影响,采用备选方案与最优、最劣方案相邻指标间所围成的面积,计算关联系数。

首先,确定最优、最劣方案R+和R-分别为:

(11)

(12)

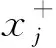
(13)

(14)

在此基础上,计算相应最优、劣面积关联系数为:

(15)

(16)

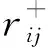
最后,集合将所有备选方案在各指标下的关联系数,确定优、劣关联系数矩阵R+和R-为:

(17)

(18)

之后,定义并计算备选方案与最优、最劣方案的灰色关联度,作为方案优选的测度。

(19)

(20)

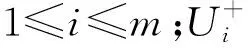
最后,为能够测度备选方案与最优、最劣方案动态变化趋势一致性,定义灰关联贴近度Ci,根据Ci对备选方案排序,值越大方案越优,即

(21)

3 算例分析

3.1 算例描述

选择中国某城市2011—2012年实际负荷数据用于算例。新方法首先从2011年365 d样本中随机选取110 d样本作为验证集,剩余255 d样本作为训练集。然后,采用训练集训练基于不同协方差函数的10个GPR预测模型,并在验证集上验证各个GPR模型预测效果,得到各模型确定性预测结论与置信度为95%的预测区间。继而,采用MAPE,MRPE,RMSE等3种确定性指标与PINAW和PICP等2种概率性指标评价预测结果,以评价指标构造综合评价矩阵,作为面积灰关联决策的输入;之后采用面积灰关联决策对10个GPR模型开展综合评价,给出各GPR模型距离、面积灰关联决策的贴近度与排序,确定最优GPR模型。最后,从2012年4个季度中分别选取一个月的负荷数据作测试集(文中选择3,5,9,11月),在测试集上测试最优GPR模型预测结果并评价。

根据对负荷自相关性和周期性的分析[36-37],确定预测模型的10个输入特征,包括7个负荷特征和3个周期特征。负荷特征分别为待预测时刻t前h小时t-h时刻的负荷值Lt-h;h分别为24,48,72,96,120,144,168 h。周期特征分别为星期特征、月份特征、工作日特征。其中,星期特征根据待预测时刻负荷所属星期几,给定1到7的整数;月份特征根据待预测时刻负荷所属月份,给定1到12的整数;工作日特征根据待预测时刻负荷是属于工作日(周一至周五)还是周末(周六至周日),给定1或0。

为验证由上述方法得到的最优GPR模型先进性,在同一训练集上训练支持向量机(SVM)和随机森林(RF)模型,在测试集上对比最优GPR模型与SVM和RF模型的确定性预测结果;与基于最优GPR,SVM,RF模型的预测误差分布特性统计法模型的概率预测结果。对比实验中,使用网格法确定SVM参数,惩罚因子C为16,核参数σ2为1.624 5。RF主要参数为树的数量ntree和分裂特征数mtry[22]。ntree不宜偏小,根据尽量使每一样本至少进行几次预测的原则,调试为500则足以获得较好的预测效果[36];回归问题中,mtry可依经验公式mtry=n′/3定为10/3,n′为输入特征个数[38]。

采用预测误差分布特性统计法实现概率短期负荷预测时,需引入某一预测模型得到的确定性预测结果统计预测误差分布特性。本文中,以GPR模型得到的确定性预测结果作为统计样本时,称基于GPR的预测误差分布特性统计法(EGPR);用GPR模型得到确定性与概率短期负荷预测结果时,称GPR方法。

预测误差分布特性统计法中,采用非参数核密度估计法,统计不同预测模型在各测试集前两个月的确定性负荷预测误差:依照各测试样本所在季节典型日负荷曲线划分统计时段;依据使每个负荷区段的预测误差样本数量满足统计要求的原则,结合算例实际,将负荷区段样本数参考区间定为[128,192][4,6]。

3.2 基于不同协方差函数的GPR模型预测结果分析

采用MAPE,MRPE,RMSE,PICP,PINAW等5个指标评价验证集4个季度下各GPR模型预测结果,统计得到各季度下5个指标,共计20个最优指标值及其对应的GPR模型,相应得到20个最劣指标值及其对应的GPR模型。图1给出各GPR模型编号与名称,标明了各GPR模型所占最优、最劣指标值比例。10种GPR模型名称与对应的协方差函数名称一致，见附录A表A1。

图1 各GPR模型最优最劣指标占比Fig.1 Proportion of optimal and worst indicators for different GPR models

由图1可知,最优、最劣指标分布在各GPR模型比例并不均匀且有集中趋势,编号8的ARD-M3-GPR模型所占最优指标比例最高;编号2和10的GPR模型共占有85%的最劣指标;编号3和5的GPR模型不占有最优、最劣指标,表明基于不同协方差函数构建GPR模型,对其预测效果存在明显影响。

通过分析4个季度下最优、最劣指标值及其对应的GPR模型,发现各评价指标结论存在冲突,即各评价指标最优值不统一于同一模型,甚至最优与最劣指标出现于同一模型。以一季度为例,各指标最优值对应的GPR模型编号分别为8,2,8,1,10;但由图1可知,编号2,6,7,10的GPR模型既存在最优指标,又存在最劣指标。多指标评价结论存在冲突说明开展综合评价、确定最优预测模型的必要性。不同季度下各GPR模型预测结果评价详情,请参阅附录C图C1。

3.3 面积灰关联决策结果分析

为解决评价指标冲突问题,综合评价验证集的预测结果,构造综合评价矩阵,如表1所示。

表1 基于不同协方差函数的GPR模型预测结果分析Table 1 Prediction result analysis of GPR model based on different covariance functions

表中GPR模型名称编号与图1一致。可以看出，各指标最优值分散在4个GPR模型上,即表中红色数值，不统一于同一GPR模型,最优模型难以确定,进一步说明开展综合评价的必要性。

通过熵权法获得的MAPE,MRPE,RMSE,PICP,PINAW等指标权重依次为0.180 1,0.170 4,0.169 1,0.234 7,0.245 7。随后,表2给出各GPR模型的面积、距离贴近度及排序、相邻GPR模型面积贴近度差值与距离贴近度差值的比值,即贴近度差值比,表中GPR模型名称编号与图1一致。结合表1知,编号8的GPR模型在5个指标中的两个均为最优,还有两个排序第2并与第1差别很小,是最为倾向选择的对象;同样编号6和9的GPR模型各指标排序整体靠前,是较为倾向选择的对象,这与表3中面积灰关联决策排序结果一致。表中，ESVM,ERF,EARD-M3-GPR,分别表示基于SVM,RF,ARD-M3-GPR模型的预测误差分布特性统计法。说明面积灰关联决策结论与原始决策信息相一致,反映该方法的可靠性。

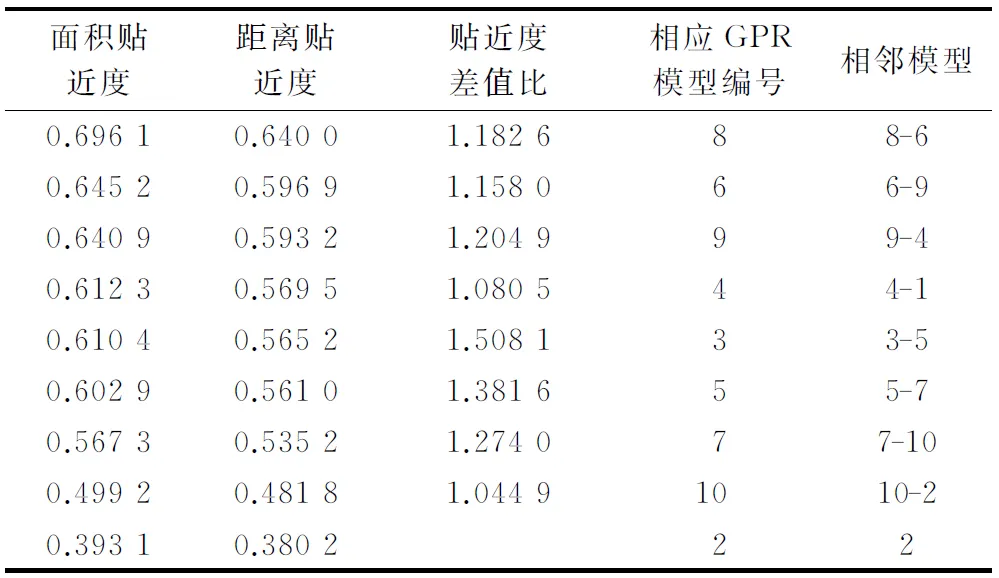
表2 GPR模型排序Table 2 GPR model sort

表3 各模型预测区间分析Table 3 Prediction interval analysis for each predictor

算例表明,采用ARD系列协方差函数,有效提升了GPR模型预测能力;以最优模型开展预测,相较对比方法,最优模型在保证确定性预测精度的同时,预测区间更精确可靠,准确刻画了负荷的波动性,区间上限更低,有助于为决策提供更多有效信息。

未来工作集中于针对概率短期负荷预测特点的特征选择与考虑高比例可再生能源接入后对负荷波动性影响研究。

由于灰关联贴近度方法从相对的角度区分方案间差异,考虑了多方面因素的影响,因此,只要贴近度大小不同就可以表明方案间有差别,区分度较高[29]。结合表2可知,面积、距离灰关联决策对各GPR模型排序一致;但由贴近度差值比可知,排序靠前(前5个)的相邻GPR模型间,面积贴近度差值均大于相应距离贴近度差值,表明面积灰关联贴近度决策对不同GPR模型区分度更大,更明确地分辨方案间差异,凸显了优势GPR模型,结论更可靠。

相较EX和RQ协方差函数,SE,M3与M5协方差函数排序更靠前,表明协方差函数形式对GPR模型预测效果影响明显;排序前6的协方差函数中,相较协方差函数σl为标量的GPR模型,采用ARD系列协方差函数的GPR模型排序更靠前,表明在确定合适协方差函数形式基础上,采用ARD系列协方差函数,有效提升了GPR模型预测能力。

最终,依照上述分析,采纳面积灰关联贴近度决策结论,并确定ARD-M3-GPR模型为最优模型。

3.4 ARD-M3-GPR模型确定性与概率预测结果分析

为进一步验证最优模型预测效果,在测试集上比较ARD-M3-GPR模型与基于SVM和RF的预测模型确定性预测结果,分析表明ARD-M3-GPR模型确定性预测精度有保证。预测结果与分析请参见附录C表C1。

并比较ARD-M3-GPR模型与ESVM，ERF，EARD-M3-GPR模型置信水平为95%的预测区间,如表3所示。由表3可知,相较于各预测误差分布特性统计法,ARD-M3-GPR模型覆盖率最高、宽度最窄,即保证区间高覆盖率的同时,显著降低了区间宽度。表明ARD-M3-GPR模型获得的预测区间更加精确可靠。

图2为各月测试集下随机1 d的ARD-M3-GPR模型与各预测误差分布特性统计法模型置信水平为95%的预测区间。同时在附录C图C2给出各月测试集下各模型随机一周的置信水平为95%的预测区间,以便于比较更长周期上各模型差异。

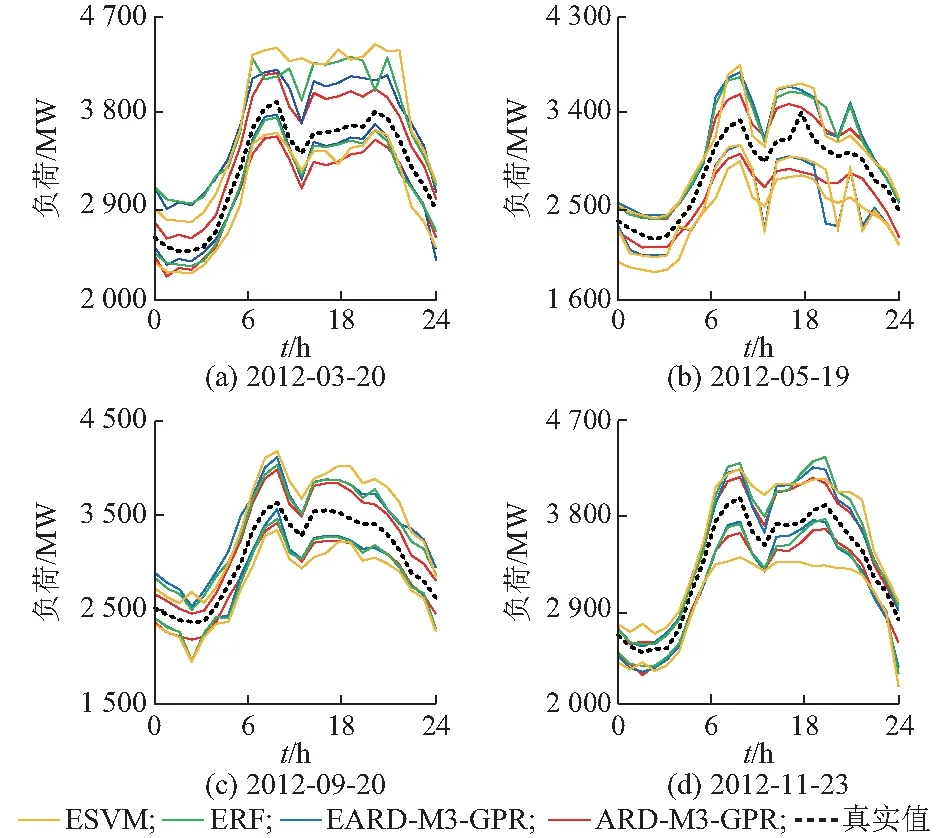
图2 各概率短期负荷预测模型的区间预测结果Fig.2 Interval forecasting results of each probabilistic short-term load forecasting model

从图2可以看出,ARD-M3-GPR模型获得的预测区间更窄,区间上限明显更低,有助于为决策提供更多有效信息;区间边界紧随真实值的改变而变化,变化最平稳,而其他区间边界存在偏离真实值变化趋势的抬升或跌落,说明ARD-M3-GPR模型得到的预测区间准确刻画了负荷的波动性。

4 结语

本文面积灰关联决策综合评价基于不同协方差函数的GPR模型概率负荷预测效果,确定最优模型。这一方法以面积关联系数替代传统的距离关联系数,更明确地分辨方案间差异,结论更可靠,有效解决了概率负荷预测中,多指标间存在冲突的问题。

本文受到吉林省教育厅“十三五”科学技术研究项目资助,特此感谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。