输电线路零序阻抗参数典型抗干扰测量方法的分析与仿真

胡志坚, 傅晨宇, 倪识远, 罗福玲

(武汉大学电气工程学院, 湖北省武汉市 430072)

0 引言

输电线路参数是电力系统重要的参数[1-2],精确测量输电线路参数对提高电力系统的安全运行水平具有重要的意义[3-5]。近年来受线路走廊的限制,同杆多回路架设及共走廊的线路越来越多,因此实际环境中待测输电线路周边通常会存在正常带电运行的输电线路[6-8]。这些带电运行的线路通过线路间的电磁耦合在待测输电线路上产生很大的感应电压和感应电流[9],该感应电压和感应电流不仅严重影响了输电线路参数测量的精度[10],而且威胁测试人员的人身安全。通常情况下,由于各种原因,不便或难以测量干扰线路自身的零序电流及被测量线路与干扰线路之间的零序互参数,因此需要采用抗干扰测量方法对输电线路的参数进行测量。

目前测量输电线路零序参数的抗干扰方法大体上可以分为工频法[11-15]和异频法[16-17]两种。工频法和异频法的区别在于施加测试电源的频率不同。工频法主要包括:①增量法,通过采用测量信号增量的方式来抑制干扰[18-20];②倒相法,通过反接电源极性方式抑制干扰[21-22];③大电流法,通过提高测试电源容量,提高信噪比降低干扰的影响[23];④干扰法,直接以工频干扰信号为测量源[24-25]。工频法实现的前提是干扰短时间不变[26];异频法向被测线路施加异频电源,由于测试信号的频率与工频干扰信号频率不同,很容易实现工频干扰的滤除[11,17]。阻抗参数受集肤效应影响较大,一般情况下,异频法施加测试信号的频率与工频相差3～5 Hz。电容参数的集肤效应影响较小,文献[27]提出了一种基于三次谐波分量的输电线路电容参数抗干扰测量方法。

在现有的抗干扰方法研究中,通常只讨论一种方法消除干扰,各抗干扰方法之间未进行比较;此外现有文献对各抗干扰方法的研究偏理想化,考虑的因素较少。例如,异频法[17]未考虑运行线路上变压器的零序阻抗大小对测量结果的影响;增量法[25]未考虑增量的大小对测量结果的影响。另外现有文献对以上各种抗干扰方法的优缺点也只有定性描述,未进行仿真验证与定量分析。

本文通过研究5种典型输电线路零序阻抗参数抗干扰方法的测量方法和测量过程,从原理上分析了这些典型的抗干扰测量方法的测量误差来源,并利用PSCAD软件建立测量模型进行仿真分析。另外,还分析了测量仪器分辨率对各抗干扰测量方法的影响。随后,本文通过设定两种典型的干扰测量环境,通过仿真得到两种情形下5种典型抗干扰方法的误差大小排序。本文研究结果可为实际线路零序阻抗参数测量中抗干扰测量方法的选取提供依据和参考。

1 零序阻抗参数测量原理

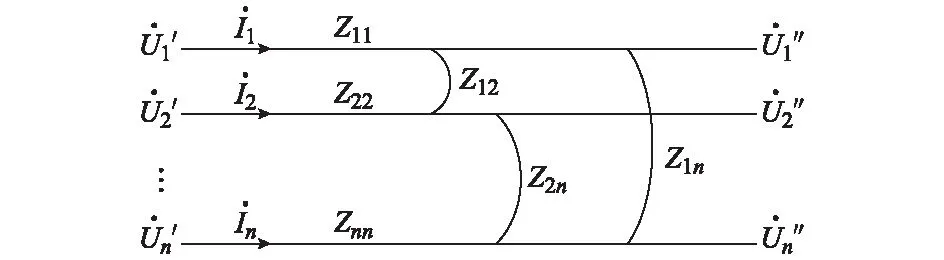
图1 输电线路零序参数模型Fig.1 Model for zero sequence parameters of transmission lines

稳态时,图1所示的互感线路的伏安特性可用如下代数方程组描述[10]。

(1)

ZI=U

(2)

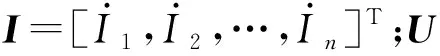
因此需要对n条互感线路进行p(p≥n(n+1)/2)次独立方式下的测量,获得p个独立方程,最后利用最小二乘法求解,便可求出这些未知的阻抗参数[9]。

2 抗干扰方法原理简介

由于带电运行线路(本文称为干扰线路)与被测线路存在电磁耦合,因此会在被测线路上感应出零序电压与零序电流,可用如附录A图A1所示的干扰线路模型表示。

附录A图A1中,干扰线路为正常带电运行的线路3,可视为多回带电运行线路的等值线路,线路1和线路2为被测线路。

考虑有干扰的情况下,根据图1和式(1)可列出附录A图A1所示的有互感耦合线路的伏安特性为:

(3)

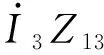
由上述测量误差来源的分析可知,如果不在测量过程中消除或者减小干扰,将会极大地影响线路参数测量结果的精度,因此现有研究提出了多种输电线路零序参数抗干扰测量方法。下面简要介绍5种典型的输电线路零序阻抗参数抗干扰测量方法的原理。

2.1 增量法

由于运行线路的负荷处于动态变化中,因此线路间的互感耦合导致的感应电压也会随之变化,但在较短时间内,该感应电压可以被认为是不变的,即干扰短时不变。

增量法是一种采取测量线路电压增量和电流增量从而得到被测线路零序阻抗参数的方法[18],该方法简述如下。

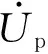
(4)

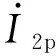
(5)

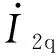
式(4)与式(5)相减得到：

(6)

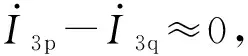
(7)

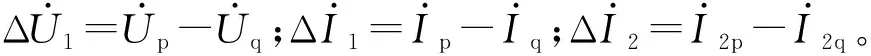
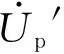
重复上述测量过程,得到另一个测量方程为:

(8)

联立求解式(7)和式(8),便可求出线路的零序阻抗参数Z11和Z12。

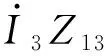
2.2 异频法

异频法[17]采用异频电源代替工频电源作为测试电源,以避开测量过程中的工频干扰,通过提取测量信号中的异频零序电压与异频零序电流,然后进行计算得到异频零序阻抗,再进行频率折算后得到线路的工频零序阻抗。

异频法的测试信号的频率是f1=f0-Δf,f2=f0+Δf。其中,f0=50 Hz;Δf通常为3 Hz或5 Hz。由式(1)可以得到异频测量时稳态情况下互感线路的伏安特性为:

(9)

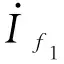
两种频率下的异频电阻Rij(·)和电感Xij(·)分别为:

(10)

最后根据测量频率对电阻参数和电抗参数进行频率折算,可得出各线路在工频下的零序自阻抗和线路间的零序互阻抗[13],折算公式为:

(11)

传统异频法[16]只消除了工频干扰但未考虑被测线路上的异频干扰,因此在测量原理存在缺陷。文献[17]提出了将附近运行线路纳入整体测量的新型异频测量方法。由于该方法在测量模型上没有考虑干扰线路上变压器的零序阻抗对异频电流的影响,测量模型不够全面,因此仍然存在测量误差。

2.3 倒相法

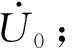
得到上述测量数据后,代入式(12)至式(14),得到被测线路零序自阻抗Z0和自阻抗角θ为:

(12)

(13)

Z0=|Z0|∠θ

(14)

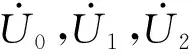
倒相法的测量误差主要来源于在倒相法操作过程中,即便可以做到使倒相前后电流的幅值相等,但难以保证倒相前后电流的相角也相等;另外干扰也不是不变的。

2.4 干扰法

干扰法是利用被测线路上的工频干扰对线路零序参数进行测量的方法[24]。其测量原理简述如下。

设有n条互感线路,编号分别为1,2,…,n。当被测线路退出运行时,受周围正常运行线路电磁感应影响,被测线路上会耦合出零序干扰电压。干扰法的核心是利用该干扰信号当作测试电源。

依次将n条互感线路中的某一线路停电,测量停电线路上的零序感应电压,同时测量其他运行线路上的零序电压和零序电流,得到n个代数方程组为:

ZIint=Uint

(15)

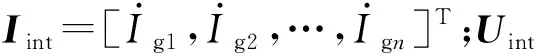
测量多种独立方式下的数据后,代入式(15),利用最小二乘方法解式(15),就可得到线路的零序阻抗参数矩阵Z。

2.5 大电流法

提高信噪比是一种常用的抗干扰测量方法[23],其核心在于通过增加测量电源的大小,从而减小干扰分量所占比例,达到减小测量误差的效果,信噪比RSN的定义为:

(16)

式中:Vs和Vg分别为测量电源电压和干扰电压的有效值,线路零序阻抗计算公式同式(1),其计算过程不再赘述。

3 仿真分析

3.1 仿真模型

利用PSCAD软件建立仿真模型如附录A图A3所示。线路A和线路B零序参数相同,为同塔双回线路,线路长度为100 km,另外在线路A,B附近有一条电压等级为110 kV的线路C与待测线路平行架设,用于模拟周边运行输电线路对测试线路产生的干扰,干扰线路C上变压器的零序阻抗为30 Ω,待测线路参数如附录A表A1所示,干扰线路C与被测线路A,B的零序互阻抗参数如附录A表A2所示。经测量,被测线路末端三相短接接地时,线路上的感应电压为100 V。

测量相对误差re定义为:

(17)

式中:Xm为测量值模值;Xt为理论值模值。

3.2 增量法仿真结果

设定干扰线路与被测线路平行架设部分的长度为30 km,通过改变前后两次施加的电压幅值差(增量大小),得到被测线路的零序阻抗测量结果及误差如表1所示。表中,R0为线路零序自电阻测量值;Rm为被测线路之间的零序互电阻测量值;L0为线路零序自电感测量值;Lm为被测线路之间的零序互电感测量值。

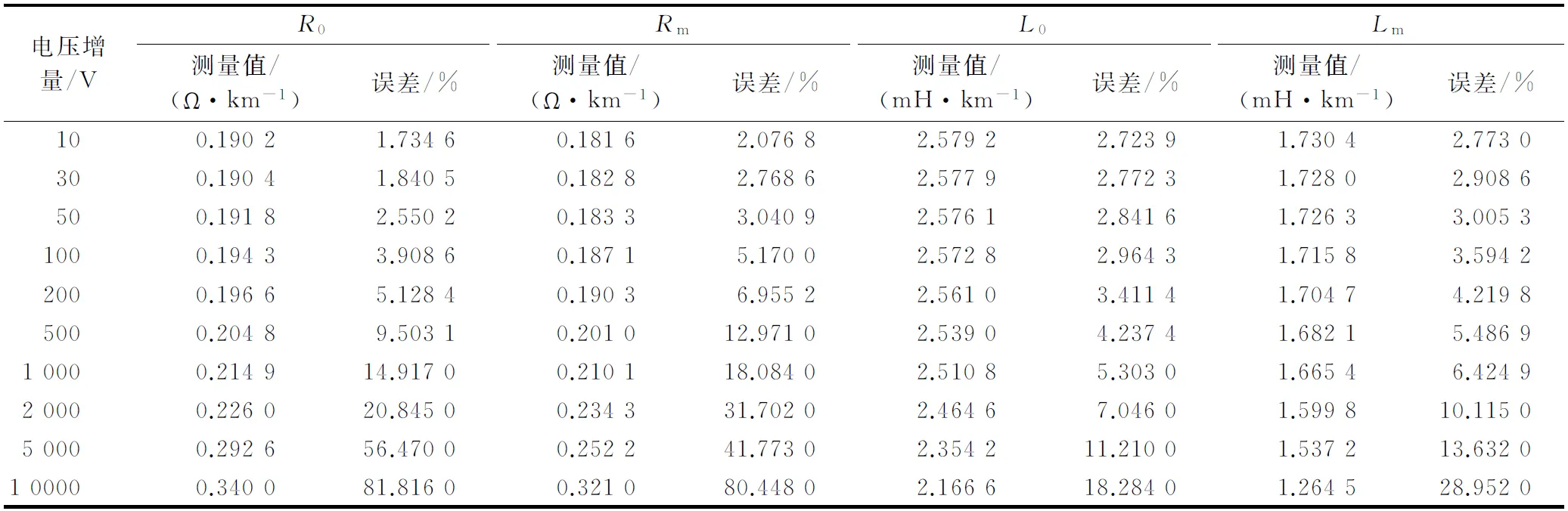
表1 不同电压幅值差下零序阻抗测量结果及相对误差Table 1 Measurement results and relative errors of zero sequence impedance under different voltage amplitudes

设定干扰线路长度与被测线路长度比例不变,改变被测线路长度,得到使被测线路自电阻测量误差小于4%时的最小增量值如图2所示。

图2 合适增量的选取Fig.2 Selection of appropriate increment

在前后两次测量电压增量为200 V的情况下,改变与被测线路耦合的干扰线路长度以及干扰线路的电压等级,得到被测线路的零序自电阻测量结果及误差如附录A图A4所示。

由表1、图2和附录A图A4可以得出如下结论。

1)随着被测线路前后两次施加的电压增量的增大,零序阻抗测量结果的相对误差逐渐增加。因此对于增量法中增量的选取,应在满足设备分辨率的基础上尽可能小。而对于合适增量的选取,可以看到,在干扰条件相同的情况下,当被测线路长度越长时,可以选择的增量越大。这是由于当被测线路长度越长时,在相同的加压条件下,两次加压时被测线路上的干扰感应电压差值会越小,由此带来的测量结果误差就越小,因此可选取的增量越大。

2)在其他条件保持不变的情况下,随着干扰线路长度的增加,被测线路零序阻抗的误差逐渐增加。由此可以看出,当干扰线路与被测线路之间的互感较大或者两次施加的测量电压值的增量过大时,会导致两次加压时被测线路上的干扰感应电压值不一致,在计算增量时不能完全消除干扰,从而使测量结果的相对误差增大。同样地,当被测线路周围的干扰变化时,也会对测量精度产生影响。

3)当干扰线路与被测线路之间的互感保持不变时,干扰线路自身的电流大小对测量结果影响非常小,因为由干扰线路自身的电流产生的干扰量在计算增量时基本被消除了,所以对测量精度影响很小。因此,影响增量法测量结果精度的主要因素是干扰线路与被测线路之间的互感大小、两次施加的测量电压值的增量值以及测线路周围的干扰的稳定程度。

3.3 异频法仿真结果

传统异频法[16]由于只消除了工频干扰但未考虑被测线路上的异频干扰,因此测量原理是存在缺陷的。文献[17]提出了将附近运行线路纳入整体测量的新型异频测量方法,由于该方法在测量模型上没有考虑干扰线路上变压器的零序阻抗,测量模型不够全面,因此仍然存在测量误差。

在保持干扰线路长度不变,并且与被测线路平行架设长度为30 km的情况下,改变运行线路上变压器的零序阻抗大小,采用新型异频测量方法得到被测线路的零序阻抗测量结果及误差见附录A表A3。

由附录A表A3中的仿真结果可以看到,运行线路上的变压器零序阻抗对异频法的测量结果是有影响的,并且零序阻抗越小,由此产生的误差越大,当变压器零序阻抗足够大时,异频法的测量结果很准确。但实际上,星形/三角形接线的变压器零序阻抗通常在30～50 Ω左右[28],因此,异频法的测量误差仍然较大。

当线路上变压器零序阻抗分别为10,30,50,100 Ω时,在保持干扰线路与被测线路平行架设长度为30 km不变的情况下,改变干扰线路自身的长度,得到被测线路的零序自电阻测量误差变化如图3所示。

由图3可以看到, 在干扰线路与被测线路平行架设的长度以及运行线路上变压器零序阻抗保持不变的情况下,随着干扰线路长度的增大,测量误差减小。这是由于干扰线路长度较大时,干扰线路自身的零序阻抗也较大,因此变压器零序阻抗对运行线路的电流影响较小,从而在被测线路上造成的干扰较小。

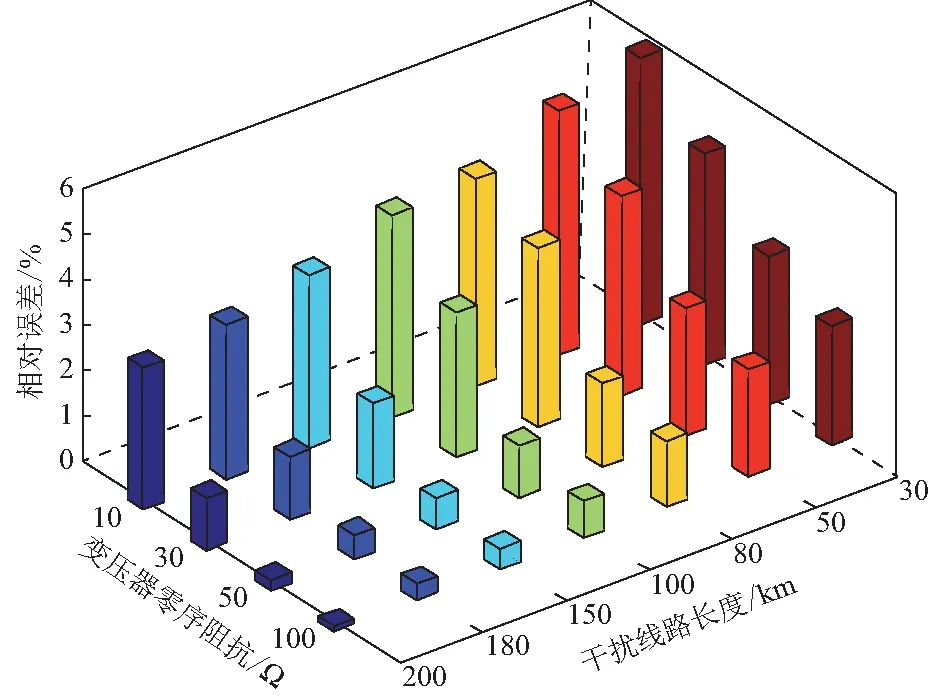
图3 零序自电阻测量相对误差Fig.3 Relative errors of zero sequence self-resistance measurement

3.4 倒相法仿真结果

由2.3节所述的倒相法测量过程可以看到,倒相法消除干扰的原理是建立在被测线路上的干扰保持不变的前提下,若测试电源反相前后干扰电压发生改变,倒相法的测量结果就会产生误差。

通过改变干扰线路长度得到被测线路的零序阻抗测量结果及相对误差如附录A表A4所示。

由附录A表A4可以看出,随着干扰线路长度的增加,测量线路零序阻抗的相对误差逐渐变大。这是由于测试线路上的干扰电压很大时,使式(13)中的两个阻抗相角在相加后无法抵消其中的干扰,从而使计算出的零序阻抗角产生误差。

另外如果被测线路附近的干扰发生改变,对测量结果的影响也很大。在实际现场中,上述的反相操作的时间可能将长达数十秒至数分钟,干扰电压U0的相位和幅值在这段时间很可能发生变化,从而产生很大的误差。

在不改变干扰线路长度的情况下,改变干扰线路的电压等级,即改变干扰线路自身的零序电流大小,得到被测线路的零序自电阻测量误差见附录A图A5。

由附录A图A5可以看出,在其他条件保持不变的情况下,随着干扰线路自身零序电流的增大,测量结果误差变化很小。由此可以得到,影响倒相法测量精度的主要因素是干扰线路与被测线路之间的互感大小以及测线路周围的干扰的稳定程度。

3.5 干扰法仿真结果

通过设定两回线路不同的同塔长度以及改变干扰线路的输入电压(即改变干扰大小),利用干扰法测量得到被测线路的零序阻抗测量结果及误差如附录A表A5所示。

由附录A表A5可以看出,随着干扰线路的长度增加,使用干扰法测得的线路参数的误差逐渐增大。这是由于当被测线路与干扰线路的互感较大时,在对被测线路测量开路电压和短接电流后,干扰线路上的电流值变化很大,在前后采集电压和电流的过程中,干扰发生了改变,使得测量误差增大。

设定干扰线路长度为30 km不变,通过改变干扰线路的电压等级,得到测量结果误差如附录A图A6所示。

从附录A图A6可以看出,当改变干扰线路的电压等级后,测量结果几乎没有变化,说明在周围干扰稳定的情况下,干扰本身的大小对测量误差没有影响。但是干扰法在测量过程中不需要添加外部电源,完全通过采集被测线路上的干扰信号来计算得到线路的零序参数,因此在运行线路负荷有较大波动的情况下,在电压和电流采集过程中干扰量会发生急剧波动从而带来测量误差;另外干扰法要求干扰源要足够大,否则零序电压和零序电流容易被系统噪声掩盖,导致难以准确检测。

3.6 大电流法仿真结果

设定干扰线路与被测线路平行架设部分的长度为30 km的情况下,通过改变被测线路的信噪比大小以及干扰电压大小,得到被测线路的零序阻抗测量结果及误差如表2所示。

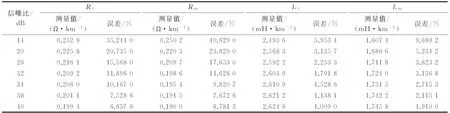
表2 不同信噪比下零序阻抗测量结果及相对误差Table 2 Measurement results and relative errors of zero sequence impedance under different signal-noise ratios

由表2可知,随着测试电源信噪比的增大,测量误差在逐渐减小。由于通过提高被测线路上测量电源的信噪比只能减小干扰对测量结果的影响,本质上并没有消除干扰,因此在干扰保持不变时,其测量误差主要与测试电源的信噪比大小有关,并且任何原因导致的干扰增大都会使测量精度降低。另外由于施加在被测线路上的测量源容量有限,因此大电流法的信噪比一般设置为20 dB左右,相比于其他抗干扰方法,其抗干扰能力比较有限。

4 各抗干扰方法的分析对比

在分析了各抗干扰方法误差产生的原因后,为进一步对比各抗干扰方法的测量精度,设立了两种干扰环境对上述5种抗干扰方法进行对比,通过仿真得到两种干扰环境下相对较好的抗干扰方法。

4.1 干扰线路与被测线路的耦合由弱变强

线路模型见附录A图A3,其理论参数见附录A表A1和表A2,干扰线路的电压等级是110 kV,干扰线路上的变压器零序阻抗均为30 Ω。

改变干扰线路的长度,用上述5种抗干扰方法分别进行测量,其中增量法的增量选取为100 V,大电流法的信噪比设置为26 dB。

线路零序自阻抗和零序互阻抗的仿真测量相对误差对比如图4所示。

图4 不同干扰线路长度下零序阻抗测量相对误差Fig.4 Relative errors of zero sequence impedance under different lengths for interference line

由图4可以看得出如下结论。

1)随着干扰线路长度的增大,即被测线路与干扰线路的互阻抗逐渐增大时,各抗干扰方法的测量误差也逐渐增加。

2)异频法受线路上变压器的零序阻抗的影响,因此测量误差较大,从图中可以看到,当干扰线路长度为80 km时异频法的自阻抗测量误差达到了11.13%。同样地,大电流法在测量时并未消除干扰信号,因此这两种方法的测量结果较其他三种方法的误差要大,在干扰线路长度超过60 km时,其误差超过了20%。

3)从测量结果上看,增量法的抗干扰测量效果最好,其次是干扰法和倒相法,但是在使用增量法时,增量的设置不能太大。干扰法和倒相法的测量误差基本一致,但是由于倒相法的测量步骤很多,调试起来也比较麻烦,因此干扰法要略优于倒相法。

综上,在被测线路附近存在较多运行线路耦合或者耦合较大时,推荐使用增量法测量输电线路的零序阻抗参数。

4.2 干扰信号时刻在变化

线路模型见附录A图A3,其理论参数见附录A表A1和表A2,干扰线路的电压等级是110 kV,干扰线路上的变压器零序阻抗均为30 Ω。

改变干扰线路的输入电压来模拟干扰信号的变化,即在不同测量方式下进行电压和电流信号的采集时,被测线路上的干扰大小是变化的。同样地,用上述5种抗干扰方法分别进行测量,线路零序自阻抗和零序互阻抗的仿真测量相对误差对比如图5所示。

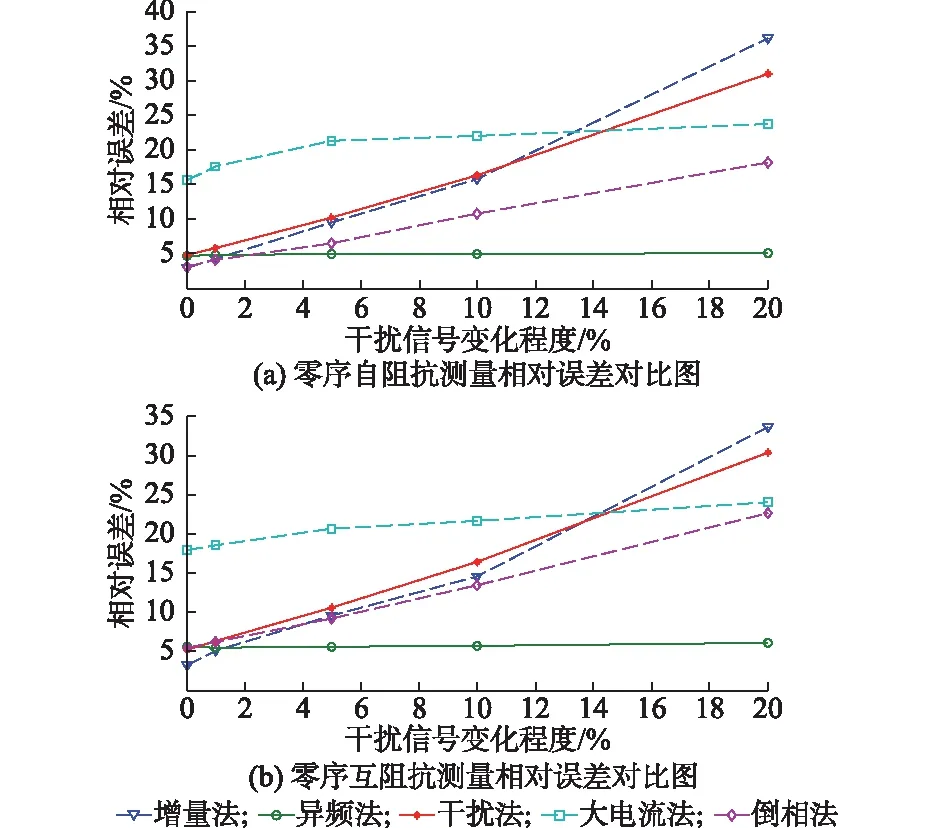
图5 不同干扰信号变化程度下零序阻抗测量相对误差Fig.5 Relative errors of zero sequence impedance under different change levels for interference signal

由图5可以得出如下结论。

1)当干扰发生变化时,增量法、倒相法、干扰法以及大电流法的误差均迅速增大,在干扰改变达到20%时,以上4种方法的测量误差超过了20%,其中增量法的误差最大,自阻抗误差达到了36.12%,互阻抗误差达到了33.53%。这是由于这4种方法都是使用工频信号进行线路参数的测量,而由干扰线路产生的干扰信号几乎都是工频信号。因此当干扰信号发生改变时,在被测线路上采集到的电压和电流信号中的干扰分量也相应发生改变,导致在计算线路的阻抗参数时,其中的干扰量难以消掉,从而产生很大的误差。

2)异频法由于滤除了被测线路上的工频信号,因此工频干扰量发生改变对被测线路上采集到异频电压和电流信号几乎没有影响,因此测量误差与干扰信号不变时的测量误差保持一致,在干扰变化的过程中零序自阻抗测量误差最大为6.1%,互阻抗测量误差最大为5.2%,在可接受的范围内。

综上,在被测线路上的干扰不稳定,变化较大时,推荐使用异频法测量输电线路的零序阻抗参数。

5 测量仪器分辨率对测量方法的影响

5.1 被测线路中的部分线路为运行线路

对运行中的输电线路零序参数进行测量时,通常是通过该线路上的电流互感器和电压互感器获得电流和电压信号。另外由于需要考虑到电流互感器以及电压互感器的变比以及测量仪器分辨率等因素,因此施加在被测线路上的零序电流需要足够大,但耦合到运行线路上的零序电流不能超过该线路零序保护装置的整定值,以免造成保护的误动作。

以LVQB-126W2型110 kV SF6 测试用电流互感器的参数为参考,对被测量线路的测量信号进行估算。以同塔双回线路为例,其模型图如附录A图A7所示,其中线路A停电加压,线路B带电运行,假定线路A,B每一相的零序自阻抗为1.2 Ω/km;线路A,B的零序互阻抗Zm为0.6 Ω/km,长度为100 km。

当线路A上施加10 A的零序电流时,那么线路A上的零序电压为UA=IAZA=400 V;在线路B上的互感电压为Ug=IAZm=200 V;线路B上的互感电流为Ig=Ug/ZB=5 A。

若线路B上的电流互感器使用的变比为600/5时,那么该电流互感器二次侧测量出的电流Ig′=41.7 mA。

若电流互感器使用的变比为1 200/5时,那么该电流互感器二次侧测量出的电流为Ig′=20.8 mA。

由以上计算过程可以得知,在使用增量法测量线路零序参数时,对于以上线路模型,当在线路A前后两次施加的电压增量为100 V时,在线路B电流互感器二次侧测量出的电流增量值为10.4 mA,因此只要测量仪器的分辨率大于1 mA,那么由测量仪器精度引起的测量误差影响会很小。

由GB 1208—2006电流互感器标准可知,对于0.2 s准确级的电流互感器,在测量电流为额定电流的1%时,其测量误差为±0.75%。当线路B上电流互感器使用的变比为600/5时,若想使线路B上的互感电流大小达到额定值的1%,即Ig=Ug/ZB=6 A,由此可以算出线路A上施加的电源电压为480 V。

由以上计算结果可以看出,对于上述线路模型在用各抗干扰方法进行参数测量时,在被测线路上施加的测量信号应大于480 V,从而尽可能地减少仪器测量分辨率导致的测量误差。

另外对于异频法,由于异频信号源的容量一般明显小于其他测量方法使用的工频信号源,因此如果要保证被测线路上的异频信号足够大,那么异频信号源的容量要足够大,否则会因测量信号过小,产生由测量仪器分辨率引起的测量误差。

5.2 被测线路均为停电线路

对停电的输电线路进行零序参数测量时,通常不采用线路上的电压互感器和电流互感器采集信号,而是通过测量仪器自带的或外加的电压互感器和电流互感器获得线路电压和电流信号。由于外加的电压互感器和电流互感器的变比较小,因此输出的二次侧信号较大,不需要考虑5.1节中讨论的测量仪器分辨率影响以及线路保护装置整定值对施加的测量信号的大小要求。但需要对外加的电压互感器和电流互感器的精度提出要求,需选用0.5级以上的测量用互感器。

6 结语

本文对现有5种输电线路零序阻抗参数抗干扰测量方法进行了误差来源分析和仿真,并设置了两种典型的干扰测量环境对这5种抗干扰方法进行了仿真比较,得到以下结论。

1)在被测线路附近存在较多运行线路耦合或者耦合较大时,干扰基本不变或变化不大时,增量法的测量效果最佳,其次是干扰法和倒相法。另外在使用增量法进行线路参数测量时,对于增量的选取,应在满足设备分辨率的基础上尽可能小。而对于干扰法,则需要工频干扰源足够大,否则被测线路上的零序电压和零序电流容易被系统噪声掩盖,导致难以检测。

2)在被测线路周围的干扰变化很大时,推荐使用异频法进行测量。本文仿真发现异频法受干扰线路上的变压器零序阻抗的影响较大,且变压器零序阻抗越小,测量误差越大。另外异频法不能测量长度较长的线路,否则会因测量信号过小,导致因测量仪器分辨率引起的测量误差。

3)除大电流法以外,其他4种抗干扰方法的测量精度受干扰线路自身电流大小的影响很小,但被测线路与干扰线路之间的互感大小对5种方法的测量结果的有较大的影响。

本文主要分析了各抗干扰方法对线路零序阻抗参数的测量误差情况,但是线路的参数还包括电容参数以及线路的正序参数,下一步的研究工作会分析比较各抗干扰方法在线路电容参数以及线路正序参数的测量效果。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。