基于电压下垂控制的含MMC直流电网潮流计算方法研究
张朝学, 邹晓松, 余梦天, 朱余林, 高志鹏, 李芷萧
(贵州大学 电气工程学院,贵州 贵阳 550025)
0 引言
近年来,柔性互联配电网以其灵活可控、适应性强等特点成为现在电力系统研究的热点之一。相对于交流系统,柔性互联系统在远距离输电、分布式能源接入、海底电缆长距离输电等方面有突出的优势[1]。为此,一种新颖的采用电子器件构成的多个子模块串联组成的模块化多电平换流器(Modular Multilevel Converter,MMC)逐渐发展起来,此器件在一定程度上克服了2电平或3电平拓扑VSC换流器的诸多缺陷,如电磁干扰、动态均压等,目前获得了国内外学者、工程技术人员和科研工作者的高度关注[2,3]。然而,MMC-MTDC直流电网的研究应用面临着许多挑战,在系统仿真、控制保护以及大规模混合系统潮流控制等方面还有待深入研究,其中含MMC换流站直流系统稳态潮流计算是其研究的重要基础和前提。
含电压换流器的交直流混合系统潮流计算已经取得了一定的研究成果:文献[4,5]给出了一种含VSC换流器交直流混合潮流计算的数学模型,并提出了一种混合系统潮流的交替求解算法。文献[6]详细分析了含VSC-HVDC的风电场并网技术,阐述传统混合潮流计算方法存在的问题,最后提出了一种含VSC换流器混联系统的潮流解耦算法。文献[7]首先分析了MMC等效模型,提出了含PCC电压下垂控制策略。
上述研究大多都是基于2电平或3电平VSC拓扑的交直流混合电网、交直流混合系统的交替迭代等,很少单独考虑直流系统控制策略下含MMC的直流电网潮流计算,然而直流控制策略下,含MMC的直流电网潮流计算逐渐成为研究的前提和基础。因此,在国内外研究成果的基础上,首先分析了模块化多电平换流器MMC的拓扑结构、模型等效简化处理,然后详细阐述了含MMC的直流电网电压下垂控制策略,在此基础上推导出了基于电压下垂控制的MMC直流电网潮流计算方法。以含恒功率直流负载、直流光伏电源以及采用电压下垂控制策略的7端MMC-MTDC直流系统为例,分别求解给定条件下电压下垂控制的稳态潮流和系统发生波动后电压下垂控制的稳态潮流,最后通过两种运行状态稳态潮流结果的比较分析,得出电压下垂控制策略是有效的,从而验证了本文所提基于电压下垂控制的含MMC直流电网潮流计算方法的正确性。
1 MMC-MTDC直流电网等效模型
1.1 MMC的拓扑结构及其等效处理
模块化多电平换流器是由一系列子模块(Sub-Module,SM)串联构成[8], 如图1所示。

图1 MMC拓扑结构示意图
每个MMC包含6个桥臂,MMC每个桥臂共有2n个SM,上、下桥臂各由n各相同的SM和一个电抗L串联组成,Udc为直流侧电压。
单个SM如图2所示,由上、下2个IGBT(如图2中的S1、S2)和直流电容C组成,D1、D2为反串联二极管,Usm为稳定运行时SM的输出电压,Uc为SM电容电压。
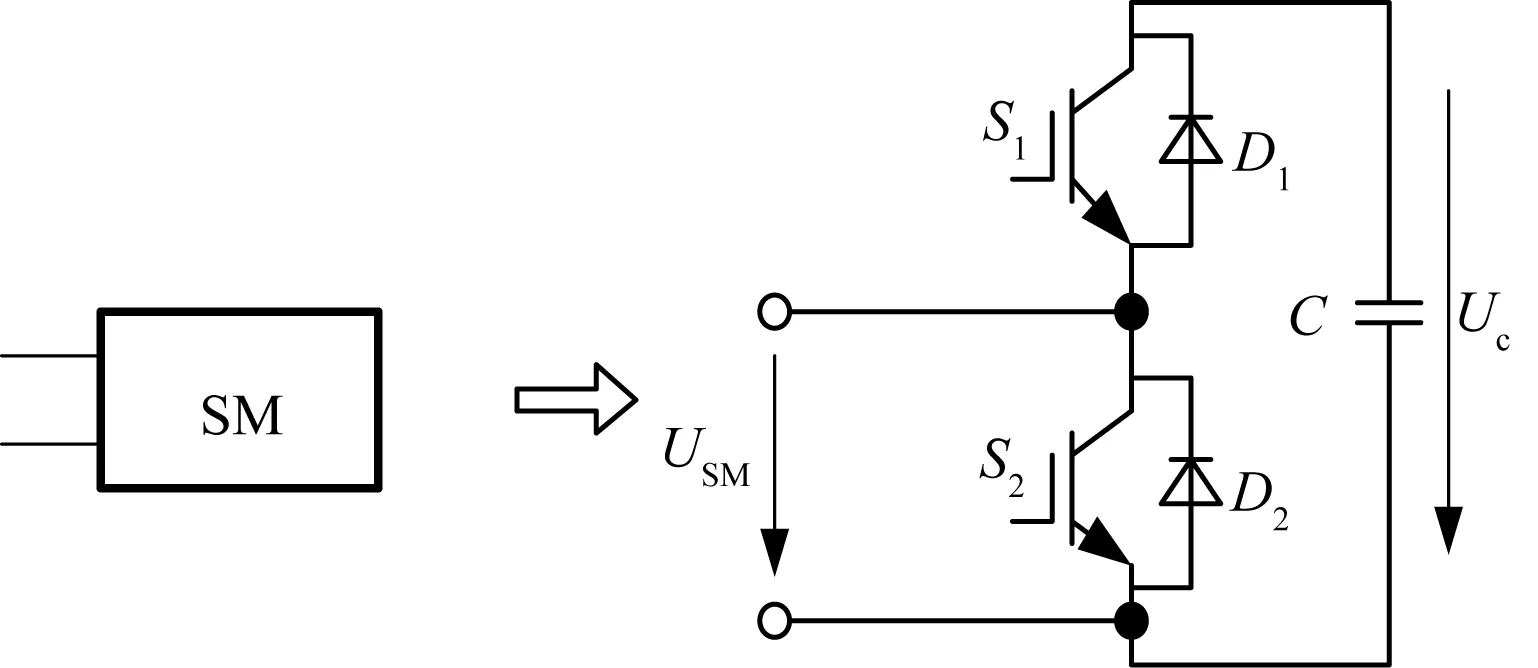
图2 MMC的单个SM拓扑结构示意图
MMC每个桥臂有2n个子模块,最多可以输出2n+1种电平,三相总共有(2n+1)3种电平输出状态,每种电平状态对应一个输电电压。
基于电路理论中的平衡桥同电位点理论[9,10]:同电位点进行短接处理时,既可等效简化电路拓扑,又不改变电路中的电压电流关系;MMC的6个桥臂分别用一个可控的电压源等效,如图3所示。

图3 单端MMC的等效电路模型
任意电压源均为包含一系列离散电平数组成的电压组合。稳态运行时,通过控制电压实现每相电流为直流的三分之一,并且使每相上、下桥臂的电流相等。由此得到逆变器单相输出电压如图4所示。

图4 单相输出电压
1.2 MMC直流电网等效模型
MMC换流器结构如图5所示。图中交流电网侧采用交流母线公共连接点(Point of Common Coupled, PCC)电压源代替,交流电网经过变压器、滤波器和换流电抗器连接到MMC换流站上,换流站直流侧采用双极接线,并连接到直流母线。

图5 MMC换流站结构示意图
当换流站稳态运行时,仅仅考虑稳态基波分量,忽略电压电流中的谐波分量。图5中,Ps和Qs分别为PCC交流电网侧的有功和无功功率,Qf为滤波器无功,Pc和Qc换流站侧MMC母线的有功和无功功率,Ztf表示换流变压器的等效阻抗,Zf表示滤波器的等效阻抗,Zc表示MMC的等效损耗。Us为交流系统侧PCC节点电压;Uc为MMC母线节点电压;Pc.dc为MMC流向直流系统的直流注入功率[11]。
MMC换流站交流侧采用等效电压源模型,直流侧采用等效电流源模型,如图6所示。

图6 直流电网中MMC换流站等效模型
若选取图6中箭头所示功率方向为正,则MMC换流站的有功功率平衡方程可以表述如下:
Pc.dc=-Pci-P0i
(1)
式中:Pc.dc为直流系统从MMC换流站中吸收的有功功率;-Pci为交流系统注入MMC换流站的有功功率;Pc.loss为MMC换流站的损耗。
根据文献[12],Pc.dc、Pc.loss可以表示为:
Pc.dc=UdciIc.dci
(2)
(3)

2 有功—电压斜率下垂控制策略
MMC由可关断电力电子器件组成,能够灵活地控制换流站与交流系统的相角差δ以及无功变量,进而控制交流系统侧连接点的有功量、无功量和电压幅值。根据换流站控制量的不同组合,得到换流站交流侧和直流侧节点的等效类型,如表1所示。

表1 换流站控制方式及交流侧、直流侧等效处理
直流电网有功—电压下垂控制(又称为电压斜率控制)指选取多个换流站采用有功—电压下垂控制,其余换流站采用定有功控制。电压下垂控制指当直流节点电压下降,则电压下降控制器根据自身特性曲线提高注入网络的有功功率;而当直流节点电压升高时,控制器根据下垂控制特性曲线减少输入网络的有功功率。节点电压下垂控制器和对应的U-P特性曲线如图7所示。

图7 直流电网电压下垂控制器及U-P特性曲线
由图中可以得到下垂控制特性曲线表示为:
Pc.dci-Ppv0i=-(Udci-Upv0i)/ρi
(4)
式中:ρi为下垂系数;(Ppv0,Upv0)为所设定原始运行点的电压和有功功率。
对于其他节点采用定有功功率控制,定有功功率控制器和对应的U-P特性曲线如图8所示。
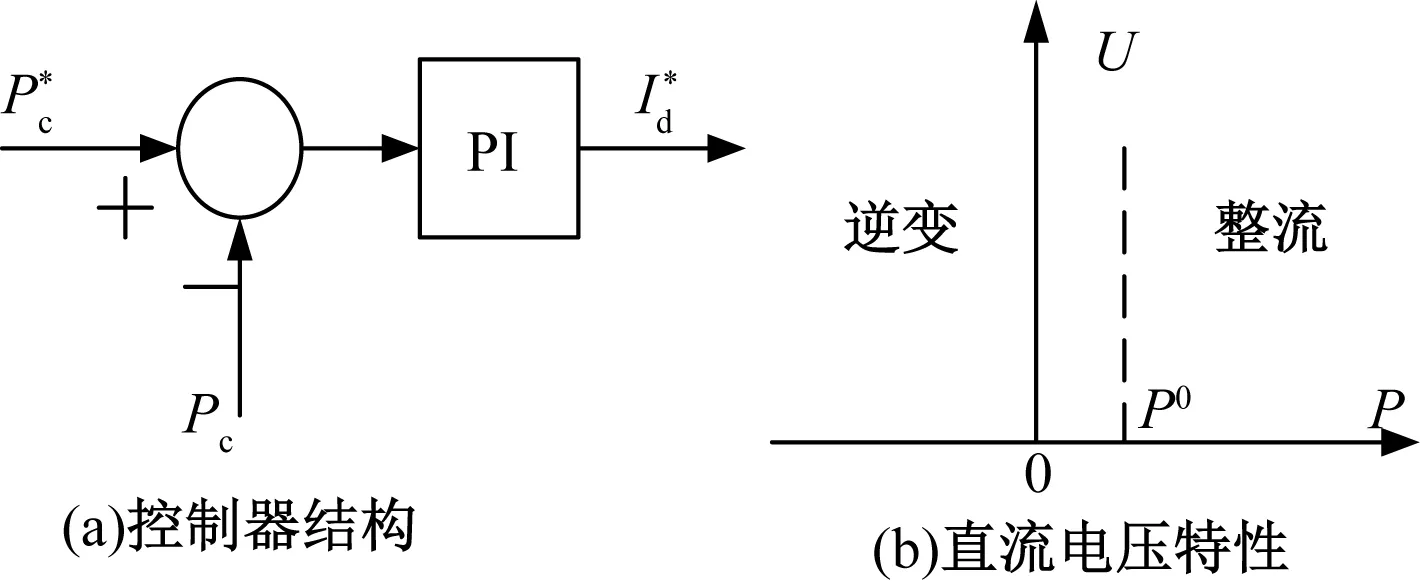
图8 定有功功率控制
3 基于电压下垂控制策略的含MMC换流器直流电网模型与算法流程
由于含MMC-MTDC的直流电网为纯电阻网络,可采用相应的电导矩阵来描述。以注入直流网络的功率方向为正,假设直流电网内共有n个直流节点,则节点电压与电流之间的关系可以用如下方程表示:
(5)
所以,得到节点i的注入功率Pdci为:
(6)
对于节点i的有功功率净值Pschi,按下式计算得到:
Pschi=Pc.dci+PGi-PLi
(7)
综合式(5)~(7),可以得到直流节点i的失配有功功率(也称功率误差):
ΔPi=Pschi-Pdci=(Pc.dci+PGi-PLi)-
(8)
Xi=[Udc1,Udc2,…,Udcn]
(9)
式中:ΔPi为节点i的失配功率;Xi为状态变量;i为直流节点序号(i=1,2,…,n);PGi为节点i直流有功电源发出的有功功率;PLi为节点i直流有功负载吸收的有功功率。
对于含MMC的直流电网电压下垂控制,假设直流电网有n个节点,节点(1~m)采用有功-电压下垂控制(如图7所示);节点(m+1~k)采用定有功控制(如图8所示);其余节点为纯直流节点(没有接MMC换流站或换流站退出运行)。
根据上述推导,可以得出基于电压下垂控制策略的MMC直流电网潮流计算模型如下所示。
当i=1,2,…,m时:
ΔPi=[Ppv0i-Udci/ρi+Upv0i/ρi+PGi-PLi]-
(10)
当i=m+1,m+2,…,k时:
ΔPi=(Pc.dci+PGi-PLi)-
(11)
当i=k+1,m+2,…,n时:
(12)
采用牛顿-拉夫逊法,通过计算雅克比矩阵求出状态变量增量。
(13)
[ΔU](t)=-J-1[ΔP]t
(14)
Ut+1=Ut+ΔUt
(15)
(16)
式中:上角标t表示变量进行第t次迭。
节点电压U为状态变量,失配功率方程ΔPi=0为状态方程组,由此得到求解潮流方程的流程如图9所示。

图9 牛顿-拉夫逊法潮流计算流程图
4 算例分析
为测试所提算法,将算法用于求解含恒功率直流负载、直流光伏电源以及采用电压下垂控制策略的7端MMC-MTDC直流网络如图10所示,采用牛顿拉夫逊法求解网络潮流,并验证其正确性,具体参数见文献[13,14]。

图10 MMC-MTDC7端直流电网拓扑
算例中,电压等级为200 kV。节点1、2为电压下垂控制,其原始运行点及下垂系数(Ppv0,Upv0,ρi)分别为(55 MW,195 kV,5)、(81 MW,210 kV,0.4);节点3、4、5为定有功控制,有功初值分别为-90 MW、74 MW、-120 MW(正功率表示整流站,负功率表示逆变站);节点6、7为纯直流节点,其中节点6引入直流恒流负载20 MW,直流光伏电源10 MW。
应用本文算法对算例进行计算,将算例参数输入MATLAB程序,失配功率误差设为1.0×10-3,得到以下两种运行状态下7端MTDC直流系统稳态潮流分布。
1)电压下垂控制状态1:(系统未波动)
系统稳定状态下,7端MMC-MTDC直流系统节点稳态潮流电压和MMC注入节点功率如表2所示。

表2 直流电网节点电压、功率计算结果
线路发送有功功率、接收有功功率及线路损耗功率如表3所示。

表3 直流电网线路潮流计算结果
2)电压下垂控制状态2:(系统波动后)
当系统运行状态波动,如MMC换流站3(逆变器站)输出功率由原来的-90 MW减少为-80 MW后,根据本文所提算法,系统稳态运行时,得到算例中7端MMC-MTDC稳态潮流结果如下所示。
负荷波动后直流系统节点电压和MMC注入节点功率如表4所示。
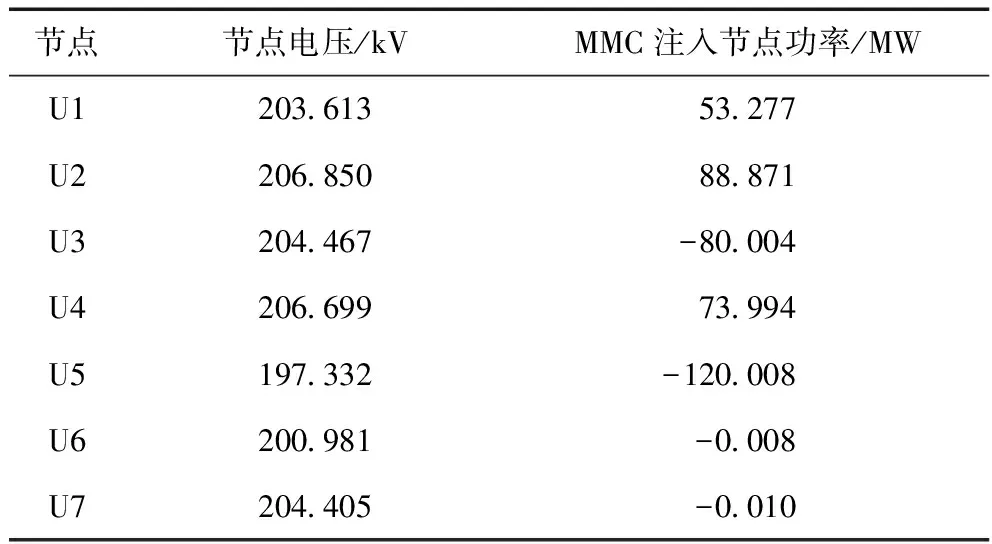
表4 直流电网节点电压、功率计算结果
负荷波动后直流系统线路发送有功功率、接收有功功率及线路损耗功率如表5所示。

表5 直流电网线路潮流计算结果
从上述两种运行状态,稳态电压和MMC注入节点功率的结果(表2和表4)可以看出,由于MMC逆变站3负荷波动,使得系统所有电压发生变化;然而节点4~7的MMC注入功率没有变化,仍然按照给定功率正常运行;为了维持系统稳定运行,节点3负荷波动出现的有功功率差额,完全由下垂控制节点1和节点2进行调节。
图11和图12为下垂控制MMC1、MMC2(节点1、2)的下垂控制曲线。图中有3个运行点,分别为:设定的原始运行点、系统未波动的运行点、系统波动后的运行点。从上述数据计算得出,MMC1的平均下垂系数为4.995,与理论给定值(给定值为5)的误差为0.099%;MMC2的平均下垂系数为0.399 7,与理论给定值(给定值为0.4)的误差为0.075%。

图11 MMC1电压下垂控制曲线

图12 MMC2电压下垂控制曲线
对潮流计算结果进行分析:已知系统波动后给定节点3、4、5的有功功率值为-80 MW、74 MW、-120 MW;由表4的计算结果可知,上述节点给定功率的潮流计算结果为-80.004 MW、73.994 MW、-120.008 MW。经过计算,可以得出节点3、4、5的潮流计算结果误差分别为:0.005%、0.008%、0.007%。
通过上述分析,在误差允许范围内,含MMC直流网络潮流计算结果符合下垂控制特性的约束,即当系统运行状态发生变化时,由电压下垂控制节点1、2按照下垂控制曲线调节直流网络潮流分布。算例结果验证了本文所提基于电压下垂控制的含MMC直流电网潮流计算方法的正确性。
5 结论
在分析模块化多电平换流器(MMC)在国内外研究情况的基础上,通过分析了MMC的拓扑结构、模型等效处理,并详细阐述了含MMC的直流电网电压下垂控制策略,在此基础上推导出了基于电压下垂控制的MMC直流电网潮流计算方法。
以含恒功率直流负载、直流光伏电源以及采用电压下垂控制策略的7端MMC-MTDC直流系统为例,分别求解给定条件下电压下垂控制的稳态潮流和系统发生波动后电压下垂控制的稳态潮流,最后通过两种运行状态稳态潮流结果的比较分析,得出了本文所提方法是正确的。

