旋转电机稳态分析的通用方法
,
(哈尔滨大电机研究所,黑龙江哈尔滨150040)
0 引言
旋转电机稳态分析是电机学的基础内容。传统的分析方法是将各类电机分别进行研究,各类电机都有自己独特的分析系统。例如,对于异步电机,就有T型等效电路分析法、圆图分析法等完备的分析系统,可对异步电机的稳态特性进行有效的分析。这是学者们历经多年做出的卓越贡献。可是,异步电机传统的等效电路与别的电机,例如同步电机,直流电机的有很大差别,相互不能通用。
随着经济与科技的发展,旋转电机在国计民生中的应用越来越广泛,而且,出现了一些新的应用情况。为了便于理解和应用,我们试图从理论上来探讨,寻求一种对于各类电机都适用的稳态分析方法,以便能比较直观地分析各类电机的稳态性能。
通过对旋转电机本质特征的分析,根据机电能量转换过程的原理和旋转电机定、转子电路的耦合关系,可以得出一种旋转电机稳态分析通用的电路模型。其最完备的电路对应于双馈电机;其它各类电机电路模型都可由双馈电机电路模型简化而得。
这一通用分析方法的基本思想是在定、转子之间耦合关系的前提下,将电机实际的定子回路和转子回路分开来分析,并且使之适合于各种类型的旋转电机。
1 旋转电机的基本特征
旋转电机是一种机电能量转换装置;而任何一种机电能量转换装置都是由电系统、机械系统和用作耦合、贮藏能量的电磁场(耦合场)所组成;都有一个固定部分(定子)和一个可动部分(转子)。
机电能量转换过程是电磁场与可动的载流体相互作用的结果。即可动载流体的位移引起磁场能量变化,从而产生电磁力,使部分磁场储能释放出来,变为机械能;同时,磁链变化引起的磁能变化将通过载流体内的运动电势,从电源输入等量的电能,而不断得到补充。这样,通过耦合场-气隙磁场的作用,电能与机械能不断地转换。
由此可见,机电能量转换的关键在于运动电势和电磁转矩的产生;而它们都是通过耦合场—气隙磁场的作用实现的。各类电机电路模型都由双馈电机电路模型简化而得,各电机电路图如图1,图2,图3,图4所示。

图1 双馈电机

图2 异步电机
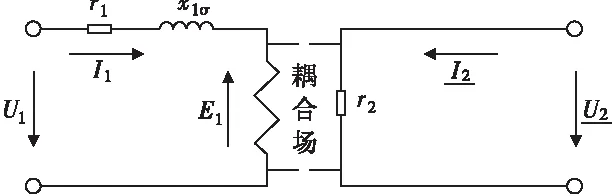
图3 同步电机
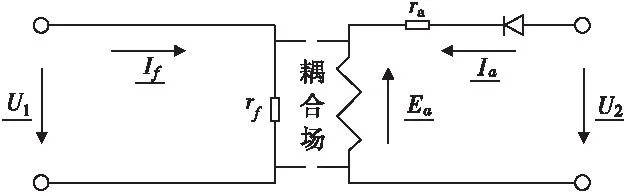
图4 直流电机
所以,建立旋转电机通用电路模型的关键在于如何根据各类电机的特点,正确反映定、转子回路中运动电势和电磁转矩。
实际上,旋转电机通常都有两个绕组,定子和转子上各有一套绕组。转子绕组主要用以产生主磁通,并形成主磁极。定子绕组是主要的载流体,定子绕组对转子绕组有相对运动。由于包括主磁通在内的合成磁通的变化,定子绕组中会连续产生运动电势。当定子绕组中流过电流时,定子绕组与气隙磁场相互作用而产生电磁转矩。这便是旋转电机共同的机理。
通过以上分析,我们不难看出:尽管旋转电机有多种类型,但是,就其本质而言,它们都是由具有相对运动的若干电磁耦合绕组所组成,应该存在着建立稳态分析通用电路模型的可能性。
2 旋转电机的稳态性能
稳态性能是各类旋转电机的基本性能,是最常用的电机性能。电机的稳态性能可以用电机的基本方程,集中参数电路和相量图来描述。
基本方程即电机各回路的电压方程,其中包含了电路的各个参量。集中参数电路能反映电机内部的电磁和机电关系,可用以计算电机的稳态特性。电机相量图则可用以表示电机各回路主要物理量之间的相位关系。集中参数电路是分析电机稳态性能的主要工具。其余两种方法可以由它导出。因此准确构建电机的集中参数电路特别重要。
如上所述,旋转电机都有定子和转子两个部分;而且,它们之间存在耦合关系,形成一个完整的机电能量转换系统。集中参数电路应能准确反映电机内部的电磁和机电过程,反映电机定、转子回路中的运动电势和电磁转矩的形成机制。所以,在构建电机的集中参数电路时应特别注意以下两点。
(1)考虑定、转子耦合关系后,确定电机定、转子回路中各自的运动电势;
(2)准确考虑定、转子回路中,由于导体运动对电路参数造成的影响。
实际上,就是要考虑各回路的运动电势对磁场变化和线圈匝数的关系,以及各回路参数与电流频率的关系,也就是要准确给出实际的定子回路和转子回路的参数。这样,就不再需要先将转子电路归算到定子电路侧;而只要对实际的定子回路和转子回路分别进行计算。对应各类电机不同的电路,可以直接计算出定子和转子回路的实际参数。
这就是本文所提旋转电机稳态分析通用方法的原理。
3 电动机的稳态分析
如上所述,从各类旋转电机的共性出发,依照描述电机稳态特性的一般方法,可以引出旋转电机稳态分析的通用方法。即在计及定、转子通过磁场耦合的前提下,对电机实际的定子回路和转子回路分别进行计算。需要注意的是这里的转子回路处于旋转状态,而非静止状态。
这一方法适用于各种类型的旋转电机。以下,分别对旋转电机的几种主要类型进行讨论。
假设:电机定、转子相数分别为m1和m2
电机定、转子有效匝数比为
电机的转差率为

式中,w1—定子每相串联匝数;w2—转子每相串联匝数;kw1—定子绕组系数;kw2—转子绕组系数;f1、f2—定、转子的电频率。
并假定各类电机均以电动状态为例进行讨论。
3.1 双馈电机
双馈电机是一种定转子均参与机电能量转换的旋转电机[1、2],近年来在新能源和变速系统中得到广泛应用。
3.1.1 集中参数电路
以下用黑体字表示电路各参数的相量。
双馈电机的集中参数电路是所有电机中最完备的,参数最全,可以涵盖其他几种电机的情况,如图1所示。其中
定子电势
E1=-j4.44f1w1kw1Φm
转子电势
E2s=-j4.44sf1w2kw2Φm=E1s/k
式中,Φm—主磁通相量。定、转子电源的频率需满足机电能量转换条件的约束[1]。
3.1.2 基本方程
根据基尔霍夫定律,可以分别得到定转子回路电压方程。
定子回路
U1=I1(r1+jx1σ)-E1
转子回路
U2=I2s(r2+jsx2σ)-E2s
式中,x1σ、x2σ—定子、转子的静态漏抗。
从上面两式可以得出
定子电流
I1=(U1+E1)/(r1+jx1σ)
转子电流
I2s=(U2+E2s)/(r2+jsx2σ)
定子输入电功率
P1=Re(m1U1I1*)=m1U1I1cosφ1;(I*为I的共轭相量)
电磁功率
Pm=Re(m1E1I1*)=m1(U1I1cosφ1-I12r1)
转子输入电功率
P2=Re(m2U2I1s*)
=m2U2I2scosφ2
=Re(m2E2sI2s*)+m2I2s2r2
转子绕组传递功率
Pe2=Re(m2E2sI2s*)
≈sRe(m1E1I1*)=sPm
转子铜耗
Pcu2=m2I2s2r2
机械功率
Pmech=Pm-Pe2=(1-s)Pm
3.1.3 相量图
相量图表示电机定转子回路中电压、电流等相量之间的相位关系,双馈电机的相量图如图5,图中右侧是转子的电压相量图;中间是电流(磁动势)相量图;左侧为定子电压相量图。
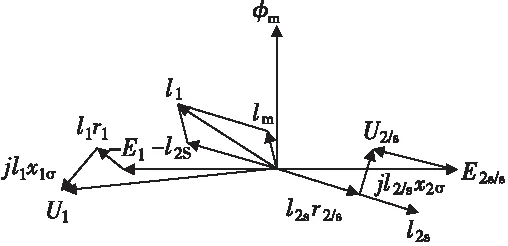
图5 双馈电机相量图
3.2 异步电机
3.2.1 集中参数电路
异步电机的定、转子回路电势与双馈电机相同,但转子回路是短接的;没有连接电源。所以得出异步电机的定转子电路。
3.2.2 基本方程
定子回路
U1=I1(r1+jx1σ)-E1
转子回路
o=I2s(r2+jsx2σ)-E2s
即
o=I2s(r2/s+jx2σ)-E2s/s
可算得
I1=(U1+E1)/(r1+jx1σ)
I2s=E2s/(r2+jsx2σ)
定子输入功率
P1=m1U1I1cosφ1
电磁功率
Pm=Re(m1E1I1*)=m1(U1I1cosφ1-I12r1)
从转子侧看,
电磁功率
Pm=m2Re(E2s/sI2s*)
=m2E2sI2scosφ2/s
=m2I2s2r2/s
转子铜耗
Pcu2=m2I2s2r2
机械功率
3.2.3 相量图
对应于定转子回路的基本方程,可得到异步电机的相量图如图6。
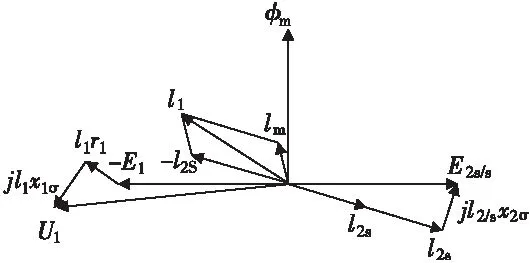
图6 异步电机相量图
3.3 同步电机(以隐极电机为例)
同步电机转子以同步转速旋转。可以把它看成为双馈电机的一种特定运行方式。它的定、转子也都有电能流入,定子通交流电,转子中则为直流电。
同步电机定子的电动势E1由主极磁动势和电枢反应磁动势共同产生,即
E1=E0+Ea
式中,E0—激磁电动势;Ea—电枢反应电动势,Ea可看成是电抗压降的负值,即
Ea=-jI1xa
式中,xa—电枢反应电抗。
3.3.1 集中参数电路
如上所述,同步电机定子回路为交流电路,其感应电势E1为激磁电势E0与电枢反应电势Ea之和;转子回路为直流回路。
3.3.2 基本方程
根据前面的说明,可得同步电机的基本方程如下
定子回路
U1=I1(r1+jx1σ)-E1
或
U1=I1(r1+jx1σ)+jxa)-E0
转子回路
U2=I2r2
以下分别记电机的铁耗和机械耗为PFe,PΩ。
可以计算出
定子输入功率
P1=m1U1I1cosφ1
电磁功率
Pm=m1U1I1cosφ1-m1I12r1
机械功率
Pmech=Pm-PFe-PΩ
转子铜耗
Pcu2=m2I22r2
3.3.3 相量图
在不计饱和前提下,根据基本方程可得同步电机的相量图如图7。
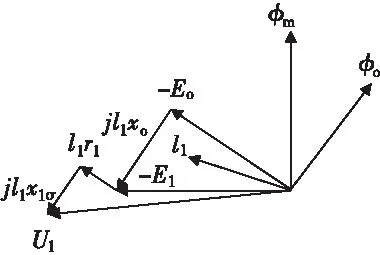
图7 同步电机相量图
3.4 直流电机
3.4.1 集中参数电路
典型直流电机的定子为直流激磁回路。转子(电枢)回路内部为交流电路,经整流后变为直流,所以其集中参数电路可以用图4表示。
其中,电枢的感应电势
Ea=4Nfφm=4Npnφm/60=Cenφm
式中,N—电枢绕组串联匝数;n=60f/p;p—极对数。
3.4.2 基本方程
励磁回路
U1=Ifrf
电枢回路
U2=Ua=IaRa+Ea
可以算得
励磁回路输入
Pf=UfIf=If2rf
电枢回路输入
Pa=UaIa=Ia2ra+EaIa
电磁功率
Pm=EaIa
机械功率
Pmech=Pm-P0=Pm-(PΩ+PFe+Pd)
式中,P0—空载损耗;Pd—附加损耗。
对于直流电机,相量图不再有意义。
这一节按照常用的电机稳态特性的描述方法,利用本文提出的由实际的定子和转子参数构成的集中参数电路可以比较直观地计算各类电机的稳态特性,说明了这种稳态分析方法的可行性和通用性。
4 结语
为了便于理解各类旋转电机的稳态性能,本文提出了一种旋转电机稳态分析通用方法的设想。旋转电机机电能量转换的机理是这一通用分析方法的基础,并使这一方法有可能适用于各类旋转电机。这一方法以双馈电机为分析母本,其它电机均可按照由它蜕化所得的电路进行分析。这是该方法的一个特点。
这一方法直接对各类电机的定子电路和转子电路分别进行分析计算,从而得到定、转子回路实际物理参数,就可对各类电机的稳态性能进行分析。但本文是对这一方法的初步探讨。这一方法的实用性、局限性等问题尚有待于进一步深入研究。

