基于3D的马体尺测量及数据修正方法设计

张婧婧， 李勇伟

(新疆农业大学，新疆乌鲁木齐 830052)

新疆维吾尔自治区是我国传统的养马大区，马的品种资源丰富，据国家品种资源调查显示，目前全疆共有哈萨克马、巴里坤马、焉耆马、柯尔克孜马等4个地方品种，有伊犁马、伊吾马2个培育品种，为全国各省(市、自治区)马品种资源之首。马品种登记是由专门的登记机构依据系谱、体尺外貌、生产性能等资料来划分马的品种，而体尺测量技术是鉴定新疆马品种、推进马良种化进程中不可或缺的技术。

目前，机器视觉的动物体尺测量在国内已经取得一定进展，如利用背景减法和去除噪声算法得到猪体体尺测点[1]；利用背景差分法提取羊体轮廓[2-3]；运用自动阈值分割与形态学处理进行轮廓分割[4]；采用Kinect传感器搭建的羊体尺测量系统，利用彩色、深度图像的多元信息提取羊的体尺[5-6]；基于机器视觉技术测量鱼体侧面积，并将面积与质量进行数据拟合建立模型，评价鱼的质量等[7]。相比国内研究现状，国外对动物体尺进行测度的设备专利较多。测度动物体型，建立结构化专用装置，其优势在于方便图像采集和标定，实现对感兴趣参照点进行线性测量[8-9]，但不足之处在于建立结构化装置成本较高，还必须诱导动物到指定位置。

目前，采用的自动化指标获取方法主要基于二维图像和结构化设施限制动物的位姿来实现获取，对动物的位姿或环境光照和背景要求较严格，在实际生产中难以得到满足，且2D机器视觉技术本身不能获取和动物身体曲面形状相关的指标[10]。

本研究借鉴动物体尺的研究成果，依据新疆马业协会发布的地方标准，利用3D绘图技术，模拟多元线性回归算法，建立了新疆马体尺基础指标的采集模型，旨在完成基于机器视觉的马体尺测量系统的初步设计。

1 机器视觉的马体尺测量方法

1.1 马体尺的测量标准

根据新疆马业协会发布的地方标准，测量马体尺的基本数据，包括体高、体长、胸围、管围，其测量标准为体高：从鬐甲顶点到地面的垂直距离；体长：从肩端到臀端的直线距离；胸围：在肩脚骨后缘垂直绕胸一周的长度；管围：左前管部上1/3处的下端最细处，水平绕其一周的长度。

1.2 测量方法

本设计中，首先应用CINEMA 4D软件设计马体的骨骼，据此建立如图1所示的马体3D模型。在3D图像中，马的体高、体长、胸围、管围指标均属于体尺测量的基础数据，如图1中A—A线、B—B线、C—C线、D—D线所示。基于机器视觉，马体各项指标的测量值必须与图像像素点的坐标距离相关，才具备可测性，而马的体高、体长测量方式符合这一标准。相反，马体的胸围、管围则缺乏坐标的测量依据，因此文中定义了相关指标：胸径、管径如图1中E—E线、F—F线所示(实际坐标分别与C、D点重合)，旨在利用可测的体高、体长、胸径、管径构成马体胸围、管围预测模型的重要参数。

1.3 测量方法的理论依据

测量系统中，马体胸围、管围的预测建立在多元线性回归模型的基础之上。依据多元线性回归理论，因变量与自变量的相关程度越高，回归方程越显著，即获取与胸围、管围相关程度较高的马体尺指标，拟合多元线性回归方程，在方程成立的条件下，预测胸围、管围，即可完成马体尺的有效测量。为此，以20匹焉耆马的体尺数据为依据，在Matlab仿真软件中首先获取马体尺各项指标间线性相关程度的数据。

根据相关系数的标准定义[11]：

r=E{(x-E{x})×(y-E{y})}/(sqrt({(x-E{x})2)×sqrt({(y-E{y})2))。

(1)

式中：E{}为期望值；|r|=1表明两者相关，|r|=0表明两者不相关。

调用Matlab软件中的corrcoef()函数，得到马体的体高、体长、胸围、管围、胸径、管径间线性关系的数据，如表1所示。

由表1可知，焉耆马的体高、体长、胸围、管围、胸径、管径指标之间满足两两线性相关条件，具有不同程度的相关性。利用体高、体长、胸径、管径的优化组合构成方程的自变量，通过回归方程的检验参数评估方程的显著性，即可搭建胸围、管围的预测模型。

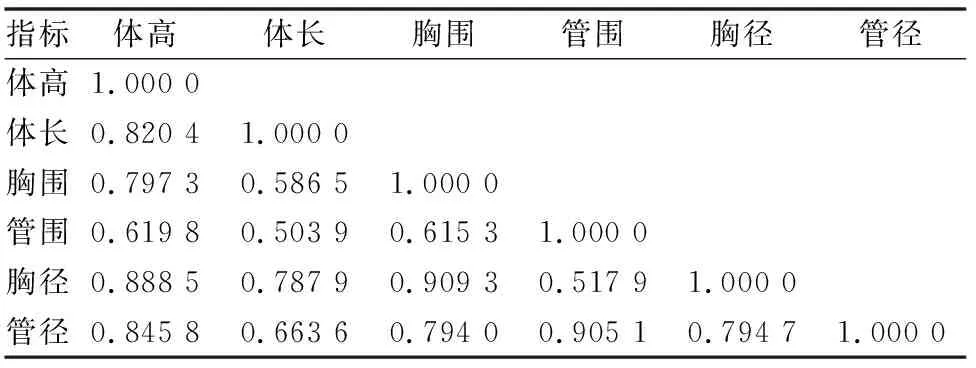
表1 马体尺指标间相关系数

2 体尺测量系统的关键技术

2.1 3D图像的轮廓提取

在基于CINEMA 4D软件设计的马体骨骼中，为精准获取像素点的坐标距离，先进行3D图像的轮廓提取。仿真中，采用Sobel算子的边缘检测算法[12]提取马体轮廓。首先将马体图像变为灰度图，然后分别利用Sobel垂直方向模板和水平方向模板对转化的灰度图像做卷积，求得垂直方向和水平方向梯度，将2个梯度相加即可求得整个图像的梯度，即为图像的轮廓(图2)。

由图2可知，3D马体图像的边缘清晰，图像中动物体色与选取的背景色差虽不明显，但轮廓提取依然较准确。鉴于图像边缘检测的多样化，还同时尝试该图像的一维Canny算子、Robinson算子以及二维Laplace算子[13]的边缘检测。较其他算法，Sobel算法边缘检测的运算速度快，对3D骨骼刻画地较为精准，具有测量优势。

2.2 建立体尺预测模型

基于上述体尺测量的设计方案，首先建立胸围的预测模型。由表1可知，与胸围相关性较高的指标依次为胸径、体高、管径；设计中以20匹焉耆马的胸径、体高、管径为自变量x1、x2、x3，以胸围为因变量y，建立多元线性回归方程，如公式(2)所示。

y=-129.357 3+0.019 5x1+2.151 0x2-0.780 9x3。

(2)

公式(2)r2=0.998 6；F=694.097 5；P=9.259 6×10-5。由P值可知，公式(2)的回归模型成立。

同样地，与管围相关性较高的指标依次为管径、体高、胸围；以20匹焉耆马的管径、体高、胸围为自变量x1、x2、x3，以管围为因变量y，建立多元线性回归方程，如公式(3)所示。

y=5.916 3+1.658 6x1+0.035 0x2-0.1x3。

(3)

公式(3)r2=0.998 8；F=820.348 6；P=7.209 4×10-5。由P值可知，公式(3)的回归模型成立。模型的仿真中，调用Matlab的线性拟合函数regress()方法[14]建立回归方程，为了提高预测的准确度，还针对数据进行rcoplot()残差分析，剔除异常点，并利用判定系数测定方程的拟合程度是否符合建模的条件。

2.3 体尺测量系统的可视化界面设计

鉴于系统交互式设计的需要，利用Matlab GUI工具完成系统可视化界面的设计。在GUI工具中，选择的控件包括axes、pushbutton、edit、uitable、text等，其具体功能如表2所示。

表2 交互式界面中控件的主要功能

3 体尺测量系统的修正方法

在机器视觉的动物体测系统中，由于动物体态各异，不可避免地为体尺测量带来很大难度。针对马体站姿不标准的2类情况，本设计提出了相应的修正方法，旨在加强体测系统的测量能力。应用CINEMA 4D软件设计马体骨骼，绘制了同一匹马行走和倾斜站立的姿态，据此模拟2种姿态下马体尺数据的变化规律。

在马体站姿不标准的情况下，须要引入马体尺的另一指标——体质量，以便替换因为站姿不准而无法准确获取的其他参数，重构预测模型。根据建立线性回归方程的需要，以焉耆马为例，首先获取体质量与马体其他指标间相关程度的数据(表3)。

表3 马体质量与其他指标相关程度

3.1 马行走姿态下体尺数据的修正

马体在行走状态下，其体高减小、体长不变、胸径不变、管径不变，如图3所示。首先须要修正体高，即建立体高的预测模型。在马体尺指标相关系数列表中，体高与体长、胸径、管径的相关程度高，即以焉耆马的体长、胸径、管径为自变量x1、x2、x3，以体高为因变量y，建立多元线性回归方程，如公式(4)所示。

y=0.705 6+0.959 8x1-0.489 5x2+3.386 8x3。

(4)

公式(4)r2=0.998 3；F=583.600 0；P=1.200 0×10-4。由P值可知，公式(4)的回归模型成立。

类似地，行走姿态下，剔除体高指标，以马的体质量、胸径、管径为自变量x1、x2、x3，以胸围为因变量y，建立多元线性回归方程，如公式(5)所示。

y=14.283 6+0.154 8x1+2.256 9x2-3.737 1x3。

(5)

公式(5)r2=0.999 0；F=954.500 0；P=5.746 0×10-5。由P值可知，公式(5)的回归模型成立。

同样地，由于体长与管围的相关性较低，以马的体质量、胸径、管径为自变量x1、x2、x3，以管围为因变量y，建立多元线性回归方程，如公式(6)所示。

y=7.228 9+0.014 9x1-0.037 8x2+0.984 9x3。

(6)

公式(6)r2=0.991 9；F=122.670 0；P=1.200 0×10-3。由P值可知，公式(6)的回归模型成立。

综上所述，体测系统基本实现了行走姿态下马体尺各项指标的测量及数据修正。

3.2 马体站姿倾斜时体尺数据的修正

马体相对相机平面倾斜时，呈现出体质量不变、体高不变、体长变小、胸径不变、管径变小等体尺变化规律，如图4所示。剔除体长、管径指标，体尺预测模型的有效参数仅有体质量、体高、胸径3项指标，据此预测了马体站姿倾斜时体尺数据模型。

以马的体质量、体高、胸径为自变量x1、x2、x3，以体长为因变量y，建立多元线性回归方程，如公式(7)所示。

y=4.794 0-0.060 7x1+1.246 2x2-0.232 7x3。

(7)

公式(7)r2=0.999 8；F=5 474.500 0；P=4.190 0×10-6。由P值可知，公式(7)的回归模型成立。

同样地，以体质量、体高、胸径为自变量x1、x2、x3，以胸围为因变量y，建立多元线性回归方程，如公式(8)所示。

y=-112.923 8+0.009 8x1+1.825 8x2+0.366 2x3。

(8)

公式(8)r2=0.995 0；F=199.650 0；P=5.964 0×10-6。由P值可知，公式(8)的回归模型成立。

再以体质量、体高、胸径为自变量x1、x2、x3，以管围为因变量y，建立多元线性回归方程，如公式(9)所示。

y=7.119 5+0.028 7x1-0.020 4x2+0.069 1x3。

(9)

公式(9)r2=0.999 8；F=4 182.450 0；P=6.273 6×10-6。由P值可知，公式(9)的回归模型成立。

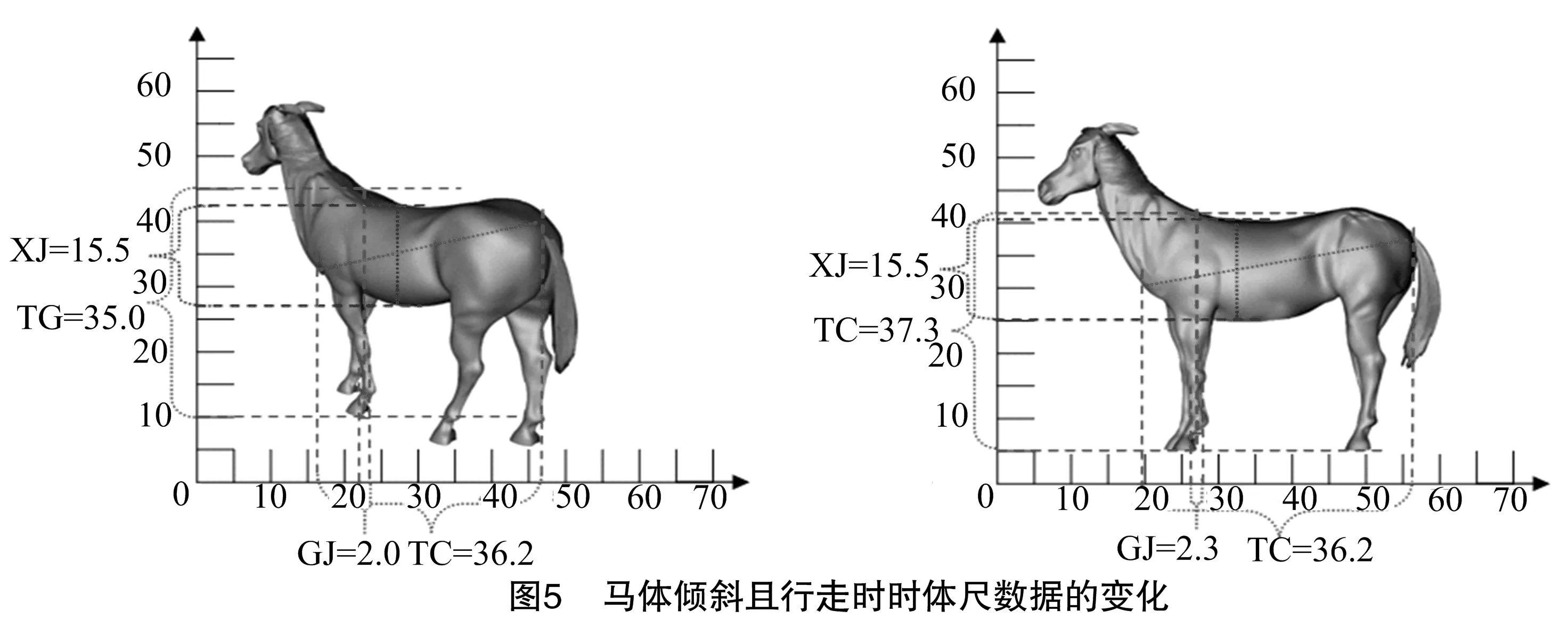
综上，本设计完成了站姿倾斜时马体尺各项指标的测量及数据修正。然而由于马的姿态变化不定，当马体倾斜且行走时，呈现体质量不变、体高变小、体长变小、胸径不变、管径变小等规律，如图5所示，在剔除变化的指标后，其体尺预测模型的自变量不足，体测误差难以控制在有效范围内，因此不再对该模型进行体尺分析。

4 马体尺测量系统的设计与初步测试

4.1 系统的设计流程

基于Matlab开发平台，测量马体尺须要依次完成的轮廓提取、坐标定位、距离测量、数据修正、回归分析、预测值显示、数据保存等步骤，其具体流程如图6所示。

4.2 系统的初步测试

以马体3D图像的体尺数据为依据，在可视化界面中进行系统的初步测试。由图7可知，受面板尺寸的限制，测量中获取体长、体高与胸径、管径数据分别置于2副图像轮廓中操作，降低了坐标定位过程中重复操作的可能性；系统仿真中用红色文本显示马体坐标，并将有效坐标用虚线连接，直观呈现体高、体长、胸径、管径的测量数据，并将所有测量结果显示于edit文本框中。

在马体站姿不标准的情况下，还设计了数据修正按键，用于启动重构的预测模型，修正体尺数据预测结果，降低模型测量的2次误差。

5 结语

基于Matlab开发平台，依据线性相关及线性回归理论，本系统初步完成了马体的体长、体高、胸围、管围的测量。为了加强预测模型的准确性，定义了与图像中像素点距离成比例的胸径、管径指标，且引入了体质量指标，使得线性回归方程的拟合程度增强，回归特性显著。对于站姿不标准造成的测量误差，讨论了2种特定姿态下的修正方法，初步降低因站姿不标准造成的测量误差，具备借鉴意义。

仿真的不足之处主要在于线性相关分析和线性回归方程均取决于少量马体尺的样本数据，据此构建的模型，其测量误差无法定量估算。