基于DPC-GMM算法的船舶燃油系统故障诊断

魏一，张跃文，李斌

大连海事大学 轮机工程学院，辽宁 大连 116026

0 引 言

船舶燃油系统作为船舶的核心动力装置，通过燃油系统各个组件间的协作，将雾化好的燃油输送至设备的喷油入口。燃油系统故障类型繁多，故障导致的重大事故屡见不鲜，并且传统的故障诊断方法无法满足现代化的需求［1-2］。因此，及时、准确地诊断船舶燃油系统异常，判断和识别船舶燃油系统故障十分重要。

目前船舶燃油系统的故障诊断研究主要集中于2个方面：一是基于专家的定性故障诊断方法研究，一般通过专家经验判断故障指标，推理路径清晰，便于用户参与，但是难以处理复杂的、数据量大的诊断对象，不适用于数据驱动情境下的研究［3］；二是基于模型的定量故障诊断方法研究，一般借助机器学习算法，基于数据特征对故障参数进行诊断，常用的故障诊断方法包括反向传播（Back Propagation，BP）神经网络［4］、支持向量机（Support Vector Machine，SVM）［5］等。上述传统算法能够满足对数据的有监督（需要人工标注训练样本类型）诊断［6］，但无法实现船舶燃油系统的故障自动诊断，泛化能力较差。

高斯混合模型（Gaussian Mixture Model，GMM）算法是一种基于非参数的概率性方法，可以根据不同的历史数据自适应训练获取模型参数，对于不同类型的数据集有较好的灵活性［7］。GMM算法能够很好地解决需人工标注训练样本导致的成本增加［8］、泛化能力差的问题，实现无监督的故障诊断过程，极大地提升故障诊断的效率。同时，为了进一步增加GMM算法的精度，引入了密度峰值聚类（Density Peaks Clustering，DPC）算法［9］，以保证观察数据对数似然增大，解决GMM算法存在的局限性。因此，针对已有研究的不足，本文拟提出基于DPC-GMM算法的船舶燃油系统故障诊断方法。针对采集的船舶燃油系统故障模式数据少的特点，首先，采用高斯白噪声对原始数据样本进行扩充；然后，采用本文提出的基于DPC-GMM算法的无监督船舶燃油系统故障诊断方法，基于故障参数智能构建故障诊断模型，进行故障的识别。以期实现对船舶燃油系统不同工作状态的准确判断，为船舶燃油系统状态的监测和故障诊断系统的建立提供新思路和新方法。

1 算法原理

1.1 GMM定义

假设船舶燃油系统状态的训练数据样本X={x1，x2，…，xi}，xi为系统状态量，i=1，2，…，K，K为系统状态类型数目。

GMM是一种描述混合密度函数分布的模型，采用若干个高斯概率密度函数的加权和来描述矢量特征在概率空间的分布状况［10］。即每个高斯混合模型是由K个高斯分布组成，如图1所示，形成不同系统状态的分类器，将这些表征故障类别的高斯分布线性相加，得到GMM的概率密度函数［11］：

式中：Gj(xi|μj，∑j)为系统状态量xi相对于第j类系统状态的高斯概率分布函数，μj和∑j分别是第j类系统状态在X集上的均值与协方差，j=1，2，…，K；αj为第j类系统状态的权重，且满足约束条件

高斯概率密度分布函数表示为

式中，d为描述系统状态特征的维数。

对应的GMM似然函数为

1.2 GMM原理

GMM的基本思想是：首先，使用概率密度函数进行建模；然后，借助期望最大化（Expectation Maximum，EM）算法迭代获取相应参数的最优解，根据正态分布的条件分布获得K个高斯过程函数［12］；最后，对测试样本的船舶燃油系统状态类型值进行计算。

基于GMM的故障诊断是以船舶燃油系统状态数据样本为基础，计算GMM的概率分布，获得K个系统状态，然后采用高斯过程对系统状态数据进行分类，进而进行故障诊断。借助DPC算法，自动聚类获得系统状态数据样本的中心值，以作为GMM的K值输入。

综合式（1）和式（2）发现，构建GMM模型需要的初始参数主要包括K和θ，K值借助DPC算法获得，而参数的常用估计方法是EM算法。

1.3 EM算法的参数求解原理

准确的θ才能构建出高效的GMM分类模型。

采用EM算法逐步迭代来改善θ值的估计。迭代过程中，加大估计参数θ与观测训练样本xi之间的匹配率，使之满足，其中l为迭代次数。逐次迭代得到最优参数值，从而找到使最大的θ*，即

结合式（4）与式（5），通过运算得到

结合式（8）与式（9），可得

其中，当θ=θ'时，J(θ，θ')与P(X，θ)在θ点同时达到极值。综合式（8），说明二者不仅有相同的单调性，极值点也一样。

根据式（7），求偏导为0时对应的θ′值，求解过程分为计算期望（E-step）与计算极大值（M-step）。

1）E-step：数据样本xi属于船舶燃油系统状态类型i的概率，即

2）M-step：使用期望最大化算法求取GMM参数的迭代式，即

假设GMM的参数θ已知，利用E-step对GMM权值进行估计。M-step是基于估计的权值，以优化并确定GMM的参数。重复上述2个步骤直到波动很小，在近似达到极值后结束迭代。

1.4 基于DPC算法初始化的GMM算法

DPC算法是一种基于密度的聚类算法［9］，其基于中心决策图来确定密簇心和类簇个数K，其中K值通过前K个高密度点来判断，然后将非簇心样本点划分到最邻近的峰值密度样本所在类簇，完成样本数据的聚类。DPC具有无需指定聚类参数，能够发现非球类簇并识别噪声点，有益于处理大批量数据的特点［13］。

GMM方法结合EM算法虽然可以保证每次迭代都能使观察数据对数似然增大，但其收敛速度较慢［10］。选定较好的数据初始化结果能够避免这个缺点，并解决参数初始化对GMM方法最终结果造成的影响。

先对输入初始数据进行粗分类，再将EM算法迭代得到的数据作为GMM方法的初始化数据。将DPC算法与GMM算法结合可提高EM算法的收敛速度［14］，从而提高方法的精度，并能从整体上降低模型的时间复杂度。

算法优化过程如图2的伪代码所示。图中，Th是最小误差值。

2 框架模型

本文提出模型的系统框架如图3所示，图中μ为均值，σ为方差。其工作原理分为3个步骤：

1）提取船舶燃油系统状态的特征向量，并采用高斯白噪声对数据样本进行扩充；

2）采用DPC算法初始化船舶燃油系统状态数据类型的数目，对不同类型数据进行GMM模型构建，利用最大似然估计EM算法获取聚类模型参数；

3）利用GMM训练得到测试模型，根据输入的新样本诊断船舶燃油系统最可能的状态。

3 模型构建与仿真实验结果

3.1 船舶燃油系统故障特征的选取

船舶燃油系统故障诊断主要通过高压油管的压力波来体现，当燃油系统中的组件发生故障时，与之相关的特征指标会发生改变。所以，本文选取高压油管的压力波特征进行故障分析。为了获得更好的诊断效果，基于文献［15］，选取8个压力波特征参数，包括燃油喷射最大压力、喷油器启阀压力、次最大压力、波形幅度、上升沿宽度、波形宽度、最大余波宽度以及波形面积（图4）。

对采用40组原始数据的压力波特征的描述性分析如图5所示。

3.2 模型构建

为了增大训练样本的数量，使得建立的GMM更具代表性，将上述特征值分别加上了40，45，50，55，60，65，70，75，80 dB的高斯白噪声，将40组原始数据扩充到了400组。然后再将这400组数据作为训练样本，采用DPC算法寻找数据的最佳聚类中心，以作为EM算法初始化的中心值来构建GMM模型。

通过DPC算法对数据进行聚类，结果表明船舶燃油系统有8种状态（图6）。

DPC算法聚类结果与本文中船舶燃油系统的8种状态一致，如图6所示，状态1～8分别为：正常喷油、75%油量、25%油量、怠速油量、喷油器针阀卡死1、喷油器针阀卡死2、喷油器针阀泄漏、高压油泵出油阀失效［14］。

将DPC算法获取的聚类中心值作为EM算法的初始值来构建GMM模型。

3.3 实验结果分析

GMM模型中，μi为400×8维数据，规模为400×400×8。

在测试阶段，将8组船舶燃油系统故障特征值代入构建的GMM模型中，比较基于对应的每行样本中的数值，数值大的维度代表对应维度的船舶燃油系统状态。得到如下结果：

实验结果如式（13）所示，基于DPC-GMM算法的船舶燃油系统故障识别方法准确率达到了100%，能够准确识别8类系统状态，并且不需要人工标注训练样本，实现了无监督的船舶燃油系统故障识别过程。

采用相同的训练样本和测试样本，运用BP神经网络算法对船舶燃油系统故障进行诊断，设置了5个神经网络隐含层、8个输入神经元、1个输出神经元，最大训练次数为5 000，训练精度默认。测试集输出的结果为[1.81，5.61，3.01，3.05，5.00，5.61，5.61，5.61]，与标注结果[1，2，3，4，5，6，7，8]进行对比，根据式（14），得到正确率为37.5%，故障诊断的准确率较差。

同样，采用SVM方法识别上述船舶燃油系统状态，诊断故障类型。训练采用径向基函数（Radical Basis Function，RBF），对DPC-GMM，BP神经网络和SVM支持向量机算法的实验结果进行了对比，结果如表1所示。

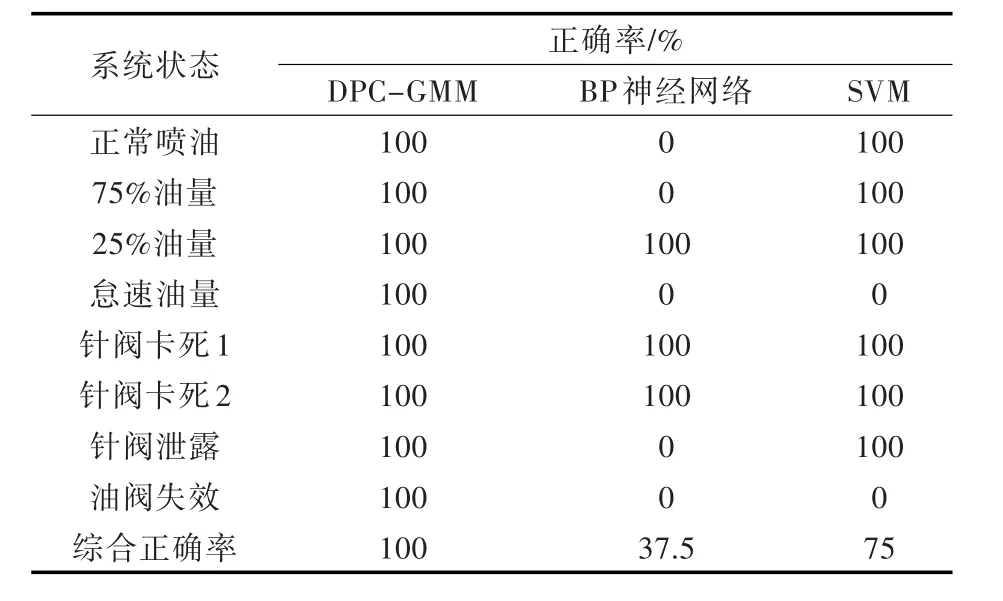
表1 船舶燃油系统状态的识别结果Table 1 Fault diagnosis of ship fuel system

由表1可见，采用DPC-GMM算法对船舶燃油系统进行故障诊断时，其效果明显优于BP神经网络和SVM算法，故障诊断的正确率达100%，所有故障类型都能正确划分，诊断能力较强，解决了常用船舶燃油系统故障诊断方法泛化能力低的局限性。

对常用船舶燃油系统故障诊断方法的训练时间进行对比，同时还对比了直接采用GMM方法的训练时间，结果如表2所示。由表可见，本研究提出的基于DPC-GMM算法的船舶燃油系统故障诊断方法能够实现故障的精准与快速诊断。

表2 船舶燃油系统状态识别模型训练时间对比Table 2 Training time of fault diagnosis model of ship fuel

综合上述研究得出，本文提出的DPC-GMM方法解决了常用船舶燃油系统故障诊断方法存在的识别精度低、收敛速度慢的问题，也解决了GMM算法本身存在的收敛速度慢的局限性。

4 结 语

针对现有研究无法实现船舶燃油系统故障自动诊断、泛化能力较差的问题，本文提出了基于DPC-GMM算法的船舶燃油系统故障诊断方法，根据船舶燃油系统的特征抽取出8个维度的特征向量。构建GMM时，应用DPC算法对船舶燃油系统特征参数进行初始化，使用EM算法进行参数估计，建立完整、高效的故障诊断模型。实验结果表明，本文提出的基于DPC-GMM算法的船舶燃油系统故障诊断方法，诊断准确率可达100%，优于传统的BP神经网络和SVM算法，同时可节约人工标注成本，是一种高效、无监督的故障诊断方法，具有较高的实用价值，也为船舶燃油系统故障诊断问题提供了一种新的方法。