考虑用户响应程度的电动汽车分时电价策略*
周凌锋,王杰
(上海交通大学 电子信息与电气工程学院, 上海 200240)
0 引 言
近年来,为了应对日益严重的环境污染问题和能源短缺问题,电动汽车获得了快速的发展[1-3]。大规模电动汽车接入电网可能会对电网负荷产生冲击,引起电能质量下降[4]。另一方面,由于电动汽车充电具有可断续充电的特点(充电“弹性”),为其充电的优化提供了可能。若有效利用,电动汽车也可以为电网提供诸如削峰填谷,调频等作用[5]。
为了减少电动汽车无序充电对电网造成的损害,近年来,国内外对智能充电调度优化进行了大量研究。文献[6]提出了一种考虑电动汽车分散式充电的最优填谷优化策略,在考虑用户竞争的情况下,有效抑制了峰谷差。文献[7]考虑了电动汽车的充电和放电过程,提出了全局最优和局部最优的充电优化策略。文献[8]将电动汽车作为一个群体,以集群最优削峰填谷为目标提出优化方法。以上文献都是以对电动汽车的直接调度为基本假设,并未考虑用户需求侧对电价等充电信息的响应行为。
电价响应作为需求响应的一种重要形式,以电价为信号引导或改变用户用电方式,达到增加用户收益和利于电网的目的[9],合理的电价机制可以激励电动汽车用户选择合理的时间充放电。文献[10]建立了基于需求响应的电动汽车经济调度模型,优化了充电电价触发值,降低了用户充电成本。文献[11]考虑多目标建模,建立了实时电价下电动汽车车主对电价变化的需求响应模型,并设计了最优分时电价定价方案。文献[12]通过分时电价机制,有效的减少了电网负荷峰谷差。
本文提出了一种在分时电价政策下考虑用户需求响应程度的充电模型。通过建立用户参与电价激励程度模型,运用成本效益分析电动汽车用户总成本。以用户成本最小,电网电价收入最高和负荷峰谷方差最小为目标,通过模糊决策理论和多目标算法NSGA-II求得Pareto解集的折中解。在具体算例中,本文还考虑了政府补贴额对用户响应度的影响。
1 电动汽车充电功率建模
本文主要考虑家用电动车用户的充电行为。开始充电时刻和日行驶里程取决于用户的出行习惯,可通过统计调查数据得到。其中,美国家庭交通出行调查数据(NHTS)是具有代表性的调查数据。分析数据可得,每段行程行驶里程可近似为对数正态分布,概率密度函数为:
(1)
式中d为一天的行程行驶距离;μD为行驶距离期望值;σD为行驶距离标准差。本文中以每段行程距离为分析数据,μD取值3.2,σD取值0.88[13]。
最后一次行程结束时刻,即为开始充电时刻,其概率密度函数可表示为[13]:
(2)
式中t为开始充电时刻;μs=17.6;σs=3.4。
假设电动汽车采取恒功率充电方式,单辆电动车的充电功率为Pc,放电功率为Pdis。电网在时刻t的电动汽车总充放电功率可以表示为:
(3)
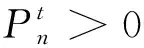
第n辆车在i时刻开始充电的充电时长为:
(4)
式中dn为第n辆车一天的行驶距离,可由式(1)模拟得到;W为电动汽车每百公里耗电量。
2 用户需求响应度定量模型
电价需求响应是通过设置分时电价或者实时电价机制来引导用户在电价低时进行充电,在电价高时进行放电,以赚取差价的行为。峰谷电价差值会影响用户的需求响应比例。用户不是在电价变化所有范围内都愿意改变充电方式,进行电价响应。只有电价变化超过一定范围用户才愿意改变用电习惯,即用户响应存在上下限阈值[14]。基于此,本文提出了如图1所示的用户需求响应度定量模型:

图1 用户需求响应度定量模型
其中Δpfg表示峰谷电价差,λfg表示用户需求响应度,λmax是最大的需求响应度。lfg为用户需求响应启动阈值,即只有当峰谷电价差大于lfg时用户才会参与到电价需求响应中。小于lfg的区域称为死区。hfg为用户需求响应饱和阈值,即当峰谷电价差大于hfg时,需求响应度不再增大,进入饱和区。在lfg和hfg之间的区域是线性区。λfg可表示为:
(5)
3 考虑需求响应的充电优化模型
3.1 目标函数
本文以用户总成本最小,实行分时电价政策后电网电费收入最高和电网总负荷峰谷方差最小为目标,建立了多目标充电优化模型。
3.1.1 用户成本最小
经济性是影响消费者选择汽车类型的重要因素。一般而言,只有当电动汽车使用费用相比传统燃油汽车低廉时,消费者才可能选择电动汽车[15]。因此,本文将消费者使用电动汽车看成一项投资,采用成本收益法来分析用户的总成本。对于电动汽车用户来说,现金流出包括电动汽车购置费、充电费用、电池的损耗等;当电动汽车放电参与电网调度时,产生电费收益为现金流入,用式(6)描述用户成本:
minZ1=Cout-Cin=(C0+Cc+Bm)-Cdis
(6)
式中Z1为用户总成本;Cout表示现金流出;Cin表示现金流入;C0表示购买汽车的成本;Cc表示充电成本;Cdis表示通过放电产生的收益;Bm表示电池损耗费用,与充电次数nb有关。
3.1.2 电力公司电价收入最大化
对电力公司来说,实行分时电价往往会减少电费的收入,所以要让电力公司的电价收入最大化:
(7)
式中ρt为任意时刻t的电价;f(t)为电网t时刻的总负荷;F2表示在实施分时电价后收取的电费。
3.1.3 电力系统负荷波动最小
除了需要考虑用户侧的利益,我们也需要兼顾电能质量。本文将电力系统的负荷波动情况纳入目标函数,可以用式(8)表示:
(8)

(9)
3.2 约束条件
3.2.1 分时电价价格范围约束
设ρ0为分时电价实施前的电价,ρf,ρp,ρg分别表示分时电价实施后峰-平-谷时的分时电价信息。对于任意时刻t的电价ρt满足如下电价范围约束:
ρtmin<ρt<ρtmax
(10)
式中ρtmin和ρtmax分别表示时刻t允许的最低和最高电价信息,由监管部门制定。同时为了使电价分布相对均匀,对电价进行如下约束:
(11)
3.2.2 电力公司获利约束
实行分时电价前后应该保证电力公司不因实施分时电价政策而减少收益。令F1,F2分别表示电力公司在实施分时电价前后收取的电费,S为政府对电力公司实施分时电价的补贴。则需要满足:
F2+S>F1
(12)
其中,各变量满足如下关系:
(13)
政府的补贴政策S与总负荷有关,式(13)中G表示每千瓦时政府补贴的费用。
3.2.3 电动汽车用户获利约束
为了保护电动汽车用户的利益,必须使其实施分时电价前后的充电费用不增加。其约束条件为:
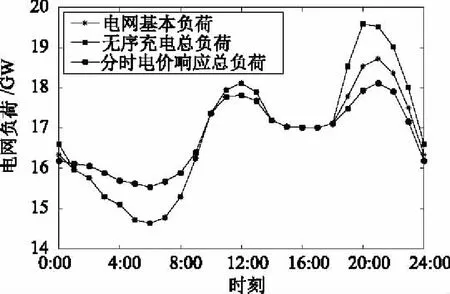
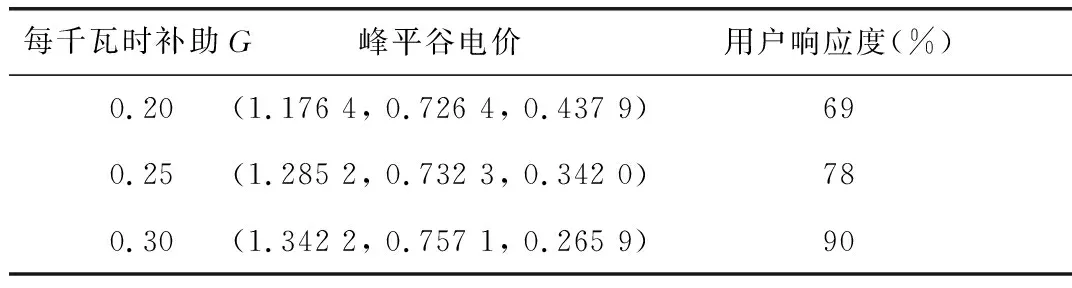
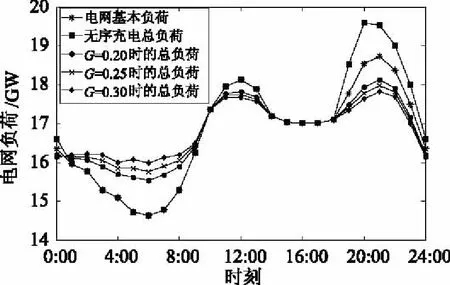
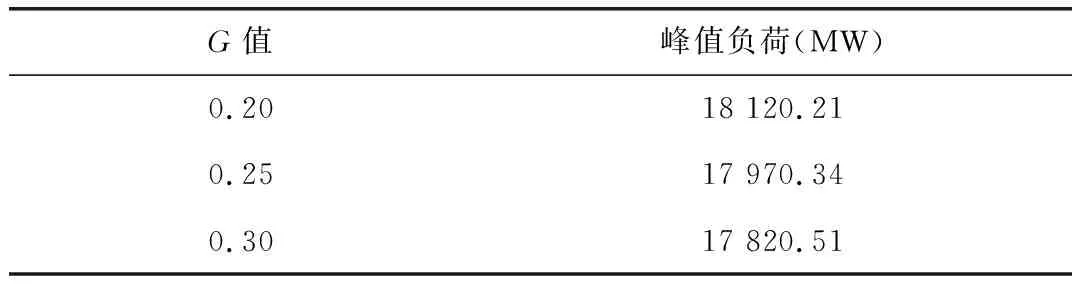
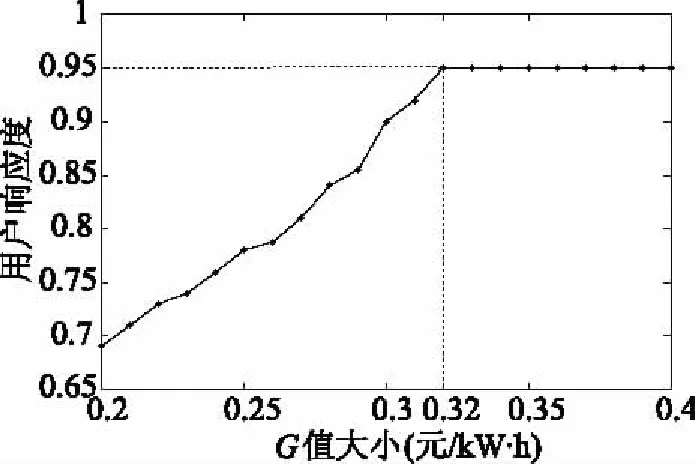
F2 (14) 3.2.4 电动汽车用户获利约束 假设用户只在电网尖峰时段进行放电,由于放电容量不能超过电池余量,电动汽车的放电时长存在约束。放电的最大时长用式(15)表示。 (15) 式中Δtf为峰价时段的时长;Q0表示电池充满电的容量;df为电网放电前的行驶路程;q为每公里的耗电量;Qleft表示放电前电池的剩余电量。 3.2.5 用户需求响应触发约束 由第2章可知,用户对电价需求响应的参与度与峰谷电价差有关,存在触发阈值,故须满足: ρf-ρg≥lfg (16) 同时,对于触发阈值,还需要满足至少要弥补一次充放电电池的损耗费用,可以表示为: (17) 本文采用NSGA-II算法对多目标模型进行优化求解。NSGA-Ⅱ算法是比较高效的解决多目标问题的算法,通过引入精英保留算子,保证了解集的多样性,使得到的Pareto解集分布均匀[16]。 通常,多目标问题是在一组约束条件下,尽量让多个目标达到最优。但是因为各目标之间存在矛盾性,所以只能得到Pareto解集,可以表示为: (18) 式中m表示目标的个数;Q表示等式约束的个数;J表示不等式约束的个数。 对于多目标问题来说,决策者需要从Pareto的解集中选取一个合适的解作为最优解。本文通过模糊理论来求解多目标问题的最优折中解。 由于本文的目标中大部分为最小化目标,故选用偏小型模糊隶属度函数来选取具有最大模糊隶属度的Pareto解,计算方法如下所示: (19) (20) 本文采用一组电网夏季常规负荷数据[17],首先研究了分时电价对于引导用户转移用电时段的影响。进一步,研究了补贴数额对于用户参与响应程度的影响。本文算例中用到的参数设计如表1所示: 表1 算例参数设计 本文将用户的总成本以日为单位进行折算。假设电动汽车的使用年限为10年,则可求得折算到每天的购车费用为54.79元,每次充电折算为4元。对于饱和阈值hfg取1.2元。 在未实施分时电价政策前,用户不会对电价作出响应,充电具有随机性。本文假设所有用户在回到住宅后即开始进行充电,这本质上是一种无序的充电方式。图2显示了无序充电对电网的影响。 图2 无序充电下电网总负荷 可以看出在无序充电下,电网的尖峰负荷由之前的18 520.67MW上升到了19 585.49MW。以图2为基础,本文利用简单的数据移动平均方法给出了峰-平-谷的时段划分,如表2所示: 表2 峰-平-谷电价时段划分 其中表中每个数字表示一个时段,例如11表示时段11:00-12:00。本文设定的计算精度为10-4,每个时段电价用长度为10的染色体来表示。通过对目标函数的求解,可以得到具体的分时电价如表3所示: 表3 峰-平-谷分时电价 由数据可求得此时的响应启动阈值lfg为0.13,峰谷时段电价差为0.738 5。结合用户需求响应度模型可以求得此时的需求响应度为69%。该需求响应度下电网的总负荷如图3所示: 图3 分时电价下电网总负荷 由图3可知,分时电价政策可以很好地激励用户改变用电习惯,将充电时段从电网负荷高峰段转移至低谷段,使得高峰段的负荷得以削弱,低谷段的负荷得以填平,起到了很好的“削峰填谷”作用。 用户响应电价的程度并不是一成不变的,与电价差有关,而分时电价的制定受诸多因素影响,其中政府的补助额G直接影响着电网公司对分时电价的定价。在4.1节中,计算了在G值取0.2元/kW·h时的最优分时电价。计算结果表明,在此条件下,用户需求响应度为69%,依然没有吸引到一部分用户参与到电价需求响应中来。在不牺牲电网公司经济利益的情况下,为了让更多的用户参与到电价需求响应中来,政府需要提供更高的补助额。 表4选取了3组G值分别取0.20,0.25,0.30时的最优分时电价,在该分时电价下,电网负荷如图4所示: 表4 峰-平-谷分时电价 由图4可知,随着G值的不断增大,用户的电价响应程度越高,表5表示了不同图四中的不同负荷曲线的最大峰值负荷。 图4 不同G值下电网总负荷 G值峰值负荷(MW)0.2018 120.210.2517 970.340.3017 820.51 可以看到,随着G值的增大,电网负荷的夹峰值也在随着用户电价响应度的升高而减小,表明分时电价政策可以有效地引导电动汽车用户进行有序充电行为,实现对电网的“削峰填谷”。 进一步,由于用户需求响应度有最大值λmax,故随着G值的增大,存在一个Gmax。在Gmax下,用户需求响应度达到最大;随后G值的增大不会影响用户需求度。本文以0.20为仿真起始值,仿真步长为0.01,得到如图5所示的结果: 图5 不同G值下用户响应度 由图5可知,在一定范围内,随着G值的增大,用户响应度逐渐增大,Gmax的值为0.32,即政府为了鼓励用户最大程度地使用电动汽车进行电价的响应行为,至少应提供给电网公司的补贴为0.32元/kW·h。 (1)本文基于用户对分时电价的响应行为,综合考虑了用户和电网公司的利益,建立了分时电价下的电动汽车需求响应模型。同时建立了用户响应度定量模型,定量地描述用户参与电价响应的程度。运用NSGA-II算法和模糊隶属度求解了算例。算例结果充分显示了分时电价对“削峰填谷”的有效性; (2)针对政府补助额对用户电价响应度的影响进行了敏感度分析。结果显示,在一定范围内,政府补贴越多,需求响应度越好,对负荷的“削峰填谷”作用越好。同时为了使用户需求响应度达到最大,定量地求得了最小的政府补助额; (3)对于电价响应度模型,本文的建模相对简单,在今后可以进行更加合理化的建模。同时对用户而言,除了经济性因素,对充电方式和时段也存在满意度的问题,在今后研究中需要综合考虑。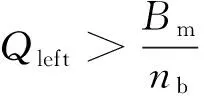
3.3 模型求解算法

4 模型算例求解

4.1 分时电价的最优定价



4.2 政府补助额对响应度的敏感度研究
5 结束语

