浅海牧场式围栏设施中柱桩波流力计算方法比较

王 刚，孙一艳*，雷 鹏，王占行，马玉莲，丁 磊

(1.中国水产科学研究院渔业工程研究所，北京 100141；2.天津科技大学 海洋与环境学院，天津 300457)

近年来，国家大力推进生态健康养殖，鼓励发展海洋牧场[1-3]立体养殖和外海深水抗风浪网箱养殖等生态健康养殖模式。浅海牧场式围栏设施符合渔业转方式、调结构的发展方向，是海水养殖结构调整产业升级的重要新兴技术，借助水运桩基的工程经验和铜合金网衣的研究应用成果，有广阔的产业应用前景。目前该模式发展迅速，尤其是在椒江大陈岛海域大型牧场式浅海围栏设施以及大黄鱼生态放养模式的创新发展方面起到了很好地应用效果。

目前，围栏设施柱桩所处水深大、自由长度高,主要承受水平力，对抗弯要求高，故一般采用预应力砼管桩和钢管桩。波流力是柱桩所受的主要荷载[4]，直接影响着桩基的型式和断面尺寸，对柱桩结构的设计安全具有重要的影响[5]。当波流夹角为0时，柱桩所受的波流力数值最大，因此将其作为工程波流力的设计值[6-7]。目前工程设计中常用的两种柱桩波流力计算方法分别为：(1)根据《港口与航道水文规范》[8](JTS 145-2015)第10.3条和《港口工程荷载规范》[9](JTS 144-1-2010)第13章分别计算正向波浪力和水流力，再将二者线性叠加；(2)根据《港口与航道水文规范》[8](JTS 145-2015)第10.4条直接计算正向波流力，此方法考虑了波浪和水流之间的影响。然而，目前关于两种方法计算差异的比较还鲜有报道，这就给工程设计中的方法选择增添了困难，于是，本文将结合椒江大陈岛海域大型浅海牧场式围栏设施工程设计需求，基于以上两种方法，比较不同波浪和水流条件下两者结果差异，分析影响差异的主要因素，为今后浅海围栏设施中柱桩工程设计的方法选择和科学研究提供一定的参考依据。

1 计算方法

围栏设施柱桩一般为D/L≤0.2(D为柱桩的直径，L为波长)的小尺度柱桩，本文将基于此前提条件进行计算。

1.1 方法一

1.1.1 波浪力计算

根据《港口与航道水文规范》[8](JTS 145-2015)第10.3条，作用于整个柱体高度上的正向波浪力由速度分力和惯性分力组成，其最大速度分力PDmax和最大惯性分力Plmax的确定方法如下：

(1)当H/d≤0.2且d/L≥0.2或H/d>0.2且d/L≥0.35时，PDmax和Plmax分别按下列公式计算

(1)

(2)

(3)

(4)

PDmax和Plmax对z1断面的力矩MDmax和Mlmax分别按下列公式计算

(5)

(6)

(7)

(8)

其中：H为波高；d为水深；z1、z2为计算点在水底面以上的高度；γ为水的重度；g为重力加速度；CD为速度力系数，对圆形断面取1.2；CM为惯性力系数，对圆形断面取2.0；A为柱体的断面积，m2。计算整个柱体上的PDmax及其对水底面的力矩MDmax时，取z1=0和z2=d+ηmax；而在计算整个柱体上的Plmax及其对水底面的力矩Mlmax时，取z1=0和z2=d+ηmax-H/2，其中ηmax为波峰在静水面以上的高度。当H/d≤0.2且d/L<0.2或H/d>0.2且d/L<0.35时，可按上述方法计算作用于整个柱体上的正向波浪力，并应对PDmax乘以系数α；对MDmax乘以系数β。α和β可分别查图确定。当0.04≤d/L≤0.2时，尚应对Plmax乘以系数γP，对Mlmax乘以系数γM。系数γP和γM可查图确定。

(2)作用于整个柱体高度上的正向最大总波浪力Pmax和对水底面的最大总波浪力矩Mmax可按下述方法确定：当PDmax>0.5Plmax时，两者分别按式(9)和式(10)进行计算

Pmax=Plmax

(9)

Mmax=Mlmax

(10)

当PDmax>0.5Plmax时，两者分别按式(11)和式(12) 进行计算

(11)

(12)

1.1.2 水流力计算

根据《港口工程荷载规范》[9](JTS144-1-2010)第13章，作用于港口工程结构上的水流力标准值Fw应按下式计算

(13)

其中：Fw为水流力标准值；V为水流设计流速；Cw为水流阻力系数；ρ为水密度，海水取1.025 t/m3；A为计算构件在与流向垂直平面上的投影面积。水流力的作用方向与水流方向一致，当下部构件顶面在水面以上时，其合力作用点位于水面以下1/3水深处。

将上述最大总波浪力和对水底面的最大总波浪力矩分别和对应的水流力和水流力矩线性叠加，即得到最大总波流力和总波流力矩。

1.2 方法二

根据《港口与航道水文规范》[8](JTS 145-2015)第10.4条，作用于水底面以上高度z处单位长度柱体断面上的正向波流力p(z,t)按下列公式计算

(14)

(15)

(16)

(17)

(18)

ωr=ω-kuc

(19)

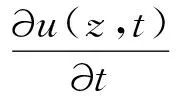
(20)

其中：T为波浪周期，不规则波时取谱峰周期TP。求作用于整个柱体高度上的总波流力Pwc(t)时，沿柱体自水底z=0到波面z=d+η对p(z,t)进行积分，即

(21)

波面在静水面以上的高度η值按下式计算

η=ηmaxcosωt

(22)

从式(21)得到的关于Pwc的时间序列中可以确定最大总波流力Pwcmax。同理，可以通过式(23)确定对水底面的的最大总波流力矩Mwcmax：

(23)

需要说明的是，以上求解过程是借助工程上常用的MathCAD软件编制计算程序完成的。

2 结果分析

2.1 计算工况

结合椒江大陈岛海域大型浅海牧场式围栏设施工程设计需求，确定计算工况如下，围栏设施布置示意图见图1。(1)水深d：10 m；(2)柱桩直径D：1 m；(3)波高H1%：2.0、2.5、3.0、3.5、4.0 m；(4)平均周期T： 5、6、7、8、9 s；(5)流速V：0.5、1.0、1.5、2.0、2.5、3.0 m/s。

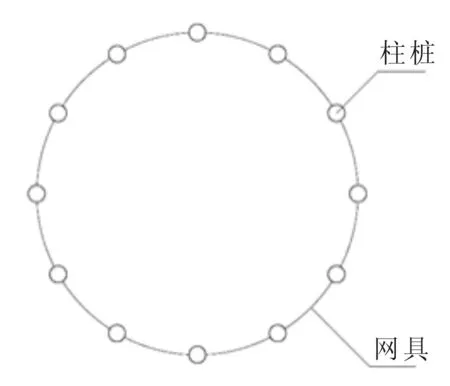
图1 围栏设施平面布置Fig.1 Layout of the fence facilities

2.2 结果分析

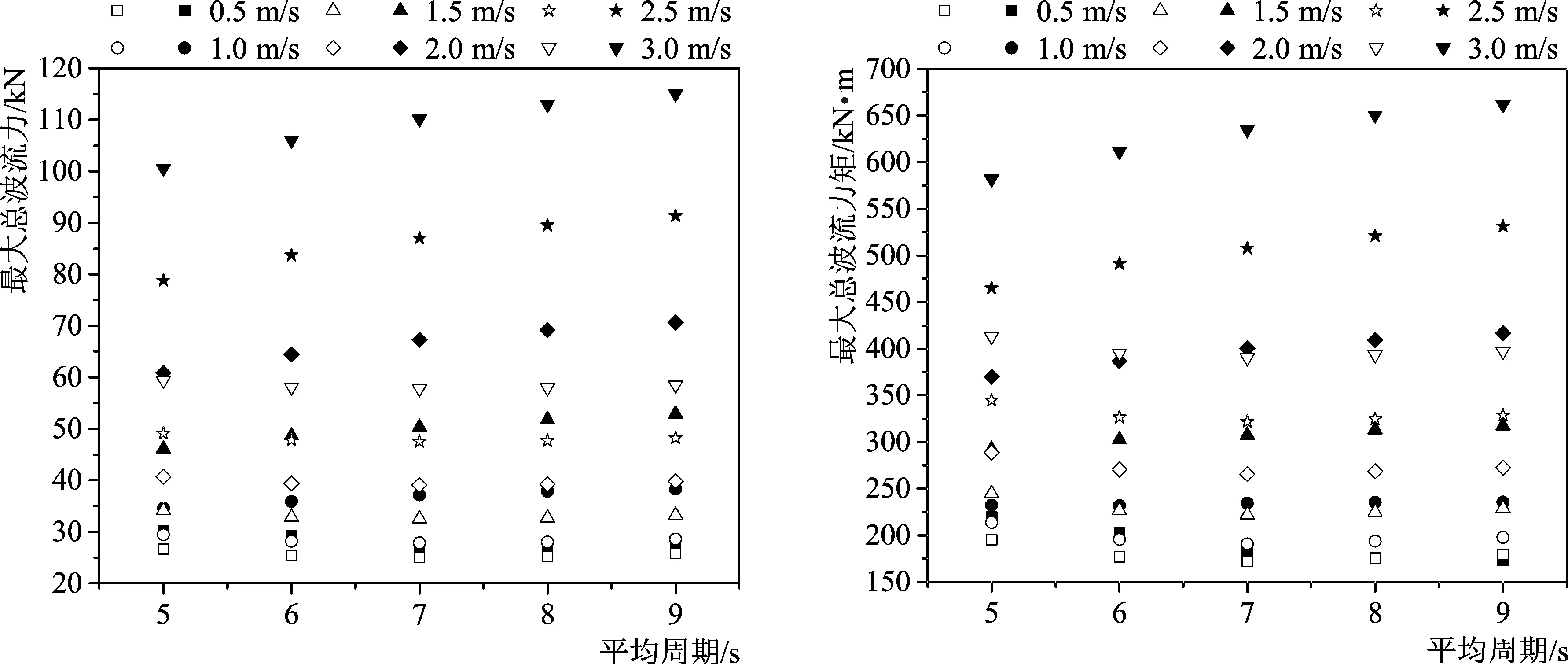
这里首先以3.0 m波高值对应的结果为例，表1和表2分别给出了方法一和方法二的计算结果。为了更加直观地显示，图2和图3分别给出了最大总波流力和最大总波流力矩随流速的变化，结果表明，由方法一和方法二计算得到的最大总波流力和最大总波流力矩均随流速的增大而增大，而且两种方法计算结果的差别也随之逐渐增大，采用方法二得到的最大总波流力和最大总波流力矩分别是采用方法一计算结果的1.05～1.97倍和1.00～1.67倍，说明对于柱桩的工程设计，采用方法二较方法一偏保守。图4和图5则分别给出了最大总波流力和最大总波流力矩随平均周期的变化，方法一计算的两者基本不随平均周期变化，而方法二得到的结果尽管呈现出随平均周期的增大而增大，但增加的幅度逐渐减小，不及其随流速增加的幅度。在以上结论的基础上，这里选取平均周期为9 s时的计算结果，进一步讨论波高的影响效果。图6和图7分别给出了最大总波流力和最大总波流力矩随波高的变化，两者均随波高呈增长趋势。同时，相比于波高和平均周期，流速对两种方法计算结果差异的影响更为显著，随着流速的逐渐增大，其差异也逐渐增大。

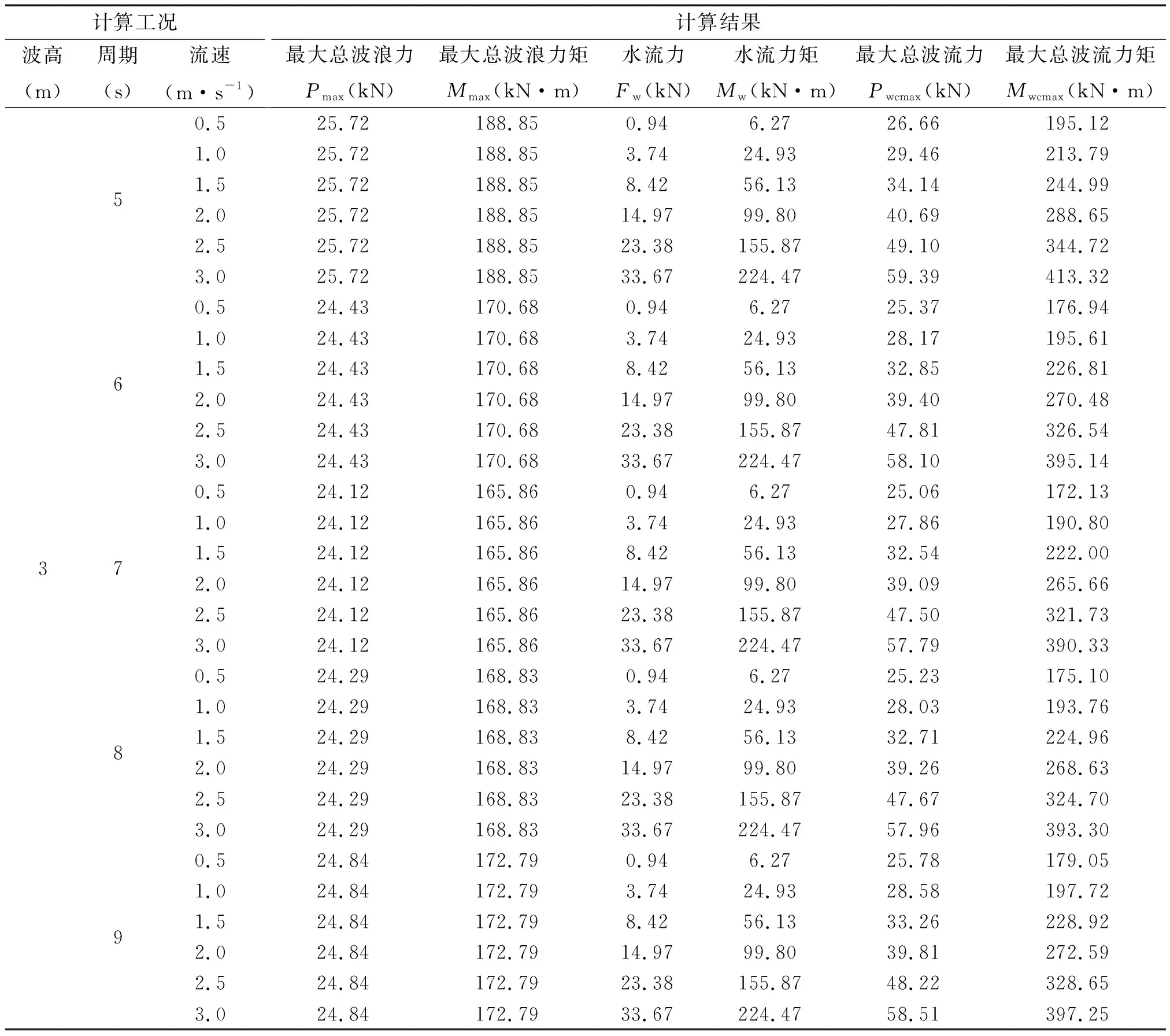
表1 围栏设施柱桩波流力计算(方法一)Tab.1 The wave-current forces on the pile of fence facilities (Method 1)

表2 围栏设施柱桩波流力计算(方法二)Tab.2 The wave-current forces on the pile of fence facilities (Method 2)

注:空心:方法一;实心:方法二。图2 最大总波流力随流速的变化Fig.2 Variation of the maximum total wave-current forces with velocity注:空心:方法一;实心:方法二。图3 最大总波流力矩随流速的变化Fig.3 Variation of the maximum total wave-current torques with velocity

注:空心:方法一;实心:方法二。图4 最大总波流力随平均周期的变化Fig.4 Variation of the maximum total wave-current forces with mean period注:空心:方法一;实心:方法二。图5 最大总波流力矩随平均周期的变化Fig.5 Variation of the maximum total wave-current torques with mean period

注:空心:方法一;实心:方法二。图6 最大总波流力随波高的变化Fig.6 Variation of the maximum total wave-current forces with wave height注:空心:方法一;实心:方法二。图7 最大总波流力矩随波高的变化Fig.7 Variation of the maximum total wave-current torques with wave height

3 结论

本文结合椒江大陈岛海域大型浅海牧场式围栏设施工程设计需求，基于现行规范中常用的两种柱桩波流力的计算方法，对不同波浪和水流条件下最大总波流力和总波流力矩随波高、平均周期和流速的变化趋势进行了探讨，同时比较了两种方法计算结果的差异并分析了影响差异的主要因素，得到如下结论：(1)两种方法得到的最大总波流力和总波流力矩均随波高和流速的增大而增大，而受平均周期的影响较小；(2)方法二的计算结果较方法一偏保守，相比于波高和平均周期，流速对两种方法计算结果差异的影响更为显著，随着流速的逐渐增大，其差异也逐渐增大，现阶段建议在大流速条件下确定围栏设施中柱桩波流力时需结合相应物理模型试验结果。后续将进行浅海牧场式围栏整装设施物理模型试验，对上述两种计算方法进行进一步比较，为浅海牧场式围栏设施中柱桩工程设计和科学研究提供更为有效的参考。