基于灰色预测和ARIMA模型的疾病分析与预测△

魏 杰 张 璇 王 柳 汪丽萍

(安徽蚌埠医学院数理教研室 蚌埠 233030)

颈椎病又称颈椎综合征，是颈椎骨关节炎、增生性颈椎炎、颈神经根综合征、颈椎间盘脱出症的总称，是一种以退行性病理改变为基础的疾患。改革开放以来，随着人民生活水平的提高，颈椎病等慢性疾病越来越受到人们的关注。由有关数据可知颈椎病在各年龄段的分布差异较大，在41～50岁之间出现分布高峰；性别分布有差异，女性患者约为男性患者的两倍；受季节的影响较大，在夏季高发，冬季相对较少。且随着经济和科技的迅猛发展，生活便捷，脑力劳动占据人们的时间日渐增长，身体活动随之减少，颈椎病等退行性疾病威胁着人们的健康。

1 数据来源与模型假设

数据来源：国家中医药管理局十二五重点专科(康复医学科)科研大数据。

模型假设：(1)假设科研大数据所给的数据真实可信，不含有人为修改或虚报的数据；(2)假设数据处理时没有数据的重复和有效数据的丢失，保证数据的单一性和完整性；(3)假设疾病的发生与其他因素无关，不考虑生活和行为习惯的影响。

2 灰色预测模型

2.1 研究思路

针对颈椎病的年发病密度，建立灰色预测模型，预测颈椎病在2014～2016年的发病密度，得出颈椎病发病密度呈逐年增长的趋势。首先把原始数据加工成生成数，得累加生成序列，再次经过紧邻生成得出紧邻生成序列和时间响应序列，用最小二乘法估算发展系数和灰作用量，通过估计值求出预测方程，根据方程得出原始数据的拟合值，进行残差检验、后验差检验和关联度检验，预测方程可靠，从而得出预测值。

2.2 研究方法

现如今，人们的生活水平日渐提高，颈椎病的发病密度有显著变化。本模型是在数据预处理基础上，建立灰色预测模型，运用灰色预测法和 MATLAB 软件编程进行数据分析和处理，推断颈椎病 2014～2016 年的发展趋势。 模型基本流程为：

(1)

及时间响应序列

(2)

其中(-a)为发展系数，b为灰作用量。a和b可通过最小二乘法来估算，方法如下：

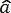
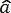
当K≥n时，(2)式为预测方程，其计算结果为预测值。

2.3 结果分析

本题中由数据整理可得2009年～2013年的颈椎病患病人数分别为42,26,78,141,142(由查阅资料可得2014年数据不合理，因此舍去)，因此X(0)=(42 26 78 141 142)。

此时，通过matlab计算(程序见附录)可得原始数据的拟合值为(42，54，78，112，162)，而其预测出的2014～2016年的颈椎病人数分别为234、339、490人。

3 ARIMA模型

3.1 研究思路

针对颈椎病月发病密度，建立自回归积分滑动平均模型(ARIMA 模型)，预测颈椎病的月发病密度，对原始数据进行平稳性检验，不能通过，进行差分处理，使数据能通过平稳性检验后，进行自相关和偏自相关分析和 ARIMA 模型识别，确定p、q值，建立模型。对模型进行残差检验和拟合预测，模型预测可靠。

3.2 研究方法

ARIMA模型是对 ARMA 模型进行优化得来的，属于线性模型，非常适合于预测平稳时间序列。它的基本思想是将预测对象随时间推移而形成的数据序列视为一个随机序列， 用一定的数学模型来近似描述这个序列，这个模型一旦被识别后就可以从过去值及现在值来预测观察值。模型基本流程为：

3.2.1获取数据和预处理

3.2.2ARIMA模型的识别

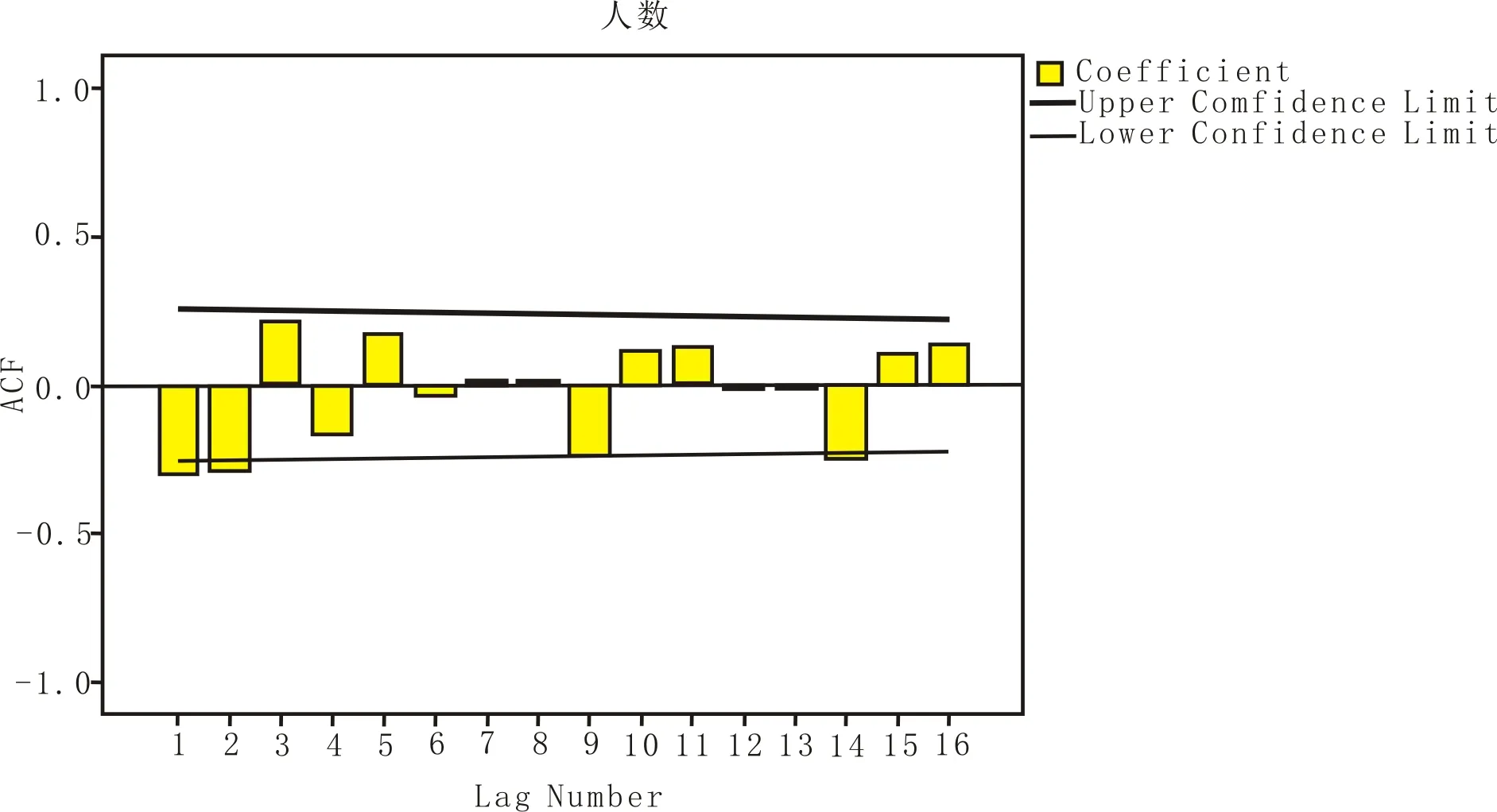
图的自相关函数

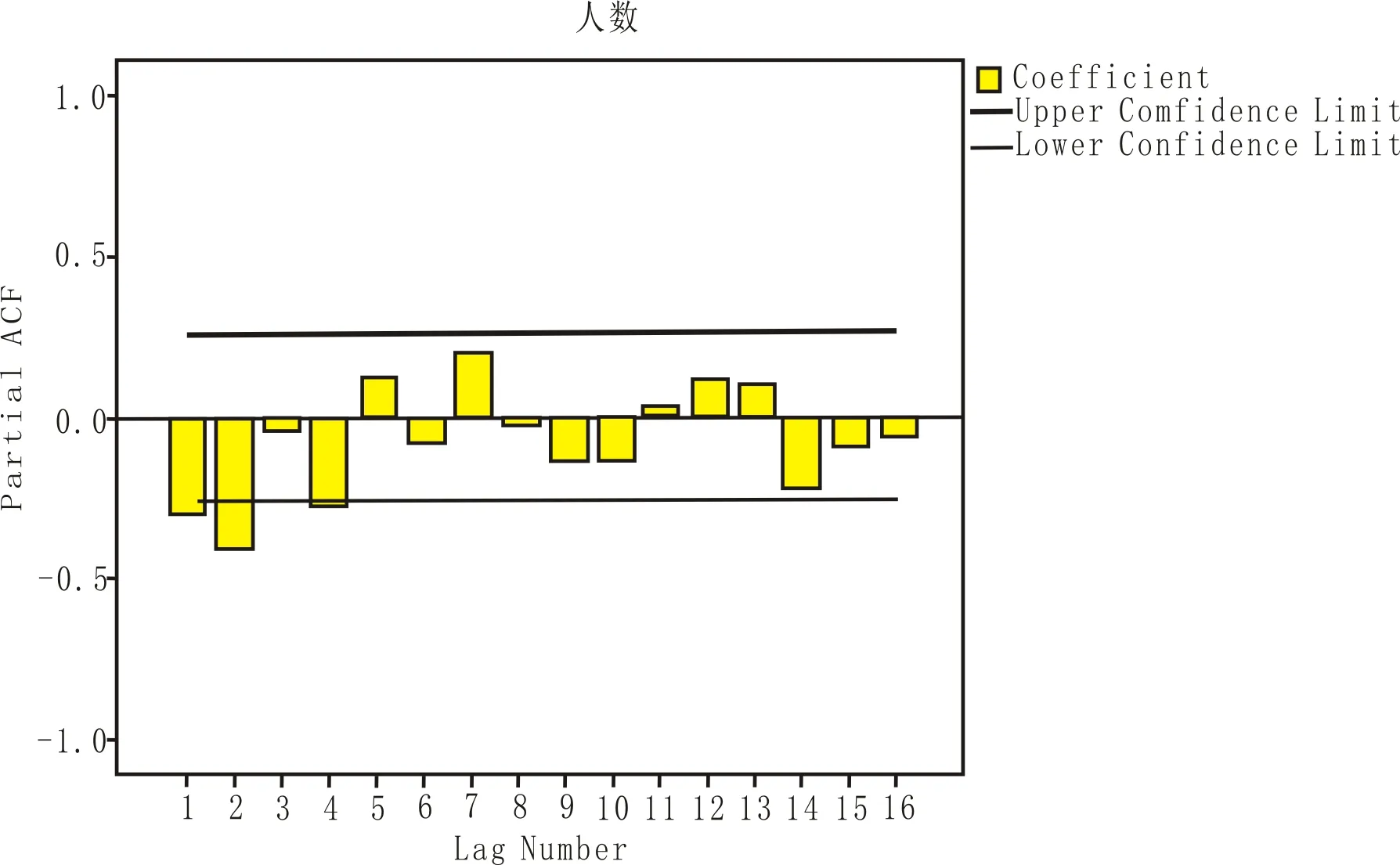
图的偏自相关函数

表1 模型识别原则

模型AR(p)MA(q)ARIMA(p,q)自相关函数拖尾,指数衰减或振荡有限长度,截尾(q 步)拖尾,指数衰减或振荡偏自相关函数有限长度,截尾(q 步) 拖尾,指数衰减或振荡拖尾,指数衰减或振荡

3.2.3参数估计

3.3 结果分析

表2 Model Statistics

ModelNumber of PredictorsModel Fit StatisticsLjung-Box Q(18)Stationary R-squaredR-squaredStatisticsDFSig.Number of Outliers人数-Model_110.3420.64416.24540.0030

R的平方达到0.644，拟合度还好，显著性水平小于0.05，因此系数都显著不为0。

4 灵敏度分析

4.1 灰色预测模型的检验

当K≥n时，(2)式为预测方程，预测方程是否可靠，需对其精度进行检验。本文采用残差检验，关联度检验，后验差检验和小误差概率模型进行检验，其步骤如下：

(1)残差检验:即对模型值和实际值的残差进行逐点检验。

分别计算残差：

相对残差：

(2)后验差检验：即对残差分布的统计特性进行检验。

分别计算：

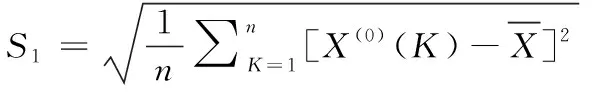
由后验差比值和小误差概率初步推断预测精度等级，见表3。

表3 后验差比值和小误差概率初步推断预测精度等级

预测精度等级PC好>0.95<0.35合格>0.80<0.45勉强>0.70<0.50不合格<=0.70>=0.65

经过matlab计算精度检验可得：

①关联度为61.2585%；

②小概率误差P=1；

③方差比c=0.405581；

④合曲线见图3。

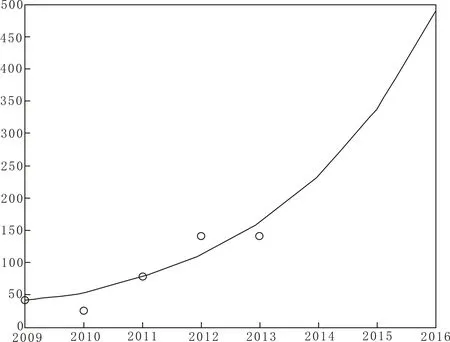
图3 颈椎病MATLAB年份拟合曲线

由此可得此预测合格，该预测具有一定的可靠性。

4.2 ARIMA模型的检验

(1)残差检验

图4 残差的ACF和PACF图

由图4可以看出基本上都是平稳的，因此ARIMA(5,1,9)模型是合理的。

(2)拟合预测

图5 ARIMA(5,1,9)模型拟合效果

由图5可知，观测值都在预测值的置信区间内，拟合效果好。

5 结束语

本文针对颈椎病发病密度在未来几年的发展趋势问题，运用灰色预测模型分析出患有颈椎病的人群在未来几年将逐年增多，运用ARIMA模型进一步分析出患有颈椎病的人群在未来几个月的发展趋势，通过调整ARIMA模型参数使预测结果更加真实可靠，并对两个模型分别用灵敏度分析和残差检验进行判别其预测结果是否可靠。