PGNAA方法测量元素的非线性规律研究
吴志强,龚亚林
(丹东东方测控技术有限公司,辽宁 丹东 118002)
瞬发伽玛中子活化分析(prompt gamma neutron activation analysis, PGNAA)技术使用中子激发物料元素,并对特征伽玛射线进行探测分析,而中子和伽马射线均具有极强的穿透能力,可获取大厚度物料内部全元素信息。因此,PGNAA技术样品测量具有非接触、非破坏性、全元素测量、实时在线分析、可穿透一定厚度的容器及物体进行分析、不受环境影响、分析精度高等特点,普遍用于工业在线检测领域。以水泥生产、煤炭资源、冶金生产等资源消耗密集型产业的使用最具代表性。水泥、冶金行业需要在生产过程中及时掌握物料元素成分信息,以便实现生产过程的节能降耗及产品质量的有效提升;煤炭燃烧过程中,需要了解煤炭的成分信息,以便实现对煤炭使用的高效、环保。PGNAA在线分析仪可及时获取关键工业物料信息,提高生产效率,实现节能降耗,促进落后产能转变。
PGNAA在线分析仪主要有旁线式与跨皮带式,其中跨皮带式安装方便、物料通过性强、维护成本低,市场应用率达到90%以上。跨皮带式PGNAA在线分析仪在投运之前经过实验室静态标定、现场静态标定和现场动态标定。这三个标定程序均基于标准物料厚度,如果厚度发生较大变化,将引起较大的测量偏差。为保证分析仪的测量准确性,通常要求皮带上物料厚度恒定。但由于工业现场的产量变化需求,皮带上物料不恒定,导致产量变化时在线分析仪的测量精度受到较大影响。通常在皮带上加装变频器,当产量变化时,调整皮带的转动频率,保证皮带上物料的厚度不变。但加装变频器会增加采购成本和维护量,且长度超过1 000 m的较长皮带很难实现变频调速,所以工业现场并不希望加装变频器。如何在皮带上物料厚度变化的环境下依然保证在线分析仪测量精度,是亟待解决的问题。为此,本研究结合理论分析和蒙卡模拟研究PGNAA测量不同厚度物料时的误差原因,并寻求厚度修正模型,以适应工业现场产量变化时的元素检测需求。
1 PGNAA原理与蒙特卡罗方法
瞬发伽玛中子活化分析(PGNAA)原理图示于图1。当中子轰击物料时,中子与靶核发生俘获反应,形成复合核。中子被俘获后,原子核处于激发态,随即发射一个或几个瞬发伽玛射线,然后复合核回到基态,或变成放射性核素。瞬发伽玛射线的能量与新形成核的中子结合能有关,所以元素放出特征能量的伽玛射线。以探测瞬发伽玛射线进行元素分析的方法,称为瞬发伽玛中子活化分析[1]。

图1 瞬发伽玛中子活化分析原理图Fig.1 Schematic diagram of prompt gamma neutron activation analysis
蒙特卡罗方法又称随机抽样技巧或统计试验方法,其主要应用范围包括:粒子输运、统计物理、典型数学、真空技术、激光技术以及医学、生物、探矿等方面。蒙特卡罗方法在描述粒子输运时可以应用到实验核物理中,主要包括:计算通量和反应率、中子探测效率、光子探测效率、光子能量沉积谱及响应函数、气体正比计数管反冲质子谱、多次散射与通量衰减修正等。
2 理论分析
PGNAA方法伽玛探测器收集的瞬发特征伽玛射线的强度反映物料中元素含量[2]。当单能平行中子束照射充分薄且均匀样品时,反应率可表达为:
R=nσφ
(1)
式中,R为反应率,s-1;n为中子束照射内原子核数目;σ为给定能量中子俘获截面,cm2;φ为中子通量,cm-2·s-1。考虑探测器的探测效率,特征能量的特征伽玛峰计数率可表达为:
ργ=ε(Eγ)nσγφ
(2)
式中,ργ为计数率,即净峰面积除以测量时间;ε(Eγ)为探测器的探测效率。
但是大部分情况下中子的能量不单一,俘获反应截面与能量相关,被照射样品不可能达到理想的厚度,必须考虑样品内部中子场的变化和伽玛射线的衰减。综合这些因素,得到:
ε′(Eγ,r)dEndr
(3)
式中,μ(r)为样品(不均匀)内部位置r处元素的质量密度;M为元素的相对原子质量;NA为阿伏加德罗常数,6.022×1023mol;σγ(En)为与中子能量相关的特征伽玛射线产生截面;φ′(En,r)是以样品内部位置和能量为变量的中子通量函数(主要为样品内部中子自屏蔽效应);ε′(Eγ,r)是样品内部位置的探测器对特征能量伽玛射线的探测效率(主要为伽玛自衰减效应)。
从公式(3)可以看出,由于物料内部对中子的自屏蔽效应和对伽玛射线的自衰减效应[3-6],被照射物料元素产生的特征伽玛射线强度不可能完全随物料的增多而线性增长。只有物料是理想情况下的足够薄,不考虑物料自身对中子的自屏蔽效应和对伽玛的自衰减效应时,才可以认为特征射线的强度与元素含量或物料厚度成正比。
3 蒙特卡罗模拟
3.1 模拟装置
模拟实验的装置图示于图2。PGNAA装置主要有中子源、慢化体、物料和伽玛探测器等[3]。本研究模拟装置中子源采用252Cf源。选取若干种代表性物料,包括单质:纯净Fe粉,密度为1.4 g/cm3;氧化物:纯净Al2O3、SiO2、CaO,密度分别为3.8、1.5、1.5 g/cm3;混合物料:水泥生料,密度为1.6 g/cm3。

图2 PGNAA模拟装置示意图Fig.2 Schematic diagram of PGNAA analog device
3.2 分析过程
252Cf中子源发射快中子,经慢化体慢化后成为热中子,热中子与物料中的原子核发生俘获反应,放出特征伽玛射线,最后被伽玛探测器接收。
3.3 模拟结果
3.3.1不同厚度单质与氧化物
改变模拟装置的物料种类与厚度,分别模拟计算铝(7.73 MeV)、硅(4.93 MeV)、钙(6.42 MeV)、铁(7.64 MeV)特征射线计数随物料厚度变化的情况。在中子活化元素分析仪的测量装置内分别放入不同厚度的Al2O3、SiO2、CaO、Fe粉,测量中子活化能谱,去除本底,得到特征伽玛射线计数。各元素特征伽玛射线随单质厚度的变化趋势示于图3,实验测量结果与蒙特卡罗模拟结果符合很好。
从图3结果可以看出,铝、硅、钙、铁4种元素物料厚度小于8 cm时,随着厚度增加,特征伽玛射线计数迅速增加;但当物料厚度增加到10 cm时,随着物料厚度的增加,铝、硅、钙的特征伽玛射线计数增长率开始变小,而铁的特征伽玛射线计数随物料厚度的增加下降。这种现象主要由两种效应引起,一是随着物料厚度增加,物料内部的热中子被大量吸收,导致物料内部热中子通量下降,俘获反应的几率相应下降,为中子自屏蔽效应;二是随着物料厚度增加,物料下层产生的特征伽玛射线经过上层物料的衰减后才能到达探测器,降低了特征伽玛射线的探测效率,为伽玛自衰减效应。这两种效应均导致元素特征射线与物料厚度呈现非线性增长规律。模拟中,密度较大的铁粉中子自屏蔽和伽玛自衰减效应均强于密度较小的Al2O3、SiO2、CaO,导致铁特征伽玛射线计数在Fe粉厚度为8 cm时下降。

a——铝(7.73 MeV);b——硅(4.93 MeV);c——钙(6.42 MeV);d——铁(7.64 MeV)图3 元素特征伽玛射线强度与厚度关系a——Aluminum(7.73 MeV);b——Silicon(4.93 MeV);c——Calcium(6.42 MeV);d——Iron(7.64 MeV)Fig.3 Relation between characteristic gamma ray intensity and thickness
3.3.2不同厚度水泥生料
为进一步分析PGNAA方法测量不同厚度物料的特性,分别利用蒙特卡罗模拟和实验测试,研究Al、Si、Ca、Fe元素的特征计数随水泥生料样品厚度变化的规律。由于Al(7.73 MeV)和Fe(7.64 MeV)的特征射线能量值接近,为准确分析,采用能量分辨率较高的高纯锗探测器。水泥生料样品密度为1.6 g/cm3,所含Al2O3、SiO2、CaO、Fe2O3分别为3.2%、12.3%、42.6%、1.9%。模拟与实验结果示于图4。由图4结果可知,水泥生料中Al2O3、SiO2、CaO、Fe2O3的特征射线计数均随物料厚度增长呈现非线性增长规律,厚度小于10 cm时几乎呈线性增加,随后计数增加率变小,在20 cm处伽玛计数趋于饱和。

a——铝(7.73 MeV);b——硅(4.93 Mev);c——钙(6.42 Mev);d——铁(7.64 MeV)图4 元素特征伽玛射线强度与水泥生料厚度关系a——Aluminum(7.73 MeV);b——Silicon(4.93 Mev);c——Calcium(6.42 Mev);d——Iron(7.64 MeV)Fig.4 Relation between characteristic gamma ray intensity and cement raw thickness
4 修正模型
4.1 单质样品
4.1.1Al,Si,Ca
由于PGNAA测量过程中物料内部的中子自屏蔽和伽玛自衰减效应的影响,元素的特征瞬发伽玛射线计数随物料厚度增长呈非线性增长。为此,寻求修正模型,使修正后的射线计数率与物料的厚度变化呈线性增长。首先分析密度较小、质量变化范围较小的Al2O3、SiO2、CaO的修正模型,采用二次多项式进行修正,结果示于图5。
由图5中Al2O3、SiO2、CaO的特征伽玛射线与相对质量(厚度乘以密度)的关系,得到元素Al、Si、Ca的含量修正模型:

图5 元素修正模型Fig.5 The correction model of elements
Y=a*X2+b*X+c
(4)
Al=Al*Y
(5)
Si=Si*Y
(6)
Ca=Ca*Y
(7)
式中,X为特征伽玛计数,Y为修正参数。公式(4)为修正参数计算公式,公式(5)、(6)、(7)分别是Al、Si、Ca的含量修正公式。
4.1.2Fe
Fe粉的含量修正模型示于图6。由于Fe粉密度较大,与Al2O3、SiO2、CaO相比,相同厚度的Fe粉质量较大,物料内部的自屏蔽与自衰减效应较强,导致在物料厚度为8 cm,相对质量为30时,计数率出现拐点,Fe含量无法用通用的修正模型改善测量。因此,当物料厚度和质量变化较小时,可采用多项式修正模型减小自屏蔽与自衰减效应带来的非线性影响;当物料厚度和质量过大时,射线计数出现饱和与下降趋势,无法找到较好的修正模型改善测量精度,只有改善测量条件,如减小被测量物料的厚度或保持物料厚度恒定不变实现测量。
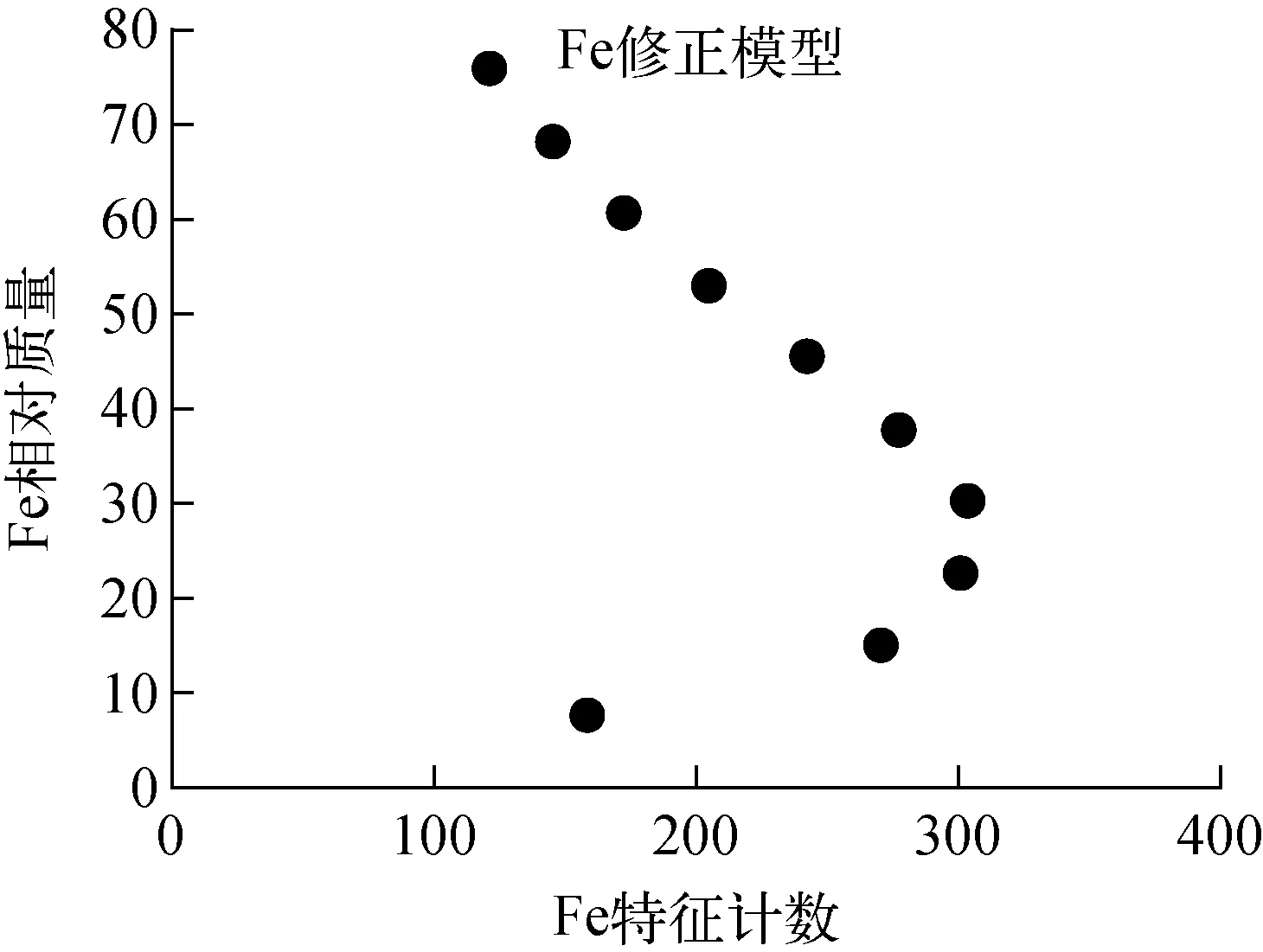
图6 Fe元素修正模型Fig.6 Fe element correction model
4.2 水泥生料
根据对单质样品的计数修正模型的分析与PGNAA测量水泥生料的伽玛计数随厚度变化的非线性规律,考虑采用二次多项式修正模型。水泥生料中Al2O3、SiO2、CaO、Fe2O3的特征计数与相对质量的变化关系及修正模型示于图7。
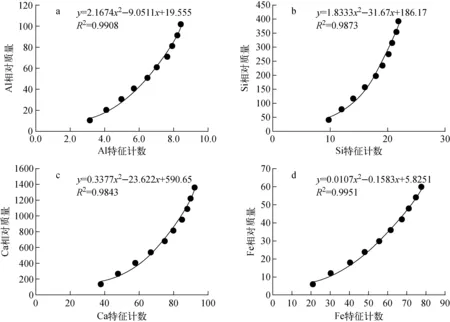
a——Al;b——Si;c——Ca;d——Fe图7 水泥生料元素修正模型a——Al;b——Si;c——Ca;d——FeFig.7 Element correction model for cement raw
如果不考虑各元素的特征射线计数随水泥生料厚度变化的非线性规律,即认为特征伽玛计数随厚度变化完全线性增加,则考虑采用特征伽玛计数与元素相对质量的一元线性拟合,即线性标定。线性标定得到的各元素相对误差示于图8。由图8结果可以看出,不同厚度各元素的相对测量误差较大,多数情况下相对误差超过10%。

图8 线性标定的测量相对误差Fig.8 Measurement relative error of linear calibration

图9 厚度修正后的测量相对误差Fig.9 Measurement relative error after thickness correction
经过多项式厚度模型修正后,水泥生料Al2O3、SiO2、CaO、Fe2O3的测量值与实验值相对误差示于图9。与线性标定的相对测量误差相比,经厚度修正后,各元素的相对误差明显减小,只有个别情况下相对误差超过10%。Al2O3、SiO2、CaO、Fe2O3相对误差的标准偏差分别降低36%、46%、46%、33%。
从修正模型的拟合相关系数看,Al2O3、SiO2、CaO、Fe2O3的拟合相关性较高,达到0.98以上,说明水泥生料的厚度修正模型具有较好的适用性。但修正后各元素的相对误差仍较大,尤其厚度为2 cm时各元素的相对误差达到20%,说明物料厚度过薄(小于2 cm)时,二次多项式厚度修正模型的修正效果较差。当物料厚度较薄时,可以采用分段函数进行修正。但考虑水泥工业现场,皮带上物料的厚度通常集中在10~20 cm,可以忽略物料厚度过小情况下厚度修正模型偏差较大的问题。
5 结论
通过蒙特卡罗模拟与实验测量,利用PGNAA方法测量不同厚度物料时得到以下结论。
(1) 当物料厚度较小时,元素的特征瞬发伽玛射线强度近似随物料厚度的增加而线性增加;当物料厚度较大时,元素的特征瞬发伽玛射线强度随物料厚度的增长率变慢,当物料增加到过厚时,甚至出现下降情况。
(2) 当物料厚度变化范围较小,可以通过多项式修正模型减小自屏蔽与自衰减效应带来的非线性影响。通过多项式厚度修正模型修正后,与线性标定相比,测量相对误差降低30%以上;当物料厚度过大,计数率达到饱和并下降后,修正模型不再适用。需要减小物料厚度或约束物料厚度为恒定值。
通过PGNAA方法测量不同厚度水泥生料的研究,采用修正模型在一定程度上消除了物料厚度变化对测量结果的非线性影响,此修正方法可以推广到透射式跨皮带PGNAA在线分析仪测量煤质、烧结料、铝土矿等块状物料的检测。

