链式回转弹仓的RBF神经网络滑模控制

唐逸雄，陈龙淼，高 波

(1.南京理工大学 机械工程学院，南京 210094； 2.陆军研究院炮兵防空兵研究院，北京 100012)

火炮自动装填系统中，储弹弹仓是非常重要的组成部分。本研究所讨论的链式回转弹仓包含储弹筒、传动链条、传动齿轮、减速器等，其主要完成弹丸的存放、回转选弹工作。如果弹仓的回转定位不够精确，则将会给取弹工作带来困难，甚至发生卡滞，无法取出弹丸，故弹仓的定位精度对其工作效率及可靠性产生较大影响。

弹仓工作过程中，弹丸数量改变导致负载大范围变化，由于弹丸的装弹位置不停变化，等效到电机端的力矩也时刻改变。且弹仓各部分配合由于润滑条件，工作环境变化等外界因素将产生摩擦力矩，振动等非线性扰动。此外，弹仓采用链传动结构，多边形效应和齿轮齿条之间的啮合与冲击也将产生非线性扰动。由此可见，回转弹仓是一种参数不确定的控制对象。针对这类参数不确定控制对象，常用的控制方法有滑模控制，模糊控制，神经网络控制等方法。

滑动模态控制(sliding mode control，SMC)具有快速响应、对参数变化及扰动不灵敏，无需系统在线识别，物理实现简单等优点[2]，因而十分适合机械伺服系统，文献[3]中针对火炮自动装填机械手的位置控制问题，采用了一种自适应动态面滑模控制的算法。通过自适应控制律来估计机械手位置控制过程中不确定性和外加干扰的未知性，抑制了模型的转动惯量等参数变化以及外界干扰的影响。仿真结果表明此方法具有较高的精度和较好的鲁棒性。

模糊控制(Fuzzy Control)，是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种非线性控制技术。采用模糊规则，可根据滑模到达条件对切换增益进行有效估计，并利用切换增益消除干扰项，从而消除抖振[4]。文献[5]中针对链传动机械伺服系统的位置跟踪控制问题，提出了一种采用自适应策略估计系统时变参数的模糊滑模方法，有效减小了模型不确定性的影响，算法对系统参数变化以及外部扰动不敏感，具有较高的控制精度。

径向基函数(radial basis function，RBF)神经网络是非线性系统建模和控制中最常用的网络之一，它模拟了人脑中局部调整、相互覆盖接收域[6]，可以逼近任意精度的连续函数。文献[7]采用一种基于RBF神经网络的滑模变结构控制方法，利用RBF网络逼近动力学方程中难以表示的部分，最终精确控制了船舶航向；文献[8]中针对柔性连杆机械臂关节位置跟踪的奇异摄动技术，设计了一个神经网络控制器，该方法不需要机器人机械臂的先验知识，且不需要离线训练神经网络。

针对链式自动化弹仓精确位置控制时的参数变化、链传动造成的啮合冲击、非线性摩擦等问题，本文受文献[9]中的启发，提出一种基于神经网络最小参数学习法的RBF网络自适应鲁棒滑模控制(adaptive robust sliding mode control for rbf networks，ARSMC-RBF)，通过参数的估计代替神经网络权值的调整，加快了自适应律的求解，并使系统的控制定位达到了较高的精度。

1 动力学模型

本研究所讨论的链式回转弹仓简化结构图如图1所示，工作在力矩控制模式下的永磁无刷直流电机，电机通过减速器等一系列中间机构，带动主动轮转动，从而带动从动轮、储弹筒与弹筒中的弹丸一起转动。电机的电气时间常数远小于机械时间常数，为方便后续工作，忽略电流环动态，不考虑电机内部工作方式，则链式自动化弹仓的动力学方程可以写为

(1)

式中：J为系统等效到电机输出轴的转动惯量；B为系统等效到电机输出轴的黏性阻尼系数；θ为电机转子位移；Td为等效扰动，包括负载力矩、啮合冲击、非线性摩擦力以及其他难以建模的动态等；u为控制输入力矩。

考虑弹仓系统的转动惯量与黏性阻尼系数随弹仓转动及弹丸数量改变而不断地变化，再考虑到由齿轮啮合冲击及多边形效应带来的其他非线性干扰，可以考虑如下2阶非线性系统：

(2)

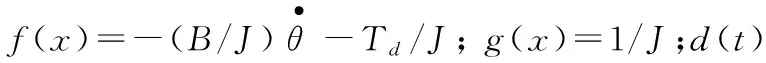
2 控制器设计

设定位置指令为θd，令

e=θ-θd

(3)

设计滑模切换函数为

(4)

式中，c>0。

将式(3)代入式(4)并对s求导可得：

(5)

在实际工程中，模型不确定项f，g为未知，为此，需要对f，g进行逼近。

采用RBF网络对不确定项进行自适应逼近。RBF网络算法为：

(6)

其中：x为网络的输出信号；j为网络隐含层节点的个数；cj和bj分别为基函数的数据中心和宽度，f=[f1，f2，…，fm]T和g=[g1，g2，…，gm]T为高斯基函数的输出；W和V为理想神经网络权值。

(7)

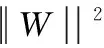
设计控制律为：

(8)

将控制律式(8)代入式(5)，得：

ηsgn(s)+d-μs

(9)

定义李雅普诺夫函数[10-12]：

(10)

其中，γf>0，γg>0。

对L求导，并将式(8)和式(9)代入，得

(11)

(12)

设计自适应律为

(13)

其中，kf>0，kg>0。

将式(13)代入式(12)可得：

(14)

(15)

(16)

(17)

即：

(18)

3 仿真分析与验证

由于链式弹仓弹丸数目较多，故取空载、半载、满载3种情况进行仿真分析。若本算法在上述3种情况下可行，则可以说明本算法适用于链式回转弹仓各状态下的运动控制。

期望轨迹为点到点(Point-to-Point)运动轨迹，如图2所示，最大位移600 rad，最大速度300 rad/s，最大加速度600 rad/s2。期望运动过程为先加速，再匀速，再减速，最后停止，故设定加速度在0.5 s到1 s内为600 rad/s2，在2.5 s到3 s内为-600 rad/s2，其他时间为0。角速度为角加速度积分的结果，同理，角位移为角速度积分的结果。可以看出，期望角位移是一段二阶可导的平滑曲线，可以满足运动过程必须平稳的要求。

RBFSMC的参数设置为：c=15，是滑模面的设计参数；η=1，其作用是克服神经网络的逼近误差，以保证系统稳定，模型经过调试，逼近误差在±1以内跳动，故取1即可； 经过调试，得到各模型参数：μ=30，cj=[-2，-1，0，1，2]，bj=1，自适应参数γf=300，γg=150。在空载且无扰动情况下，仿真结果如图3～图5所示。

由图4和图5可以看出，算法在系统空载且无外界扰动的理想情况下，对期望角速度和期望角位移的跟踪效果良好，角速度误差在10-5rad/s以内，角位移误差在10-4rad以内，由于是空载无扰动的理想情况，故误差的数量级都非常低。接下来将加入扰动，并在空载、半载、满载3种不同情况下进行仿真以验证算法效果。

考虑系统在获得加速度时状态变化较大，等效扰动取如图6不规则函数。在有扰动的情况下，RBFSMC参数不变，算法在弹仓空载、半载、满载的仿真结果如图7～图9所示。

图7为有扰动情况下，系统分别在空载、半载、满载控制输入，对比图3可以看出，在加入外界扰动后及负载变化后，算法的控制输入可以面向扰动及负载变化作出自适应改变。

由图8和图9可以看出，在加入外界扰动及负载变化后，算法对期望位移的跟踪误差始终在±0.1 rad以内。以上仿真结果说明，本文提出的RBF神经网络滑模控制算法对系统参数的大范围变化和外界的不稳定扰动可以进行自适应调整，具有较好的学习性能和较高的控制精度。

4 结论

本文提出一种基于最小参数学习法的RBF神经网络滑模控制方法，利用RBF神经网络万能逼近的特性，逼近控制律中的未知非线性函数，采用神经网络最小参数学习法，通过参数的估计代替神经网络权值的调整，加快了自适应律的求解。空载、半载、满载3种情况下的仿真结果可以看出，本文提出的控制方法不仅对参数大范围变化不敏感，而且对外部扰动的适应性好，可以获得较高的控制精度。