类地坐标系下惯导系统机械编排的合理性分析

朱 琳，李京书，崔 玫

(1.海军潜艇学院，山东 青岛 266000； 2.海军工程大学管理工程系，武汉 430033； 3.中国舰船设计研究中心，武汉 430000)

惯性导航系统是综合机电、光学、数学、控制及计算机等学科的尖端技术，广泛应用于航空航天航海等导航中，特别是在军事领域的潜艇的水下长航，无法接收到外测信息，只能使用自主式导航系统，其重要意义更是不言而喻[1-2]。快速准备(主要取决于惯导系统初始对准的时间)和高精度一直都是考核惯性导航系统性能优劣的两大重要指标[3-5]，改善这两大指标也是该领域广大学者的努力方向。

惯导系统的力学编排方式在文献[6]中给出了指北方位惯性系统、自由方位惯导系统、游移方位惯性系统3种机械编排，这3种编排的共同点，都是将地平坐标系当作导航坐标系，文献[7]比较了几类惯导系统的机械编排方法，提出利用运动学约束改善低精度惯导系统的机械编排精度；在文献[8]中3.5节分别给出了惯性系坐标系机械编排、地球坐标系机械编排、当地地理导航坐标系机械编排以及游动方位导航坐标系机械编排，同时指出远距离导航普遍使用当地地理坐标系机械编排，其原因在于导航数据用北向速度分量和东向速度分量、纬度、经度、和距地球表面的高度来表示，而惯性系和地球系机械编排需要对速度矢量进行转换，并且指出计算机中精确表达地球引力场是非常困难的。因此传统的惯性导航系统通常是将当地地理坐标系(通常是指“原点位于运载体质心，三轴分别指向所在地的东、北、天”，以后用“东-北-天”坐标系)[9-10]作为导航坐标系，其优点是能够比较直观的给出运载体的位置、姿态、速度，但也存在很多问题：

1) 该“东-北-天”坐标系在复杂重力场下运动变化复杂，通常我们认为重力方向是垂直于水平面向下，其反向延长线就认为是天向，北向指向北极。但是当位置更新，纬度的求解是速度分解到“东-北-天”坐标系的北向除以地球半径，这时就默认为天轴反向延长线也就是重力方向过地球质心了，但真实的情况并非如此，下面给出一张更接近于真实地球的仿真图片(图1)，图1的不同颜色是为了区分重力加速度的大小。

从图1可以看出地球是个非常不规则的球体，其重力场分布复杂，多数地方的重力加速度大小、方向均是不同的，由于“东-北-天”坐标系的天向始终与重力方向相反，因此重力场复杂也就说明“东-北-天”坐标系指向复杂，参考秦永元编写的国家级规范教材对“东-北-天”坐标系的定义：原点位于运载体质心，三轴分别指向所在地的东、北、天。对于该坐标系认定问题，大体有两种认识：一种是从工程实际出发，测站的铅垂线所指的反方向，也就是“东-北-天”坐标系中的“天向”被认为是“工程”重力的反向延长线，“东-北-天”坐标系跟踪的是大地水准面；另一种认为“东-北-天”坐标系是属于地理概念，是为了更好的描述位置，确定地理经纬度，假想一个参考椭球面，通常以参考椭球面的法线作为理论“东-北-天”坐标系的天轴方向，以确定地理纬度，但这个理论的天轴在工程上很难获取，现常用的参考旋转椭球体就有五个，分别是克拉索夫斯基、海福德、1875年国际推荐、克拉克、CGCS2000，旋转椭球体与大地水准体非常接近，在垂直方向最大误差约为150 m，垂线偏离真垂线最大误差，如果这一误差不被允许，如何确定该地理垂线的方向是工程实践的一大难题。

2) 陀螺直接测量的是从惯性系到载体系的旋转角速度，以“东-北-天”坐标系为导航系，姿态更新过程需要扣除地球自转角速度和地球系“东-北-天”坐标系的旋转角速度，动基座下该旋转角速度不为0，需要寻求方法对其进行补偿，但复杂机动过程，补偿效果常常不令人满意。

3) 在极区导航时，以“东-北-天”坐标系的机械编排并不适用，因为对于平台式惯性导航系统，在这种机械编排下的导航系y轴要始终指向真北，当水下潜器通过极点附近时，真北很快变化，此时导航系y轴指向变化的速率将会无穷大。对于捷联式惯导系统，则在极点处存在计算溢出的问题，以往的方法是采用游动方位坐标系来解决这一问题，但该方法无法在极区指示方向，针对这一问题，将坐标系旋转90°的横坐标系成为极区导航的研究热点，但航行到纬度多少的时候切换到横坐标系下导航并没有明确。

基于以上传统的惯导系统选取“东-北-天”坐标系作为导航坐标系存在的问题，考虑定义一种更加合理的坐标系作为导航坐标系是非常必要的，本文详细分析了适合作为导航坐标系的必要条件，定义了一种新的坐标系作为导航坐标系，在新的导航坐标系下，姿态更新精度将会大大提高，从原理上更适用于进行动基座对准、极区导航等任务。

1 新导航坐标系的合理性

导航坐标系作为惯性导航系统直接用来定位、定姿、定速的坐标系，直接影响到导航精度，其重要性毋庸置疑，导航坐标系选取不合理就会从根源上引入误差，使得系统无论怎么补偿改进都不会令人满意，在这里首先深入分析导航坐标系在选取上需要把握的几个原则，然后定义一个新的坐标系作为导航坐标系。最后，建立新的惯导系统机械编排、姿态、速度、位置更新方程。

为了便于分析和讨论，首先定义几个坐标系，图2中椭球代表地球，坐标系表示如下：

地心惯性坐标系i：原点位于地心，xi轴指向春分点，zi轴沿地球自转轴，yi轴与xi、zi轴构成右手系。

地球坐标系e：原点位于地心，xe轴穿越本初子午线与赤道的交点，ze轴穿越地球北极点，ye轴穿越东经90°子午线与赤道的交点。该坐标系与地球固联，见图2中O-xeyeze坐标系。

“东-北-天”坐标系t：原点位于运载体质心，xt，yt，zt分别指向所在地的东、北、天，见图2，O-xtytzt坐标系，其中重力g方向与zt方向相反。

载体坐标系b：原点位于载体质心，xb，yb，zb分别指向右、前、上。

由于“东-北-天”坐标系存在的前文提到的诸多问题，所选取的新坐标系作为导航坐标系，需要满足以下条件：

① 该坐标系要以载体质心为原点，以便于进行航迹推算。

② 该坐标系尽可能严格，避免进行大量近似。

③ 作为基准坐标系，需要能够确定。

基于以上原则考虑选取类地坐标系n作为新的导航坐标系，类地坐标系定义如图2中O-xnynzn坐标系所示：以载体P为原点，zn是指向地球自转轴的方向，xn在由地球自转轴和重力加速度g所在平面上，与zn垂直指向外，yn轴方向由右手定则确定指向。

值得注意的是：载体和地球的万有引力G是指向地心的，而载体的向心加速度ac是指向自转轴的，而自转轴是通过质心的，则g=G-ac，且3个矢量都在载体与自转轴所确定的平面内，也就是说任意位置的重力加速度矢量都在该位置与自转轴所确定的平面内，静基座条件下，自转轴可由陀螺输出确定指向，而重力加速度可由加速度计确定指向，即可确定O-xnynzn坐标系的三轴指向。动态过程通过姿态方程和导航方程进行姿态和位置的更新，不需要实时确定坐标系指向。

为了便于位置更新，定义切向坐标系R系：以载体P为原点，zR在OP延长线上指向外，xR在以O位圆心、OP为半径的圆上P点的切线方向指向自转轴，yR轴方向由右手定则确定指向。

需要强调的是：如图2所示，对于不规则的地球，重力不指向地心，因此传统的惯导系统将速度分解在yt方向的分量除以地球短轴半径来表示纬度的变化率，这是不严格的，准确的表达应该是载体速度在以O为圆心，以OP为半径做一个圆，在这个圆上P点处的切线方向的速度分量除以OP来表示纬度变化率(由于对椭球曲率的测量问题，不同国家采用不同的参考旋转椭球体，对同一点的纬度标绘也不一致)。

则可以看出类地坐标系具有以下特征：

① 类地坐标系以载体质心为原点，便于航迹推算。

② 类地坐标系n系是由地球坐标系e系通过旋转自转轴得到的，旋转的角度只和P点当地的经度有关，只绕一个轴旋转，属于基本旋转方式。避免了像“东-北-天”坐标系一样需要进行复杂的坐标系变换，况且旋转次序影响旋转效果，需要小角度近似，这样在极区角度变化很大的时候，也能够保证导航和定姿精度。

③z轴方向就是自转轴的方向，通过静止时陀螺组件输出的矢量，其指向即可确定，重力加速度计矢量g可由加速度计输出确定，则根据定义三轴指向可知，基准坐标系可以确定。

⑤ 由于引入了切向坐标系R系，使得经纬度的更新更加严格，从原理上对地球本身的形状没有要求。

⑥ 对于静基座下，“东-北-天”坐标系也是确定不变的，通过对g矢量的解析即可确定，因此，从原理上，静基座下，无论是以“东-北-天”坐标系还是以类地坐标系作为导航坐标系，其导航精度相当，一旦运动起来，“东-北-天”坐标系需要进行复杂的坐标系转换，本文所提机械编排才会展示其优越的性能。

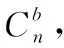
“东-北-天”坐标系的优点在于能够比较直观的给出符合人们习惯的运载体的位置、姿态、速度，其实这一环节完全可以在后期的位置姿态描述中进行投影，不需要参与到导航方程中的迭代解算(避免“东-北-天”坐标系产生的误差引入迭代运算)。如图2所示，导航解算过程不需要经过“东-北-天”坐标系，“东-北-天”坐标系仅仅作为导航信息表述坐标系。

2 新的惯性导航系统机械编排与传统编排方法的性能分析

为了说明类地坐标系作为导航坐标系的优势，将两种方法进行比较。

首先给出传统的“东-北-天”坐标系下惯导系统的基本方程：

姿态方程：

(1)

速度方程：

(2)

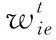
位置方程：

(3)

下面选用类地坐标系作为导航坐标系，直接给出新的导航基本方程：

姿态方程：

(4)

速度方程：

(5)

位置方程：

(6)

(7)

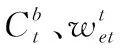
(8)

关于位置方程的更新，由图2，显然式(6)比式(3)准确。

那么可得结论，此机械编排比传统以“东-北-天”坐标系为导航坐标系的编排更为准确。

3 可行性仿真验证

为了说明算法的有效性和合理性，这里通过轨迹生成器模拟陀螺和加速度计的输出，给出不同机动状态下的输出运动轨迹以便于误差比较。由于实验条件限制，静基座实验理论上和传统的编排方法没有任何优势，这一点在文中第二节⑥进行了阐述，而运动起来，又不易找到理想的比对信息，因此这里只给出仿真实验验证算法的有效性。

载体的仿真航行时间为900 s，起始位置是[纬度，经度，高度]=[34°，108°，380 m]，初始航行状态是静止，这里使载体进行加速、左转弯、右转弯、抬头、低头、减速等不同机动，以充分验证该编排算法的有效性和合理性，具体运动状态参数如表1所示。

各仿真参数为：三个陀螺的常值漂移均为0.01 (°)/h，随机漂移均为0.001 (°)/h；三个角速度计的常值零偏均为10-5g，随机误差均为10-5g；初始对准以后的初始水平姿态(俯仰、横滚)误差角30″，初始方位误差角3′；初始速度误差(0.01 m/s，0.01 m/s，0.01 m/s)。

该试验通过已知的运动信息及地球信息，模拟出混入常值和随机误差的陀螺和加速度计的输出，然后利用本文所提的机械编排方法解算出速度信息，姿态信息及位置信息，并和已知运动轨迹进行比较。

表1 运动状态参数

图4给出了整个运动过程的速度解算效果，分别给出了仿真轨迹真值V0，通过本文所提的新的机械编排方法借助陀螺加速度计输出解算出来的轨迹V，以及解算的速度误差(以上两者做差)δV；图5给出了整个运动过程的姿态解算效果，分别给出了仿真姿态真值φ0，通过本文所提的新的机械编排方法借助陀螺加速度计输出解算出来的载体姿态φ，以及解算的姿态误差(以上两者做差)δφ；图6给出了整个运动过程的位置解算效果，分别给出了仿真位置真值P0，通过本文所提的新的机械编排方法借助陀螺加速度计输出解算出来的位置P，以及解算的位置误差(以上两者做差)δP。

4 结论

新构建的机械编排方法中，导航解算是在类地坐标系下完成的，姿态的更新精度更高，将类地坐标系投影到“东-北-天”坐标系下，符合人们的直观表述，有利于在一个坐标系下改善“东-北-天”坐标系下极区导航问题。