三体追逃攻防博弈分析与新型拦截制导律研究
丁一波,毛 伟,王小刚, 崔乃刚
(1. 哈尔滨工业大学航天学院,哈尔滨 150001;2. 试验物理与计算数学国家重点实验室,北京 100076)
0 引言
为了应对日趋完善的导弹防御系统,进攻弹头在发射的同时会伴随一枚防卫弹头,对来袭拦截弹进行主动拦截,掩护弹头突防。这对导弹拦截提出了巨大挑战。因此,近年来,设计三体飞行器的追踪-逃逸场景备受关注,为了应对这种场景,为拦截弹设计一种可行的新型制导律迫在眉睫。三体攻防博弈场景主要涉及3个对象飞行器:进攻弹、防卫弹和拦截弹,如图1所示。

图1 三体攻防博弈作战场景示意图Fig.1 Engagement scenario of conflict for three players
李博文[1]以一对一拦截制导问题为背景,将博弈末制导问题转化为博弈论中的二人竞争博弈模型。Horie等[2]利用数值方法和带有非线性规划的半主动分配方法求解一对一追逃博弈问题。孙传鹏[3]利用模型预测控制的思想,求解一对一拦截问题动态博弈模型的均衡解。Talebi等[4]研究了多枚拦截弹与一枚进攻弹博弈对抗的作战场景,并分析了3种不同的拦截博弈策略:第1种考虑多枚拦截弹协同编队实施拦截;第2种考虑多枚拦截弹不合作单独拦截;第3种考虑多枚拦截弹各自独立作战,并且互相竞争拦截。韩冰[5]、Sun等[6]考虑多弹协同问题,进攻弹与防卫弹相互协作与拦截弹实施博弈,辅助进攻弹突防,提升进攻弹生存能力。Qi等[7]通过全面分析三体攻防博弈中的多种作战情况与作战策略,划分拦截弹可拦截区域,并以此为依据,为进攻弹设计有效的突防制导律。Liu等[8]针对拦截弹提出一种基于模糊评估与纳什均衡的分布式在线任务规划算法。Sun等[9]考虑了四体问题,即一枚进攻弹、一枚拦截弹与两枚防卫弹的攻防作战博弈问题。通过设计两枚防卫弹相互协作,高效辅助进攻弹实施突防。
本文以三体攻防博弈对抗为研究对象,针对不同的攻防对抗初始作战条件进行分析,并为拦截弹提出新型制导律,实现对防卫弹的躲避以及对进攻弹的成功拦截。
1 动力学模型构建
三体攻防博弈任务图如图2所示。在三体攻防博弈下,进攻弹(T)的作战任务是规避拦截弹;防卫弹(D)的任务是追击拦截弹,掩护进攻弹突防;拦截弹(A)的任务是躲避防卫弹,追踪进攻弹,成功实施拦截。作战平面如图3所示。

图2 三体攻防博弈任务图Fig.2 Task of conflict for three players

图3 作战平面Fig.3 Engagement plane
其中,VA、VD和VT分别为拦截弹、防卫弹和进攻弹的速度。γA、γD和γT分别为拦截弹、防卫弹和进攻弹的飞行路径角。λAT为AT之间视线角,λAD为AD之间视线角。RAT为AT之间相对距离,RAD为AD之间相对距离。aA、aT和aD分别为拦截弹、进攻弹和防卫弹的机动加速度。
动力学方程如下:
(1)
(2)
(3)
(4)
将碰撞三角形附近的飞行运动在LOS0周围线性化,下标0表示初始状态。A与T之间垂直于LOSAT0的位移表示为yAT,A与D之间垂直于LOSAD0的位移表示为yAD。
定义A垂直于视线AT的加速度为uA,T垂直于视线AT的加速度为uT,D垂直于视线AD的加速度为uD。其满足如下条件
(5)
选择如下状态变量
(6)
状态方程给出如下[10]:
(7)
状态方程整合如下:
(8)
其中,
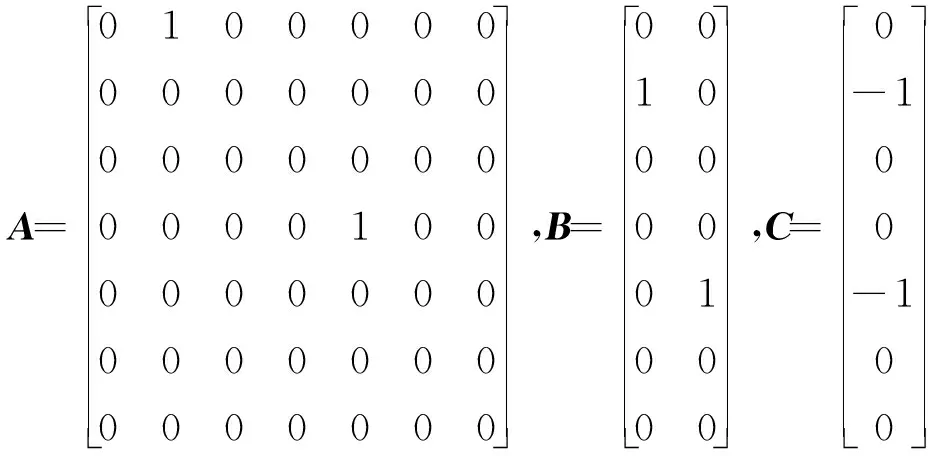
2 微分对策制导律
2.1 变量定义
(9)
式中,下标0表示作战初始状态。由于防卫弹的作战任务是掩护进攻弹,所以要求AD之间作战时间必须小于AT作战时间。即
(10)
定义零控脱靶量为导弹与目标在无控状态下,在预测命中时刻相对于当前视线方向的侧向位移,符号ZAT(t)与ZAD(t)分别表示AT、AD之间的零控脱靶量。
(11)
其满足如下动力学方程:
(12)
式中ZAT与yAT的正负符号定义如图4所示。
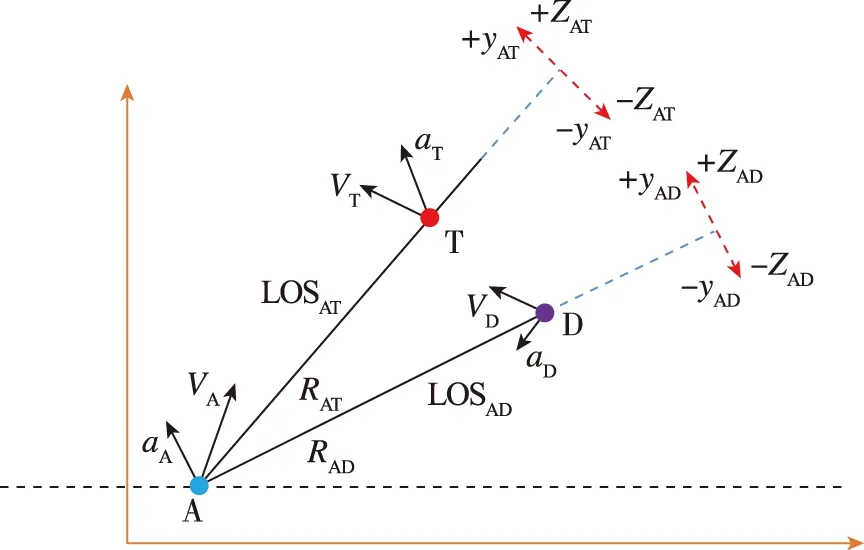
图4 ZAT与yAT 的正负符号定义Fig.4 Definitions of signs for ZAT and yAT
2.2 最优制导律求解
选定如下性能指标:
(13)
求解最优问题可以得到拦截弹与防卫弹之间作战的最优制导律如下[11]:
(14)
拦截弹与进攻弹之间作战的最优制导律如下:
(15)
3 拦截弹新型制导律研究
3.1 AD作战拦截弹最优机动躲避区域
(16)

ZAD(t)=ZAD(t=0)+
(17)
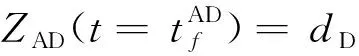
(18)
假定在AD作战中,A与D均应用式(14)的最优机动策略,则若ZAD位于两条边界围成的区域内,拦截弹将会被防卫弹拦截;若ZAD位于两条边界围成的区域外,拦截弹可以成功躲避防卫弹。
3.2 AT作战拦截弹最优机动追踪区域

(19)

ZAT(t)=ZAT(t=0)+
(20)

(21)
假定在AT作战中,A与T均应用式(15)的最优机动策略,则若ZAT位于两条边界围成的区域内,拦截弹可以成功拦截进攻弹;若ZAT位于两条边界围成的区域外,拦截弹无法拦截进攻弹。
求解可得对于拦截弹,实现成功拦截的初始最大允许脱靶量如下:
(22)
下面将三体攻防对抗作战场景划分为2种情况:ZAT(t=0)与ZAD(t=0)的符号相反,ZAT(t=0)与ZAD(t=0)的符号相同。其中第2种情况分为3种条件:1)ZAD(t=0)属于较大正数;2)ZAD(t=0)属于较小正数; 3)ZAD(t=0)不满足条件1)与条件2)。(本文仅讨论ZAD(t=0)为正数的情况,对于ZAD(t=0)为负数的情况,结论与正数情况下相对称,因此不再赘述。)
3.3 情况1
第1种情况下,ZAT(t=0)与ZAD(t=0)的符号相反,分析制导律式(14)与式(15),此种情况下,拦截弹实现最优躲避与最优追踪的控制方向相同。因此,拦截弹可以在对进攻弹执行最优追踪的同时,实现对于防卫弹的最优躲避。图5给出情况1下的零控脱靶量初始条件。

图 5 情况1下零控脱靶量初始条件Fig.5 Initial condition of ZEM(Zero-effort-miss) for case 1
3.4 情况2
第2种情况下,ZAT(t=0)与ZAD(t=0)的符号相同,分析制导律式(14)与式(15),此种情况下,拦截弹实现最优躲避与最优追踪的控制方向相反。因此,拦截弹相对于进攻弹执行最优追踪的同时,相对于防卫弹执行的则是最坏躲避。图6给出情况2下的零控脱靶量初始条件。

图6 情况2下零控脱靶量初始条件Fig.6 Initial condition of ZEM for case 2
本小节对这种情况下AD作战结果进行研究,分析拦截弹成功躲避防卫弹的所需条件。下面将所需条件分3类进行讨论。
(1)条件1
在第1种条件下,ZAD(t=0)属于较大正数。图7给出第1种条件下的零控脱靶量初始条件。
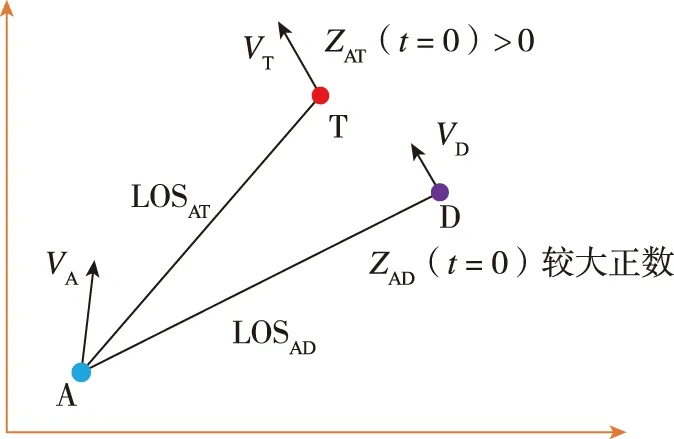
图7 条件1下零控脱靶量初始条件Fig.7 Initial condition of ZEM for condition 1

(23)
求解可得:
ZAD(t=0)≥dD+
(24)
结合式(22)与式(24)可以得到保证拦截弹赢得三体攻防博弈的ZAD(t=0)与ZAT(t=0)初始条件:
(25)
(2)条件2
在第2种条件下,ZAD(t=0)属于较小正数。图8给出第2种条件下的零控脱靶量初始条件。

图8 条件2下零控脱靶量初始条件Fig.8 Initial condition of ZEM for condition 2
同样类比条件1,可得到如下方程:
(26)


(27)
结合式(22)与式(27)可以得到保证拦截弹完成三体攻防博弈的ZAD(t=0)与ZAT(t=0)的初始条件:
(28)
(3)条件3
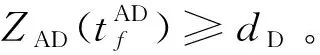
(29)

(30)
在这种条件下,若ZAT(t=0)满足式(30),则应用本文提出的新型制导律可以保证拦截弹在成功躲避防卫弹的同时命中进攻弹,赢得三体攻防博弈对抗。
结合式(15)与式(29)可得最终的拦截弹制导律:
(31)
其中:
(32)
(33)
4 仿真
本小节中,应用实际攻防对抗场景验证所提出的制导律的有效性,其中大气层外拦截器(A)拦截进攻弹头(T),小型智能拦截器(D)作为防卫弹攻击大气层外拦截器,保护进攻弹头。防卫弹与拦截器的杀伤半径dD与dA分别设定为2m与1m。
仿真作战场景如图9所示,表1~表2分别给出大气层外拦截器的性能参数与仿真初始参数。

图9 仿真作战场景Fig.9 Simulation scenario

参数名称参数数值初始质量/kg35燃料质量/kg10轨控发动机推力/N3400

表2 初始参数
4.1 情况1仿真
表3给出情况1下的初始仿真参数。

表3 情况1初始参数
初始脱靶量值ZAT(t=0)和ZAD(t=0)分别为-1526m和364.6m,符号相反。拦截弹仅相对于进攻弹采用最优追踪制导律即可命中进攻弹同时躲避防卫弹。
图10给出的是3个飞行器的攻防博弈飞行轨迹。其中AT作战脱靶量为0.044226m,AD作战脱靶量为1093.4345m。仿真表明,拦截弹可以成功躲避防卫弹并成功拦截进攻弹,赢得三体攻防博弈。

图10 情况1的飞行轨迹Fig.10 Fight path of case 1
4.2 情况2仿真
ZAT(t=0)和ZAD(t=0)符号相同。
(1)条件1
表4给出情况2条件1下的初始仿真参数。

表4 例1初始参数
对应条件1,ZAD(t=0)属于较大正数。初始脱靶量值ZAT(t=0)和ZAD(t=0)分别为-1526m和-1725m,符号相同。
图11显示AT作战脱靶量为0.044226m,AD作战脱靶量为498.2268m。因此,拦截弹可以成功躲避防卫弹并成功拦截进攻弹,赢得三体攻防博弈。
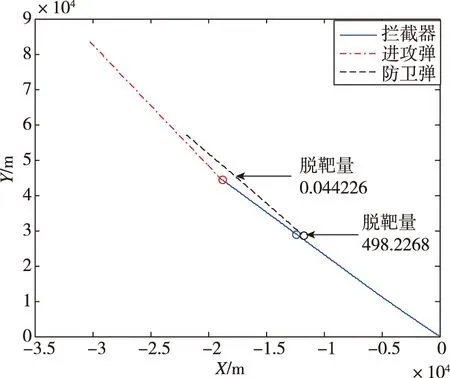
图11 条件1的飞行轨迹Fig.11 Fight path of condition 1
(2)条件2
表5给出情况2条件2下的初始仿真参数。
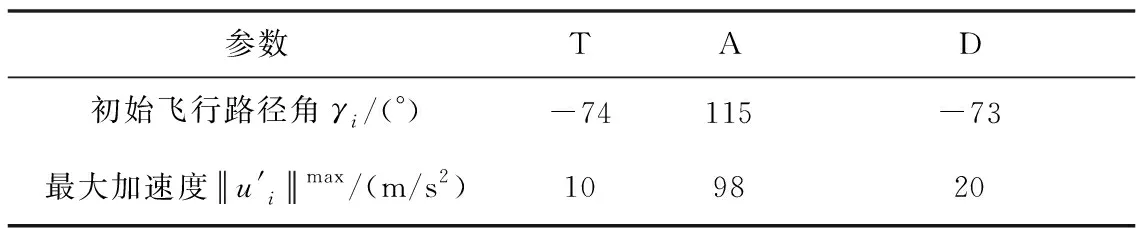
表5 例2初始参数
对应条件2,ZAD(t=0)属于较小正数。初始脱靶量值ZAT(t=0)和ZAD(t=0)分别为-1526m和-157.6m,符号相同。
图12显示AT作战脱靶量为0.044226m,AD作战脱靶量为624.0914m。因此,拦截弹可以成功躲避防卫弹并成功拦截进攻弹,赢得三体攻防博弈。
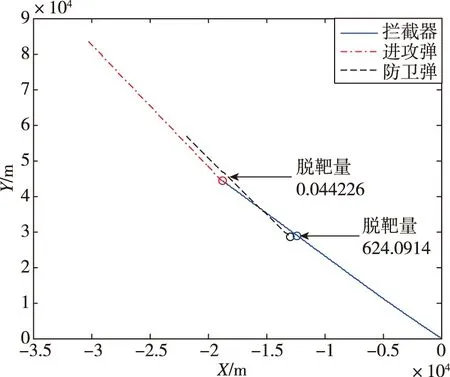
图12 例2的飞行轨迹Fig.12 Fight path of condition 2
(3)条件3
表6给出了情况2条件3下的初始仿真参数。

表6 例3初始参数
对应条件3,ZAD(t=0)不满足条件1与条件2。在这一条件下,执行2组仿真。第1组仿真中,拦截弹仅应用一对一最优制导律追踪进攻弹。第2组仿真中拦截弹使用本文提出的新型制导律。
图13给出的是第1组仿真结果。该组仿真情况下,AT作战脱靶量为0.016644m,但AD作战脱靶量为0.31179m。表明尽管拦截弹可以依据最优制导律成功拦截进攻弹,但是却无法成功躲避防卫弹,拦截弹博弈失败。
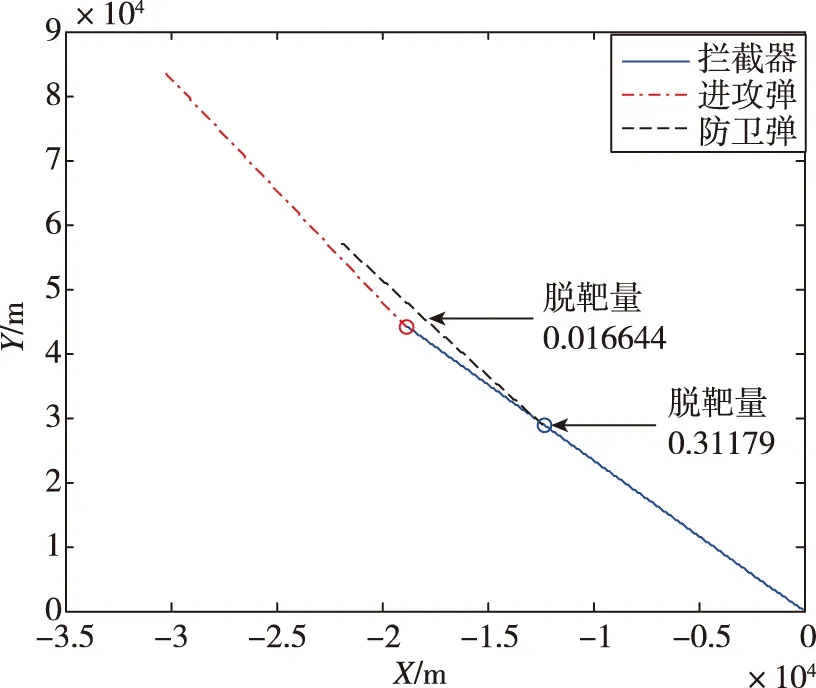
图13 例3第1组仿真的飞行轨迹Fig.13 Fight path for the first simulation of example 3
图14给出的是应用本文制导律的第2组仿真结果。该组仿真情况下,AT作战脱靶量为0.22464m,AD作战脱靶量为327.0642m。表明应用本文制导律,拦截弹可以成功躲避防卫弹,然后精确命中进攻弹,完成预定任务。

图14 例3第2组仿真的飞行轨迹Fig.14 Fight path for the second simulation of example 3
5 结论
本文针对三体攻防博弈问题,基于微分对策理论,研究分析了拦截弹赢得博弈的不同情况,并为拦截弹提出一种新型制导律。在ZAT(t=0)和ZAD(t=0)符号相反时,拦截弹仅使用最优一对一制导律追踪进攻弹,即可同时躲避防卫弹并命中进攻弹。在ZAT(t=0)和ZAD(t=0)符号相同时,分3种条件讨论。前2种条件下,拦截弹同样仅应用最优一对一制导律追踪进攻弹即可赢得三体博弈。对于第3种条件,本文提出一种新型制导律,使得拦截弹可在AD作战时间内有效躲避防卫弹,并保证与进攻弹之间零控脱靶量最小,在AD作战结束后,拦截弹对进攻弹实施最优追踪,赢得三方博弈。

