基于RBF神经网络的导弹智能控制系统设计
徐世昊,崔乃刚,韦常柱
(哈尔滨工业大学航天学院,哈尔滨 150001)
0 引言
面对21世纪复杂多变、对抗激烈的战场环境,世界各军事大国均积极发展以人工智能技术为核心的新一代智能导弹武器系统[1]。而智能导弹武器系统的发展,离不开智能控制技术在导弹上的应用。
智能控制技术于1971年首次被提出之后,由于其强大的学习能力和对外界环境的适应能力,迅速成为控制领域的前沿研究方向。目前理论发展较完善,且取得广泛应用的智能控制方法主要有模糊控制、神经网络控制、专家控制和自适应控制、自组织控制和迭代学习控制等[2]。国内外许多学者将智能控制技术运用到导弹控制系统设计中,取得了丰富的研究成果。其中,崔乃刚等[3]为解决不确定海况对潜射导弹出水姿态的影响,设计了潜射导弹模糊PID分段控制器。王强等[4]利用径向基函数网络与K-means最邻近聚类算法对导弹逆动力学系统进行动态模型辨识,实现了三通道解耦控制。Rong等[5]为倾斜转弯导弹设计了自学习模糊控制器,通过扩展序贯自适应模糊推理系统与传统Back-Stepping控制方法的结合,提高了控制系统应对气动偏差和外界干扰的能力。Ran等[6]在导弹制导控制一体化系统中加入自适应模糊系统以逼近系统不确定性,并推导了保证系统稳定性的模糊系统参数自适应调节律。Lee等[7]基于状态依赖Riccati方程与模块化神经网络设计了导弹助推段的自动驾驶仪。王枫等[8]采用拟人控制方法,基于广义归约的方法将导弹姿态控制问题分解成若干本原问题,之后根据各本原问题的主次关系及耦合关系设计非线性控制律,最后利用遗传算法优化控制器中相应权值。其他学者的研究也主要集中在将智能控制与传统控制方法相结合,以提高导弹控制系统面对诸如舵控效率不足[9]、多执行机构复合控制[10]、气动偏差[11]、模型不确定性[12]等情况下的控制能力,而此类方法的性能往往受限于传统控制方法,且没有利用大量数据对神经网络进行离线训练,以充分发挥神经网络的强大学习能力。
本文利用神经网络强大的逼近能力和学习能力,俯仰/偏航通道采用飞行数据离线训练神经网络的方式,训练完成的神经网络可以直接用作控制器;滚转通道采用神经网络在线调整权值的方式以对系统误差实时逼近;并将两种控制器同时应用于某型倾斜转弯导弹非线性六自由度仿真中,验证了所设计控制器的有效性。
1 导弹控制模型建立及神经网络训练样本获取
1.1 控制模型建立
神经网络的离线训练需要大量样本的支撑,而样本的获取又依赖于传统控制器产生的大量仿真数据。本文设计符合性能要求的PID控制器,然后通过仿真获得足够的神经网络训练样本。
将导弹运动方程组进行小扰动线性化处理,忽略由于重力影响等所产生的动力系数,可得三通道扰动运动方程组如下:
(1)
(2)
(3)
式中如a22、a24等所示动力系数可参考文献[13]求得。
将式(1)~式(3)进行Laplace变换,可得到三通道传递函数,如下所示:
(1)俯仰通道
(4)
(2)偏航通道
(5)
(3)滚转通道
(6)
式中,ny、nz为导弹过载,δx、δy、δz为舵偏角。
设定控制系统幅值裕度为6dB,相位裕度为45°,可通过频域分析法设计PID控制参数。
1.2 训练样本获取
通过在表1所示范围内随机改变导弹运动初始状态[x0,y0,z0],目标运动初始状态[xt0,yt0,zt0]与目标侧向机动过载nzt进行10组六自由度仿真,在每组仿真中取1000个弹道特征点处数据,从而获取本文神经网络训练所需样本。

表1 仿真参数变化范围
2 RBF神经网络理论基础
RBF网络于1988年提出后,因其结构简单、收敛速度快和能够逼近任意非线性函数的特性,逐渐地在函数逼近[14]、模型预测[15]、系统辨识[16]和故障分类[17]等领域得到广泛应用。常见的正则化RBF网络具有如下特征[18]:
1)正则化RBF网络的隐含层只要有足够多的隐含节点,则网络对任意非线性多元连续函数具有良好的逼近能力,这意味着正则RBF网络可以作为非线性函数的通用逼近器使用;
2)给定一个未知的非线性函数f(·),总可以选择一组网络权值系数,使得网络对于f(·)的逼近是最优的。
RBF网络采用前馈形式,一般包括输入层、隐含层和输出层,其典型结构如图 1所示。
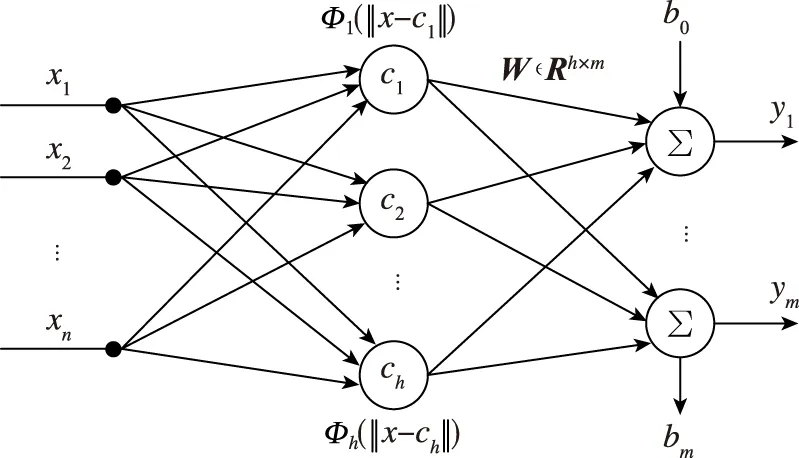
图1 RBF网络结构图Fig.1 The structure of RBF network
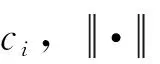
针对图1所示具有n-h-m结构的RBF网络,其输入可表示为x=(x1,x2,…,xn)T,网络中第i个隐含层节点的数据中心值设为ci,径向基函数的宽度设为bi,网络的映射关系可分为2层[19]:
1)从输入层到隐含层的非线性映射,选择Gaussian基函数,则第i个隐含层单元的输出为:
(7)
2)从隐含层到输出层的线性映射,则输出层第j个神经元的输出为:
(8)
3 俯仰/偏航通道神经网络控制器设计
本文所设计的过载驾驶仪中,输入偏差信号、导弹飞行状态与输出控制指令信号之间的关系可表示为函数映射,通过导弹飞行过程中产生的偏差与飞行状态数据对RBF网络进行离线训练以逼近函数映射,离线训练完成的RBF网络可以直接作为控制器使用。
对于俯仰通道而言,神经网络的输入为nyc-ny,输出为舵偏角指令δz;对于偏航通道而言,神经网络的输入为nzc-nz,输出为舵偏角指令δy。两个通道的网络输入层节点数n=1,输出层节点数m=1,而隐含层节点数h需根据网络训练算法确定。
3.1 控制器设计过程
采用Chen等提出的正交最小二乘算法(Orthogonal least squares learning algorithm, OLS)[20]进行RBF网络的离线训练,具体步骤如下:
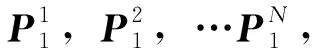

3)在已知训练样本输入数据x、输出数据y与RBF网络数据中心xk后,隐含层与输出层之间的权值与偏移量可以通过广义逆方法求解隐含层输出与样本输出数据之间的线性方程组的方式得出。
4)计算此时RBF网络输出相对于样本输出的均方误差(Mean Square Error, MSE),如果MSE小于目标值,则终止算法,否则进行步骤5。
5)对矩阵H进行Gram-Schmidt正交化,使得矩阵H的第k列正交于第k-1列。
6)重复步骤2~步骤5,直至MSE小于目标值或算法达到最大循环步骤。
3.2 仿真分析
采用本文所设计符合性能要求的PID控制器,通过改变导弹运动的初始条件[x0,y0,z0],目标初始位置[xt0,yt0,zt0]与目标侧向机动过载nzt进行10组六自由度仿真,以获得RBF网络训练所需样本数据,通过每组仿真获得1000组数据,在获得的10000组数据中选取9000组作为训练数据,剩余1000组作为测试数据。设定径向基函数宽度bi=0.8,网络输出误差目标为lg(MSE)<-15,RBF网络设计结果如图2~图3所示。
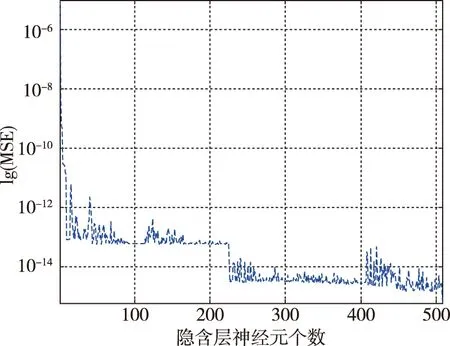
图2 俯仰通道网络MSE变化曲线Fig.2 The MSE in recursions of pitch channel RBF network
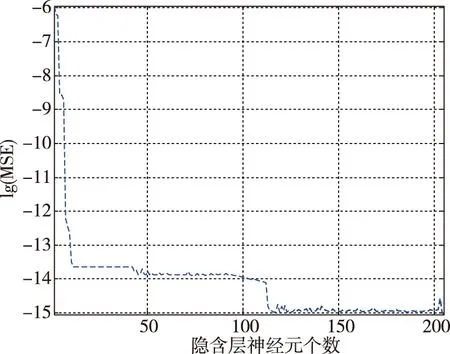
图3 偏航通道网络MSE变化曲线Fig.3 The MSE in recursions of yaw channel RBF network
由图1与图2可知,随着隐含层神经元个数的增加,RBF网络的拟合误差在逐渐减小,对于俯仰通道而言,隐含层节点增加至507个时,lg(MSE)<-15;对于偏航通道而言,隐含层节点增加至204个时,lg(MSE)<-15。所设计的RBF网络均满足精度要求。
利用1000组测试数据对训练所得的RBF网络进行性能验证,结果如图4~图5所示。
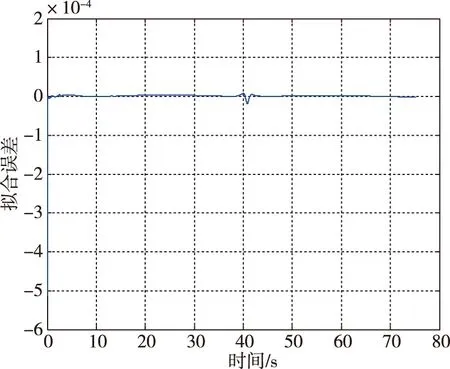
图4 俯仰通道RBF网络拟合误差曲线Fig.4 The RBF network fitting error of pitch channel
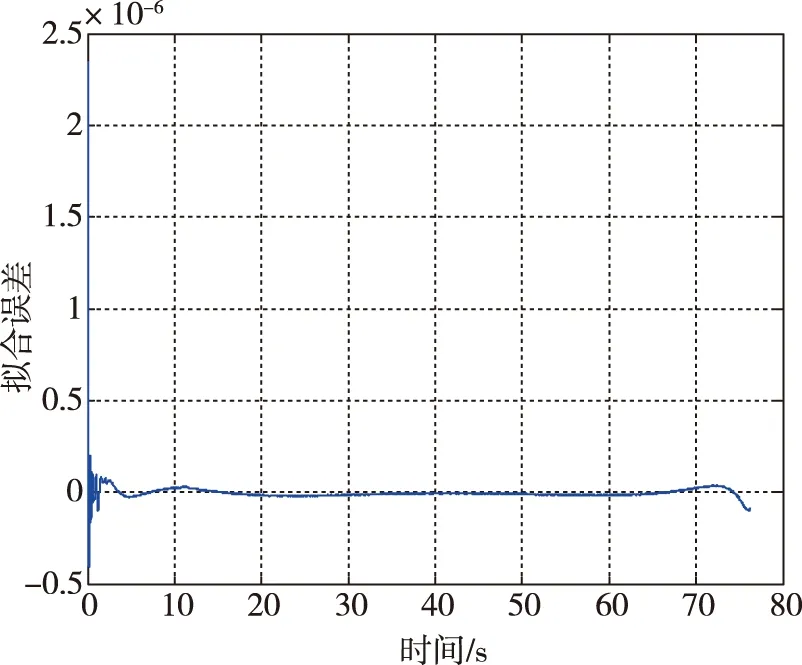
图5 偏航通道RBF网络拟合误差曲线Fig.5 The RBF network fitting error of yaw channel
由以上仿真结果可知,俯仰通道拟合误差最大值在10-5量级,拟合误差平均值在10-8量级。偏航通道拟合误差最大值在10-8量级,拟合误差平均值在10-10量级,见表2。以上结果说明训练所得RBF网络能够很好拟合俯仰通道与偏航通道的控制器。

表2 拟合误差统计
4 滚转通道神经网络控制器设计
4.1 控制器设计过程
滚转通道采用姿态自动驾驶仪的形式,将式(3)转化为状态空间表达式,有:
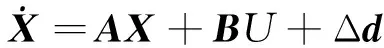
(9)
式中:
Δd为系统非建模动态或扰动量,设其上界为D。
取x1=γ,x2=ωx,将式(9)写为如下形式:
(10)
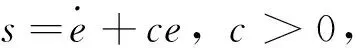
(11)
设计控制律为:
(12)
式中,sign为符号函数。将控制律带入式(11)中,可得:
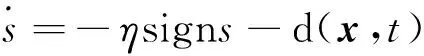
(13)
取η≥D,则有:
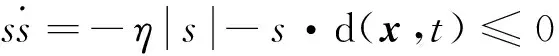
(14)
上述控制律依赖于f(x)的精确性,若由于外部干扰以及系统未建模动态的影响使得f(·)为某一不确定非线性函数,则可以采用RBF网络逼近f(·)来设计控制器。此时RBF网络的输入为γc-γ,输出为f(·)当前取值,网络输入层节点数n=1,输出层节点数m=1,隐含层节点根据仿真寻优选择为h=21。
由式(7)可知,RBF网络输入输出算法为:
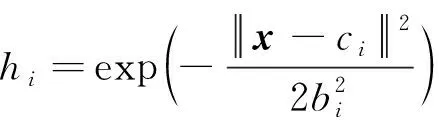
(15)
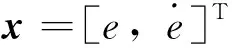
(16)
代入式(12)中,可得控制律:
(17)
将控制律式(17)代入式(11)中,得:
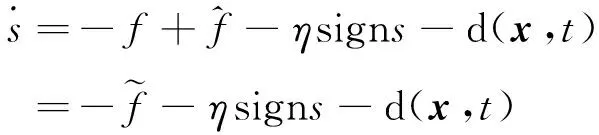
(18)
式中:
设计Lyapunov函数为:
(19)
对式(19)求导,结合式(17)与式(18)可得:
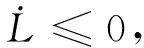
(20)
则有:
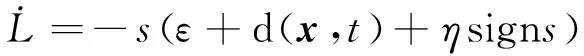
(21)
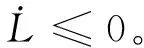
在实际仿真过程中,为克服滑模抖振问题,可采用准滑动模态控制方法[21]。即利用连续的Sigmoid函数θ(s)代替符号函数sign(s),θ(s)的表达式为:
(22)
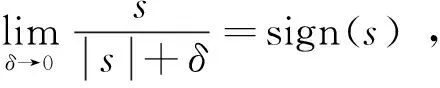
4.2 仿真结果
取30s特征点处滚转通道动力系数,滑模面参数设为c=50,变结构控制项参数η=10,Sigmoid函数中δ=0.05。RBF网络中心向量设置为:ci=0.01×[-1,-0.9,…,0.9,1],径向基函数宽度bi=15,网络初始权值W全部为0;自适应律参数λ=0.015;仿真过程中滚转角指令为γd=15sin(t)deg。在仿真开始1.5s后,在f(x)中加入非线性干扰项,使得f(·)=f(x)+0.1sin(x1)cos(x2)。在不加入RBF网络逼近f(·),即采用式(6)所示的控制律时,仿真结果如图6~图7所示。
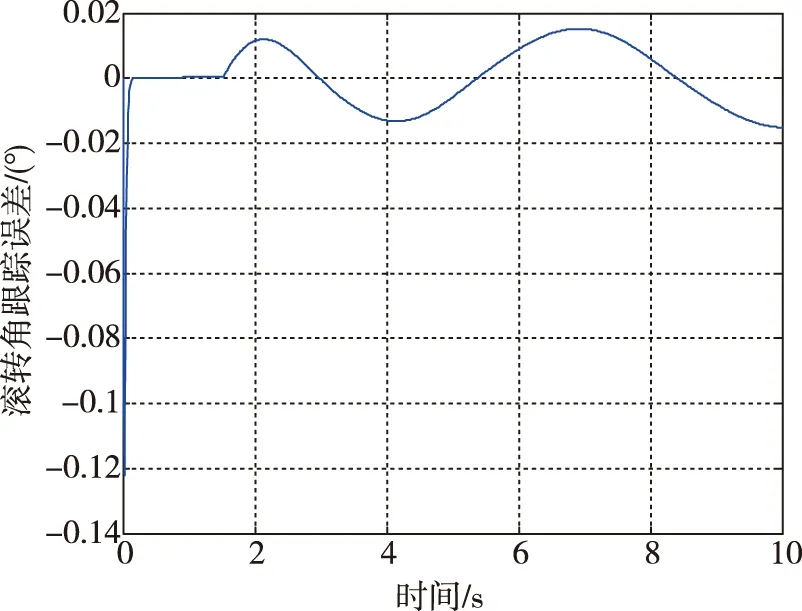
图6 滚转角跟踪误差变化曲线Fig.6 The tracking error of roll angle
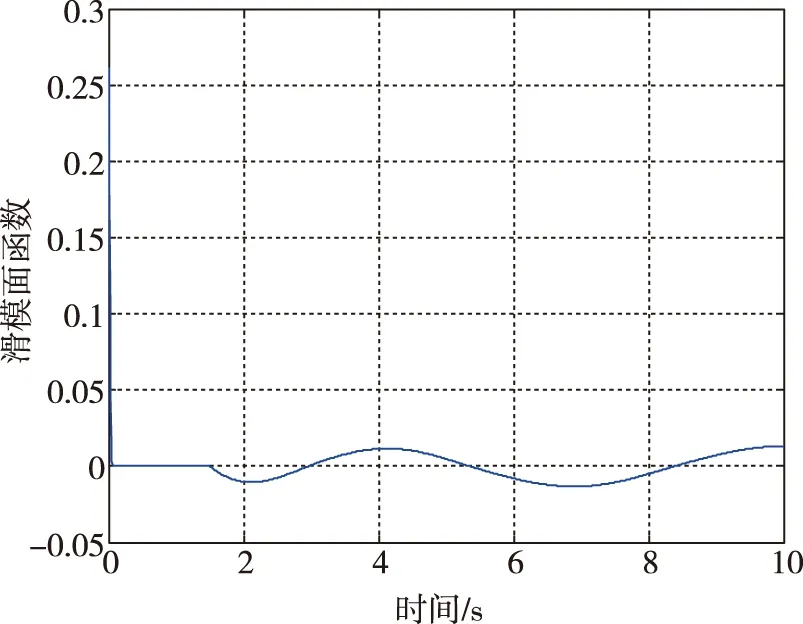
图7 滑模面函数变化曲线Fig.7 The curve of sliding surface function
由图6~图7所示仿真结果可知,在加入外部非线性干扰项后,单纯采用滑模控制不能消除滚转角和滚转角速率跟踪误差,且滑模面也未能收敛至0。在加入RBF网络对非线性干扰项进行逼近,即采用控制律式(11)与权值自适应律式(14)时,仿真结果如图8~图10所示。
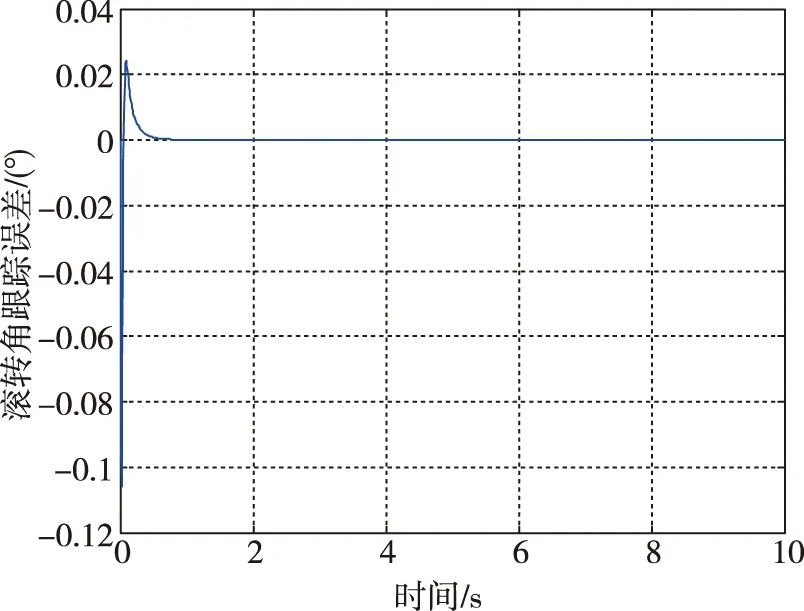
图8 滚转角跟踪误差变化曲线Fig.8 The tracking error of roll angle
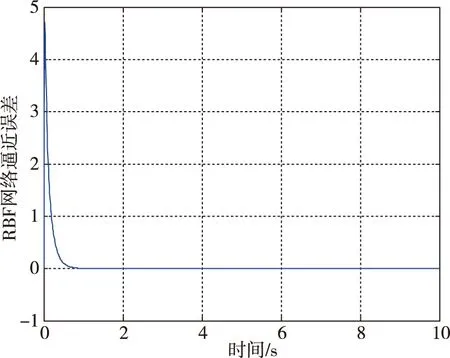
图9 RBF网络逼近误差曲线Fig.9 The approximation error of RBF network
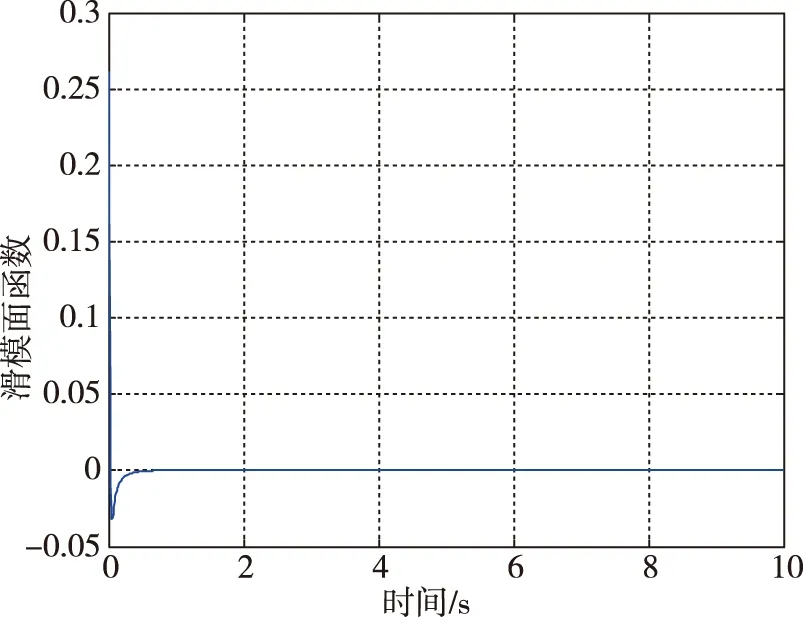
图10 滑模面函数变化曲线Fig.10 The curve of sliding surface function
由图8~图10所示的仿真结果可知,在加入RBF网络的逼近作用后,滚转角跟踪误差在1s内收敛至0,滚转角速率跟踪误差在4s内收敛至0;同时滑模面也于2s内收敛至0附近邻域;在加入非线性干扰项后,RBF网络能够在2s内通过调节权值逼近f(·)。
5 非线性六自由度仿真
本节将所设计的两种智能控制器加入某型倾斜转弯导弹非线性六自由度仿真中,通过对比弹体实际的过载值与过载指令来评估过载自动驾驶仪的控制性能,同时分析滚转角的大小。
导弹初始条件设为:
[v0,θ0,ψv0]=[350m/s,0°,0°]
[x0,y0,z0] =[0,8000,-500]m
[ωx0,ωy0,ωz0]=[0,0,0]rad/s
[ϑ0,ψ0,γ0]=[0°,0°,1°]
目标坐标为[xt0,yt0,zt0]=[15000,0,0]m,速度为[vtx0,vty0,vtz0]=[10,0,0]m/s;并进行侧向机动,机动过载为0.03g,加入所设计的两种智能控制器,仿真结果如图11~图15所示。
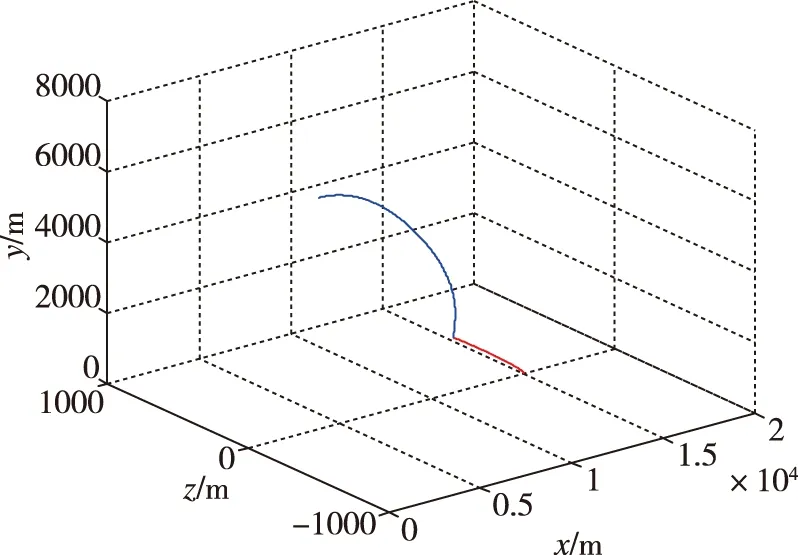
图11 三维弹道曲线Fig.11 The trajectory curve of missile
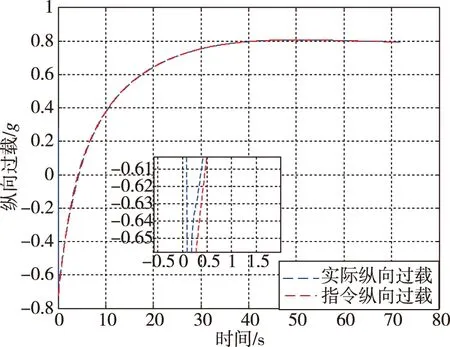
图12 纵向过载跟踪曲线Fig.12 The tracking curve of vertical overload
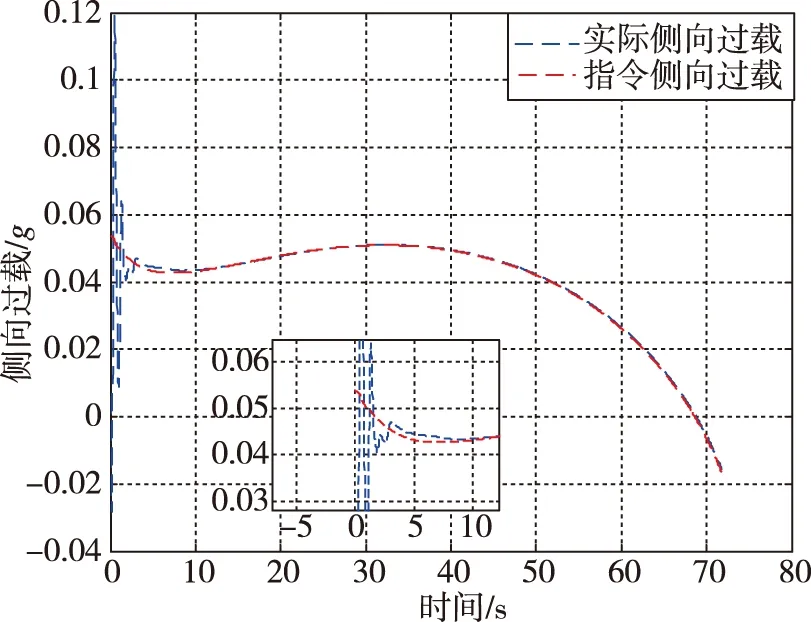
图13 侧向过载跟踪曲线Fig.13 The tracking curve of lateral overload
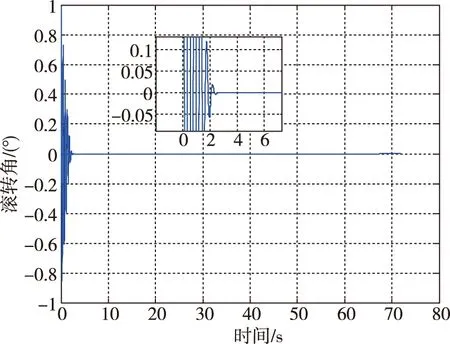
图14 滚转角变化曲线Fig.14 The curve of roll angle
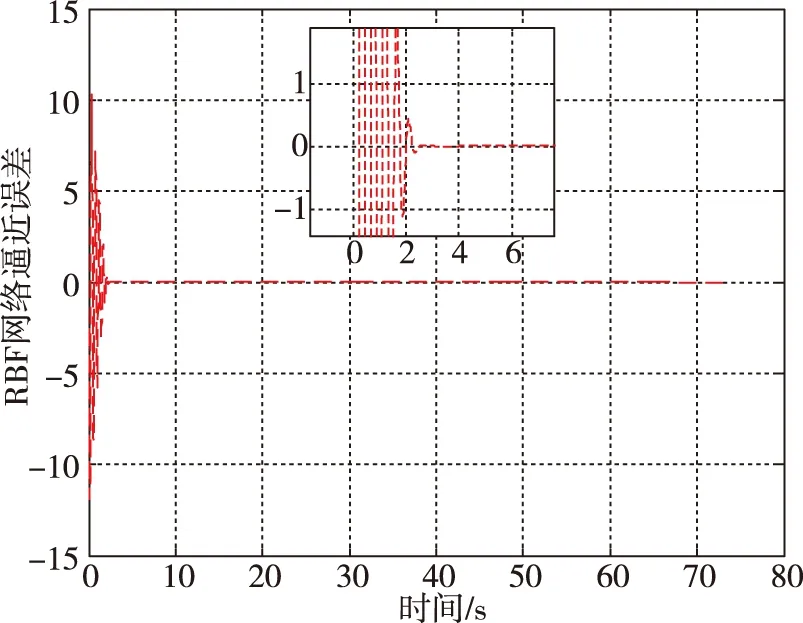
图15 RBF网络逼近误差曲线Fig.15 The approximation error of RBF network
由仿真结果可知,导弹于72.6s成功命中地面机动目标,脱靶量为0.41m,RBF网络逼近误差在仿真开始3s内由于权值调整而出现较大幅度的振荡现象,之后逐渐收敛至0,滚转角也随之收敛到0。纵向过载和侧向过载在3s内均能实现对指令过载信号的稳定跟踪。
6 结论
1) 对于俯仰和偏航通道使用飞行过程中数据对RBF网络进行离线训练,以直接得到神经网络控制器,仿真结果表明,随着RBF网络隐含层神经元的增加,网络对于俯仰通道控制器的平均逼近误差减小至3.4375×10-8,对于偏航通道控制器的平均逼近误差减小至3.2068×10-10。
2) 对于滚转通道利用滑模控制理论,采用RBF网络逼近系统中非线性不确定项,结合Lyapunov稳定性理论推导了RBF网络权值自适应调节律,并证明了所设计控制系统的稳定性。通过滚转通道对指令信号的跟踪仿真说明了所设计控制系统在外界存在非线性干扰的情况下,RBF网络可通过调节权值在2s内逼近干扰项,以提高传统滑模控制器的性能。
3) 通过六自由度仿真验证了所设计的智能控制系统能够控制导弹成功命中地面机动目标。

