次分数布朗运动环境下含违约风险的交换期权定价
王永茂,常竞文
(燕山大学理学院,河北秦皇岛 066004)
交换期权是一种期权持有人在到期日有权但不必须以一种资产交换另一种资产的合约.1978年Margrabe[1]首先给出了交换期权的闭式解,之后众多学者在此基础上修正交换期权定价模型,研究许多在各种限制条件下的交换期权定价模型.
大量实证研究表明,股票市场价格呈现出一种“尖峰厚尾”的分布,并且股价波动在不同时间存在着长相关、自相似等特征,几何布朗运动不能很好地刻画标的股票的这些特性,因此有学者对几何布朗运动进行改进,研究标的资产服从分数布朗运动下期权的定价公式,孙琳[2]利用偏微分方程方法获得了分数布朗运动环境下的期权定价公式.次分数布朗运动是分数布朗运动的进一步改进,Tudor[3]发现次分数布朗运动的退化速度快于分数布朗运动,它能更好地刻画标的资产的长记忆性.Wang等[4]证明了次分数布朗运动环境下的Girsanov定理并得到了次分数Ito公式,肖炜麟等[5]研究获得了次分数布朗运动环境下带交易费用的欧式期权定价公式,并实证分析了定价结果的有效性.郭精军等[6]得到次分数Vasicek随机利率模型下期权价格的闭式解.
Mellin变换是以幂函数为核的积分变换.近年来,有学者利用Mellin变换法对不同类型期权进行定价,Yoon等[7]利用二重Mellin变换得到带有违约风险的欧式期权定价公式,程凤林等[8]运用Mellin变换推出带有交易成本的欧式期权定价公式.
违约风险是指交易对手未能履行契约中的义务而造成经济损失的风险.违约风险模型大致分为两类,一类是违约强度模型,另一类是公司价值模型.刘艳萍等[9]利用无套利对冲原理和公司价值模型得到了具有信用风险的期权定价公式,苏小囡等[10]在违约强度模型下研究了交换期权定价问题,得到了交换期权的闭式解.Ayache等[11]利用数值解方法研究了带有信用风险的可转换债券的定价问题,Wang等[12]利用鞅测度方法获得了既存在违约风险又存在跳跃风险的幂交换期权定价公式的解析解.文中采用公司价值违约风险模型,假设交换期权的两种标的资产与公司资产价值均服从次分数布朗运动,建立资产价格的市场模型,利用二重Mellin变换法获得带有违约风险的资产交换期权的定价公式,并讨论模型参数与期权价格的关系,期望获得更贴近市场的定价结果.
1 预备知识
1.1 次分数布朗运动
次分数布朗运动{ξH(t),t∈R}是Hurst参数为H(H∈(0,1))的连续高斯过程,E[ξH(t)]=0,其协方差为
次分数布朗运动满足如下性质:
( i )自相似.当a>0时,有
( ii )长相依.当H>1/2时,ξH(t)有长期依赖性,即若令
r(n)=cov(ξH(1),ξH(n+1)-ξH(n)),
则
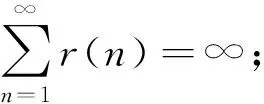
(iii)对任意t≥0和H∈(0,1),有
(iv)当H≠1/2时,次分数布朗运动既不是马尔科夫过程,也不是半鞅;
(v)二阶矩增量的非平稳性:二阶矩增量(假设t>s)为
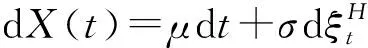
1.2 二重Mellin变换
定义1对于可积函数f(x,y),x,y∈R+,定义Mellin变换M(f(x,y),z1,z2),z1,z2∈C为:
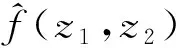
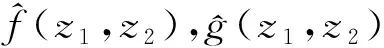
引理2[8]对于复数α和β满足R(α)≥0,令
则
2 资产价格模型及交换期权定价
2.1 带有违约风险的资产价格模型
借助B-S模型的基本假设,提出如下假设:
1)完全市场,无套利机会,无风险利率为常数,无红利支付;
2)资产完全可分,不存在税收和交易费用;
3)交换期权的两种标的资产在测度P下遵循几何次分数布朗运动:
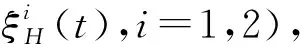
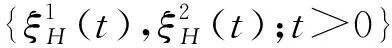
文中研究的信用风险模型是基于公司价值基础上的违约模型,假定资产价值V(t)在测度Q下遵循次分数布朗运动:
(3)
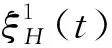
设含违约风险的交换期权到期承诺支付为XT=(S1(T)-S2(T))+,公司破产或违约时到期支付为
XT=((1-α)V(T)/D)(S1(T)-S2(T))+,
其中,常数D为到期时公司的负债;α为破产成本的比率.这里选择D*作为临界值,当V(T) 引理3在次分数布朗环境下含违约风险的交换期权Xt=X(S1(t),S2(t),V(t),t),t∈[0,T],满足的偏微分方程为 证明利用期权价格、标的资产、公司价值三者之间的相关性和对冲原理构造投资组合 Πt=Xt-Δ1S1-Δ2S2-Δ3Vt, 其中Δ1,Δ2,Δ3分别为3种资产份额.在[t,t+dt]时间内,投资组合价值的变化为 dΠt=dXt-Δ1dS1-Δ2dS2-Δ3dVt.(6) 利用次分数Ito公式,求得期权价值的微分,并带入(6)式整理得 定理1在标的资产及公司价值资产服从次分数布朗运动且存在违约风险的模型下,到期日为T的交换期权在t∈[0,T]时刻的价值为 其中 证明为计算方便,减少交换期权价格所满足的偏微分方程的维数.因S1与S2具有线性关系,所以令 X(S1,S2,V,t)=S2X(S,1,V,t)=S2u(S,V,t), 其中S=S1/S2.经等量替换,(7)式中的导数项可表示为 代入(7)式并经过简单运算可得 其中 终值条件为 因此(8)式可将∂u改写为∂un. 进一步可写为 式中 解(10)式得 l=2-22H-1,τ=T2H-t2H. 由定义1并结合(11)式可得 接下来计算(12)式.令 将N(z1,z2)展开得到 其中 对(15)式应用引理2得到 将(16)式代入(14)式进行整理并再次应用引理2得到 (17)式已将B(S,V,τ)转换成不含积分的形式,下面应用引理1与(12)式计算un(S,V,t)的值.因为 因此 下面计算u1,u2,u3,u4.记 结合(17)式并进行等量替换可以得到 其中 同理得到 其中 将u1,u2,u3,u4的表达式代入(18)式,即得到u(S,V,t)的值.将u(S,V,t)转换成X(S1,S2,V,t),即得到定理1的定价结果. 】 参考文献[12],数值模拟中的参数取值如下:S1=100,S2=100,D=80,D*=100,r=0.02,σ1=σ2=σ3=0.15,ρ12=ρ13=ρ23=0.5. 不同期限下给定V=100,α=0.1,利用MATLAB软件,得到不同期限下Hurst指数与期权价格的关系如图1所示. 图1 不同期限下的Hurst指数与期权价格的关系 图1说明,对于相同到期期限的交换期权价值,Hurst指数与期权价格成反比关系,这可以从Hurst指数所对应的时间序列角度分析;Hurst指数越大,其对应的时间序列表现出越强的“长记忆性”,即在某一时间段期权价格的增量预示着下一时间段的价格也有较大可能表现为增量;在相同Hurst指数情况下,期权价格与期限成正比,反映出期限越长,风险越大,从而价格越高. 图2 不同破产成本比率下公司资产价值与期权价格的关系 (a)H=0.25的期权价格变化趋势 (b)H=0.75的期权价格变化趋势 (a)H=0.25的期权价格变化趋势 (b)H=0.75的期权价格变化趋势 给定H=0.75,T=1,得到不同破产成本比率下公司价值与期权价格的关系如图2所示. 图2说明,随着公司资产价值的增加,交换期权价格会有较大幅度的上升,最后趋向于平缓;随着破产成本率α的增加,公司资产价值有所降低,可以解释为破产成本增加导致公司破产风险增加,对应公司的资产价值会降低. 在α=0.1,H=0.25,V=100与α=0.1,H=0.75,V=100两种情况下,比较不同期限及不同Hurst指数下标准布朗运动环境与次分数布朗运动环境下期权价格的差异,得到的关系如图3所示. 在α=0.1,T=1,H=0.25与α=0.1,T=1,H=0.75两种情况下,不同公司资产价值及不同Hurst指数情况下标准布朗运动环境与次分数布朗运动环境下交换期权价格的关系如图4所示. 图3和图4结果均显示,当H∈(1/2,1)时,次分数B-S模型下交换期权价格低于标准B-S模型下的价格,而当H∈(0,1/2)时,次分数B-S模型下交换期权价格要高于标准B-S模型下的价格.由于H>1/2时次分数布朗运动满足“长记忆性”,所以市场变得更加“可预测”,风险变小,期权价值变得更低. 主要研究在次分数布朗运动环境下带有违约风险的交换期权定价问题,在违约风险模型基于公司资产价值基础上,利用二重Mellin变换法求解偏微分方程,得到交换期权定价公式的闭式解,丰富了期权定价的相关结论. 数值模拟的结果显示:① 从次分数B-S模型的角度分析,由于Hurst指数越大,其所对应的时间序列表现出越强的“长记忆性”,序列变得更加可预测,风险相对较低,价格也就有所降低,因而交换期权价格与Hurst指数成反比关系;期限越长,交换期权价格越高.② 从违约风险模型的角度分析,随着公司价值的增加,交换期权价格会有较大幅度的上升,最后趋于平缓;随着公司破产成本率的增加,风险增大,其资产价值会有一定幅度的下降.③ 对比标准B-S模型下交换期权价格与次分数B-S模型下的价格,发现在所研究的两种情况下,次分数B-S模型下交换期权价格都要低于标准B-S模型下交换期权价格,原因同样是次分数布朗运动存在“长记忆性”,这刚好能够更加准确地刻画标的资产的“长记忆性”,具有理论实践价值.2.2 交换期权价格所满足的偏微分方程
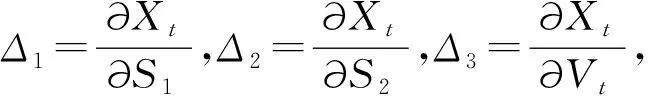
2.3 交换期权定价
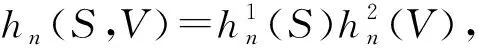
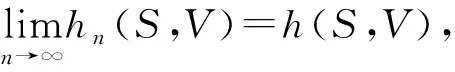
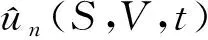
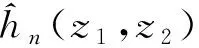
3 数值模拟
3.1 不同期限下Hurst指数与期权价格关系
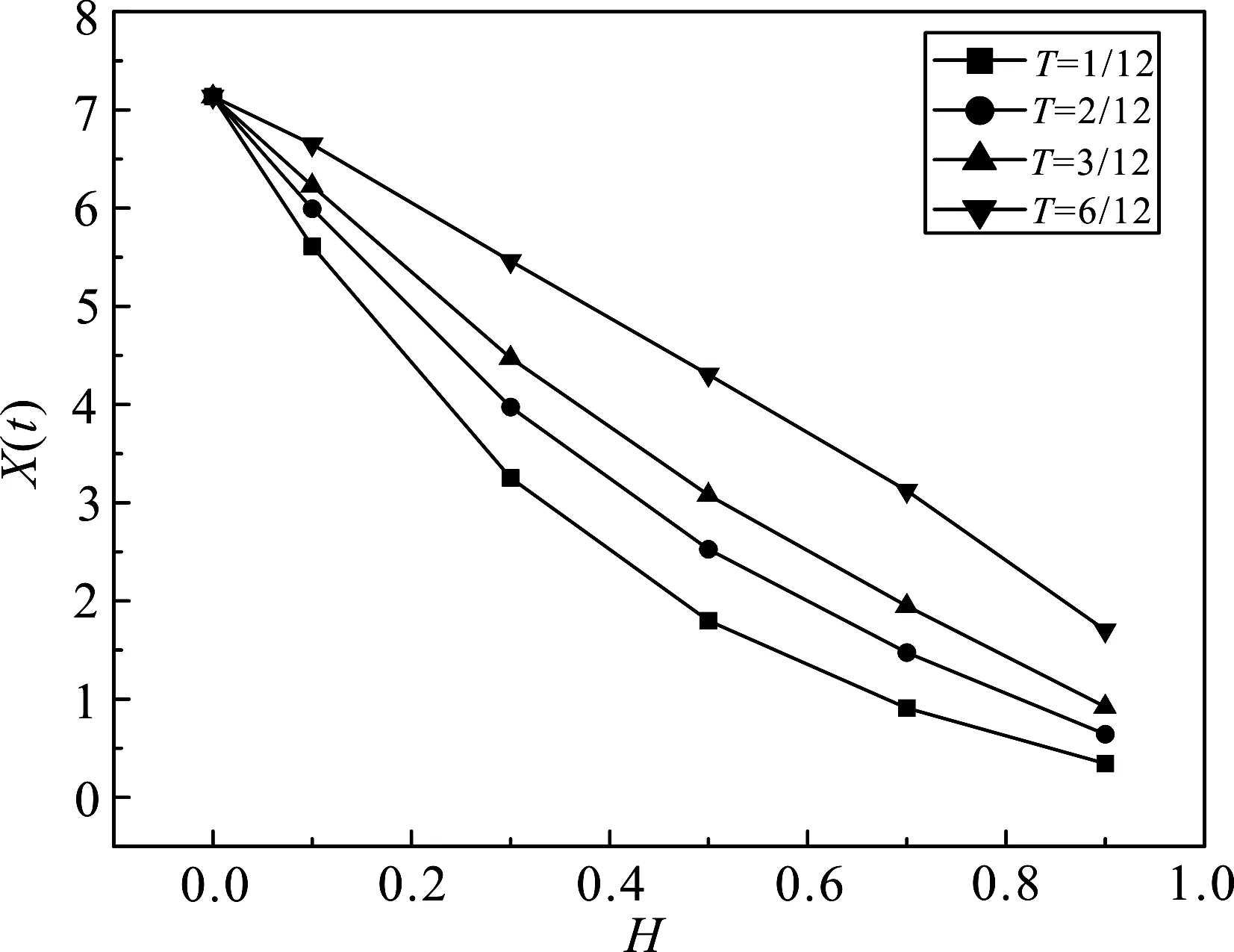
3.2 不同破产成本比率下公司资产价值与期权价格关系
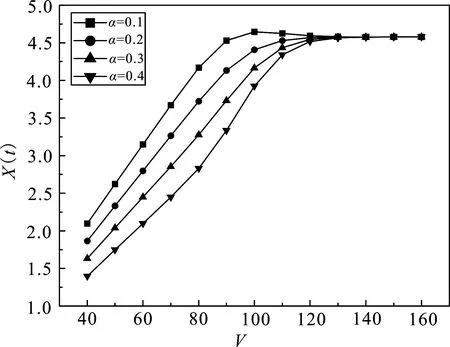
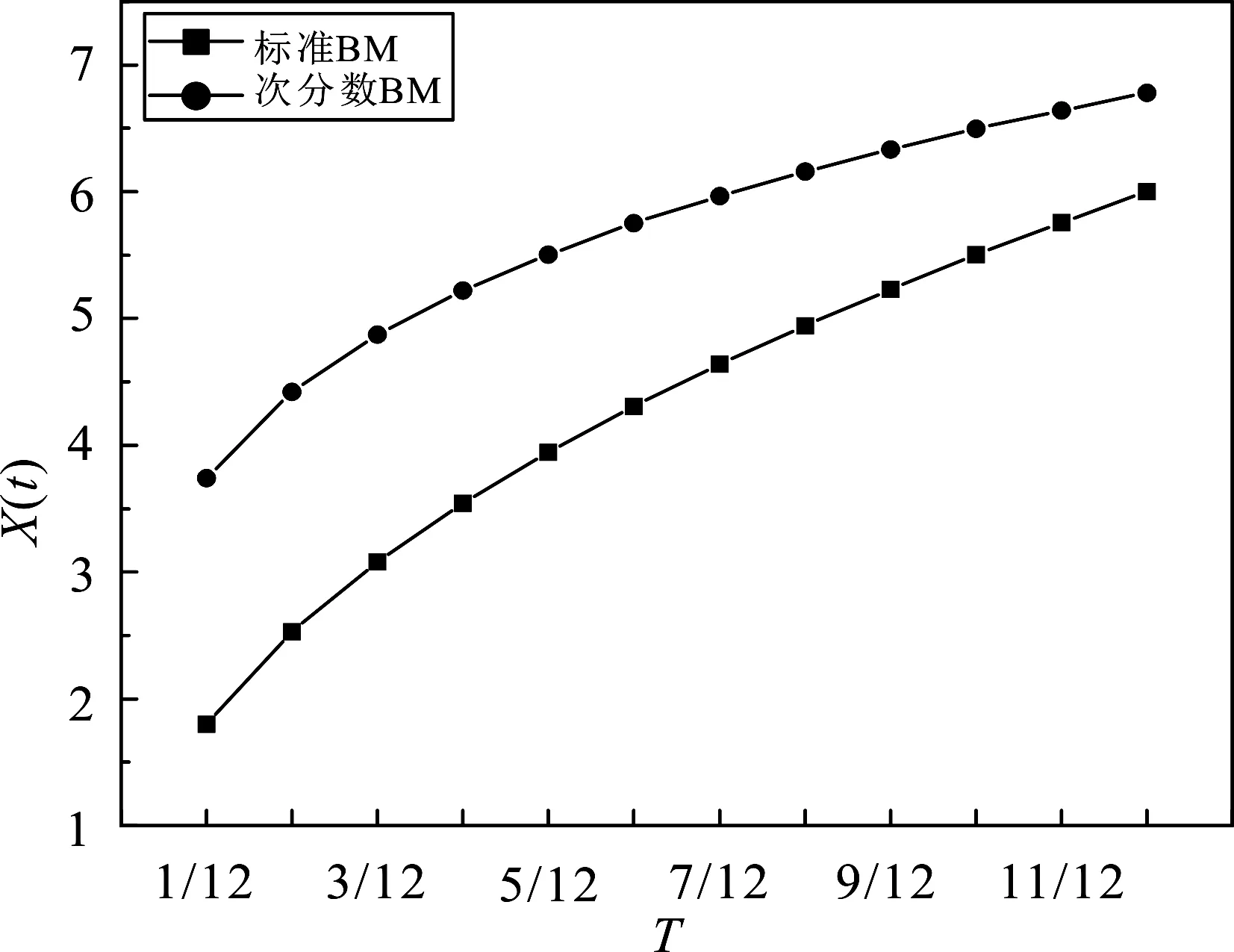

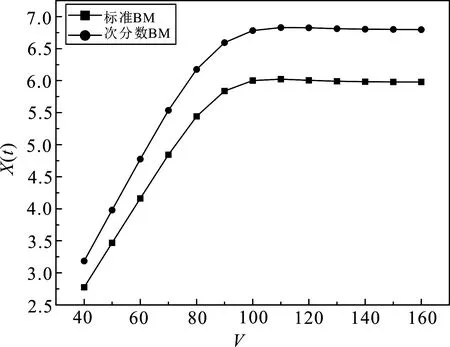
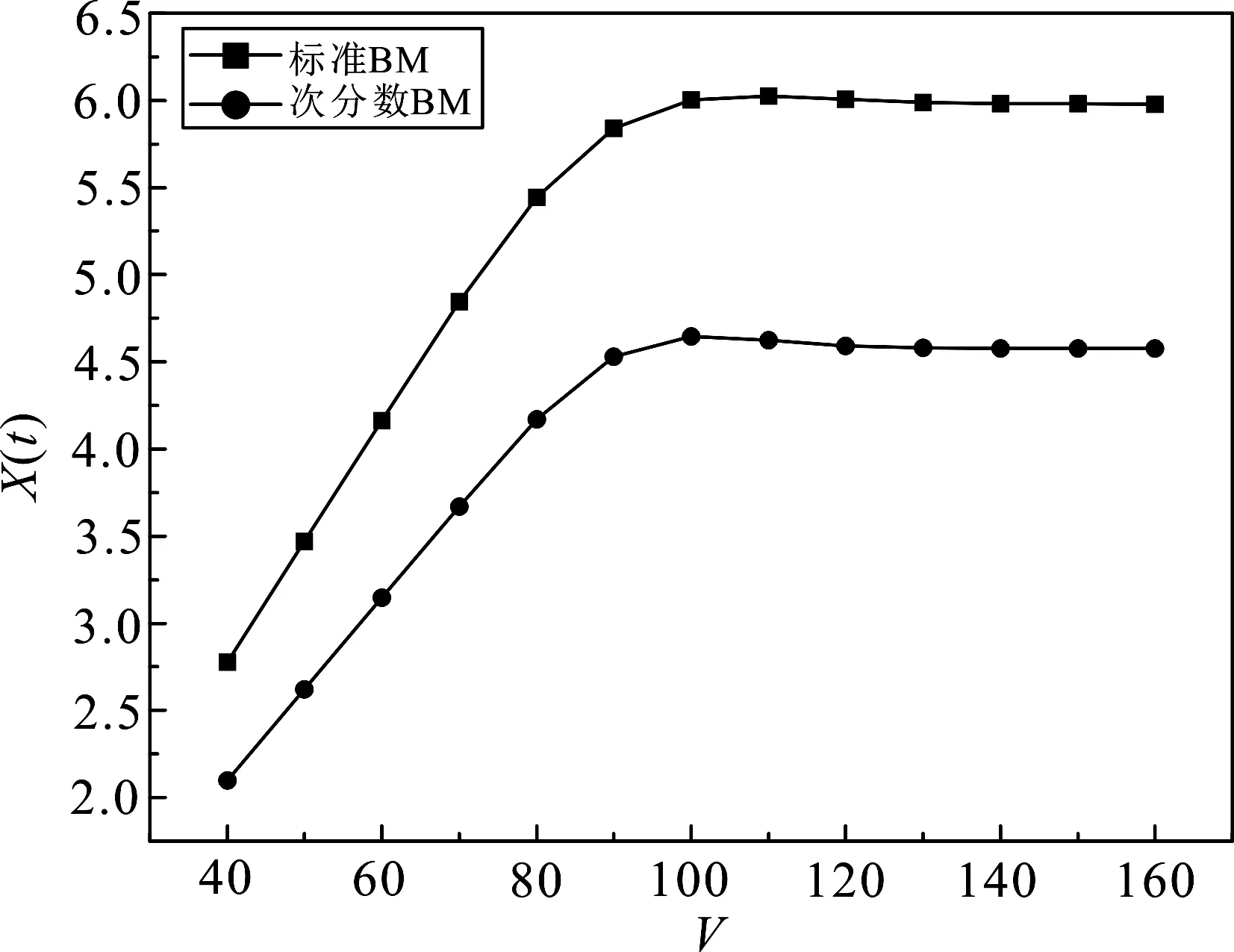
3.3 标准布朗运动环境与次分数布朗运动环境下交换期权价格比较
4 结束语

