采用PPP技术建立高精度GNSS控制网的方法

吴 磊，李博峰，王苗苗

(同济大学 测绘与地理信息学院，上海 200092)

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)技术已逐渐成为现代大地测量的主要手段，被广泛应用于经济、军事、科研和社会生活等诸多领域，对GNSS定位技术在工程应用中的精度需求也越来越高。在以往基线模式的工程控制网建立中，要求严格控制的同步观测，因此需事先设计观测方案且投入大量的人力和仪器设备。传统控制网建立的数据处理主要包括基线解算与基线网平差2步。先利用基线解算软件(如Bernese、Gamit、TGO等)求解基线向量及其协方差阵[1-5]，然后利用控制网平差软件(如TGPPS、科傻等)通过基准约束和坐标变换等过程[6-7]对控制网进行平差处理[8-12]。当前的控制网平差软件通常忽略基线间的相关性，将原本相关的基线视为独立基线处理，导致平差坐标的验后精度虚假偏高。

精密单点定位(precise point positioning，PPP)技术无需同步观测、观测自由、节约成本、且能根据用户的精度需求来调整观测时长；同时，PPP计算简单、效率高，无须考虑传统控制网建立时的基线网构网等复杂过程。因此本文研究采用PPP技术构建控制网的理论和方法，并采用实测数据分析可行性。首先计算所有网点的PPP坐标及其协方差阵信息，然后采用坐标差分的方式构造控制网基线向量，并采用误差传播定律计算对应的协方差阵，最后利用GNSS控制网平差软件解算在给定基准下的点位坐标。为了克服传统控制网平差软件由于忽略基线间的相关性导致平差验后点位精度偏高这一问题，本文提出采用去相关策略对基线网先去相关处理再平差的思想，从而求得较客观的验后点位精度；基于Bernese基线网解模块、自主开发的PPP软件模块、以及TGPPS平差软件，开发了基线解算、PPP解算以及顾及基线网相关性的GNSS基线解算与网平差一体化软件(Tongji Geomatic Office，ToGO)。

1 PPP高精度GNSS控制网建立

以PPP解算的控制网的点位坐标为基础，首先对精密单点定位模型、基线向量及其方差-协方差信息提取、基线向量去相关变换进行了系统的阐述，最后研究了控制网平差模型的基准问题，以及不同基准间平差结果的转换。

1.1 PPP观测模型

为了消除电离层的影响，PPP技术通常采用双频伪距和载波相位无电离层组合观测解算，对应的观测方程为

(1)

(2)

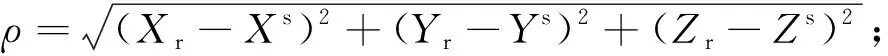
1.2 基线向量及其协方差信息提取

采用Bernese对N个测站进行基线网解算时，会生成N-1条同步观测的独立基线，解算获得的结果文件包含站点坐标及其随机信息。利用基线解算过程中生成的基线组文件(包含基线构成信息)和结果文件可以恢复基线向量及其随机信息。对N个站点同步观测多个时段，即可对多个时段的基线组向量进行平差处理得到平差后的测站坐标[8]。PPP解算同样可得到所有站点坐标及其点位协方差阵，可效仿基线网解恢复基线向量的处理方法，采用坐标差分的方式构建基线向量观测值，生成N-1条同步独立观测基线，并利用误差传播原理计算基线对应的协方差信息。

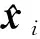
(3)

设控制网测站构成的基线向量组为y，写成矩阵形式为y=Tx，其中T为差分矩阵。通过误差传播定理可以计算基线向量的协方差阵Qyy=TQxxTT，其中Qyy为基线向量网的协方差阵。转换后的Qyy阵不再是分块对角阵，即基线向量间存在随机相关性。

1.3 基线向量去相关性变换

同时段观测的基线间有2种相关性，几何相关性(即图形相关)和随机相关性。Bernese进行基线网解算的预处理过程中，通过站间单差生成同步观测的N-1条几何独立基线(假设有N个测站)。与几何相关性不同，随机相关性通过基线向量协方差阵的非对角元素表现出来。常用的随机软件(如CGO、TGO等)通常忽略该随机相关性，尽管忽略相关性对平差后坐标结果影响不大，但往往导致平差的验后精度虚假偏高。类似地，利用PPP点位坐标构造的基线向量以及基线间同样存在随机相关性。本文提出的控制网平差方法首先对基线网的相关性进行去相关变换。

设基线网平差的观测方程为

(4)

Qyy=LDLT

(5)

式中：L为单位下三角矩阵；D为对角阵。在式(4)两边左乘L-1矩阵得到

(6)

令变换后的向量组观测值z=L-1y，则它对应的协方差阵为Qzz=D。显然，变换的向量组z是独立的，因此采用传统的不顾及基线网相关性的平差软件处理是严密的。

1.4 控制网平差的基准问题

令B=L-1A，将整网误差方程写成

(7)

式中v表示全部GNSS基线向量观测值的残差。3维控制网平差时需要3个位置基准、3个方位基准以及1个尺度基准，而GNSS观测值中包含有方位基准和尺度基准，所以GNSS控制网平差还需要确定位置基准。当网中没有精度较高的起算点时，一般可取某个点单点定位的3维坐标为位置基准，实际上可设该点的坐标改正数为0，可写出基准方程为

(8)

对于无约束自由网平差，式(8)中

(9)

且G阵满足BG=0。

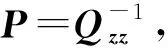
(10)

自由网平差中，选取不同点作为基准的平差结果可以相互转换，令采用点i和点j对应的基准方程(8)的系数阵为Gi和Gj，则相应的平差结果有如下的转换关系[6-7]为

(11)

(12)

对于3维约束平差，基准可以是固定某几个参考站坐标，替换无约束平差的G阵，即可得到3维约束平差的未知参数解和协方差信息。以固定网中前3个点为例，G阵为

GT=[I3×3I3×3I3×303×3…]

(13)

2 软件设计

ToGO软件是严格按照第1节所述数学模型，由C#语言在Visual Studio平台编写。软件具备长-中-短基线解算及控制网平差的功能，可以生成同步观测的独立基线，对所有观测站点进行联合网解。网平差方面，考虑了基线间的随机相关性，可对不同尺度、不同数据处理软件的基线解算结果进行平差。另外，对于PPP模式的控制网，通过坐标差分生成虚拟基线观测值，对虚拟观测值及其随机信息进行去相关变换，实现了PPP解算结果的平差。软件设计的主要流程图如图1所示，对于A、B级基线网，采用ToGO软件平差，可获得毫米级的测站坐标。

3 实验分析

为了验证PPP模式建立控制网的可行性、顾及基线间相关性平差模型的可靠性以及ToGO软件的准确性，分别选取了不同尺度的2个控制网进行实验分析。算例1为美国中部地区连续运行参考站(continuously operating reference stations,CORS)网，距离为30～100 km不等；算例2为亚太地区IGS站构成的控制网，距离为500～1 000 km不等，分别计算了2组数据的基线网解和PPP解，然后使用ToGO软件进行控制网平差。每个算例分别选取了5个时段的全球定位系统(global positioning system，GPS)观测数据进行实验。

3.1 CORS网平差

采用美国CORS中部地区10个站点在2016年上半年5期的GPS观测数据，每期相隔1个月、每个时段12 h，采样间隔为30 s，基线长度为30～100 km不等。网型结构如图2所示，选取MONC、MOPL和MOPN等3个点为基准点，分别对这5个时段的观测数据进行基线网解及PPP解算，得到每个时段的基线组合文件(*.BSL)，解算结果的标准差(standard deviation，STD)统计值为毫米级，然后进行平差处理。

固定MONC、MOPL和MOPN等3个站，利用ToGO软件进行3维约束平差。由于CORS网尺度较小，基线网解平差后的内符合精度数值很小，均在1 mm以内。将数据观测时长分别缩短为6、2 h进行实验，平差后的精度指标在数值上依然是1 mm以内。为了验证基线网解算的坐标准确度以及ToGO平差的可靠性，将平差后坐标与官网提供的参考真值坐标进行比对，统计平差后的坐标误差，如图3所示。从图中可以看出，无论是2、6 h还是12 h基线网解平差后的坐标差值3个方向基本在8 mm以内。因此，在利用GNSS技术建立工程控制网时，若是采用基线联测的方式，2 h观测误差即可达到1 cm以内。

第2节提到，ToGO实现了直接对PPP解算结果进行平差。本文以PPP解算的测站坐标结果为基础，构建虚拟基线向量。与基线网平差的处理类似，固定MONC、MOPL和MOPN等3个站，在此基础上利用ToGO软件进行3维约束平差。图4展示了12、6 h和2 h平差精度统计结果，12和6 h数据忽略相关性的平差精度分别在2～3 mm、3～5 mm，进行去相关变换后的平差精度数值上稍有增大，但不是很明显；2 h数据忽略相关性平差后精度约5 mm左右，进行去相关变换后则为6～9 mm。显然，随着观测时间的延长，其内符合精度越来越高。观测时间较长时，忽略基线间相关性对平差精度影响不大，而观测时间越短，去相关变换后的精度指标下降明显，这可能是基线间的随机相关性随观测时间的延长而削弱。

将平差后坐标与官网提供的参考真值坐标进行比对，统计坐标差值结果，如图5所示。从图5中可以看出，观测时间为2 h，虽然内符合精度很高，但坐标准确度较低，特别是E方向较真值之差约5 cm，适当延长观测时长，其坐标准确度明显有所改善，12 h观测3个方向的坐标较真值之差都可达到1 cm以内。所以在工程项目中，利用基线联测的形式建立控制网，其时间成本较小，但需要更多人力和仪器设备，而通过PPP的方式直接建立控制网则需要足够长的观测时长才可满足控制网的高精度指标。

3.2 IGS基线网平差

实验二数据为亚太地区8个IGS站点，同样是在2016年上半年5期的GPS观测数据，每期相隔1个月，由于IGS站距离相隔较远，故选取了每个时段观测24 h的数据，采样间隔为30 s，基线长度为500～1 000 km不等。网型结构如图6所示，选取其中3个站BJFS、SHAO和SUWN为基准点，分别对这5个时段的观测数据进行基线网解和PPP解，得到每个时段的基线组合文件(*.BSL)，解算结果的STD值为毫米级，然后进行平差处理。

固定BJFS、SHAO和SUWN 3个站，利用ToGO软件进行3维约束平差，通过设定是否考虑基线向量间的随机相关性，得到去相关前后的平差结果，图7、图8第一行分别为24 h观测数据的基线网解和PPP解考虑相关性前后3维约束平差的内符合精度统计结果。从图中可以看出：24 h的观测数据，忽略相关性的情况下，基线网解后进行控制网平差，X、Y、Z这3个方向的平差精度能达到1 mm以内，PPP解的平差精度达到4 mm以内；去相关以后，基线网解的平差精度在1～2 mm，PPP解的平差精度则在5 mm左右。显然，基线网解与PPP解在去相关处理后，STD值在数值上都会有所变大，即忽略基线向量间的随机相关性，会导致其平差精度虚假偏高。

将实验数据分别截取6、2 h进行实验，统计结果分别展示在图7、图8的后2行中。6 h的观测数据，忽略基线间的随机相关性，基线联测平差后X、Y、Z这3个方向的精度在2 mm以内，PPP解平差的精度在5～8 mm；进行去相关变换后，基线联测平差后的精度在3～4 mm以内，PPP解平差的精度在8～15 mm。2 h的观测数据，忽略基线间的随机相关性，基线联测平差后X、Y、Z这3个方向的精度在2～3 mm，PPP解平差的精度在8～15 mm；进行去相关变换后，基线联测平差后的精度在5 mm左右，PPP解平差的精度在15～20 mm。6与2 h的统计结果也能再次验证，忽略基线向量间的随机相关性会使验后精度表现得虚假偏高。特别是在观测时间较短、基线较长的情况下，程序进行去相关变换考虑相关性，测站验后精度会更能反映真实情况。

4 结束语

本文系统阐述了PPP建立高精度GNSS控制网方法，从PPP解算的测站坐标及其随机信息出发，研究了基线向量及其方差-协方差信息提取、基线向量去相关变换以及控制网平差基准等问题。开发了考虑基线间随机相关性的GNSS基线解算与网平差一体化软件ToGO，并设计实验分析验证其平差效果。实验结果表明：

1)2 h以上的同步观测，控制网平差精度能达到毫米级，且中小尺度基线网测站坐标与真值相比误差在1 cm以内；2 h观测计算PPP坐标，再构建基线网进行平差，测站坐标与真值相比误差在5 cm以内，若要达到毫米级需求，则观测时间可延长到12 h。

2)对基线联测或PPP坐标构建的基线网进行平差，忽略基线间的随机相关性，都会导致基线网验后精度虚假偏高，且观测时长越短、基线越长，这一随机相关性对验后精度的影响越明显。

3)对短时间观测的大尺度控制网平差，无论是基线联测还是PPP模式构建控制网，都应该考虑基线间随机相关性对精度评定的影响。