带支腿浮式结构水动力系数快速算法研究

武海浪，陈徐均，黄亚新，沈海鹏，苗玉基

（解放军理工大学 野战工程学院，南京210007）

0 引 言

带支腿浮式结构是指在浮式平台的基础上设计加装一定数量的可升降支腿而形成的海洋工程结构。结构在提桩和放桩过程中，桩腿并不触及海底，主体平台处于带桩腿漂浮的状态。对于一个确定的浮式结构，按照船舶水弹性理论对其进行水动力分析时，一般需要进行湿面网格定义、格林函数分析和水动力响应计算几个步骤[1-5]。要研究水下桩腿长度变化以后的浮式结构的水弹性性质，就要针对变化的参数，重新进行浮式结构的干模态参数计算、重新定义新的湿面网格，然后进行水动力计算。文献[6-8]就是采用了根据水下桩腿长度分工况的方法进行分别计算，认为水下桩腿的长度对浮式结构的水动力系数、波浪激励力以及水动力响应都有显著的影响。

三维线性水弹性分析的核心是格林函数分析，是比较消耗CPU时间的，尤其是当参与计算的面元较多的时候，计算效率会明显地下降。前人对三维水弹性分析算法效率给予了关注，致力于提高计算效率：戴愚志等[9-10]用GMRES（Generalized Minimal RESidual algorithm）方法求解了大型离岸结构水弹性分析所获得的复系数线性方程组，并按照向后误差分析方法给出了它的终止准则。数值试验表明GMRES方法可提高效率，减少计算时间，优于直接方法。Wang等[11]引入两项技术到三维水弹性计算当中，以提高超大型浮式结构水弹性计算的效率。其一是使用新的截断标准来降低格林函数及其导数的分析时间，其二是使用了交互式稀疏求解方法代替高斯方法求解水弹性方程，结果显示有效地提高了计算效率。Wu[12]为了提高水弹性程序的计算效率在其程序中使用了对称复合势方法，这种分析方法也一直沿用至今，所以在后面的分析中，本文也只建立了一半的湿面单元。

浮式结构提桩放桩时只是部分参数在确定的状态下进行了微调，并未发生本质的变化。前面的研究方案尽管直观、易行，但这种参数微调就不得不重新建模、反复分析和重新计算，这似乎并不够高效，每一次新的计算包含了大量的重复工作。若采用这样的计算方案，在这类浮式结构的设计工作中，或许将降低工作效率。本文在研究者所熟知的三维线性水弹性理论体系下，利用格林函数矩阵的性质，针对带支腿浮式结构变参数的水动力系数计算问题提出了一种相对较高效的分析方法，主要是在格林函数分析和线性方程组求解方面作了相关的研究。

1 算法原理

1.1 变物面条件问题

假设弹性浮体周围为均匀不可压缩、无粘的理想流体，流场的运动是无旋的，自由表面波为微幅且带支腿浮式结构在波浪中平衡位置附近作微幅运动，则流场的运动可以在欧拉坐标系中采用三维势流理论来描述。

根据对流场的基本假定，在空间固定坐标系中带支腿浮式结构周围，如图1所示，边界SL+SF+S∞+SB所包围的流场内辐射势定解问题可以描述为：

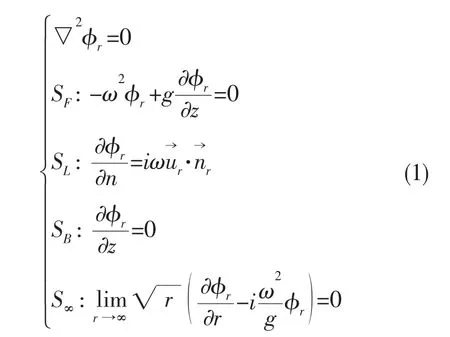
其中：▽2为拉普拉斯算子，φr表示辐射波速度势的空间分量，当浮体在平衡位置附近以入射波圆频率ω，以第r阶干模态振型作单位主坐标幅值振荡时所诱导的流场周围的流体运动速度势。SL为物面边界条件，表示带支腿浮式结构的湿面积，主要由浮式结构平台的底部、侧舷和桩腿三个部分组成。由于桩腿是可以上下移动的，物面条件是可变的，物面条件的改变将导致方程解的改变。SF表示自由面边界条件，S∞为无穷远边界条件，SB为海底边界条件。

1.2 计算方法

假定：（1）带支腿浮式结构中桩腿是平直的柱状结构；（2）忽略因为桩腿的上升或者下放而导致的主体平台水线面的变化；（3）桩腿底板的影响很小。选取带支承腿浮式结构水下桩腿最长L1时为初始状态，即将桩腿尽可能向下放置但不触及海底的状态，物面条件记为SL1。采用格林函数法对结构的初始状态进行水动力分析。

对初始状态进行水动力建模。图2为任意一带支腿浮式结构，此时桩腿处于水下伸长状态，湿面网格分为船身主体部分和桩腿部分。整个结构一共划分的单元数记为N，主体平台单元编号记为1～Nhull，后面Nhull+1～N个编号给桩腿。对桩腿湿面元编号原则参照表1，桩腿湿面元编号的方法总体上遵循了以水深为标尺，编号大小遵循“由上到下”的原则。即离水线面向下越远的面元，编号越靠后，竖直方向上，处于同一高度的面元编号越为接近。

表1 桩腿状态编号及湿面元编号Tab.1 The numbering schedule of the wetted panels

桩腿处于初始状态时，经开拓后场内任一点P的辐射势可按源分布表示为：

其中：G（ P， ）Q 为格林函数，应由初始物面条件SL1决定。使用文献[12]给出的有限水深无航速问题的三维脉动源格林函数，其级数表达形式为：

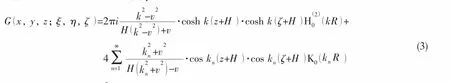
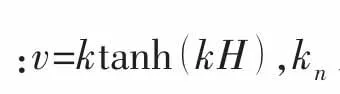
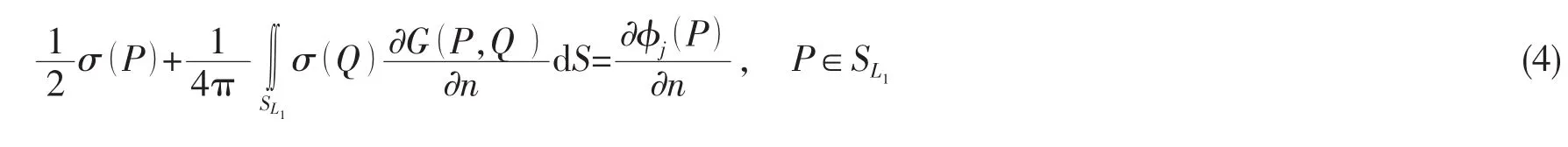
积分方程离散为一组线性代数方程组，表示为：

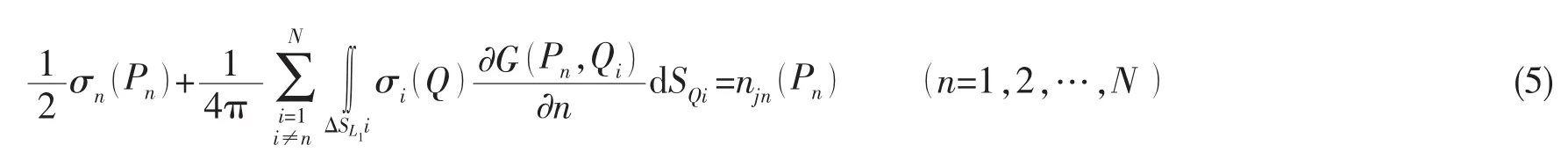
上式可写成矩阵形式，有：

其中：

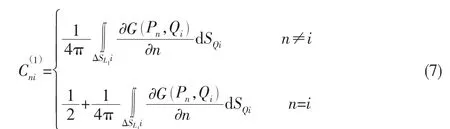
当桩腿同时缓慢、均匀地由初始状态长度L1恰好抬升到Li时，从实际效果上看是桩腿的水下长度变短。若重新进行水动力建模以及新的格林函数分析，可得到新的格林函数矩阵Gnew和新的影响矩阵Cnew。

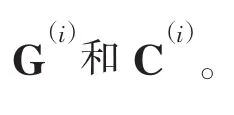
其中：g′和c′分别代表桩腿底部的面元的影响。基于假定（3），可以认为桩腿底板的作用很小，忽略矩阵中g′和 c′在矩阵中的影响，即：

这样，当桩腿由初始状态连续地作抬升动作时，可以视为格林函数矩阵规模不断缩小的过程，即连续地有矩阵中相应的行列退出计算。如图4（b）所示，根据编号法则，位于桩腿底部面元的行列编号靠后，当桩腿由初始状态作抬升动作时，等效于桩腿底部面元退出计算，相应的就是将格林函数矩阵中靠右的部分一层一层地剥离矩阵。直到桩腿全部抬升起来，等同于编号为Nhull+1～Nn-1的网格退出计算。这样有规律的按编号进行矩阵缩减可以得到一系列格林函数矩阵，实际上是给出了流体域内速度势定解问题中物面由SL1逐步变化到SLn的方程组的近似格林函数解。可用公式表示为：

格林函数及其影响矩阵的变化过程表示为

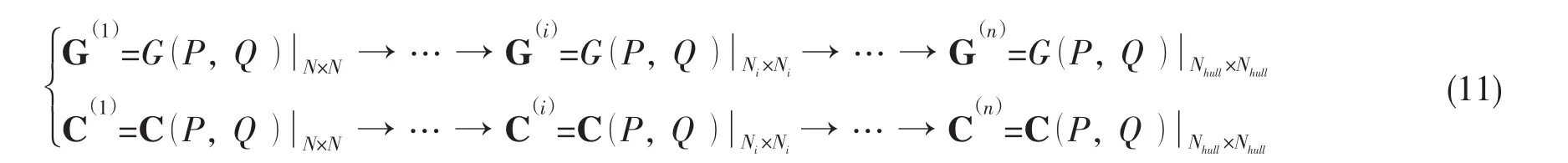
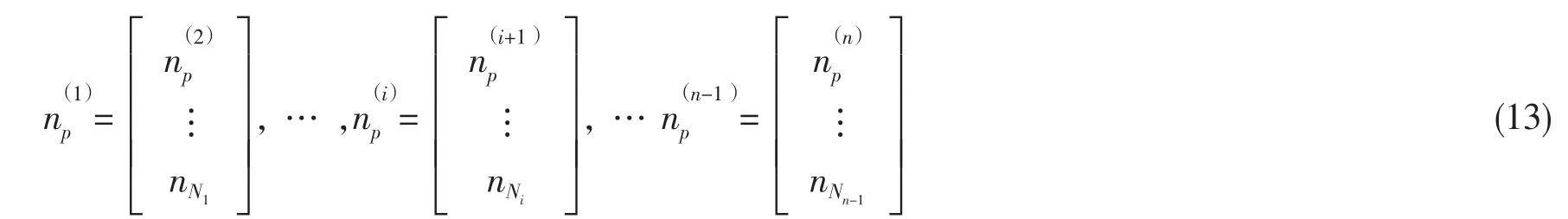
在湿面上进行源强积分计算，可得到辐射势：

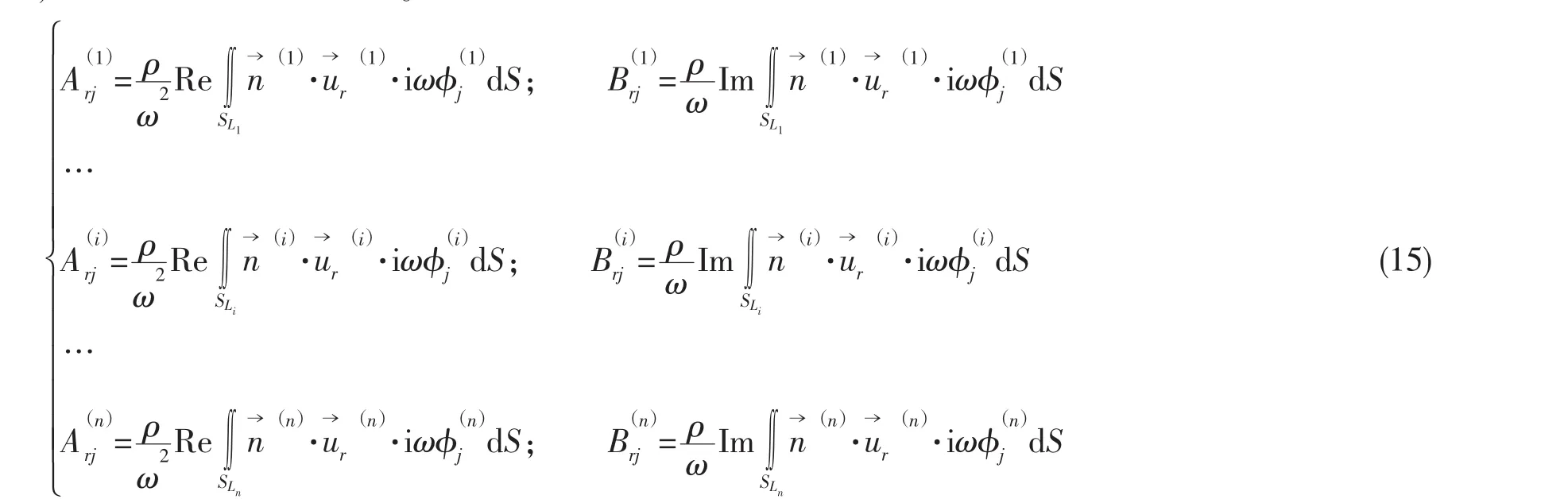
以上便为带支腿浮式结构水动力系数快速计算的原理。根据算法原理，编写程序，成为带支腿浮式结构水动力系数快速计算子模块。

2 算例介绍

选取某型带支腿浮式结构为研究对象，结构长度约为130 m，宽38 m，型深8 m，吃水4 m。将主体平台简化为一个浮箱，6个升降腿分布于全船两侧，每个桩腿高68 m，截面为4 m×4 m方形。使用格林函数分析方法，分两种方案计算水下桩腿长度为10 m，20 m，30 m，40 m和50 m时该型带支腿浮式结构的水动力系数。

第一种方案采用分工况法计算。按桩腿长度建立5种工况分别进行水动力建模。如图5所示，最短为工况1，最长为工况5（工况2～4图略）。所研究的浮式结构是对称结构，只需要定义一半湿面单元，即可进行水弹性分析。这样，工况1就有265个面元；工况2时有289个面元；工况3为313个面元；工况4为337个面元；工况5为361个面元。使用水弹性程序对五种工况分别进行数值计算。

第二种方案采用以矩阵缩减为核心的快速算法计算。以浮式结构的桩腿向水下伸出50 m，即工况5为初始状态，快速计算当水下桩腿长度为40 m，30 m，20 m，10 m时的水弹性响应。

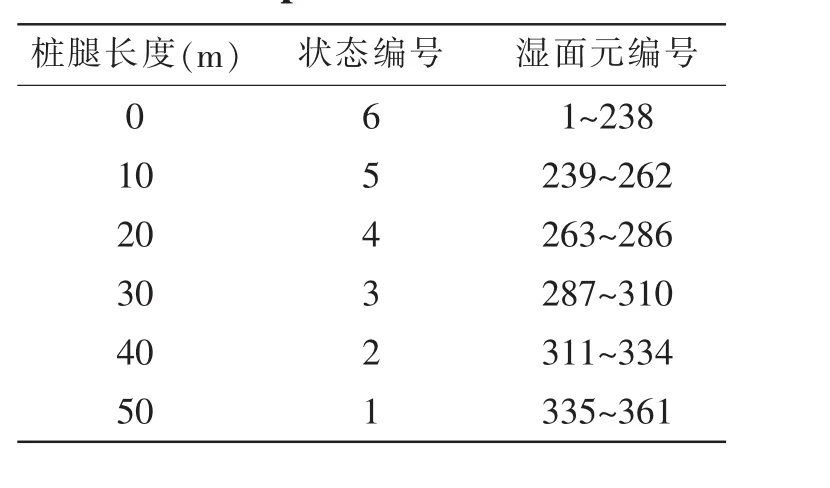
表2 桩腿状态编号及湿面元编号Tab.2 The numbering schedule of the wet panels

整个浮式结构处于初始状态时共有361个湿面元，对已经划分好的湿面元网格进行编号，浮式结构主体部分编号为1～239，对桩腿部分面元主要按照由浅及深，由大及小的原则。表2说明了算例中对桩腿编号的规律。处于桩腿50 m处的湿面元组的编号为355～361，其状态定为1；处于桩腿10 m处的面元组编号为239～262，其状态编号为5。

3 结果检验

3.1 计算精度分析

如图6～11，在坐标平面上，有一系列的散点，每一个点的横坐标表示快速算法结果，纵坐标表示普通算法结果，通过衡量图中点与直线y=x的位置来判断快速算法结果和一般算法结果的相符程度，其中（a）图为附加质量，（b）图为附加阻尼。每一幅图中各有四种颜色的点，分别代表带支腿浮式结构的桩腿处于四种长度，在图的右下方的方框内进行了说明。每一幅图左上方标有一个4×3的数据矩阵。其中一行代表一个固定的桩腿水下长度；一列代表两组计算结果定量的误差分析结果，共有三列，分别为平均相对误差（EAVE），均方相对误差（RMVE）和相关系数（CC）。其计算方法为：

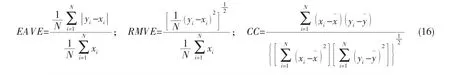
对比分析通过快速算法得到的前六阶刚体模态的水动力系数。如图6，图7和图11所示，纵荡、横荡和艏摇的水动力系数散点与直线y=x重合程度极高，这说明对这三种刚体模态来说，快速算法结果和普通算法结果相符程度极高。计算得到的平均相对误差、均方相对误差和相关系数上也证实了这样的结论，这三种模态的平均相对误差和均方相对误差都在0.5%以下，而两者之间的相关系数都在99%以上，可以认为采用快速算法得到的结果与普通算法结果一致；

和前面这三个刚体模态相比，能够看到垂荡、横摇和纵摇三个模态相对应图中的散点相对直线y=x有明显的偏移，如图8，图9和图10所示，这表明快速算法结果和普通算法结果有一定的误差存在，从数据上看，这几个模态的平均相对误差、均方相对误差几乎都在1%以上，桩腿处于10 m时的横摇附加阻尼系数误差达到了7%，如图9（b）所示，误差明显增高；注意到图中的散点位置高于直线y=x，如图10（a）所示，这说明，和普通算法相比较，快速算法在一定程度上低估了横摇、纵摇和垂荡的附加质量和附加阻尼。

同时，这三幅图中误差统计量表明，快速算法结果的误差随着桩腿长度变短而增大，如图9（b）中的数据，当桩腿为40 m时，平均相对误差为1.4597%和0.3421%，当桩腿长度处于10 m状态时，这两个数据增加到7.1231%和1.4454%。原因在于普通算法中针对桩腿不同长度时的浮式结构分别进行水动力建模，桩腿的底部加了底板，使结构物封闭。而在快速算法中，在进行矩阵拆解时，这部分湿面元没有参与计算，不包含桩腿底板的信息。当桩腿长度较长时，浮式结构的整体湿面积相对较大，底板的影响偏小；而当桩腿长度为10 m时，尽管桩腿底板的面积并没有变化，但是浮式结构的整体湿面积变小了，桩腿底板在湿面积中占有的比例变大，因此底板影响就显现出来了。

3.2 计算效率分析

表3给出了分工况方法和快速算法耗费的CPU时间统计。在算例中一共分析了200个频率，20个模态（包含14个弹性体模态）。

表3 CPU计算时间统计表Tab.3 Statistics of CPU time

当使用分工况法进行分析时，计算工况5耗时67 min；从工况1到工况4的计算时间和为208 min；当使用快速算法进行分析时，工况5被选为初始状态，分析时间与传统方法一致，但工况4到工况1的结果为一次性算出，消耗CPU时间为16 min，和前一种分析方法相比较，一共节约192 min，效率提高了92.3%。这还只是统计的在计算机上的绝对计算时间，尚不包括网格划分、参数定义等前期手工准备时间。计算效率有显著的提升。效率提高的主要原因在于后续的分析主要是在进行矩阵的缩减，实际上是在对电脑中已有的数据进行行变换和列变换，而之前方法的计算主要是进行格林函数分析和格林函数偏导数的分析，这样节约出了大量的机时。若湿面网格划分更多，格林函数矩阵的规模更大，计算效率或许将进一步提高，算法的优势将进一步体现。

4 结 论

本文在三维势流理论体系下，利用格林函数矩阵的性质，针对带支腿浮式结构变参数的水动力系数计算问题提出了一种相对较高效的方法。将求解格林函数的过程视为格林函数矩阵G和影响矩阵C矩阵规模减小的过程，即水下桩腿任意长度为Li时的格林函数矩阵和影响矩阵中包含着L＜Li时的信息。这样在进行下一步计算的时候，可以通过上述已经确定下来的编号找到退出计算的网格，对其进行消除，而将已有的信息保留下来，而不必重复计算，从而达到简化计算的目的。本文还给出了通过快速算法计算结果的误差和快速算法的效率。

结果表明：快速算法所计算的刚体的纵荡、横荡和艏摇三种水动力系数与普通算法结果一致，可完全反应这些模态的水动力特性；快速算法所计算的垂荡、横摇和纵摇三种刚体模态的结果与普通算法有较小的误差，但基本可以反应这些模态的水动力特性；当使用格林函数矩阵缩减法进行分析以后，算例的计算效率可以提高92%以上，非常可观。