激电效应对海洋可控源电磁响应的影响
丁学振 李予国*② 刘 颖②
(①中国海洋大学海洋地球科学学院,山东青岛 266100; ②海底科学与探测技术教育部重点实验室,山东青岛 266100)
1 引言
海洋可控源电磁法(Marine Controlled Source Electromagnetic,MCSEM)是探测海洋油气资源和天然气水合物以及其他矿产资源的一种海洋地球物理勘探方法[1,2]。频率域MCSEM通常使用移动的几十至几百米长的电偶极源,利用多个海底电磁采集站采集电磁场数据。进行MCSEM勘探时,先将海底电磁采集站投放至海底,然后拖曳电偶极源在海底电磁采集站上方30~100m处沿测线航行,并发射低频(0.1~10Hz)电磁信号。海底接收到的信号主要来自海底地层的电磁感应信号,其振幅和相位与海底地层的电阻率有关。在MCSEM资料解释中,一般不考虑岩(矿)石的激电(Induced Polarization,IP)效应,因此电阻率被认为与频率无关。实际上,由于激电效应的影响,电阻率是一个与频率有关的复数[3]。在处理MCSEM资料时,如果不考虑激电效应,可能会带来较大误差,从而影响最终地质解释结果的可靠性。
20世纪70年代以来,很多人致力于激电效应的研究。Ware[4]首次对天然场源激电法的可行性进行了探讨,之后国内外陆续开始研究天然场源的激电效应[5-12]。目前,对于从天然场源实测数据中提取激电参数的可行性存在两种不同的意见。罗延钟等[10]认为,地下导电性不均匀所引起的电磁场异常远大于激电效应引起的异常,提取被强大的电磁异常“淹没”的弱小激电异常难度极大。李金铭等[11]采用Dias模型表征地下介质的激电效应,讨论了中间层为极化层的三层水平地层模型天然电磁场激电响应特征,并给出一个已知铅锌矿区的试验结果,认为从天然场源响应获取激电信息是可行的。曹中林等[12]将Cole-Cole模型应用于大地电磁法,对于中间层为高极化率的三层水平地电模型,分析其极化参数对正演响应的影响特征,并对实测数据进行反演计算,在实际的油气检测中取得了一定效果。董莉等[13]基于自适应差分进化算法,实现了MT信号激电信息的提取。曹金华等[14]研究了同时存在激电效应和电磁效应时的复电阻率特性,通过正演模拟,总结出不同的电磁耦合效应对视电阻率及视相位的影响规律。
为了克服天然场源信号弱、抗干扰能力差的不足,人们研究了可控源音频大地电磁(Control Source Audio-frequency Magnetotellurics,CSAMT)激电效应;岳安平等[15]分析了不同的激电响应模型,并探讨了从CSAMT资料中提取激电信息的方法。汤井田等[16]讨论了CSAMT中激电效应对不同地电断面类型的影响,为从CSAMT资料中提取激电信息提供参考。徐汶东[17]基于Cole-Cole模型,探讨了激电参数对激电效应的影响,并提出了基于最小二乘的激电参数提取方法。相比磁场分量,电场分量对激电效应反应更灵敏;基于这一特点,王珺璐[18]提出了分步反演提取激电效应的方法;徐玉聪[19]分析、总结了含激电效应的不同水平层状地电模型的响应特征,并采用自适应正则化反演方法,实现了一维CSAMT激电参数的反演计算;张锐锋等[20]基于等效介质理论激电(GEMTIP)模型研究了时频电磁法的时域激电参数提取,并应用于实际资料;黄逸伟[21]基于Cole-Cole模型,计算了含激电效应的CSAMT三维正演响应,分析激电参数对CSAMT响应的影响;陈帅等[22]将Cole-Cole模型加入一维瞬变电磁正演计算,并实现了一维瞬变电磁复电阻率反演算法。
在MCSEM激电效应研究方面,郭宁宁等[23]基于Cole-Cole模型研究了激电效应对电磁场的影响,并提出了反演激电参数的方法;王德智等[24]总结了油气藏产生激电效应的两种模式,并分析了各参数对两种模式下激电响应的影响特征,以及两种极化模式共同作用下的激电效应特征。有关MCSEM激电效应的研究成果较少,相关研究一般是基于一维模型进行的,且未分析观测频率等参数与激电效应强度之间的关系。
本文基于Cole-Cole模型,在一维和二维MCSEM正演模拟中考虑激电效应,计算电磁场响应及IP强度,分析激电效应的强度与观测频率、油气储层厚度、埋深等参数之间的关系; 研究了激电效应对一维MCSEM反演结果的影响,将含有激电效应的正演数据分别用考虑激电效应和不考虑激电效应的反演程序进行反演,具体分析了激电效应的影响。
2 方法原理
2.1 考虑激电效应的正演理论
前人提出了很多描述岩(矿)石激电效应的模型,如Cole-Cole模型[25]、Dias模型、Wait模型等。基于被广泛应用的Cole-Cole模型,Pelton等[26]通过对岩(矿)石基本结构的研究和对大量岩(矿)石标本、露头的测量结果,对其进行了改进。张赛珍等[27]通过测量岩(矿)石标本的激电频谱,证实了该模型可近似代表实际情况。Cole-Cole模型的等效电路如图1所示,图中Ra、Rb均代表电阻器, (iωx)-c表示电容器,其表达式为
(1)
式中:ρ(iω)为复电阻率,ω为角频率;ρ0为零频电阻率;η为极化率;τ为时间常数;c为频率相关系数。基于罗延钟等[10,28]关于分散浸染状矿化体及天然场源激电效应的研究和Pelton等[26]对岩(矿)石露头的实测结果,本文模拟计算时假定激电时间常数τ和频率相关系数c分别为2.0s和0.25。
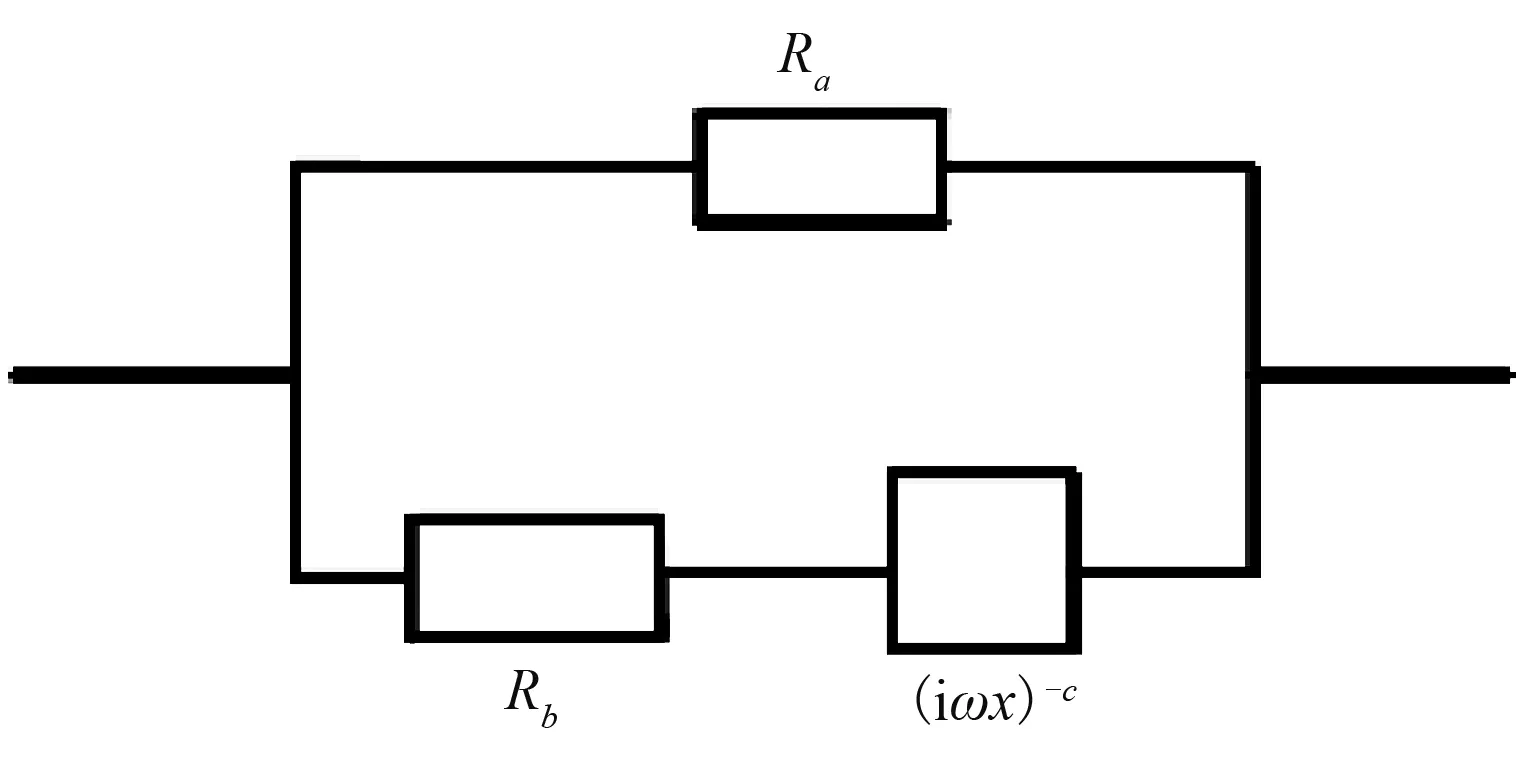
图1 Cole-Cole模型等效电路
假设时谐因子为e-iω τ,在似稳态情况下,考虑激电效应的麦克斯韦方程组可写为

(2)

(3)
式中:E为电场;H为磁场;Js为电流密度;μ0为介质磁导率;σ(iω)为复电导率,即1/ρ(iω)。
当地下介质为一维水平层状介质时,先利用双重傅里叶变换和矢量势函数将麦克斯韦方程组从空间域转换到波数域,并求得波数域电磁场响应,再利用数字滤波法实现正、余弦变换,求得空间域电磁场响应[29]。对于二维地电模型,关于构造走向方向做傅里叶变换,将电磁场边值问题转换为波数域2.5维问题,采用交错网格有限差分法,基于一次场/二次场分离方法导出波数域二次场离散形式,并进一步求得波数域电磁场,再对波数域电磁场做傅里叶逆变换,获得空间域电磁场响应[30,31]。
2.2 IP强度
郭宁宁等[32]、王德智等[24]用极化电场对非极化电场的归一化振幅值EN表示电场振幅的激电特征,用极化电场与非极化电场的相位差ΔΦ表示电场相位的激电特征,即
(4)
ΔΦ=Φ极化-Φ非极化
(5)
式中:E极化和E非极化分别表示极化电场和非极化电场;Φ极化和Φ非极化分别表示极化电场和非极化电场的相位。
为了直观地表示激电效应的强度,本文借鉴有效异常[33]和可探测度[34]的计算方式,定义一个表示激电效应强度的物理量——IP强度。该参数不仅包含振幅信息,且包括相位信息,其表达式为
(6)
(7)
式中 IPE、IPH分别表示电场和磁场的IP强度。
2.3 反演方法
2.3.1 目标函数
本文反演采用高斯—牛顿法[35],其目标函数为
φ(m) =φd(m)+λφm(m)
=‖Wd[dobs-F(m)]‖2+λ‖Wmm‖2
(8)
式中:φd(m)为数据拟合泛函;φm(m)为模型稳定泛函;m为模型参数,是由反演模型各层电阻率的对数组成的向量;λ为正则化因子;dobs为观测数据;F(m)为正演响应;Wd为数据加权矩阵;Wm为模型加权矩阵,本文用最小梯度支撑泛函[36]构建此矩阵。
数据加权矩阵Wd为与数据标准差有关的对角矩阵,其表达式为
(9)
式中:ξ为与仪器本底噪声有关的极小量,该极小量能够防止电磁数据振幅过小的情况[37];ei为第i个数据的估计误差,其表达式为
(10)
式中:erel为电磁场振幅的相对误差,通常假定为振幅的5%;eabs为激发—接收系统的本底噪声,假定电场本底噪声为1.0×10-15V·m-1,磁场本底噪声为1.0×10-18T;erot为由海底电磁采集站方位不确定性引起的误差。
2.3.2 目标函数的极小值
在高斯—牛顿反演中,通过求取目标函数的极小值可以得到搜索方向,下一次迭代的模型参量可表示为
m(k+1)=m(k)+[Hs(k)]-1g(k)
(11)
式中:k为迭代次数;Hs为海森矩阵;g为目标函数的梯度,其表达式为
(12)
式中J为雅可比矩阵。
忽略二阶导数和非对称项后,Hs简化为
(13)
反演过程中,反演迭代模型逐步收敛于真实模型,其目标函数拟合差RMS逐渐收敛于1.0,拟合差计算式为
(14)
式中:N为观测数据个数;F(m)为正演结果;δn为第n个数据的标准差。
2.3.3 正则化因子
本文采用Newman等[38]提出的方法计算正则化因子λ,其表达式为
|
(15)
式中:M为模型参数个数;am,j为矩阵(WdJ)T×(WdJ)中的元素。
3 激电效应对正演模拟结果的影响
3.1 一维模型
建立图2所示的一维海洋地电模型,在海底下方1km深度有一个厚度为100m的高阻油气储层,在离海底上方50m沿测线均匀布设51个水平电偶极源,间距为200m,所有水平电偶极源均平行于测线方向,接收点位于海底,即z=1000m深度位置。
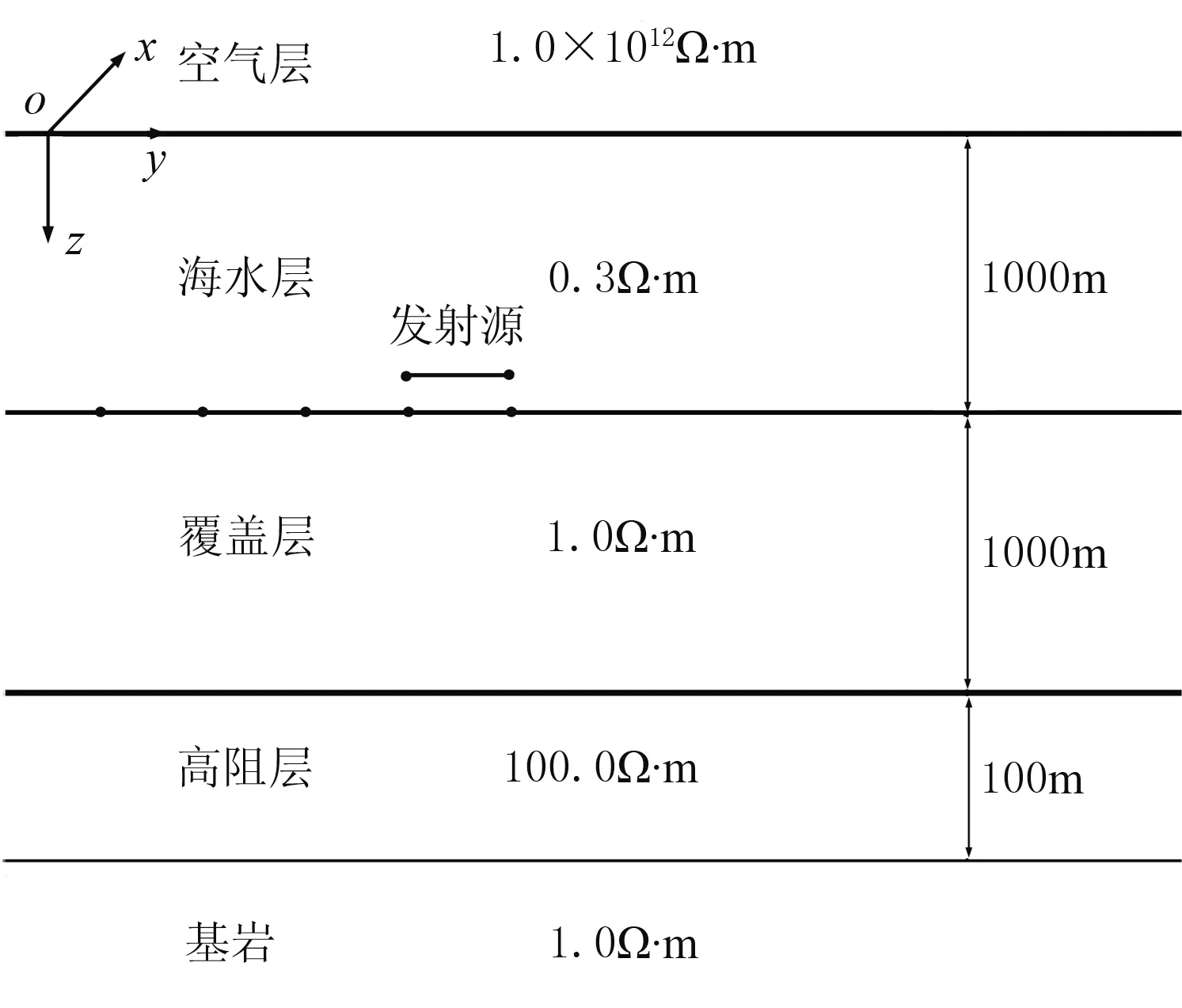
图2 一维海洋地电模型
基于MCSEM一维正演程序[29],分别计算了高阻模型(含高阻、非极化油气层)和极化模型(含高阻、极化油气层)的MCSEM响应。
3.1.1 激发频率的影响
为了讨论激发频率对MCSEM响应的影响,选择一组频率(范围为0.01~10Hz,在对数域均匀取100个频点),依次计算各个激发频率时高阻模型和极化模型的电磁场响应,再计算各频率时水平电场和水平磁场的IP强度。参照张春贺等[39]岩石样品物性测试结果,假定极化模型中η=0.1、0.3、0.5分别代表低极化率、中极化率和高极化率。
从图3可以看出,随着频率增大,水平电场和水平磁场的IP强度增大,高频时呈现“阶梯状”,且IP强度为零,其原因是绘图时删除了信号强度低于采集站本底噪声的数据。如果不删除这些数据,可能会得到与实际情况不符的非常大的值。
图4为收发距6000m处电场和磁场振幅随频率的变化曲线。由图可见,电场和磁场的振幅随着频率的增大而逐渐降低,而激电效应的影响随着频率的增大变得更加明显。
3.1.2 极化率的影响
为了讨论极化率对MCSEM响应的影响,选择一组极化率(范围为0~0.7,间隔为0.05),频率固定为0.25Hz,依次计算每个极化率下极化模型的电磁响应,再计算出各个极化率下的IP强度(图5)。
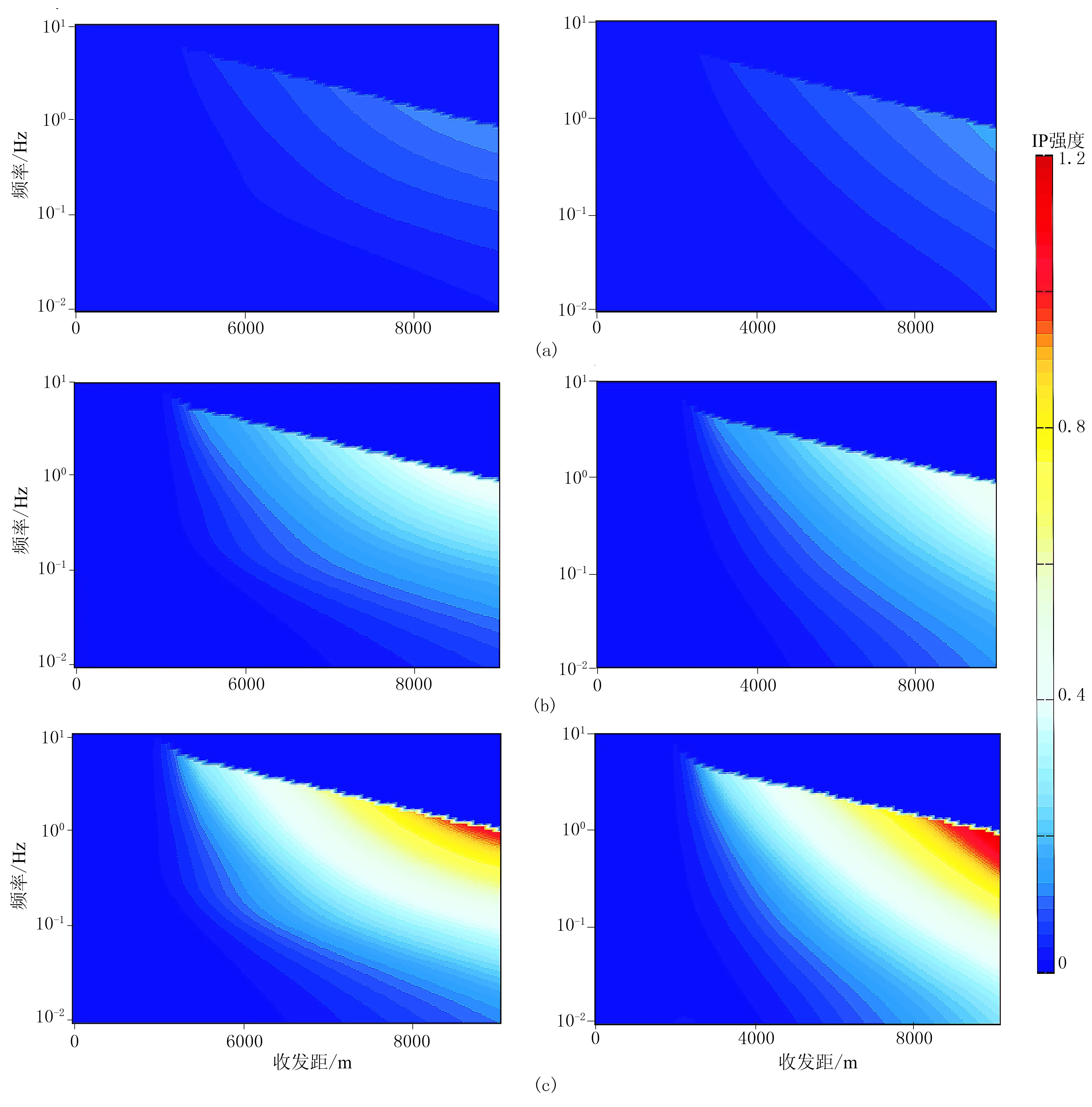
图3 不同极化率时水平电场(左)和水平磁场(右)IP强度随频率和收发距变化(a)η=0.1; (b)η=0.3; (c)η=0.5
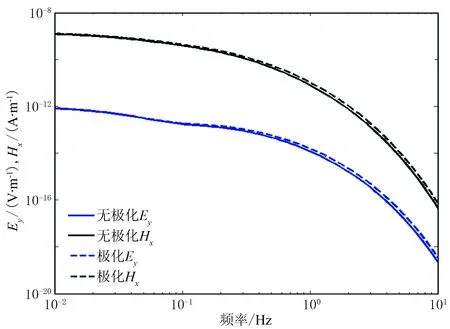
图4 收发距6000m处电、磁场振幅随频率的变化曲线
由图5可见,当极化率为一固定值时,IP强度随着收发距的增大而增大,这说明在大收发距处激电效应更强,这是因为位于大收发距处能够接收到来自地下更深处高阻层的电磁信号;当收发距为一固定值时,IP强度随着极化率的增大而增大。
3.1.3 上覆层和极化层厚度的影响
为了讨论覆盖层厚度和极化层厚度对MCSEM响应的影响,假定极化模型的极化率为中等极化率,即η=0.3,选择一组覆盖层厚度(200~1000m,间隔100m)和极化层厚度(20~200m,间隔20m),分别计算不同覆盖层厚度和极化层厚度情形下高阻模型和极化模型的电磁场响应,再分别计算水平电场和水平磁场的IP强度(图6、图7)。
由图6可见,覆盖层厚度变化对IP强度影响不大。由图7可见,当收发距达到一固定值(4000m)时,随着极化层厚度的增大,IP强度呈现减小的趋势。这是因为随着极化层厚度的增大,由极化层厚度增加产生的影响超过激电效应的影响而占据优势,从而导致激电效应的影响不能被凸显。
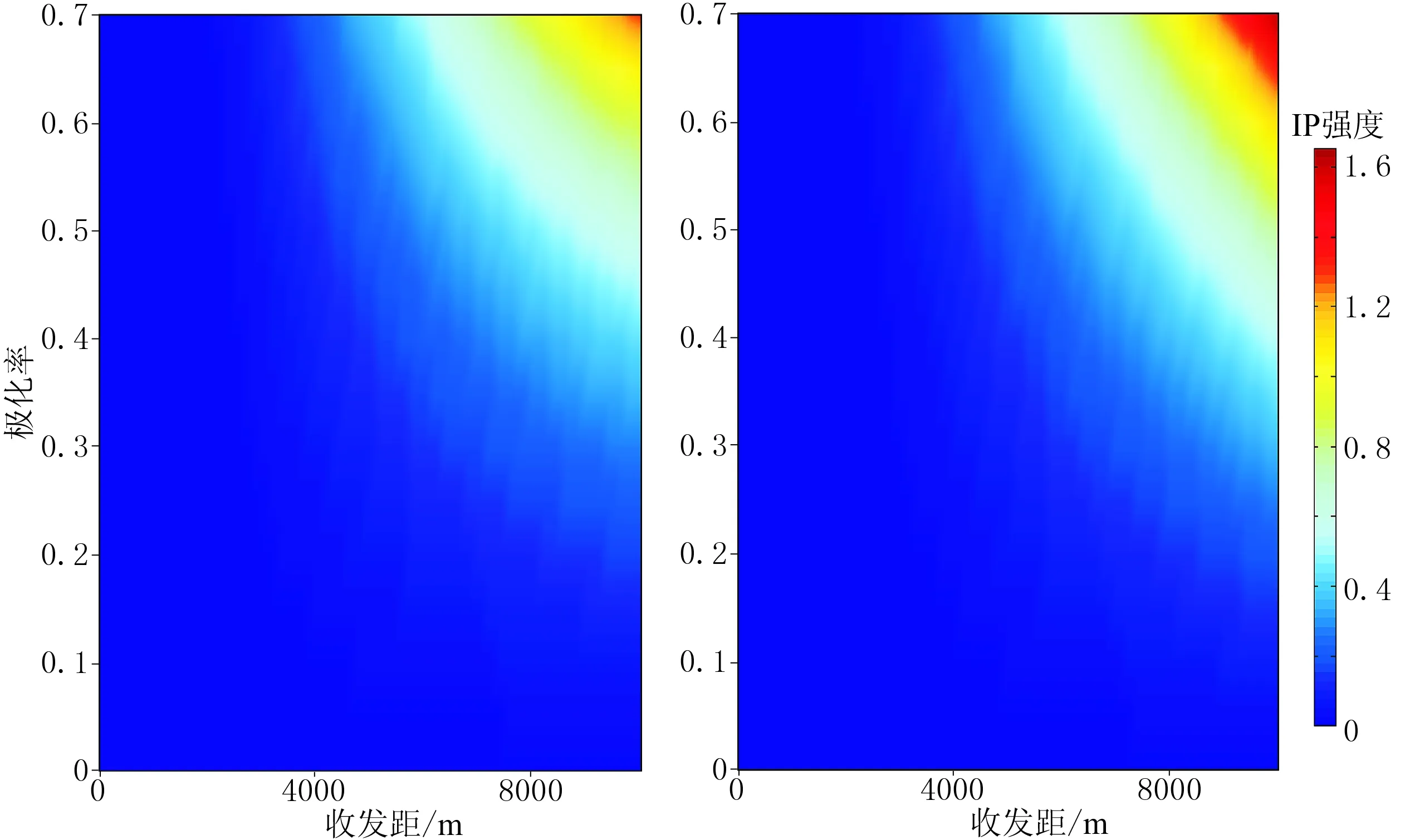
图5 水平电场(左)和水平磁场(右)的IP强度随极化率和收发距的变化
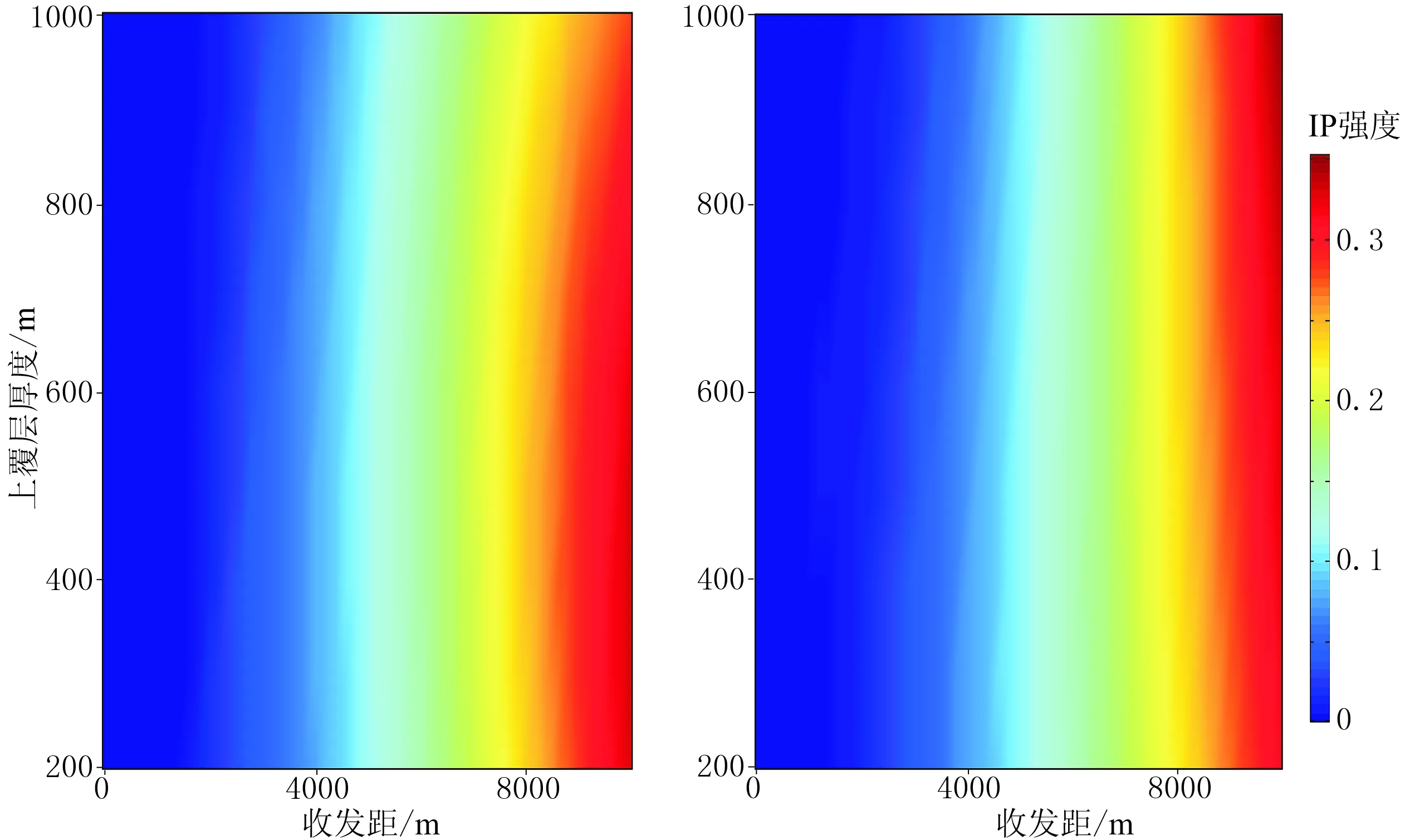
图6 水平电场(左)和水平磁场(右)的IP强度随上覆层厚度和收发距的变化

图7 水平电场(左)和水平磁场(右)的IP强度随极化层厚度和收发距的变化
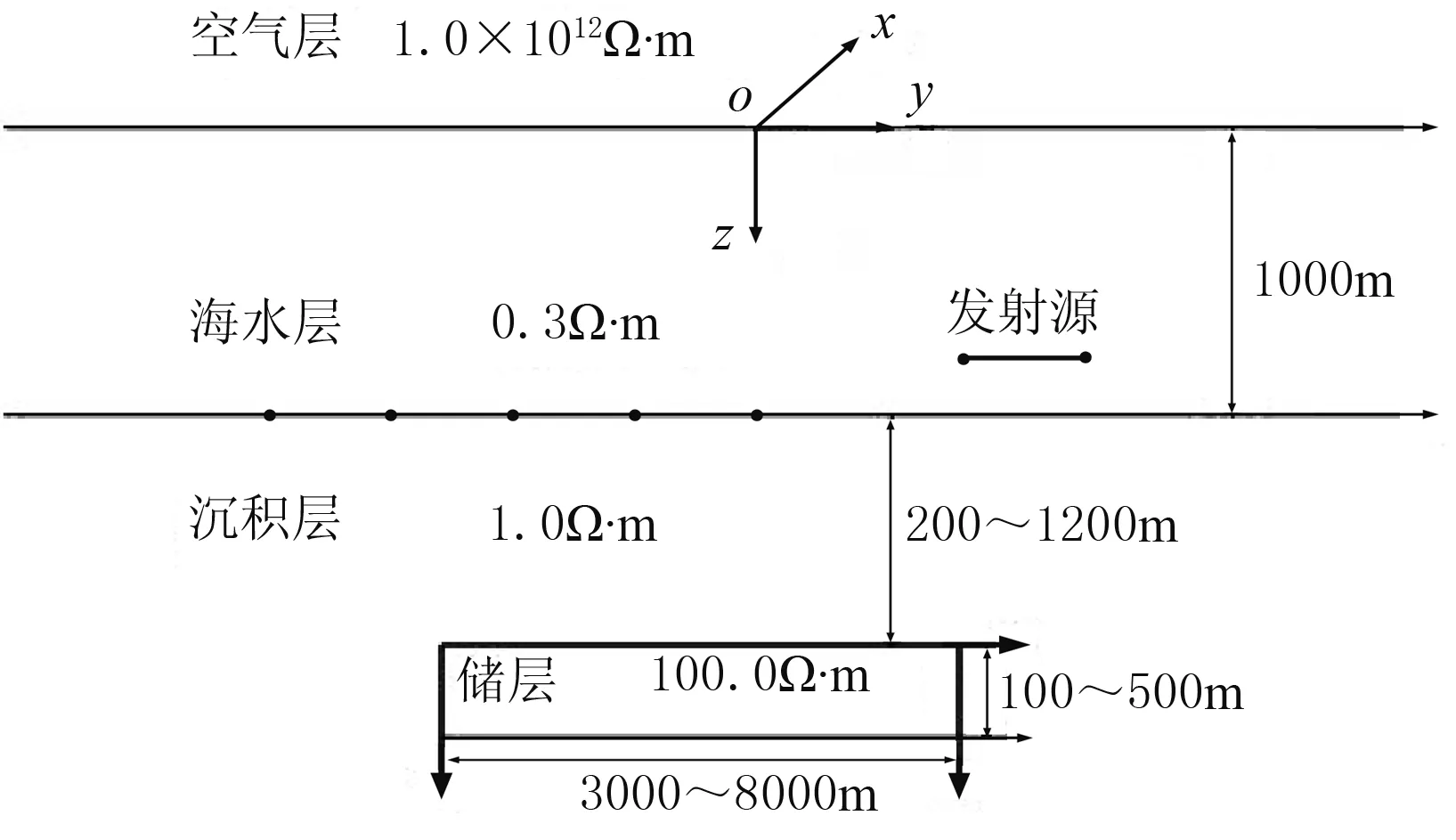
图8 二维模型示意图
3.2 二维模型
基于MCSEM二维有限差分程序[30]模拟并讨论激电效应对二维模型MCSEM响应的影响。二维模型如图8所示。水平电偶极源置于海底上方50m深度处,在海底布设51个接收站,接收站间距为200m。为了研究储层埋深、宽度及其厚度对IP强度的影响,假定储层埋深范围为200~1200m,宽度为3000~8000m,厚度范围为100~500m。在二维模型数值模拟中,极化率设定为中等数值(η=0.3),频率为0.25Hz。
图9为二维模型IP强度随极化层埋深和收发距变化关系。模拟计算时,二维极化层宽度和厚度固定,分别设定为6000m和100m,极化层埋深从200m变化到1200m。从图9可以看出,随着极化层埋深增大,IP强度呈现减小趋势,说明随着油气储层埋深变大,激电效应变弱。
图10为IP强度随极化层宽度和收发距变化关系。模拟计算时,二维极化层埋深和厚度固定,分别设为1000m和100m,极化层宽度从3000m变化到8000m。从图10可以看出,IP强度随着油气储层宽度的增大而增大,说明储层宽度越大,激电效应越强。
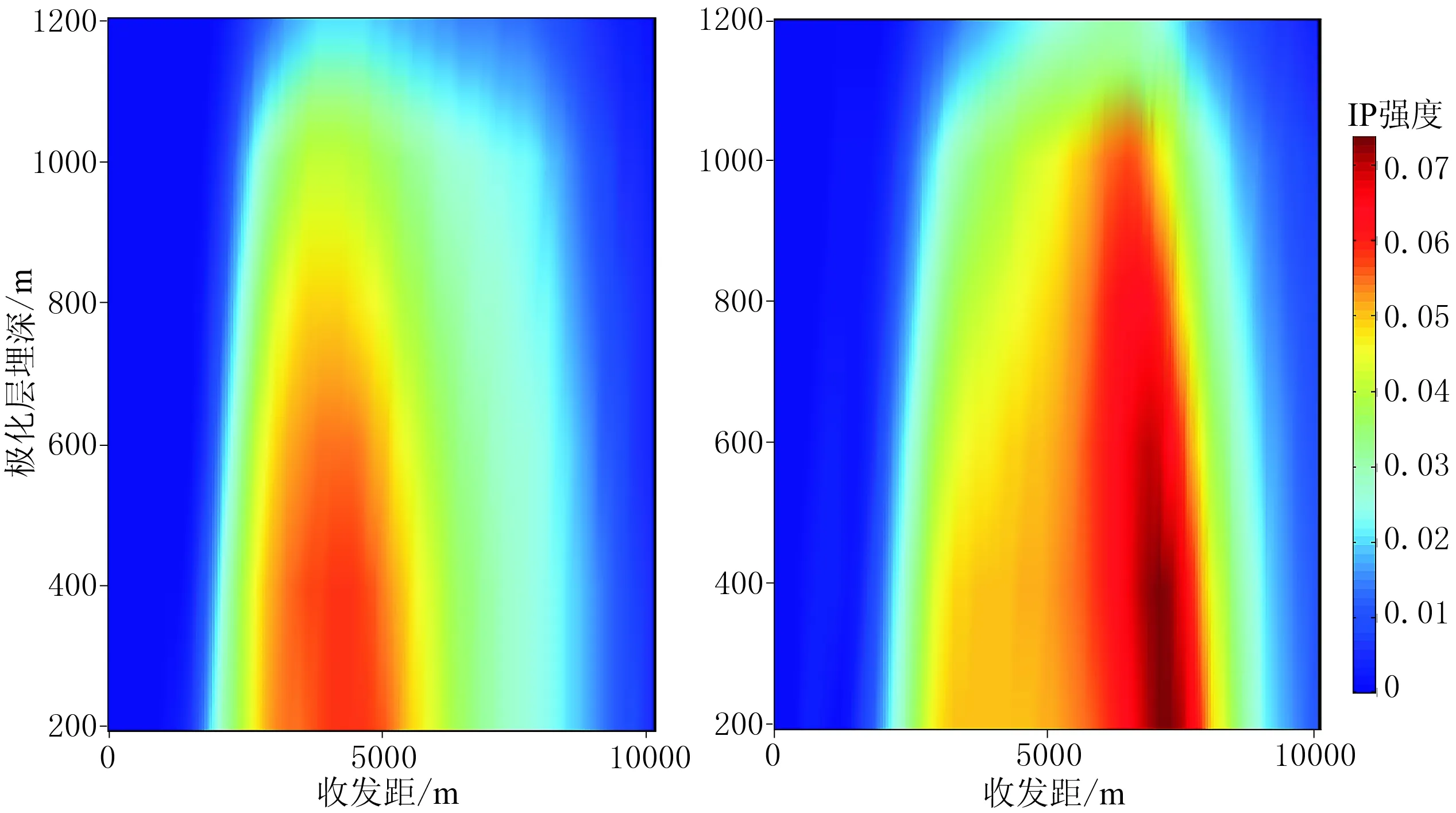
图9 水平电场(左)和水平磁场(右)的IP强度随极化层埋深和收发距的变化
图11为IP强度随极化层厚度和收发距变化关系。模拟计算时,二维极化层埋深和宽度固定,分别设为1000m和6000m,极化层厚度从100m变化到500m。从图11可以看出,随着储层厚度增大,IP强度呈现减小趋势。与一维模型计算结果类似,随着极化层厚度增大,由极化层厚度本身产生的影响逐渐超过激电效应的影响而占据优势,从而导致激电效应的影响不能被凸显。
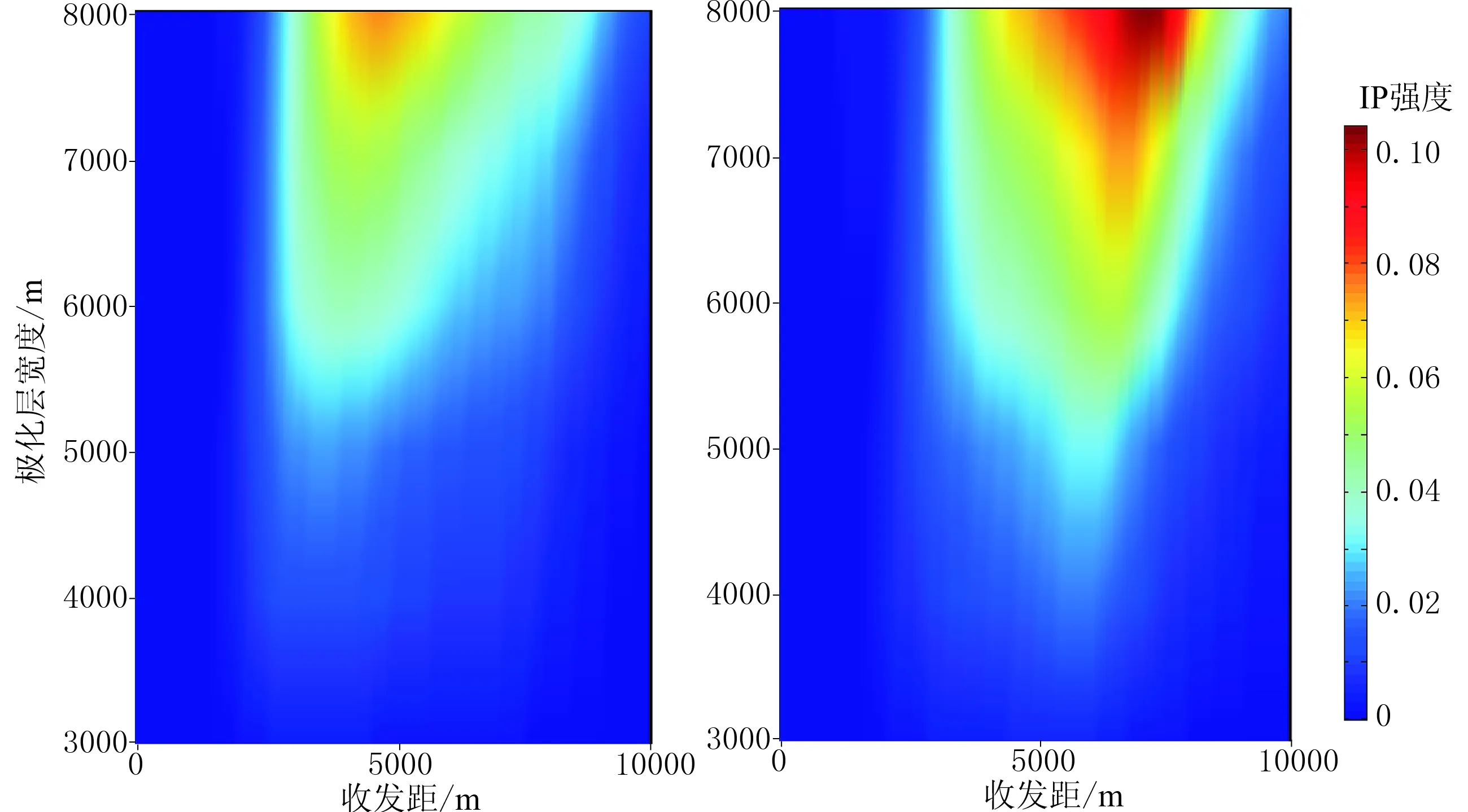
图10 水平电场(左)和水平磁场(右)的IP强度随极化层宽度和收发距的变化
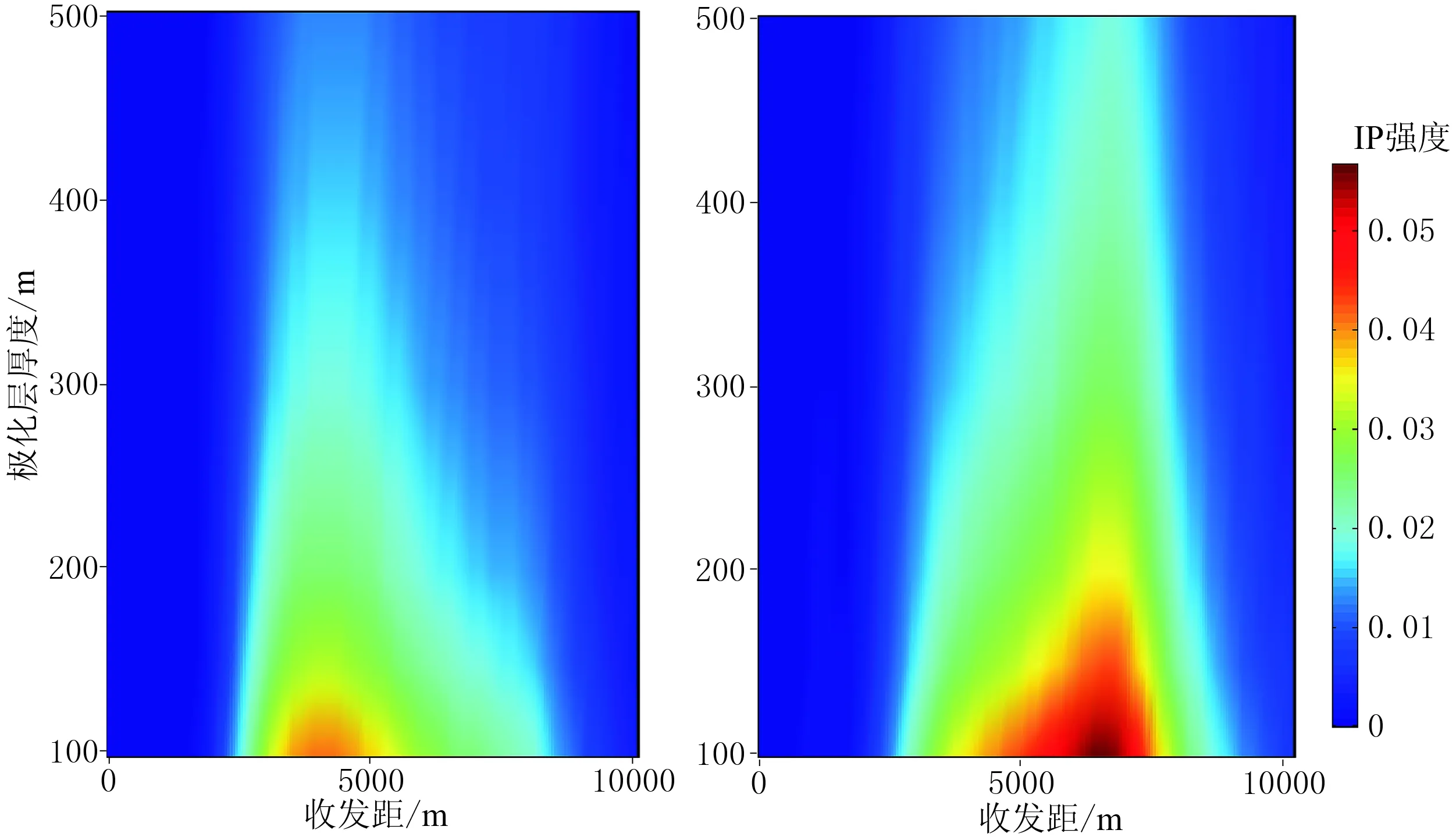
图11 水平电场(左)和水平磁场(右)的IP强度随极化层厚度和收发距的变化
4 激电效应对反演结果的影响
为研究激电效应对一维MCSEM反演结果的影响,本文在一维反演程序[35]的基础上做了修改,在反演过程中考虑了激电效应,即在反演时给定Cole-Cole模型中的三个参数(频率相关系数c、时间常数τ和极化率η),只反演电阻率ρ。对图2所示一维海洋地电模型进行反演。正演模拟时设定发射频率为0.1和1.0,极化率分别为0.1、0.3和0.5,时间常数为2.0,频率相关系数为0.25。反演时添加2%的随机噪声。
首先通过一维MCSEM正演程序,计算含有激电效应的MCSEM数据。然后将该正演数据分别使用考虑和不考虑激电效应的反演程序进行反演,最后对两个反演结果进行对比分析,讨论激电效应对反演结果的影响。
图12为极化率分别为0.1、0.3和0.5时的电阻率反演结果。由图可见,如果反演时不考虑激电效应,反演得到的电阻率比实际值偏大,并且电阻率随着极化率的增大而增大。通过对比两种情形下的电阻率反演结果可知,激电效应的存在除了使电阻率反演结果偏大一些之外,并未产生其他明显影响,即激电效应对一维反演结果的影响很小。
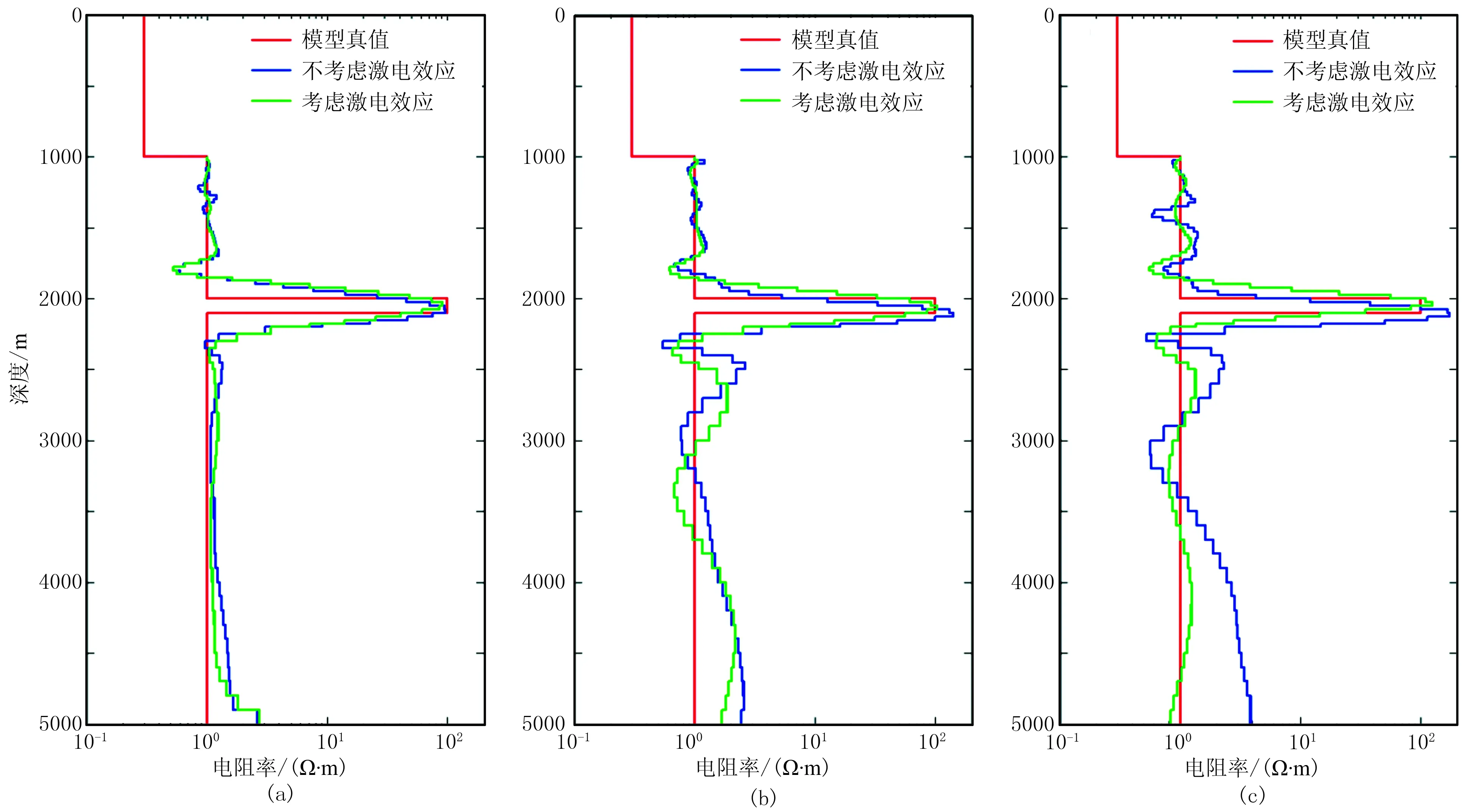
图12 不同极化率以及考虑、不考虑激电效应的电阻率反演结果对比(a)η=0.1; (b)η=0.3; (c)η=0.5
5 结论
本文通过引入Cole-Cole模型,对储层极化引起的激电效应进行了分析,定义了IP强度用以表示激电效应的强弱,研究了激电效应对MCSEM正演和反演结果的影响,得出以下几点认识:
(1)海底油气层极化产生的激电效应不仅与激电参数有关,而且与观测频率、极化层厚度、埋深、宽度等因素有关。对于一维层状介质,激电效应强度随着激电参数的增大而增大,激电效应强度随着极化层埋深和厚度的增大而减小;对于二维地电模型,激电效应强度随着极化层宽度增大而增大。
(2)激电效应对一维和二维地电模型MCSEM响应的影响特征类似。但是由于二维模型中储层宽度有限,所以其激电效应的影响程度明显小于一维情形。
(3)激电效应会对反演结果产生一定影响,如果不考虑激电效应,高阻储层的反演电阻率会偏大,但是差异并不十分明显。

