一种基于MTLS优化的非等间距多点灰色变形预测模型
甘祥前,任 超,刘林波,刘中流,杨 庆
(1. 桂林理工大学测绘地理信息学院,广西 桂林 541004; 2. 广西空间信息与测绘重点实验室,广西 桂林 541004)
变形预测常用的模型主要有传统灰色预测模型、时间序列分析、回归分析和神经网络等[1-4]。这些方法大多为单点建模与预测[5],而事实上监测工程建筑物的变形状态都布设有大量的变形监测点,监测点间是相互影响、彼此关联的,单点的处理没有利用监测点间相互关系的信息,不足以反映变形体的整体变形趋势和变形规律[6-9]。因此,在变形监测分析与预报中,使用多点灰色预测模型更为合理。但在实际工程中可能存在非等间距观测或某几期缺测的实际状况,对此,近年来不少学者对非等间距多点灰色变形预测模型进行了研究,其中文献[10]将单点变形分析扩展到空间多点的整体变形分析,采用非等间距等距化处理的改进方法,建立了非等间距多点变形预测模型;文献[11]在GIS平台下结合多变量非等间距灰色预测模型,开发了一套露天矿边坡灾害预警系统;文献[12]建立了多变量非等间距灰色模型并应用于中国农村青少年生长水平预测。目前,这些方法大多为对非等间距多点灰色模型进行等距化改进或对其背景值和残差项优化。但是在传统的非等间距多点灰色预测模型建模过程中,发展系数A和灰作用量B是在最小二乘(LS)约束准则下求解的,而LS在求解参数过程中只是对预测值进行改正,把已知的测量值当作是不含误差的,因此此时的LS估计就不再是无偏的[13]。为了解决这个问题,本文引入多元整体最小二乘法(MTLS),MTLS是由整体最小二乘法(TLS)拓展得到的,是将TLS中的参数向量和观测向量拓展为参数矩阵和观测矩阵,在计算过程中同时顾及观测值矩阵和系数矩阵存在的误差。
1 非等间距多点灰色变形预测模型
1.1 模型的建立
相关联的多个变形监测点的非等间距原始观测序列为
(1)
时间间隔ΔTk=Tk-Tk-1,其中i=1,2,…,m,m为变形监测点数目,将多个变形监测点的观测序列组成矩阵形式
X(0)(T)=[X(0)(T1)X(0)(T2)X(0)(T3)…
X(0)(Tj)…X(0)(Tn)]
(2)
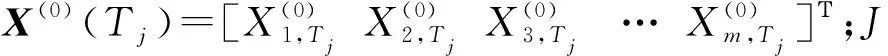
对式(2)进行累加生成X(1)(T),然后建立n元一阶常微分方程组,其矩阵形式为
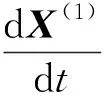
(3)
利用积分生成变换原理对式(3)进行整理得到响应函数式
X(1)(Tk)=eA(Tk-T1)X(1)(T1)-A-1(I-eA(Tk-T1))B
(4)
最后还原式(4)得到非等间距多点预测模型
(5)
式中,k=1,2,…,m。
1.2 模型精度检验
2 多元整体最小二乘及其解法
首先将该矩阵方程改写
(6)
(7)
式中,eY=vec(EY)为列向量化后的观测值的残差向量;eB=vec(EB)为列向量化后的系数矩阵的残差向量。
利用拉格朗日乘数法对MTLS进行求解,以式(6)为条件,构造拉格朗日目标函数
eY-[Ir⊗(B-EB)]ξ}
(8)
式中,λ为拉格朗日乘常数;⊗为克罗内克积算子。对式(8)求一阶偏导,令其等于0,联立方程求解,最后得到
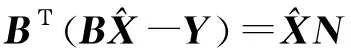
通过迭代,求出最终解,具体迭代步骤如下:
3 实例分析与验证
本文试验数据来源于文献[10],选取的是某基坑北侧边坡上相互关联的4个沉降监测点A、B、C、D的观测数据,并对其进行了整体变形分析与建模。试验以该4个沉降监测点的13期观测数据作为样本进行模型的分析与验证。
3.1 建模数据为9和建模数据为10的模型预测效果比较
根据本文给出的建模理论,首先分别建立建模数据为9和10的非等间距多点灰色变形预测模型,然后对这两种模型的预测效果进行比较,分析两种不同建模数据情况下对非等间距多点灰色模型预测精度的影响。
通过计算,得到两种不同建模数据下的模型拟合及预测值、预测值平均相对误差、拟合精度及残差结果见表1和表2。
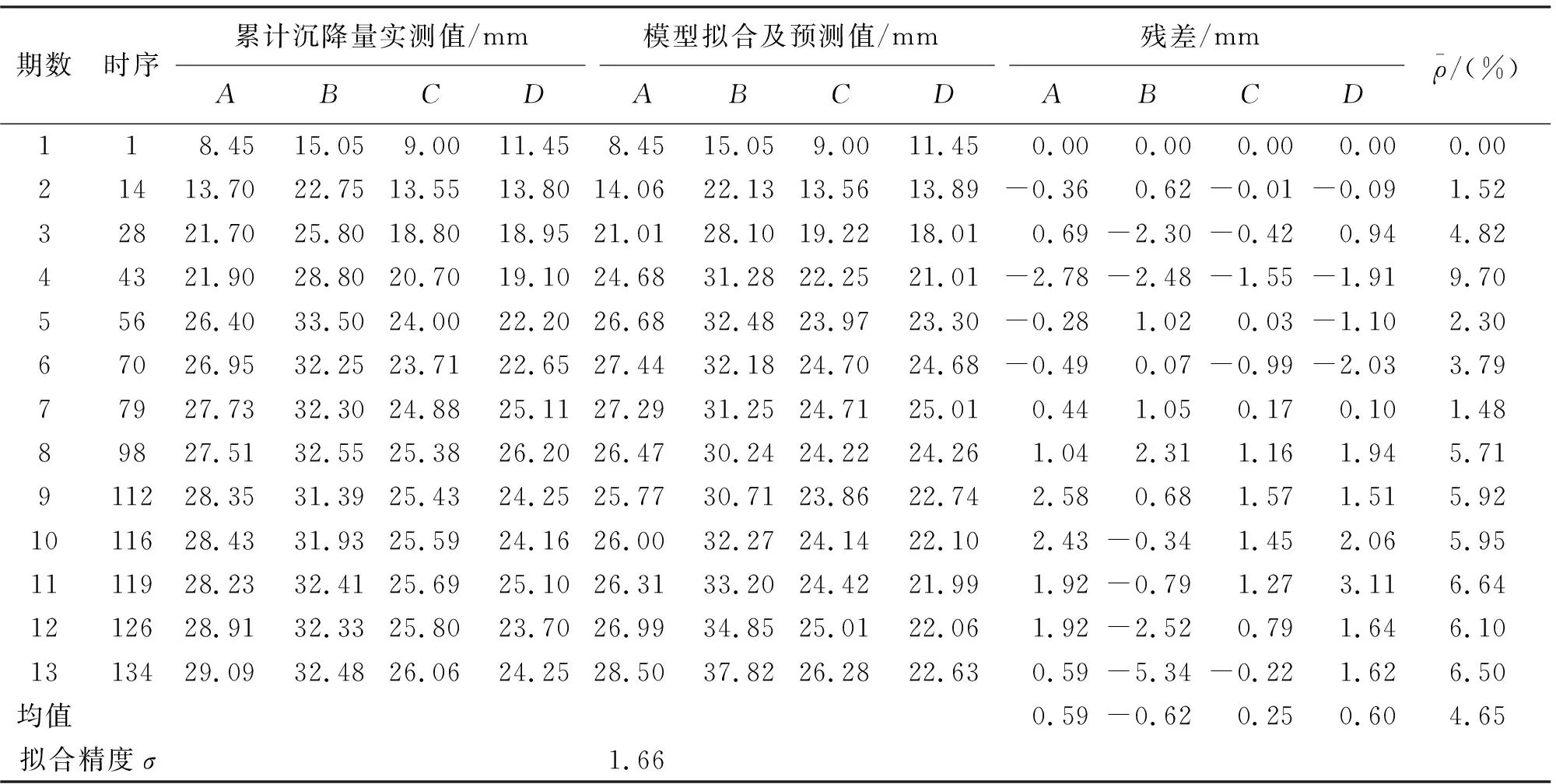
表1 建模数据为9的模型拟合及预测结果
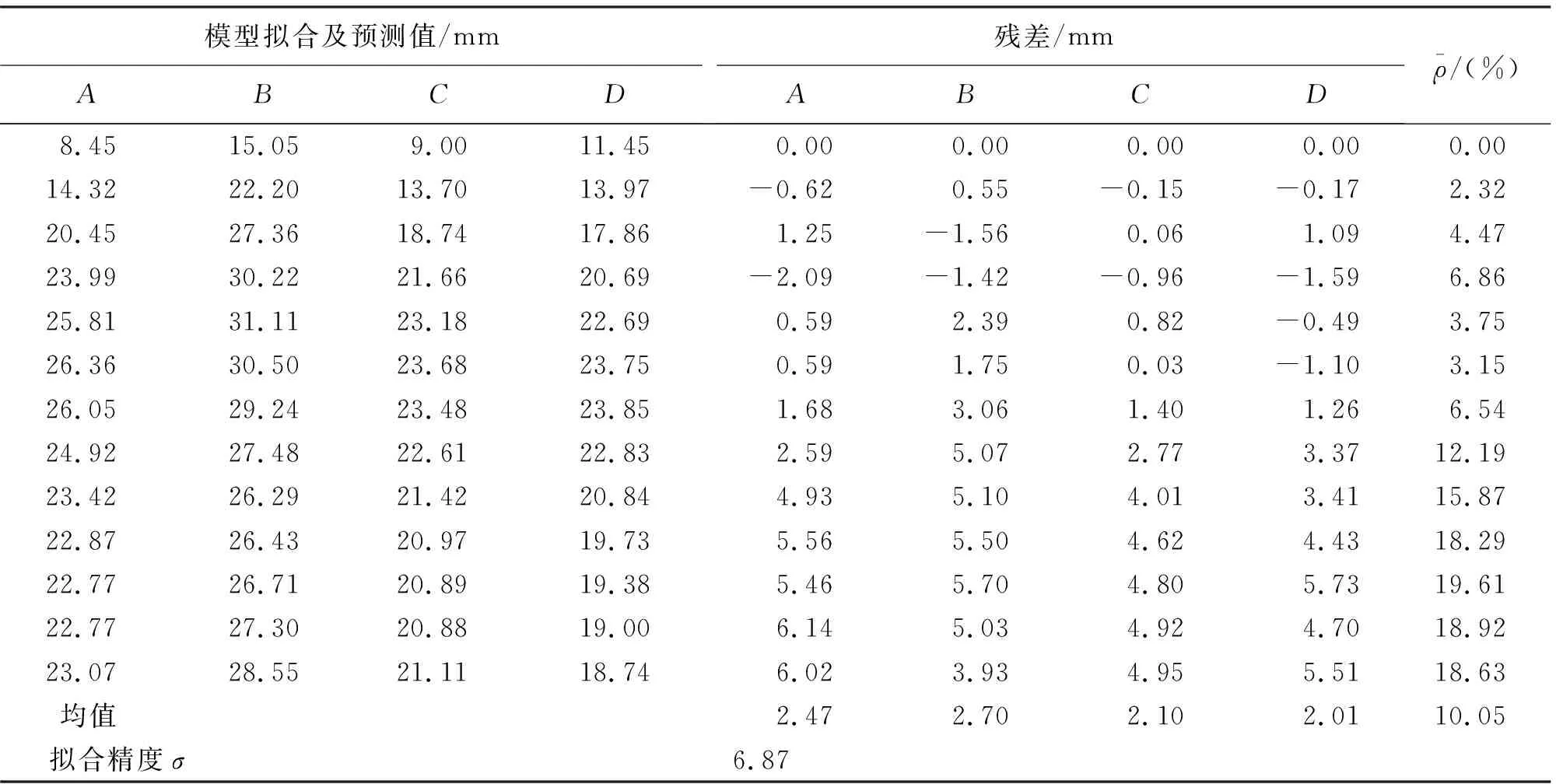
表2 建模数据为10的模型拟合及预测结果
通过对表1,表2计算结果的对比分析发现,建模数据为9的模型拟合精度、预测精度、残差均值都远远优于建模数据为10的,说明把第10期观测数据纳入建模数据后,模型受到了较大的扰动,即新增的建模数据中含有较大误差,再加上模型的分析是整体性的,因此个别带有误差数据的引入有可能对模型的预测精度造成很大的影响。针对这个问题,下节给出MTLS优化非等间距多点灰色预测模型的算法。
3.2 MTLS优化的非等间距多点灰色变形预测模型算例
试验引入MTLS对建模数据为10的模型进行优化,建立MTLS优化的非等间距多点灰色变形预测模型。
根据多元整体最小二乘理论,计算得到MTLS优化模型的拟合及预测值、预测值平均相对误差、拟合精度及残差结果见表3。
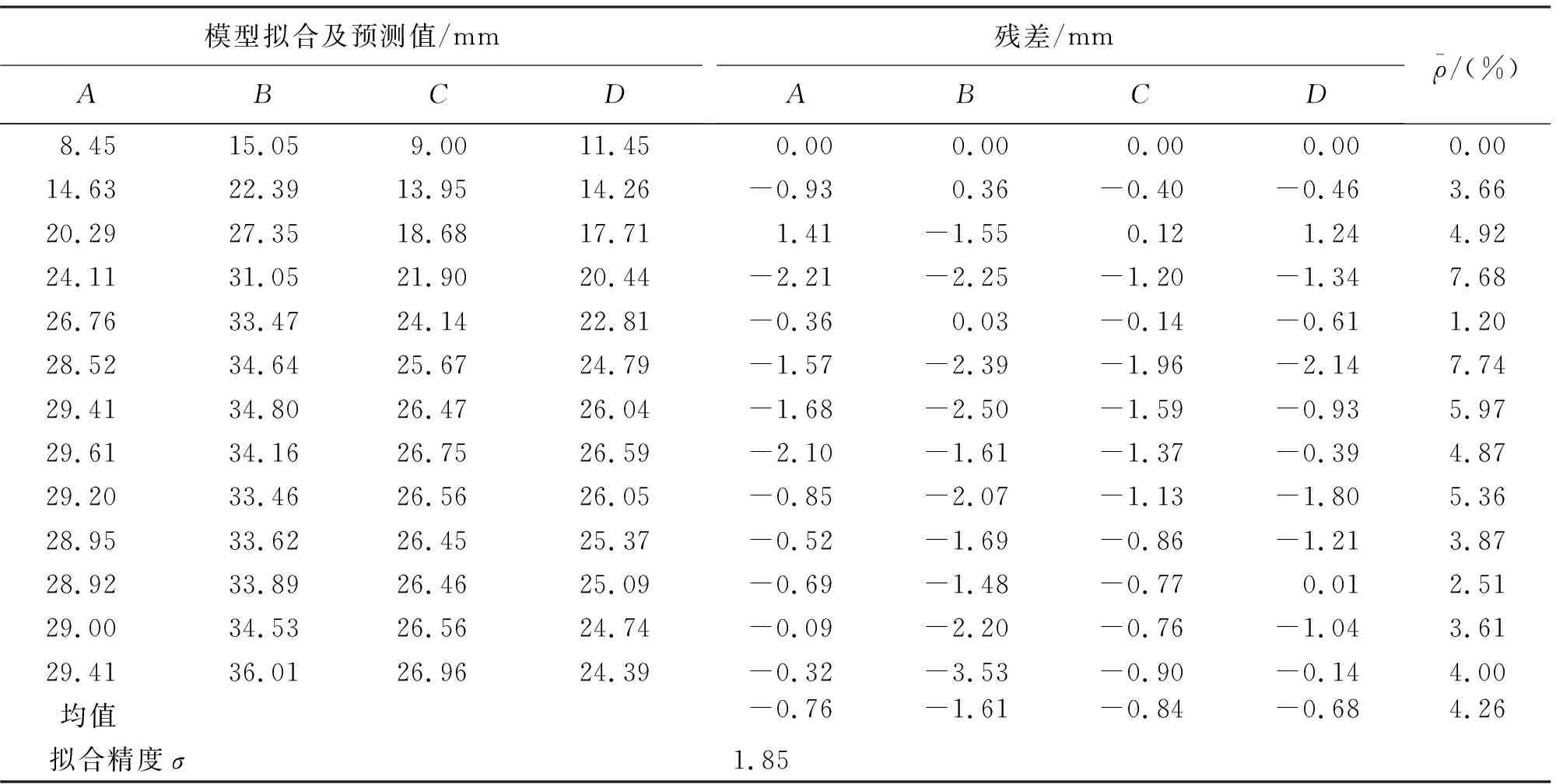
表3 基于MTLS的非等间距多点灰色预测模型的拟合及预测结果
3.3 不同模型预测结果对比与分析
对表1、表2和表3中的计算结果进行对比分析,得出不同模型的预测结果精度对比见表4。
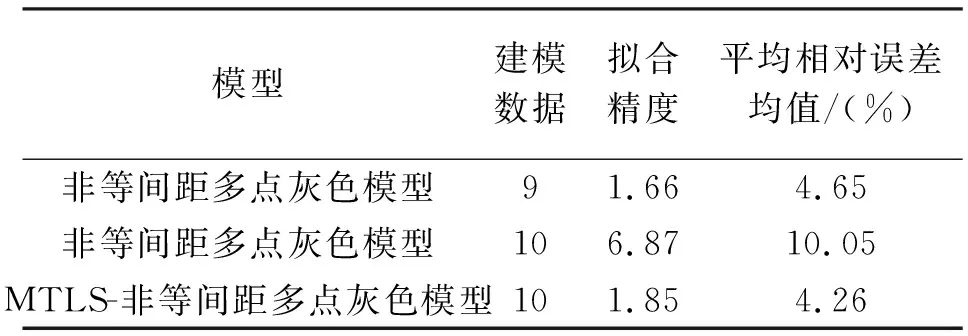
表4 不同模型的预测结果精度对比
为了更清晰地比较不同模型的预测效果,把实测值和预测值绘制成曲线,如图1所示。
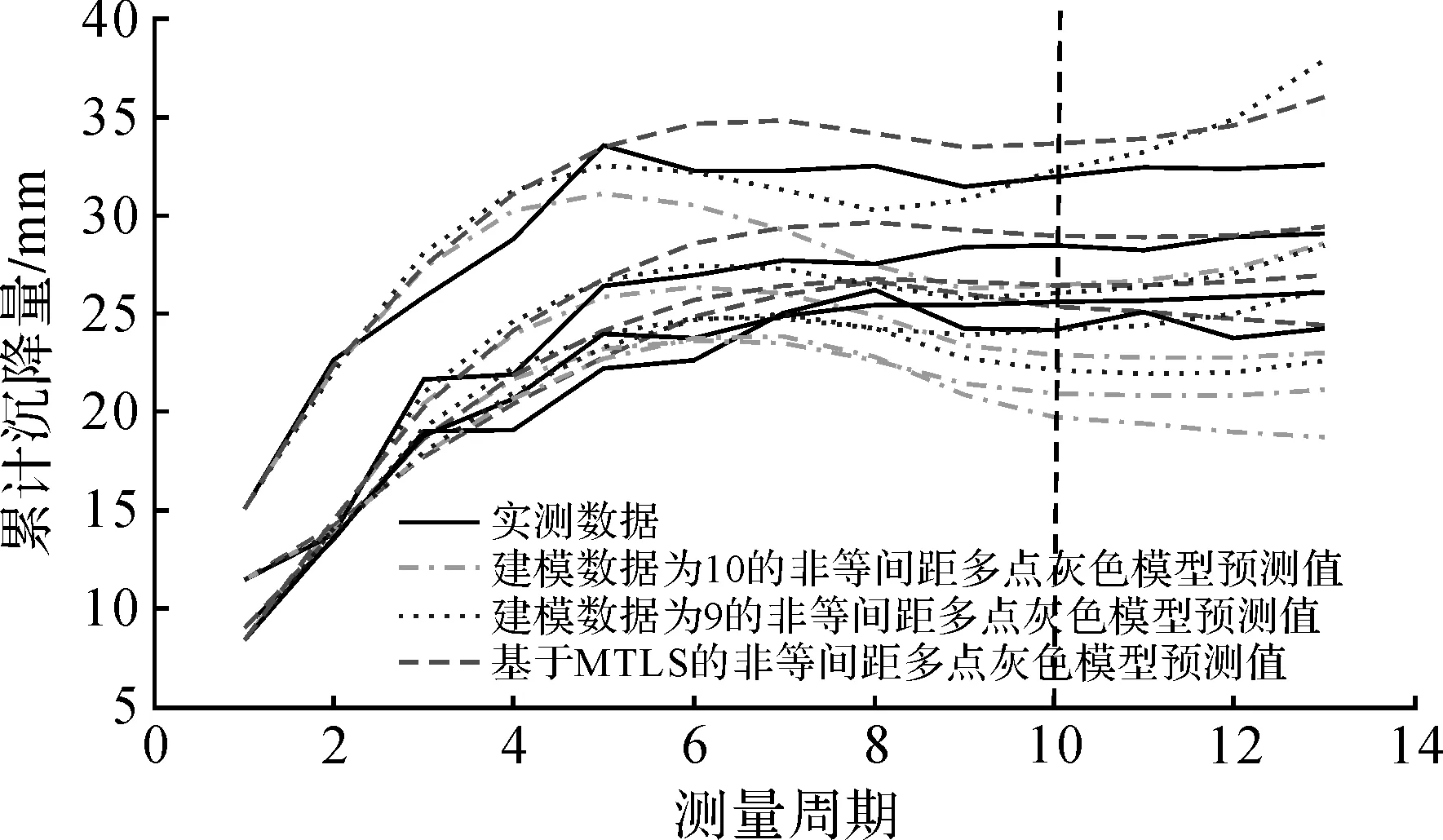
图1 不同模型预测效果对比
由表4可知,对于扰动性较大的非等间距多点灰色预测模型,经MTLS优化后模型拟合精度达到1.85,预测值平均相对误差均值达到4.26%,相比优化前,其模型精度得到了很大提高。通过与建模数据为9的模型对比,MTLS优化后模型的拟合精度虽然低了些,但其预测精度更高。此外通过图1也可以清晰地看出MTLS优化模型的预测曲线较另外两种模型更接近于实测曲线。说明多元整体最小二乘法对建模数据误差起到了很好的抑制效果,并且提高了非等间距多点灰色预测模型的拟合及预测精度,基于该方法优化的模型稳定性更好。
4 结 语
本文在传统非等间距多点灰色预测模型的基础上,结合实际工程中多个相关联沉降监测点的变形观测数据。首先分别在建模数据为9和10的情况下,建立非等间距多点灰色预测模型,通过对两者预测效果的对比,发现建模数据为10时,模型的扰动性较大,建模数据存在较大误差;然后针对这一缺陷,本文提出了用MTLS代替传统的LS对非等间距多点灰色预测模型中的发展系数A和灰作用量B进行求解。最后通过实例分析验证,该方法可以有效地抑制建模数据误差,提高非等间距多点灰色预测模型的拟合及预测精度,适合在变形预测中应用。
虽然本文对改进非等间距多点灰色预测模型的研究取得了一定的成果,但也存在不足之处。文中只与多点非等间距灰色预测模型作对比,而没有与单点非等间距灰色模型比较,基于整体最小二乘优化的单点非等间距灰色模型预测精度是否更好,本文并没有给出证实,这有待于进一步研究。

