地形熵聚类下利用多面函数拟合高程异常
孙佳龙,郭淑艳,龙冰心,秦思远
(1. 淮海工学院测绘与海洋信息学院,江苏 连云港 222005; 2. 海岛(礁)测绘技术国家测绘地理信息局重点实验室,山东 青岛 266590; 3. 海岸带地理环境监测国家测绘地理信息局重点实验室,广东 深圳 518060; 4. 江苏省海洋资源开发研究院,江苏 连云港 222001; 5. 北京大地宏图勘测科技有限公司,北京 100029)
高程异常是似大地水准面与参考椭球面之间的高程差值。在一个区域内精确确定高程异常,就可以通过GPS观测的大地高准确地求出正常高,从而减少对水准测量工作的依赖,提高测量效率[1-3]。在一个区域内确定高程异常,通常是利用已知点的高程异常拟合高程异常曲面,从而插值得出待定点的高程异常。高程异常曲面的拟合方法主要有多项式拟合法、二次曲面拟合法和多面函数拟合法等[4-6]。多面函数法是从几何观点出发,解决根据数据点所形成的平差数学曲面问题,该方法主要应用于拟合重力异常、大地水准面差距、垂线偏差等。而在多面函数拟合时,首先需要确定中心点,中心点选择的不同,在很大程度上决定了最后的拟合精度[7]。人为选择中心点,会导致拟合的精度随经验的变化而不同,从而导致求解的高程异常值因人而异。聚类分析方法可以利用点与点之间的空间距离进行分类,从而在分类结果中有效地选择出中心点,但利用该方法需首先确定分类的个数,而分类个数有时又难以确定[8-9]。本文以地形熵作为一个参考量,首先确定分类个数,然后以点与点之间的空间距离与地形熵的比值作为指标,从众多高程异常点中选择多面函数的中心点,并利用多面函数进行拟合,同时与其他方法进行比较,以期得出一些有益的结论。
1 多面函数
多面函数的理论依据为:任意数学表面与任意不规则的圆滑表面,总可以利用一系列有规则的数学表面总和,以任意精度逼近。因此,由多面函数表示的残差高程异常为[4]
(1)
式中,aj为待定系数;Q(x,y,xj,yj)为x和y的二次函数,其中心点在(xj,yj)处;n为中心点的个数;ζ可由二次式的和确定,故称多面函数。
用一组简单的解析函数的线性组合对这个曲面进行逼近,通常选择多元二次函数作为解析函数,其形式为[6]
(2)
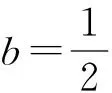
将式(2)写成误差方程,并用矩阵表示为
V=QA-ζ
(3)
待定系数A可根据已知GPS/水准数据和地球重力场模型得到的残差高程异常,按最小二乘法计算[10-11]
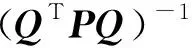
(4)
由此可根据系数A和式(1)求解其他点的残差高程异常。
2 地形熵聚类多面函数拟合方法
当用多面函数表示残差高程异常时,由于选择的中心点个数n要小于已知的高程异常值的个数,因此,需要对所有的高程异常值进行选取。人为选取高程异常值既耗时又费力,且容易出错。利用聚类分析方法选择中心点时,需要首先确定分类个数,而对于某一区域的高程异常而言,分类个数有时难以确定。作为一种表示地形复杂程度的指标,地形熵可以较准确地表示局部区域高程值变化的剧烈程度[12-15]。地形熵定义为
(5)
式中,h(i,j)为高程,在本文中,以高程异常值代替高程。局部地形熵反映了地形所含有信息量的大小,因此,局部地形熵可以描述地形的性质。局部区域高程值变化越急剧,起伏变化越大,地形越独特,则计算出的局部地形熵越小,否则熵就越大。高程异常值变化越剧烈的位置,该点应参与到曲面拟合中,即应作为中心点,拟合多面函数。基于地形熵聚类的多面函数拟合算法过程如下:
(1) 将相邻两个高程异常数据点组成新块;
(2) 分别计算每块区域的地形熵;
(3) 如某块熵的相邻两块区域的熵均大于该块的熵,则该块熵为极小熵;
(4) 极小熵的个数n即为聚类分析的分类数,利用聚类分析算法对高程异常点进行聚类;
(5) 聚类分析中各类别的距离与各块区域地形熵的比值作为新的指标量,进行排序;
(6) 选择指标量最大的n个点作为多面函数的中心点,其余点为检核点。
3 实例解算与分析
某地区D级GPS控制网布设了18个观测点,对其进行了GPS观测和三等水准测量,利用GPS获得的大地高和水准测量得到的正常高,得到18个GPS/水准点的高程异常。各点的相对位置及高程异常值大小如图1所示。
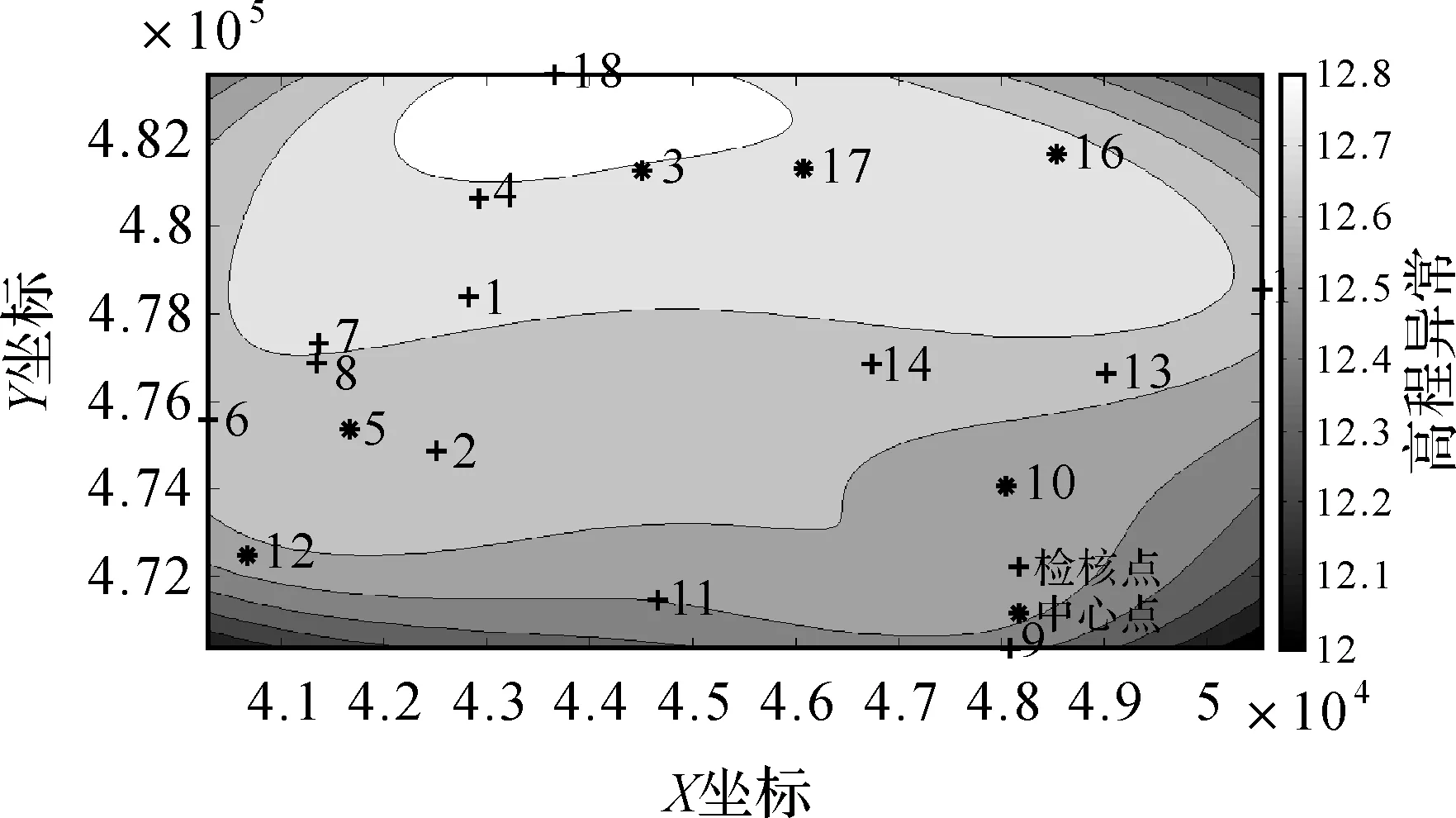
图1 高程异常点分布情况
从图1可以看出,这些点分布不均匀,在中间区域分布较少,在高程异常值较小的区域,点位个数也偏少。对这18个点的高程异常进行分块计算地形熵,如图2所示。
从图2可以看出,第2、6、9、12、15和17块区域为极小熵,与极小熵相邻较小的块熵为第3、5、10、11和16,由此可以得到重合的点号分别为3、6、10、12、16和17号点,共6个点。将聚类分析的分类个数取为6,进行聚类分析,结果如图3所示。
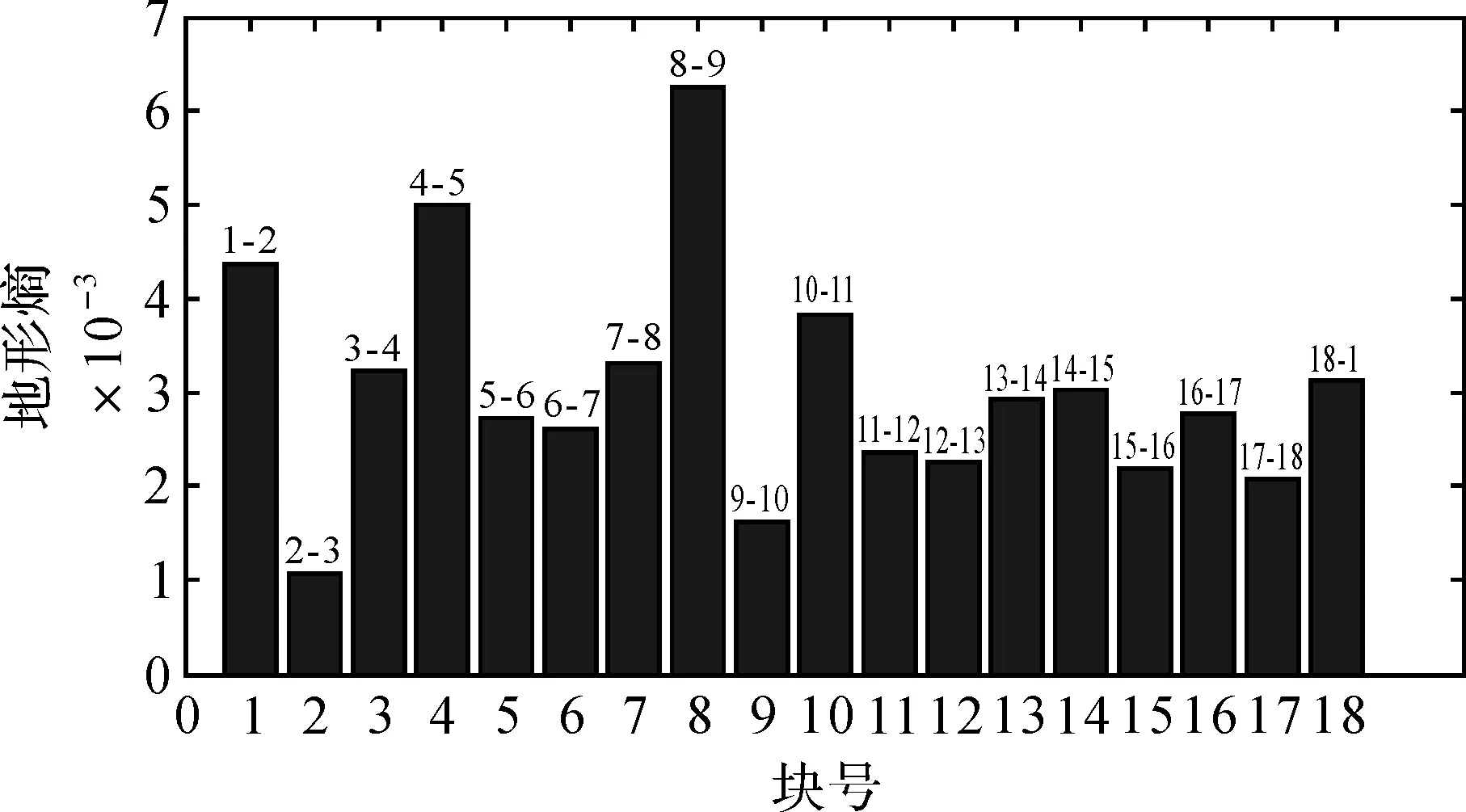
图2 各块区域地形熵
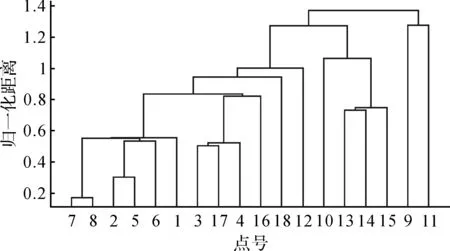
图3 聚类分析结果
从分类结果可以看出,距离比较近的点被分为一类,如7和8号点。由于9和11号点距离其他点均较远,因此也被分为一类。通过聚类分析,可以较好地将各点根据空间距离的远近分成不同的类。通过聚类分析,将距离最大的6个点,即9、10、11、12、16、18作为聚类分析选择的中心点。
无论是单独采用地形熵还是聚类分析,两者选择的点是有差异的。本文将空间距离与地形熵的比值作为新的指标量,既考虑了点与点之间的平面距离,又反映了高程异常值的变化情况,通过该指标,地形熵聚类法重新选择了中心点。利用不同方法选择的中心点进行了多面函数的拟合,求得检核点的高程异常,与检核点的实际高程异常求差,结果如图4所示。
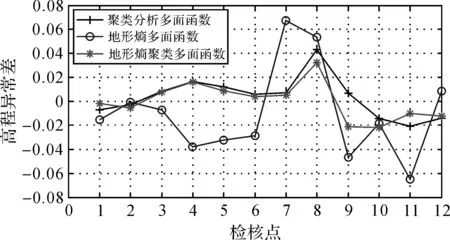
图4 多种方法选择中心点后的拟合结果
从图4可以看出,地形熵多面函数拟合的结果与实际高程异常值相比,在不同点差异较大,差异最小时接近0,而差异最大时超过0.06 m,说明地形熵多面函数在局部区域可以很好地选择中心点,实现有效拟合,但在个别区域差值较大。而聚类分析多面函数比地形熵多面函数变化幅度小,个别点高程异常差大于0.04 m,说明聚类分析多面函数在个别点与实际高程异常的差异也较大。而地形熵聚类的多面函数变化的幅度相对最小,最大差异值为0.03 m,为3种方法中最小的。3种方法的标准差和外符合精度见表1。

表1 拟合结果残差比较
从表1可以看出,10、12和16号点在3种方法中都被选择,说明这3个点具有很强的代表性。而3种方法选择的其他中心点却有所不同,说明采用不同的指标量得到的结果具有差异性。计算不同中心点的多面函数所拟合的高程异常,然后求其与实际高程异常的差值见表1,由地形熵多面函数拟合的结果在3种方法中无论是标准差还是外符合精度都是最低的,说明单独采用地形熵选择的中心点还不能很好地反映整个区域的高程异常变化,特别是随坐标的变化。而聚类分析得到精度较高,说明在高程异常变化不大的情况下,以空间距离的大小作为指标量,可以很好地获取中心点,从而提高拟合精度。当将地形熵和聚类分析方法结合后,得到的标准差和外符合精度都是最小的,说明同时考虑坐标和高程异常的变化可以在一定程度上提高曲面拟合精度,在外符合精度上分别比聚类分析和地形熵提高了28%和48%,说明了该方法的有效性。
4 结 语
利用地形熵可以较好地表征区域高程异常变化情况,从而为聚类分析提供分类个数。通过计算空间距离与地形熵的比值可以较好地反映整个区域的平面和高程异常变化整体情况。通过3种方法选择了多面函数的中心点,利用多面函数对整个区域的高程异常进行拟合,拟合结果显示距离与地形熵的比值是一个可以综合反映高程异常随空间位置变化的指标量,利用其选择的中心点并进行多面函数拟合的精度也最高,然而这个指标量对于一些特殊的区域是否适合还需进一步研究。

